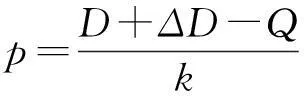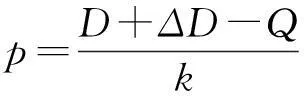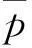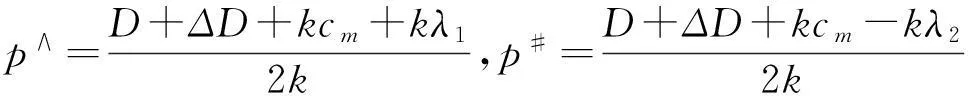销售市场和回收市场同时扰动下的闭环供应链协调应对

销售市场和回收市场同时扰动下的闭环供应链协调应对

覃艳华

(电子科技大学中山学院管理学院，广东中山528402)

摘要：考虑一个闭环供应链由单个制造商和单个零售商组成，产品的制造和再制造由制造商负责，产品的销售和废旧品的回收由零售商负责。在建立博弈模型的基础上，首先分析了闭环供应链在收益共享契约下的协调性，接着分析了收益共享契约对突发事件下闭环供应链的协调应对。分析结果表明：当突发事件导致销售市场规模和废旧品回收市场初始规模同时发生变化时，闭环供应链的协调将被打破，为此对收益共享契约进行了调整，调整后的收益共享契约使闭环供应链具有抗突发事件性；最后，通过数值计算实例对此进行了验证分析。

关键词：供应链管理；闭环供应链；突发事件；收益共享契约；协调

收稿日期：2014-03-13

基金项目：电子科技大学中山学院科研团队培育

作者简介：覃艳华(1972-)，女，苗族，广西河池人。副教授，硕士，研究方向为供应链管理、战略管理。

中图分类号：F272.3文章标识码：A

Closed-loop Supply Chain Coordination Under Selling Market

and Recycling Market Disruptions

QIN Yan-hua

(ManagementSchool,ZhongShanCollege,UniversityofElectronicScienceandTechnology,Zhongshan528402,China)

Abstract:A closed loop supply chain consisting of a single manufacturer and a single retailer is considered, the manufacturer is responsible for manufacturing and remanufacturing, the retailer is responsible for product sales and collection of waste products, the corresponding game model is established, and the coordination with revenue sharing contract is analyzed firstly. Then, the coordination with revenue sharing contract under emergency is studied. The results point out that the coordination of closed loop supply chain would be broken when the sale market size and the initial collection market size of waste products change simultaneity under emergency, so the revenue sharing contract is adjusted, the closed-loop supply chain has anti-emergency when the revenue sharing contract is adjusted. Finally, a numerical calculation example is given to verify the conclusion.

Key words:supply chain management; closed-loop supply chain; emergency; revenue sharing contract ; coordination

0引言

应急管理首先由Clausen等[1]提出，并在航空领域得到了很好的应用[2,3]，随后将其应用扩展到供应链等相关领域。Qi等[4]针对随机市场且需求与价格具有相关性的情况下，研究了突发事件引起需求扰动时的供应链协调问题；Xu等[5]研究了线性价格需求关系下需求扰动时的供应链协调应对问题；Huang等[6]研究了如何运用收益共享契约来实现供应链应对突发事件；胡劲松等[7]将二级供应链延伸到三级供应链，探讨了在收益共享契约下三级供应链如何应对突发事件；Xiao等[8]研究了两个具有竞争性的零售商组成的供应链系统在生产成本扰动时如何应对突发事件；王传涛等[9]研究了生产成本和市场需求扰动下的供应链协调应对；盛方正等[10]针对一个二级供应链系统，突发事件导致上游供应商不能满足零售商的需求，且零售商单位时间的订单拖欠成本是信息不对称时，指出可通过转移支付可实现供应链协调应对。但这些文献主要是针对正向供应链在突发事件下的协调研究，对闭环供应链如何协调应对突发事件并没有进行相应的研究。

随着环境保护和社会经济可持续发展双重压力的加剧，闭环供应链研究成为近几年来研究的热点[11,12]。目前关于闭环供应链如何应对突发事件的文献并不多见，牟宗玉等[13]研究了突发事件造成零售商的需求市场发生变化时如何运用两部收费契约来实现闭环供应链的协调应对；吴忠和等[14]针对随机市场需求且零售商销售成本信息不对称的情形，研究了突发事件造成市场需求和生产成本变化时的闭环供应链协调应对问题；李新然等[15]研究了第三方回收的闭环供应链协调应对突发事件问题；王玉燕[16]研究了销售市场需求和生产成本同时扰动的闭环供应链协调机制设计。但上述文献主要针对突发事件导致零售商面临的需求市场变化的情形来研究闭环供应链的协调应对问题，并没有考虑突发事件导致需求市场和回收市场同时变化的情况。

本文考虑突发事件导致闭环供应链销售市场规模和废旧品回收市场初始规模同时变化的情形，指出在正常情况下基准的收益共享契约能够实现闭环供应链的协调，但当销售市场规模和废旧品回收市场初始规模在突发事件下同时变化时，闭环供应链协调在原有的收益共享契约下将失效，为此闭环供应链可通过调整收益共享契约能够协调应对突发事件。

1闭环供应链基准的收益共享模型分析

考虑一个二级闭环供应链，它是由单个制造商和单个零售商组成的，产品的制造和再制造由制造商负责，产品的销售和废旧品的回收由零售商负责。设使用原材料生产新产品时制造商的单位产品成本为cm，使用废旧品进行再制造时制造商的单位产品成本为cr(cm>cr>0)；制造商以单位产品批发价格w将产品批发给零售商进行销售，设利用废旧品再造出来的产品是与新产品一样同质的，消费者是无法辨识的，且以相同的价格在市场销售，其产品的市场销售价格为p；设市场需求与销售价格相关，市场需求为x(p)=D-kp，其中D是市场规模，k是价格敏感系数；设零售商从消费者手中以价格pr对废旧品进行回收，废旧品的回收量为H(pr)=a+bpr，其中a≥0，b>0，a是回收价格为0时消费者自愿的废旧品回收量，也叫废旧品回收市场初始规模，与消费者的环保意识有关，废旧品的回收价格敏感系数是b；零售商回收的废旧品制造商以价格h进行回收，则0

πr=pQ-prQ0-T(w,δ,φ,h,pr)=p(D-kp)-pr(a+bpr)-T(w,δ,φ,h,pr)

=[(1-δ)p-w](D-kp)+[h-pr+φ(cm-cr)](a+bpr)

(1)

πm=T(w,δ,φ,h,pr)-cm(Q-Q0)-crQ0=T(w,δ,φ,h,pr)-cm[(D-kp)-(a+bpr)]-cr(a+bpr)

=(δp+w-cm)(D-kp)+[(1-φ)(cm-cr)-h](a+bpr)

(2)

πc=(p-cm)Q+(cm-cr-pr)Q0=(p-cm)(D-kp)+(cm-cr-pr)(a+bpr)

(3)

如果选取w、h且对于任意的β>0，满足下列关系式

(4)

2闭环供应链在突发事件下的影响分析

闭环供应链系统在已经协调的情况下，按照协调后的最优生产量Q*进行生产，这时发生了突发事件。销售市场规模和废旧品回收市场初始规模在突发事件下同时变化，设其变化量分别为ΔD和Δa。突发事件发生后，当制造商新的生产量大于原计划生产量时，由于要新增加产品量(Q-Q*)，使得新增加的每单位产品制造商将产生新的成本为λ1；当突发事件导致制造商新的生产量小于原计划生产量时，由于产生剩余产品数量(Q*-Q)，使制造商每单位剩余产品将产生新的处理费用为λ2。此时，零售商的利润πrG、制造商的利润πsG和闭环供应链的利润πcG分别为

πrG=(p-w)(D+ΔD-kp)+(h-pr)(a+Δa+bpr)

(5)

πmG=(w-cm)(D+ΔD-kp)+(cm-cr-h)(a+Δa+bpr)-λ1(Q-Q*)+-λ2(Q*-Q)+

(6)

πcG=(p-cm)(D+ΔD-kp)+(cm-cr-pr)(a+Δa+bpr)-λ1(Q-Q*)+-λ2(Q*-Q)+

(7)

定理1当零售商面临的销售市场规模在突发事件下发生变化时，闭环供应链的最优生产量为

πcG=(p-cm)(D+ΔD-kp)+(cm-cr-pr)(a+Δa+bpr)-λ1(Q-Q*)

πcG=(p-cm)(D+ΔD-kp)+(cm-cr-pr)(a+Δa+bpr)-λ2(Q*-Q)

定理2当废旧品回收市场初始规模在突发事件下变化时，闭环供应链的最优回收价格为

证明当废旧品回收市场初始规模在突发事件下发生变化时，此时闭环供应链的利润为

πcG=(p-cm)(D+ΔD-kp)+(cm-cr-pr)(a+Δa+bpr)-λ1(Q-Q*)+-λ2(Q*-Q)+

由定理2及Q0=a+Δa+bpr可得突发事件后闭环供应链的最优回收量为

定理3突发事件发生导致销售市场规模及废旧品回收市场初始规模变化，如果还采用没有发生突发事件时的收益共享契约T(w,h,δ,φ)，则将打破闭环供应链的协调性。

证明突发事件后仍采用原收益共享契约T(w,h,δ,φ)，由式(4)和式(5)可知零售商的利润为

πrG=(p-w)(D+ΔD-kp)+(h-pr)(a+Δa+bpr)-δp(D+ΔD-kp)+φ(cm-cr)(a+Δa+bpr)

=βπcG+β[λ1(Q-Q*)++λ2(Q*-Q)+]

3闭环供应链在突发事件下的协调应对

根据定理3可得销售市场规模和废旧品回收市场初始规模在突发事件下同时变化时，原有的契约不能实现闭环供应链协调，因此需要对原契约进行调整以实现闭环供应链协调应对突发事件。

定理4原来的收益共享契约调整后为

T(wanti,h,δ,φ)=(wanti+δp)(D+ΔD-kp)-[φ(cm-cr)+h](a+Δa+bpr)

其中wanti=w+β{λ1min[1,(Q-Q*)+]+λ2min[1,(Q*-Q)+]}，并且满足式(4)，则T(wanti,h,δ,φ)能够实现闭环供应链对突发事件的协调应对。

证明当突发事件造成销售市场规模和废旧品回收市场初始规模同时变化，且销售市场规模增大时，由引理1可得闭环供应链的利润为

πcG=(p-cm)(D+ΔD-kp)+(cm-cr-pr)(a+Δa+bpr)-λ1(Q-Q*)

=(p-cm-λ1)(D+ΔD-kp)+(cm-cr-pr)(a+Δa+bpr)+λ1Q*

而采用新的收益共享契约后零售商的利润为

πrG=[(1-δ)p-w-βλ1](D+ΔD-kp)+[h-pr+φ(cm-cr)](a+Δa+bpr)=βπcG-βλ1Q*

当突发事件造成销售市场规模和废旧品回收市场初始规模同时变化，且销售市场规模减小时，由引理1可得闭环供应链的利润为

πcG=(p-cm)(D+ΔD-kp)+(cm-cr-pr)(a+Δa+bpr)-λ2(Q*-Q)

=(p-cm+λ2)(D+ΔD-kp)+(cm-cr-pr)(a+Δa+bpr)-λ2Q*

而采用新的收益共享契约后零售商的利润为

πrG=[(1-δ)p-w+βλ2](D+ΔD-kp)+[h-pr+φ(cm-cr)](a+Δa+bpr)=βπcG+βλ2Q*

由上面的分析可知，采用新的收益共享契约时可实现闭环供应链协调应对突发事件。

4数值分析

设制造商负责制造某种产品让零售商负责销售，用新材料的制造成本为cm=10，利用回收的废旧品再制造成本为cr=5，销售市场规模为D=1000，销售价格敏感系数k=8，废旧品回收市场初始规模a=50，回收价格敏感系数b=20，突发事件发生后制造商生产计划偏离造成的成本损失λ1=3，λ2=2，在突发事件下，ΔD∈[-200,200]，Δa∈[-20,20]。当销售市场规模和废旧品回收市场初始规模在突发事件下同时变化时，采用原有契约和调整后的契约在各种变化水平下所得到的结果如表1所示。

从表1 可以发现：闭环供应链的市场销售价格、生产量只与销售市场规模变化量ΔD成正相关，与废旧品回收市场初始规模变化量Δa无关；回收价格、回收量只与废旧品回收市场初始规模变化量Δa有关，与销售市场规模变化量ΔD无关，且回收价格与Δa成反相关关系，回收量与Δa成正相关关系；闭环供应链的利润与ΔD成正相关，也与Δa成正相关，且ΔD、Δa对闭环供应链的利润产生共同影响；通过在原收益共享契约与调整后的收益共享契约下的闭环供应链利润对比分析，可得闭环供应链利润在调整后的收益共享契约下可实现最优。

表1　不同变化水平下新旧策略对闭环供应链的影响

5结论

本文以单个制造商和单个零售商组成的闭环供应链为研究对象，研究闭环供应链协调应对突发事件问题。研究表明：在正常情况下闭环供应链通过收益共享契约能够实现协调，但当突发事件导致销售市场规模和废旧品回收市场初始规模同时发生变化时，闭环供应链在原有收益共享契约下的协调将失效，但闭环供应链通过调整收益共享契约能够协调应对突发事件。当然，本文研究的只是针对销售市场和回收市场变化的情况，而且考虑的也只是一个周期，实践中突发事件影响的多周期和因素变化更为复杂的情况是要进一步研究的内容。

DAA：三血管序列切面可见升主动脉分出两个分支呈“Y”字形，当右弓占优势时，呈“O”形或梭形血管环。弓降部冠状切面可显示双弓分别发出LCCA、RCCA和RSA、LSA，双弓及左导管均与降主动脉相连[8]。

参考文献：

[1]Clausen J, Hansen J, Larsen J, Larsen A. Disruption management[J]. OR/MS Today, 2001, 28(5): 40-43.

[2]Yu G, Yang J. Optimization application in the airline industry[C]. In Ding Zhu Du and Panos M. Pardalos, Handbook of Combinatorial Optimization, Kluwer Norwell, MA, 1998, 14(2): 635-726.

[3]Yu G, Arguello M, Song M, et al. A new era for crew reeovery at continental airline[J]. Interfaces, 2003, 33(1): 5-22.

[4]Qi X, Bard J F, Yu G. Supply chain coordination with demand disruptions[J]. Omega, 2004, 32(4): 301-312.

[5]Xu M, Qi X, Yu G, Zhang H, Gao C. The demand disruption management problem for a supply chain system with nonlinear demand function[J].Journal systems science and systems engineering, 2003, 12(1): 82-97.

[6]Huang C C, Qi X T, Yu G. Disruption management for supply chain coordination with exponential demand function[J]. Acta Mathematica Scientia, 2006, 26(4): 655-669.

[7]胡劲松,王虹.三级供应链应对突发事件的价格折扣契约研究[J].中国管理科学,2007,15(3):103-107.

[8]Xiao T J, Qi X T, Yu G. Coordination of supply chain after demand disruptions when retailers compete[J]. International Journal of Production Economics, 2007, 109(1-2): 162-179.

[9]王传涛,申金升,纪寿文.生产成本和需求同时变化下供应链的协调[J].计算机集成制造系统,2010,16(6):1307-1312.

[10]盛方正,季建华,周娜.信息不对称时发生突发事件供应链的协调[J].工业工程与管理,2008,13(4):6-10.

[11]曹俊,熊中楷.闭环供应链的研究进展综述及评价[J].物流技术,2010,30(7):126-129.

[12]杨小平,贾明甫.再制造闭环供应链的研究综述及展望[J].物流工程与管理, 2012,34(10): 11-14.

[13]牟宗玉,曹德弼,刘晓冰,李新然.突发事件下两部收费契约协调闭环供应链研究[J].运筹与管理,2013,22(5):35-42.

[14]吴忠和,陈宏,赵千.非对称信息下闭环供应链回购契约应对突发事件策略研究[J].中国管理科学,2013,21(6):97-105.

[15]李新然,胡鹏旭,牟宗玉.第三方回收闭环供应链协调应对突发事件研究[J].科研管理,2013,34(1):99-107.

[16]王玉燕.需求与成本双扰动时闭环供应链的生产策略和协调策略[J].系统工程理论与实践,2013,33(5):1149-1157.