应用通用程序计算深覆盖土层地震反应的几个问题

第一作者 楼梦麟 男，博士，教授，博士生导师，1947年生

应用通用程序计算深覆盖土层地震反应的几个问题

楼梦麟，邵新刚

(同济大学 土木工程防灾国家重点实验室，上海200092)

摘要：讨论了利用ANSYS和LS-DYNA程序进行深覆盖土层地震反应时域计算时所涉及的几个问题。综合前期研究成果，通过对比通用程序的数值计算结果，分析了数值计算时土层计算范围的选取及单元网格划分、阻尼矩阵的形成等对计算精度的影响。分析结果表明：在确定深覆盖土层阻尼矩阵的比例系数时，土层基频与地震激励主要特征频率之间的关系是一个重要影响因素，当前者小于后者，特别是远小于后者时，应基于土层的基频与地震激励的主要特征频率来形成阻尼矩阵的比例系数；竖向、横向网格尺寸及人工边界的选取会对计算的结果造成显著影响。

关键词：深覆盖土层；地震反应；土层范围；有限元网格；Rayleigh阻尼矩阵

基金项目：国家科技支撑项目(2011BAG07B01);国家自然科学

收稿日期：2013-09-30修改稿收到日期：2014-06-19

中图分类号:TU449文献标志码： A

Several problems in seismic response calculation of soil layer with deep deposit using general software

LOUMeng-lin,SHAOXin-gang(State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

Abstract:Several problems in seismic response analysis of soil layer with deep deposit were discussed using ANSYS and LS-DYNA. The effects of some factors, such as, selection of calculation scope of soil layer, division of mesh elements, formation of damping matrix, etc. calculation accuracy were analyzed by comparing the numerical results obtained with the general programs. Numerical examples demonstrated that the relationship between the fundamental frequency of soil layer and the predominant frequency of earthquake excitation is an important factor to affect calculation accuracy; when the former is smaller than the latter, especially, much smaller than the latter, the proportional coefficients in damping matrix should be formed with the two frequencies; the vertical and horizontal grid sizes and the selection of artificial boundary have a significant influence on calculation results.

Key words: soil layer with deep deposit; seismic response; scope of soil layer; finite element mesh; Rayleigh damping matrix

复杂场地的土层地震反应分析对合理确定上部结构的地震动输入参数有重要意义[1]，是进行重要工程场地地震安全性评价工作的主要环节之一[2]。在进行土层地震反应的确定性分析时，通常有两种分析方法，即时域分析方法和频域分析方法。在进行时域分析时，一般采用粘滞阻尼假定，即阻尼力与质点的运动速度成正比，通过求解实系数微分方程组，可求得各土层各自由度地震反应的时程。而在频域分析时，通常采用Fourier变换，通过求解复代数方程组，可求得土层地震反应的稳态解，此时一般采用滞后阻尼假定。这两种分析方法各有不同的适用范围，采用频域法时，可以方便地对线性体系的土层地震反应进行计算，但对于非线性土层地震反应的分析只能采用等效线性化方法[3]，无法进行真非线性分析。而时域分析方法能够适应非线性体系地震反应分析的不同要求，既可以采用等效线性化的分析方法，也可以采用真非线性分析方法[4]。除了简单体系如梁、柱等外，一般工程动力体系地震反应的时域计算多采用直接积分法，一般又分为隐式算法和显式算法。不同特点的程序采用不同方法，如在当前应用广泛的ANSYS程序中采用了隐式直接积分的算法，而在LS-DYNA程序中采用的是显式直接积分的算法[5]。深覆盖土层(泛指土层厚度50 m以上或基本周期1 s以上的土层)地震反应分析时地震工程中经常遇到的问题，针对应用ANSYS和LS-DNYA两个通用程序进行深覆盖土层地震反应分析时所涉及的几个问题进行讨论。

1有限土层计算范围

在实际工程应用中，常把无限域中的地震波传播问题转化为离散体系的振动问题，因此需要合理地把半无限域转化为有限土层的计算体系，本节重点讨论土层地震反应计算中首先遇到的土层计算范围有限化的问题，一般需解决以下几个问题。

1.1地震输入面的确定

在土层的地震反应分析中，有时并不在基岩面输入地震波，采用在土层的假想基岩面处输入地震波的方式计算土层的动力反应。工程中常按以下原则确定假想基岩面[6]：假想基岩面下卧各层岩土的剪切波速均不小于500 m/s；当地面5 m以下存在剪切波速大于其上部各土层剪切波速2.5 m/s的土层，且该层及下卧各层岩土的剪切波速均不小于400 m/s时，可按地面至该土层顶面的距离确定。文献[7]中以上海地区的4个不同深度钻孔为例计算了不同假想基岩面时土层的自振周期和地震反应。数值结果表明：以土层剪切波速500 m/s作为假想基岩面的判别依据并不科学，有时会产生50%左右的计算误差且无规律可言。这是因为土层深度的改变会使土层的自振频率随之变化，使得土层自振频率与输入地震波的频谱特性之间的关系发生变化而致使地震反应产生不同变化；同时从本文“4”的分析中可知，土层自振频率不同也对土层阻尼矩阵的形成产生影响，也会影响地震反应计算的准确性。在当前计算机性能大幅提升的条件下，取深覆盖土层下卧基岩面作为土层地震反应计算的激励面是很有必要的，下卧基岩的弹性变形对深覆盖土层地震反应的影响可以忽略[8]。

1.2侧向竖向人工边界的选择

在土层地震反应计算和土-结构动力相互作用问题的计算中，土层两侧的边界(或称竖向边界)问题曾是广泛关注的课题。基于计算机能力有限的前提下，人们研究了多种人工边界，以期大幅减少计算规模，实现深覆盖土层的动力计算。目前较常用的人工边界有：粘性边界、叠加边界、旁轴边界、一致边界，粘弹性边界、透射边界等。由于粘性边界物理意义清晰，处理方法简单，虽然只有一阶精度，但易于实现。因而一些通用程序得到应用，如在LS-DYNA程序中，有一无反射边界(non-reflecting boundary)即为粘性阻尼边界，其基本思想就是利用边界阻尼力模拟无限域的影响，边界力定义为：

σ法向=-ρcdv法向

(1)

σ切向=-ρcsv切向

(2)

式中:ρ为材料密度，cd和cs分别为压缩波速和剪切波速，v法向和v切向分别为边界法向及切向质点运动速度，σ法向和σ切向分别为无反射边界作用的法向应力及切向应力。

已有研究表明[9-10]，在土层地震反应这类外源激励问题中，粘性阻尼边界并不具备缩减土层范围的有效性，设置远置侧移边界是十分必要的，建议至少应远置5倍土层深度以外。本文以水平均匀土层与河谷地形土层为研究对象，进一步通过应用LS-DYNA计算所得的算例结果来验证上述文献的研究结论。

图1所示水平均匀土层几何尺寸与物理特性如下：土层厚度h为10 m，土介质的弹性模量391 MPa，泊松比0.35，质量密度2 000 kg/m3，阻尼比0.05，剪切波速269 m/s。以地表中点A的加速度及位移反应为研究对象，分别采用粘性边界、侧移边界和固定边界三种形式，边界都在图1的模型两侧施加。共计算了7种工况，分别取L/h=0.5、1、2.5、5、10、20和40。固定边界是指将两端人工边界的节点三个方向自由度全部约束住，侧移边界是指不约束与水平地震激励方向一致的水平自由度，约束其他方向自由度。粘性阻尼边界即在自由人工边界的基础上再附加了产生阻尼力的粘性阻尼器。为了排除竖向网格对于计算精度的影响，本文考虑竖向网格d=λmin/32来进行分析，λmin是指根据地震波有效截止频率fmax所对应的正弦波波长，本文输入ElCentro波(见图2，峰值调整为1m/s2)激励，fmax取为10Hz，竖向网格均取d=1 m。

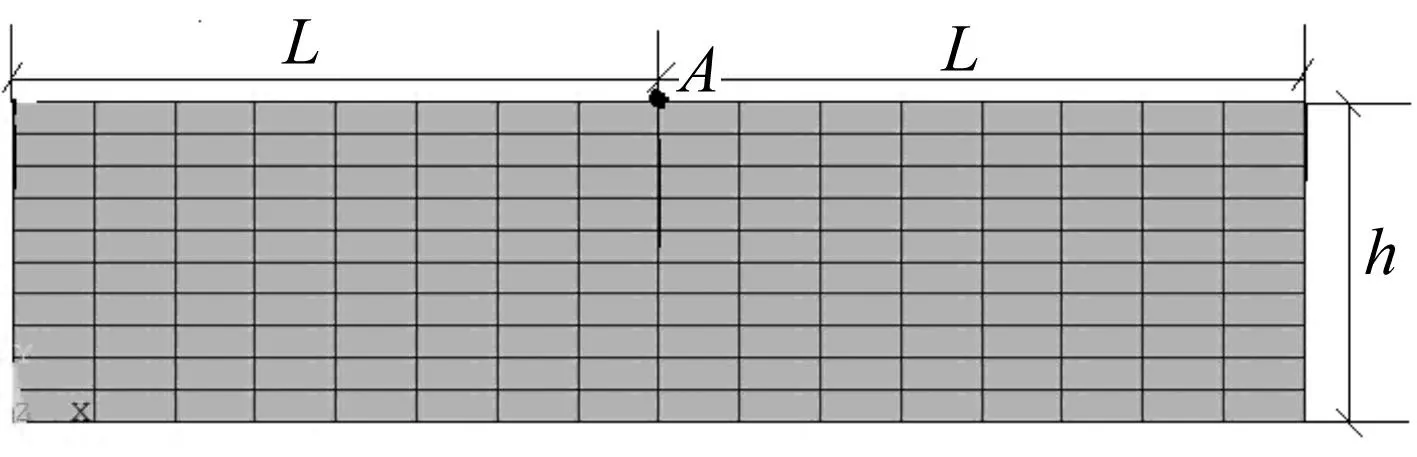
图1　土层有限元网格图 Fig.1 Finite element mesh of soil layer

图2　 El Centro波 Fig.2 El Centro wave

河谷地形土层的材料参数与均匀土层相同，以河谷底部中部位置A点的加速度及位移反应为研究对象，两侧竖向人工边界也采用粘性边界、侧移边界与固定边界，河谷左岸、底部和右岸的土层厚度分别为69 m、65 m和71 m，几何尺寸见图3。该土层设计了6种计算工况，即L1/h1=L2/h2= 2.5、5、10、20、40、60，h1=69 m，h2=71 m。竖向网格划分规则同水平均匀土层。

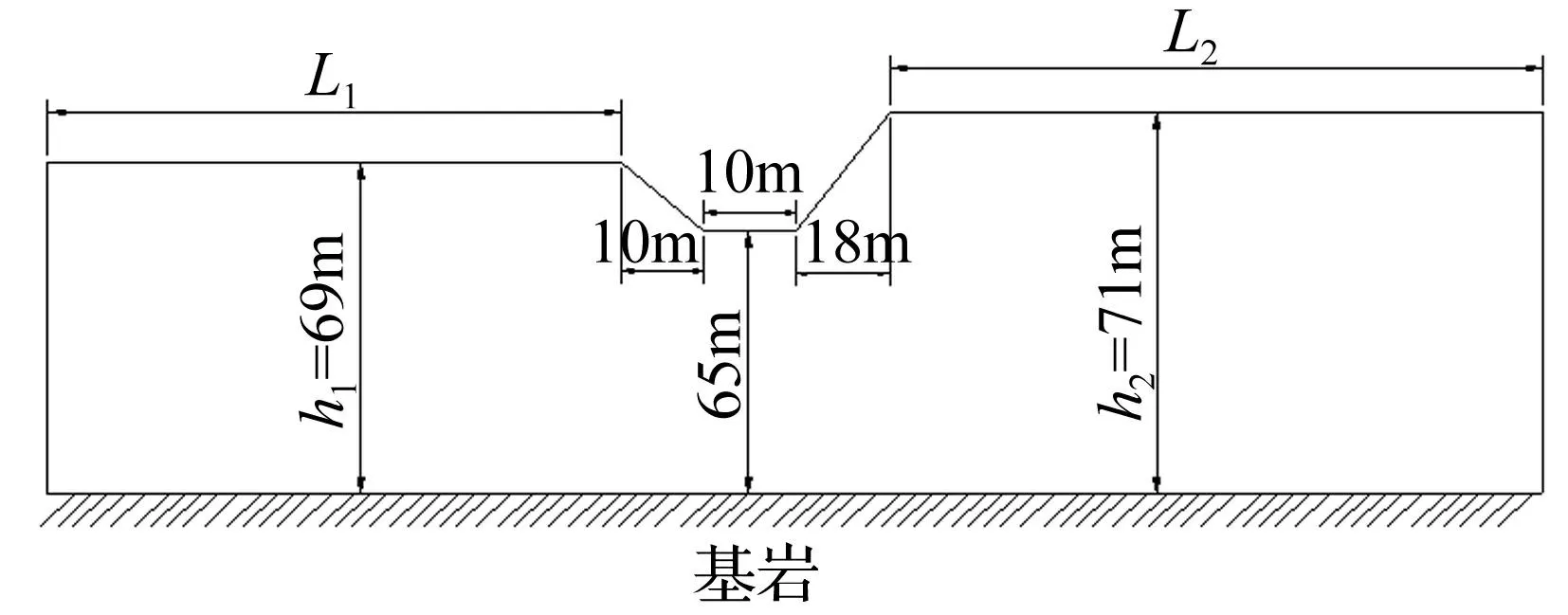
图3　河谷土层 Fig.3 River valley soil layer

1.3土层计算模型的自振频率

三种不同人工边界下，计算所得到的土层基频表1。由表1可知：不同人工边界对水平均匀土层和河谷土层基频的计算值影响显著。固定边界下土层基频最大，自由边界最小。对于水平均匀土层来说，在侧移边界条件下，计算模型所得基频与解析解是相同的[11]。从中可以看出：土层的两侧设为固定边界时，对土层基频计算结果影响最大，自由边界次之，侧移边界对于基频的影响最小。对于固定边界而言，当L/h≥5时，边界对于基频的影响在5%以内，随着L/h的增加，土层基频趋近于侧移边界的。总体上看，对于两种土层，应取L/h(L1/h1和L2/h2)≥5，与以前的分析结论相同。

表1　不同人工边界时土层的基频(单位:Hz)

1.4地震反应计算结果

7种不同计算范围下水平均匀土层顶点A处的加速度峰值和位移峰值见表2。对于水平均匀土层，可通过求解波动方程得到其解析解[11]，其中加速度峰值a=2.15 m/s2，位移峰值u=1.16 mm。不同土层范围有限元计算结果的相对误差表示为：

(3)

式中:amax为水平均匀土层地表中点A处加速度(或位移)峰值有限元解，a*为波动解得到的地表地震加速度(或位移)峰值。加速度和位移峰值的相对误差见表3，从中可看出7种计算工况下有限元解的近似性的变化情况。

表2　 均匀土层A点加速度峰值和位移峰值

表3　均匀土层A点加速度峰值和位移峰值的相对误差(%)

由表2和表3数据可知，当采用固定边界时，均匀土层地震反应的计算结果并不随土层范围的扩大而单调变化，这里涉及到不同的有限元土层范围的土层自振频率与输入地震波频率关系的变化因素，至少要取L为20倍土层深度h时，才能达到计算误差控制在6%以内；而采用粘性边界时，数值计算结果变化情况与固定边界相类似，总体上加速度的计算结果要优于固定边界，这是由于边界阻尼器的设置，能够消除部分人工边界上的反射能量，但是效果仍不如侧移边界。对于固定边界及粘滞边界而言，在L/h很小时边界范围取值对土体基频的影响非常显著，这是造成在这两种边界条件下土层地震反应计算结果误差很大的主要原因。特别是在自由边界条件下，当土层范围取得较小(如L/h≤1)时，土层基频远远低于解析解，即使土层范围取得较广，但土层基频仍与解析解有一定差距。我们知道，低频分量对土层位移反应的贡献要远远大于对土层加速度反应的贡献[12]，因此自由边界造成土层基频变小致使在位移反应中，粘滞边界下的位移计算精度在很多情况下不及固定边界，特别是在L/h=0.5时，土层基频减低1.5倍，致使位移峰值增大3倍多。而侧移边界下土层基频并不随L/h的变化而变化，这样也保证了计算的精度。显然对于水平均匀土层，无论土层范围取多大，侧移边界下的计算精度都很好，这是因为水平地震作用下分层均匀土层地震反应分析为反对称问题，两侧的侧移边界正好适应了这一问题的对称性条件，因此可用两侧具有侧移边界的单排单元的土条来计算水平地震作用下分层均匀土层的地震反应[13]。

对于河谷地形土层，由于没有解析解，以6种工况中L/h1=L/h2=60时的土层地震反应为比较基准，相关计算结果见表4、表5，可近似看出其他5种计算工况下河谷土层地震反应解的近似性。

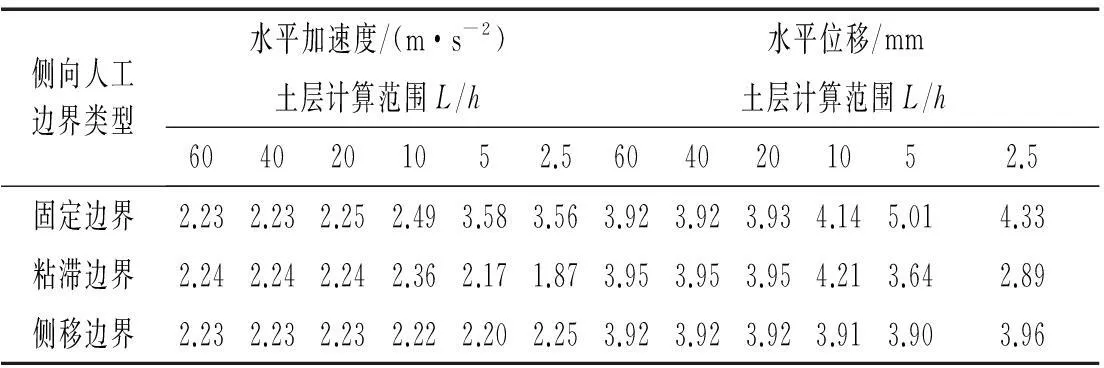
表4　河谷土层中A点的加速度峰值和位移峰值

表5不同计算范围时A点加速度峰值

和位移峰值的相对误差(%)

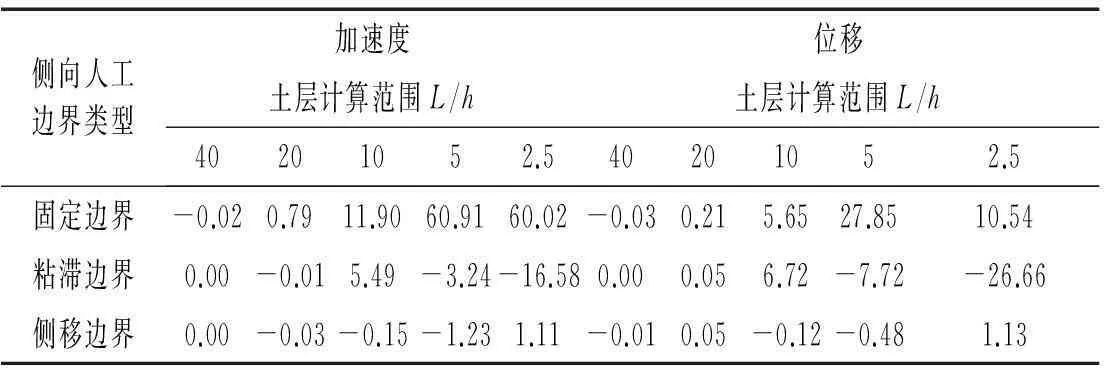
Tab.5 Relative error of peak acceleration and displacement at point A of River valley soil layer(%)

由表4和表5可以看出，河谷地形的地表A点的加速度或者位移在20倍边界以上时基本没有区别，误差很小。对于固定边界，当L/h1=L/h2≤10时，计算结果误差很大，粘性边界相对于固定边界，计算精度总体上要好很多，但是在L/h1=L/h2=2.5时，粘性边界下土层位移反应的误差要大于固定边界，其原因也是自由边界下，土层基频下降较多。对于侧移边界，当2.5≤L/h1=L/h2≤40倍时，计算误差都在2%以内，精度较高。

结合以前和现在的分析结果，采用ANSYS、LS-DYNA进行深覆盖土层地震反应计算时，宜采用远置侧移人工边界，一般单侧范围宜取土层厚度的5倍以上。土层在竖向地震激励下的地震反应计算精度对有限范围大小取值的敏感性不及水平激励时突出，实际工程计算中，如要进行竖向地震输入，必有水平地震输入，因此按水平基底运动输入所确定的土层有限范围完全适用于竖向基底运动输入时土层地震反应的计算。

2计算网格划分的要求

对于动力分析问题，当连续介质离散为有限单元时，就有了滤波和散射作用[14]，动力分析中应重视单元划分中的尺度问题，使得在有效激励频率范围内，计算的精度得到保障。

2.1竖向网格尺寸

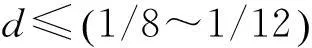
2.2横向网格尺寸

3阻尼矩阵建模方式对地震反应计算的影响

3.1地震反应分析方程中的阻尼矩阵

在进行复杂土层的地震动力反应时域分析时，一般采用集中质量的有限元方法。对计算体系进行离散化处理后，可以得到如下动力方程式：

(1)

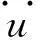
[C]=a0[M]+a1[K]

(2)

式中：a0和a1为比例常数。利用振型正交性，可得：

(3)

式中:ωm、ωn和ξm、ξn分别为计算体系第m、n阶振型的自振频率及对应的阻尼比。振型阻尼比是动力体系耗能特性的宏观描述，对土层介质来说易于从室内土样实验和实测试验中获取。当各阶振型阻尼比相同时，即ξm=ξn=ξ，上式可简化为:

(4)

这样由式(4)确定的第i阶振型阻尼比的计算值为：

(5)

式(5)表示的第i阶振型阻尼比与第i阶自振频率之间的关系(见图4)。

图4　振型阻尼比与频率的关系 Fig.4 Relationship of modal damping ratio and frequency

在土动力分析中，土层体系的阻尼矩阵也常采用如下只与质量矩阵成比例或与刚度矩阵成比例的形式。

(6)

(7)

这两种单参数阻尼矩阵所产生的各阶振型阻尼比随频率变化的趋势也列入图4中。很显然，在质量比例的阻尼矩阵下，动力体系的各阶振型阻尼比随频率升高而降低，而在刚度比例阻尼矩阵下，动力体系的各阶振型阻尼比随频率升高而线性增大。

由于深覆盖土层的自振周期较长，因此其低阶自振频率远小于基岩地震波中的主要分量的激振频率。已有研究表明：对于这类长周期动力体系(指低阶振型频率远小于外部动力荷载或动力作用中主要分量的激励频率的动力体系)在建立动力体系阻尼矩阵时，必须重视外部动力激励中主要频率成分的影响，对于深覆盖土层地震反应同样需加以关注。下面根据我们的研究成果，结合ANSYS和LS-DYNA两个计算软件的阻尼建模功能，介绍进行深覆盖土层地震反应分析时合理地建立阻尼矩阵应关注的问题。

3.2ANSYS软件

应用ANSYS程序进行深覆盖土层地震反应计算时，可采用多种形式的阻尼矩阵，其中最常用的是式(2)所示Rayleigh阻尼和式(7)所示的刚度比例阻尼矩阵。前者为双参数模式，后者为单参数模式。在两种计算模式并存的情况，双参数模式的可调控性较好，建议在进行深覆盖土层地震反应分析时不要选用式(7)，下面讨论如何选双参数。对于一般工程结构而言，因为低阶振型在结构的地震反应中起主导作用，一般选取体系基频及其所对应的振型阻尼比来确定比例系数，即取ωm=ω1=2πf1；设ωn=2πf，如何选取f是建立Rayleigh阻尼矩阵应加以特别关注的问题。通常选取动力体系的第2阶自振频率f2或第3阶自振频率f3及其对应的振型阻尼比。我们研究[18]表明对深覆盖土层而言，这一选取方法是不可取的，应选取基岩输入地震波反应谱的峰值频率fR。这样可以保障在土层第1阶振型和主要激励频率相近的高阶振型对土层地震反应的贡献的正确性，从而使深覆盖土层地震反应计算更加准确。

3.3LS-DYNA软件

应用LS-DYNA程序进行深覆盖土层反应计算时采用显式算法的质量比例阻尼矩阵进行直接积分，为此取：[C]=a0[M]，并建议:

a0=2ω1ξ

(8)

式中：ω1为土层的基频，ξ为土层的振型阻尼比，一般假定土层各阶振型阻尼比相同。以ω1来确定比例系数a0符合人们的常规的认识，即在结构体系地震反应中，第1阶振型频率贡献最大。当土层基频接近于或高于输入地震的主要频率分量时，显然由于土层第1阶振型的振型参与系数大，其对体系地震反应的贡献远大于其他高阶振型，因此当第1阶振型阻尼比与实际阻尼比相等时，在第1阶振型地震反应计算正确得到保证的前提下，其他高阶振型阻尼比偏小时使得土层地震反应的计算误差非常有限。而当计算体系的基频远低于输入地震波的主要频率分量时，很显然与地震波中主要频率分量相近的土层高阶振型将存在共振效应。众所周知，共振放大因子为Di=1/(2ξi)，显然当低估振型阻尼比时，将高估共振放大因子，从而使得该振型的地震反应计算值增大。例如当ω1/ωi=1/2时，则Di增大1倍，依此类推，此时高阶振型的共振效应不可忽略。根据我们的研究成果[19]，在质量比例的阻尼模型中，应对式(8)进行修正，采用如下计算公式：

a0=2ωeξ

(9)

式中：ωe为待定的频率参数。当土层基频ω1小于输入基岩地震波反应谱峰值频率ωR(ωR=2πfR)时，建议采用取为土层基频ω1和输入地震波反应谱峰值频率ωR的算术平均值，基本可保证计算所得土层加速度峰值略高于真实解。

4结论

在深覆盖土层地震反应时域计算中，应特别关注土层有效范围的选取、计算网格划分、阻尼矩阵形成方式等问题，处理不当会严重影响计算结果的可靠性。

(1) 深覆盖土层地震反应计算中取下卧基岩面作为土层地震反应计算的地震激励面是很有必要的；土层计算时侧移边界的计算效果很好，宜采用远置侧移人工边界，单侧范围一般宜取5倍以上土层厚度。

(3) 在深覆盖土层地震反应的隐式计算中，Rayleigh阻尼矩阵建模时，除取其中一个振型频率ωm为土层基频外，建议另一个频率ωn取为输入基岩地震波反应谱的峰值频率ωR；在显式计算中，形成质量比例阻尼矩阵时，建议ωs取为土层基频和输入地震波反应谱峰值频率的算术平均值，基本可保证计算所得土层加速度峰值略高于真实解。

参 考 文 献

[1] 廖振鹏．近场波动问题的有限元解法[J]．地震工程与工程振动，1984, 4(2)：1-14．

LIAO Zhen-peng. A finite element method for near-field wave motion in heterogeneous materials[J]. Earthquake Engineering andEngineering Vibration, 1984, 4(2): 1-14.

[2] GB 17741-2005. 工程场地地震安全性评价[S]. 北京：地震出版社，2012.

[3] Martin P P, Seed H B. One-dimensional dynamic ground response analyses [J]. Journal of the Geotechnical Engineering Division, 1982, 108(7): 935-952.

[4] 李小军，廖振鹏，关慧敏．粘弹性场地地形对地震动影响分析的显式有限元-有限差分方法[J]．地震学报，1995, 17(3)：362-369．

LI Xiao-jun, LIAO Zhen-peng, GUAN Hui-min. An explicit finite element-finite difference method for analyzing the effect of visco-elastic An explicit finite element-finite difference method for analyzing the effect of visco-elastic Local topograph on the earthquake motion [J]. ACTA Seismologica Sinica, 1995, 17(3): 362-369.

[5] 尚晓江，苏建宇，王化锋．ANSYS/LS-DYNA 动力分析方法与工程实例[M]．北京：中国水利出版社，2008.

[6] GB50011-2010. 建筑抗震设计规范 [S]. 北京：中国建筑工业出版社，2010．

[7] 上海市地震局、同济大学．上海市地震动参数区划[M]．北京：地震出版社，2004.

[8] 潘旦光，楼梦麟．基岩弹性刚度对土层地震反应的影响[J]．地震工程与工程振动，2004(4)：158-163．

PAN Dan-guang, LOU Meng-lin. Influence of rock stiffness on seismic response of layered soil [J]. Earthquake Engineering and Engineering Vibration, 2004(4): 158-163.

[9] 楼梦麟，潘旦光，范立础．土层地震反应分析中侧向人工边界的影响[J]．同济大学学报，2003, 7(7):757-761．

LOU Meng-lin, PAN Dan-guang, FAN Li-chu. Effect of vertical artificial boundary on seismic response of soil layer[J]. Journal of Tongji University , 2003, 7(7): 757-761.

[10] 乔冠东，楼梦麟．大型沉井基础地震反应分析中侧向边界的影响[J]．工程力学，2012, 26(S1): 111-114．

QIAO Guan-dong, LOU Meng-lin. Effect of vertical artifical boundary on seismic responses analysis of large-scale open caisson [J]. Engineering Mechanics, 2012, 26(S1): 111-114.

[11] 潘旦光，楼梦麟，董聪．一致输入作用下土层的地震反应分析[J]．计算力学学报，2005, 22(05): 562-567．

PAN Dan-guang, LOU Meng-lin, DONG Cong. Seismic response analysis of soil layer under uniform excitation[J]. Chinese Journal of Computational Mechanics, 2005, 22( 05):562-567.

[12] 楼梦麟，董云．加速度反应谱规准化对场地位移反应的影响[J]．震灾防御技术，2014，9(2)：149-158.

LOU Meng-lin, DONG Yun. Effect of normalizing acceleration response spectra on displacement time history[J]. Technology for Earthquake Disaster Prevention, 2014, 9(2): 149-158.

[13] 邬都，楼梦麟．水平成层土层地震反应分析的一维有限元方法[J]．震灾防御技术，2008( 01): 45-52．

WU Dou, LOU Meng-lin. Seismic response analysis in horizontal layer with 1-D finite element method [J]. Technology for Earthquake Disaster Prevention, 2008(01): 45-52.

[14] 宗福开．波传播问题中有限元分析的频散特性及离散化准则[J]．爆炸与冲击，1984, 4(4): 16-21．

ZONG Fu-kai. Frequency-dispersion characteristics and discretization of the finite element analysis in wave propagation problems [J]. Explosion and Shock Waves, 1984, 4(4): 16-21.

[15] 白建方，楼梦麟．复杂场地土层有限元建模的两个问题研究[J]．岩土工程界，2008, 11(9): 27-30．

BAI Jian-fang, LOU Meng-lin. The two problems research of finite element modeling of complex ground soil [J]. Geotechnical Engineering World, 2008, 11(9): 27-30.

[16] 杨燕，楼梦麟．汶川地震中远场深覆盖土层动力反应分析[J]．防灾减灾工程学报，2011, 31(4): 462-468．

YANG Yan, LOU Meng-lin. Dynamic response analysis of far-field soil layer with deep deposit during wenchuan earthquake [J]. Journal of Disaster Prevent and Mitigation ENG, 2011, 31(4): 462-468.

[17] 白建方，楼梦麟．行波输入下土层有限元网格的划分原则[J]．世界地震工程，2009, 25(1): 48-51．

BAI Jian-fang, LOU Meng-lin. Partition principle of the finite element meshes of soil under traveling wave excitations [J]. World Information on Earthquake Engineering, 2009, 25(1): 48-51.

[18] 楼梦麟，邵新刚. 深覆盖土层Rayleigh阻尼矩阵建模问题的讨论[J]. 岩土工程学报,2013, 35(7): 1272-1279.

LOU Meng-lin,SHAO xin-gang. Discussion on modeling issues of Rayleigh damping matrix in soil layers with deep deposit [J]. Chinese Journal of Geotechnical Engineering,2013, 35(7): 1272-1279.

[19] 楼梦麟，邵新刚. 土层地震反应显式计算中阻尼矩阵系数的选取[J]. 同济大学学报,2013,41(8):1126-1132.

LOU Meng-lin, SHAO Xin-gang.Coefficient selection of damping matrix in explicit calculation of soil layer seismic response [J]. Journal of Tongji University, 2013,41(8): 1126-1132.