局部约束结构振动的模态研究

第一作者 李金录 女，硕士生，1988年生

通信作者 丁千 男，教授，1963年生

邮箱：qding@tju.edu.cn

局部约束结构振动的模态研究

李金录1，丁千2

(1.天津大学 力学系，天津300072; 2.天津市非线性动力学与混沌控制重点实验室，天津300072)

摘要：制动盘/摩擦块系统的制动过程属于局部接触振动问题。摩擦块局部接触(约束)会对系统模态及固有频率造成影响，进而影响制动噪声的产生。将刹车盘简化为一维循环梁结构，并建立了在摩擦块作用下的运动方程。首先计算无接触时梁自由振动的模态(参考模态)。然后用线性弹簧代替局部接触，列写出连续条件并计算模态，得到所谓局部非连续基函数。将局部非连续基函数与参考模态进行正交化处理后，作为参考模态的补充，用于计算系统响应。与差分法结果比较表明，与传统模态方法相比，局部非连续基函数法更为准确。研究发现局部接触会抑制循环结构振动的对称性，导致正弦或余弦模态消失，以及刚度非线性和摩擦作用，会使振动是波动型的。该工作为基于局部非连续基函数法研究摩擦结构不稳定振动机理打下了基础。

关键词：摩擦盘；振动；模态；局部非连续基函数法

基金项目：国家自然科学基金资助项目(11272228);高等学校博士学科点专项科研基金资助项目(20120032110011)

收稿日期：2013-07-23修改稿收到日期：2014-01-21

中图分类号:TB533文献标志码： A

Modal approach for vibration of a structure with local constraints

LIJin-lu1,DINGQian2(1. Department of Mechanics, Tianjin University, Tianjin 300072, China;2. Tianjin Key Laboratory of Nonlinear Dynamics and Chaos Control, Tianjin 300072, China)

Abstract:Braking process of a brake disc is a vibration problem with local contacting, local contact has an influence on the modes and natural frequencies of the disc system. The method of local discontinuous basis function can be used to estimate the modes of the system accurately. Here, a brake disc contacted by a brake boot or a friction block was simplified as a one-dimensional beam with loop structures. Its equation of motion was established. Firstly, the free vibration modes of the beam without contact defined as the reference modes were calculated. Then the contact of the friction block was simplified as several linear springs. Using the continuous conditions, the system’s modes were calculated and orthogonalized with the reference modes, they were taken as the supplements of the reference modes and named the local discontinuoas basis functions. They were used to calculate the system response. Based on the discontinuous mode analysis, vibration of the brake disk under action of external excitation is calculated. The results showed that the local discontinuous basis function method is more accurate than the traditional modal method; the local contact of the friction piece can restrain the vibration symmetry of the brake disc to lead to disappearance of sine or cosine modes; nonlinear stiffness and friction make the vibration be wave type. This study laid a foundation for studying unstable vibration mechanism of structures with friction using the local discontinuous basis function method.

Key words: brake disc; vibration; model; local discontinuous basis function method

摩擦制动噪声机理研究包括滞-滑自激振动(stick-slip)机理和结构不稳定振动机理。滞-滑振动的典型物理模型为质量块-平置/斜置移动带模型，采用非线性摩擦力模型进行研究，结果十分丰富[1]。随着计算条件提高，人们开始注重从结构不稳定角度解释制动噪声，例如应用有限元和模态综合技术进行建模，揭示结构参数不匹配对不稳定模态的影响[2]。Hochlenert[3]指出，摩擦和结构的非线性耦合提高了耦合固有频率，增加盘的旋转能量向面外振动转移，使尖叫能量更大。新的实验技术也应用于刹车盘的振动和噪声测试，如多普勒和全息摄影技术[4-5]。一些实验也证明，摩擦盘的尖叫现象是摩擦块与盘相互作用而产生的面外振动所造成的[6]。实验和计算还发现，局部接触使得盘失去振动轴对称，存在由双重特征频率模态分裂导致的正、余弦模态尖叫和转动尖叫三种可能(取决于刹车片尺寸与刹车盘的弯曲模态波长比值，并与结构非线性耦合有关[7])。

有些工程结构存在局部约束现象，受力描述可以是光滑非线性(例如摩擦接触)，也可以是分段线性或非线性(例如间隙、冲击)[8]。局部约束会对系统模态产生影响，进而影响系统动力学行为。由于局部约束造成模态内力或剪力产生跳跃(模态曲线仍是连续的)，Segalman[9]提出局部非连续基函数方法，即以线性刚度代替局部约束后求得模态函数，作为不考虑约束时的参考系统模态函数的补充，共同构成原系统的模态(基)函数。对结构铰接点摩擦局部非线性引起的模态非光滑现象进行了研究，并得到实验验证。

制动系统振动模型属于局部接触(摩擦)非线性系统。针对局部非连续基函数方法的应用，对简化的刹车盘系统进行降维，分析局部约束对循环结构模态的影响，作为准确计算摩擦盘噪声振动的基础。

1摩擦盘简化振动模型

摩擦盘是一个三维环形盘。若忽略面内径向运动和扭转，只考虑主要影响摩擦噪声的圆盘边缘处的面外运动，可近似转化成研究一维梁的横向振动。由于梁左右两端力学边界条件是接续的，从而构成一维循环梁结构[9]，如图1(a)所示。将与摩擦盘接触的摩擦块离散成均布的若干质量块(见图1(b))，应用Hamilton原理推导出包含非线性变形因素的梁的横向振动方程：

图1　刹车盘/摩擦块系统及简化 Fig.1 The simplified model of brake disc/friction block system

-L1(x,t)δ(x-xi)

(1)

其中:xi是质量块所在位置的轴向坐标，δ是单位脉冲函数。L1(x,t)中包含质量块所在位置的横向恢复力、局部转动造成的摩擦力投影、弹性变形产生的力矩及质量块惯性力，如下式：

其他各符号的含义见表1。

只研究局部接触对梁横向振动模态的影响，暂不考虑摩擦块在盘面内的复杂运动。

表1　符号及含意

2构造局部非连续基函数

2.1参考系统基函数

若不考虑摩擦块局部接触(约束)，即得到线性参考系统，其自由振动方程为

(2)

取如下形式响应

(3)

式中:n=1, 2, 3…。φn(x)是系统(2)的第n阶弯曲模态，也称参考模态或基函数，ηn(t)是相应的模态振幅。假定梁受到横向支撑运动y激励下产生振动，则其弹性变形为u(x,t)=w(x,t)-y(x,t)。自由振动时u(x,t)=w(x,t)。由于图1所示循环梁的两端具有相同的位移和力边界条件，因此选择同时包含正弦和余弦函数作为模态函数。参考模态和对应的频率是：

(4)

(5)

当模态阶数n为奇数时，第n阶与第n+1(偶数)阶模态频率相同，每个频率值对应一个正弦模态和一个余弦模态，即具有双模态特性。这是由循环系统模型的轴对称性所产生的现象。

2.2局部非连续基函数

将摩擦块/盘接触约束简化成一个刚度系数k的线性弹簧(也称附加线性弹簧)，作用于接触部位中部，得到约束线性化系统。左右两段梁的振动连续条件为(若有多个约束部位简化成附加线性弹簧，则所有相邻梁都需要给出连续条件)

u1,xx(-L,t)=u2,xx(L,t),u1,xxx(-L,t)=u2,xxx(L,t)

u1(0,t)=u1(0,t),u1,x(0,t)=u2,x(0,t)

u1,x(0,t)=u2(0,t),

EI(u1,xxx(0,t)-u2,xxx(0,t))=ku2(0,t)

(6)

式中：

u1(x,t)：x∈(-L,0);u2(x,t)：x∈(0,L)

两段梁的响应分别取如下形式

(7)

式中:ψmj(x)是约束线性化循环梁的弯曲模态，取如下形式

(8)

对应的频率为

(9)

式中：λj为受到附加线性弹簧个数的影响，其形式是一个超越函数，只能计算得到近似值。式(8)表达的两段梁的模态位移是连续的，但一次导数是间断的。表明局部约束点的模态内力或剪力产生跳跃，因此称为局部非连续基函数。

2.3构造局部接触系统的响应

(10)

其中，j=2, 3, …，N为参考模态数量。proj定义为(引入向量v1和v2来说明)

因此，梁的振动响应

(11)

其中ηn和ηmj由模态方程确定

(12)

(13)

式中:j表示非连续基函数的阶数。

3计算分析

3.1确定附加线性弹簧刚度

将接触约束用一个刚度系数k的线性弹簧代替，计算得到约束线性化系统固有频率随着k值的变化(见图2)。为使非连续基函数能够恰当描述约束的影响，k值不应过大或过小，而是选在0-∞的变化过程中，固有频率变化趋势产生转换的地方，即拐点处的值。由图2可知，k约取为106.6N/m。

图2　约束线性化系统固有频率与线性刚度的关系 Fig.2 the relationship of inherent frequency and linear stiffness of reference system

3.2局部约束对循环梁模态的影响

表2给出了参照系统和约束线性化系统的前5阶固有频率。可以看出，参照系统第一阶固有频率=0，分别对应平动和转动两种刚体运动。所有其他非零固有频率都为双频率，即每个频率值均对应一个正弦模态和一个余弦模态，即系统具有双模态特性(这是循环对称系统的特点)，参见图3。

图4为约束线性化系统的模态。附加线性弹簧带来两个明显变化：① 原有第1阶刚体模态转变成产生弹性变形的模态，约束处为其波峰；② 破坏了原结构的振型对称性，导致双模态特征频率分离。见表2中第2阶线性基函数频率对应的是正弦及余弦两种模态，弹簧的引入使得原频率分离成两个频率成分，且对应的皆为余弦模态，这是由于附加弹簧正好作用在正弦振型的零点和余弦振型的波峰处，因此第2阶正弦成分被抑制，而对余弦成分的影响并不大。在第2阶模态后，正弦成分均消失，失去双模态特性。另外，表2还表明各阶模态频率较参照系统有所增加。这些结果与实验基本一致[12]。

图3　参照系统模态 (b)、(c)、(d)、(e)分别代表 第1、第3、第4、第5阶模态 Fig.3 Modes of the reference system

Tab.2 The comparison of basis function of frequency

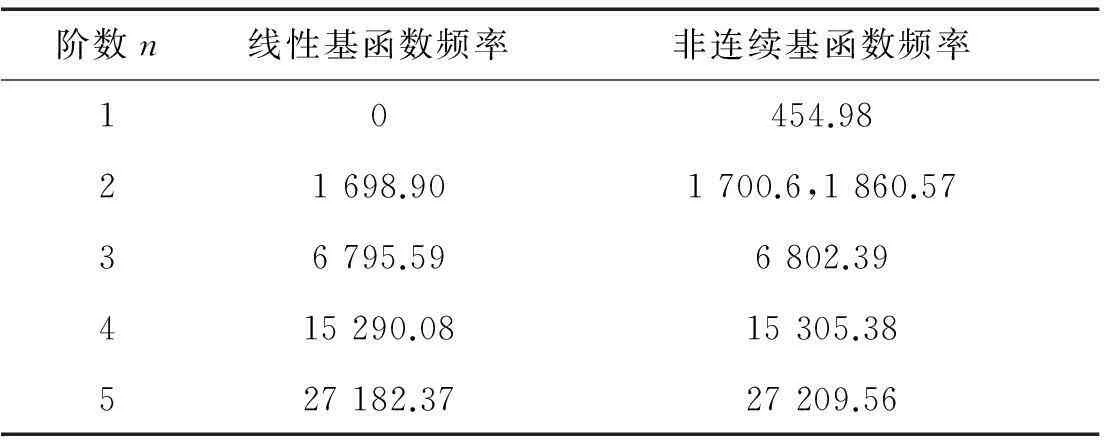
阶数n线性基函数频率非连续基函数频率10454.9821698.901700.6,1860.5736795.596802.39415290.0815305.38527182.3727209.56

图4　约束线性化系统模态 (a)、(b)、(c)、(d)、(e)分别代表 第1、第2、第3、第4、第5阶模态 Fig.4 Modes of the constraint system

3.3非连续基函数的正交化

按照局部非连续基函数方法，若只有一处局部约束，计算系统响应一般只需考虑附加一个线性弹簧得到的约束线性化系统的第1阶非连续基函数。若局部约束的相对范围较大，则可以在约束范围内依次引入多个附加线性弹簧，分别得到第1阶非连续基函数并进行正交化处理，得到相应的模态。最后，通过线性叠加来分析系统响应。对于循环系统，依次引入的多个附加线性弹簧的刚度应该取相同的值。

引入一个线性弹簧，由式(10)得到与前N阶参照系统模态正交化和归一化后的非连续基函数函数

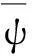
2.019 0×10-4×cos(34.783x)-5.475 3×10-2cos(8.695 7x)-

0.311 28cosh(4.5x)-1.719 3×10-4sin(8.695 7x)-

2.015 4×10-5sin(17.391x)-2.535 9×10-6sin(34.783x)-

7.953 0×10-5cos(43.478x)+0.288 49sin(4.5x)-0.287 96sinh(4.5x)-

1.248 9×10-6sin(43.478x)-6.234 2×10-4cos(26.087x)-5.872 9×10-6sin(26.087x)

( 14)

2.019 0×10-4cos(34.783x)-5.475 3×10-2cos(8.695 7x)-

0.312 21cosh(4.5x)-1.719 3×10-4sin(8.695 7x)-

2.015 4×10-5sin(17.391x)-2.535 9×10-6sin(34.783x)-

7.953 0×10-5cos(43.478x)-0.288 44sin(4.5x)+0.288 98sinh(4.5x)-

1.248 9×10-6sin(43.478x)-6.234 2×10-4cos(26.087x)-5.872 9×10-6sin(26.087x)

(15)

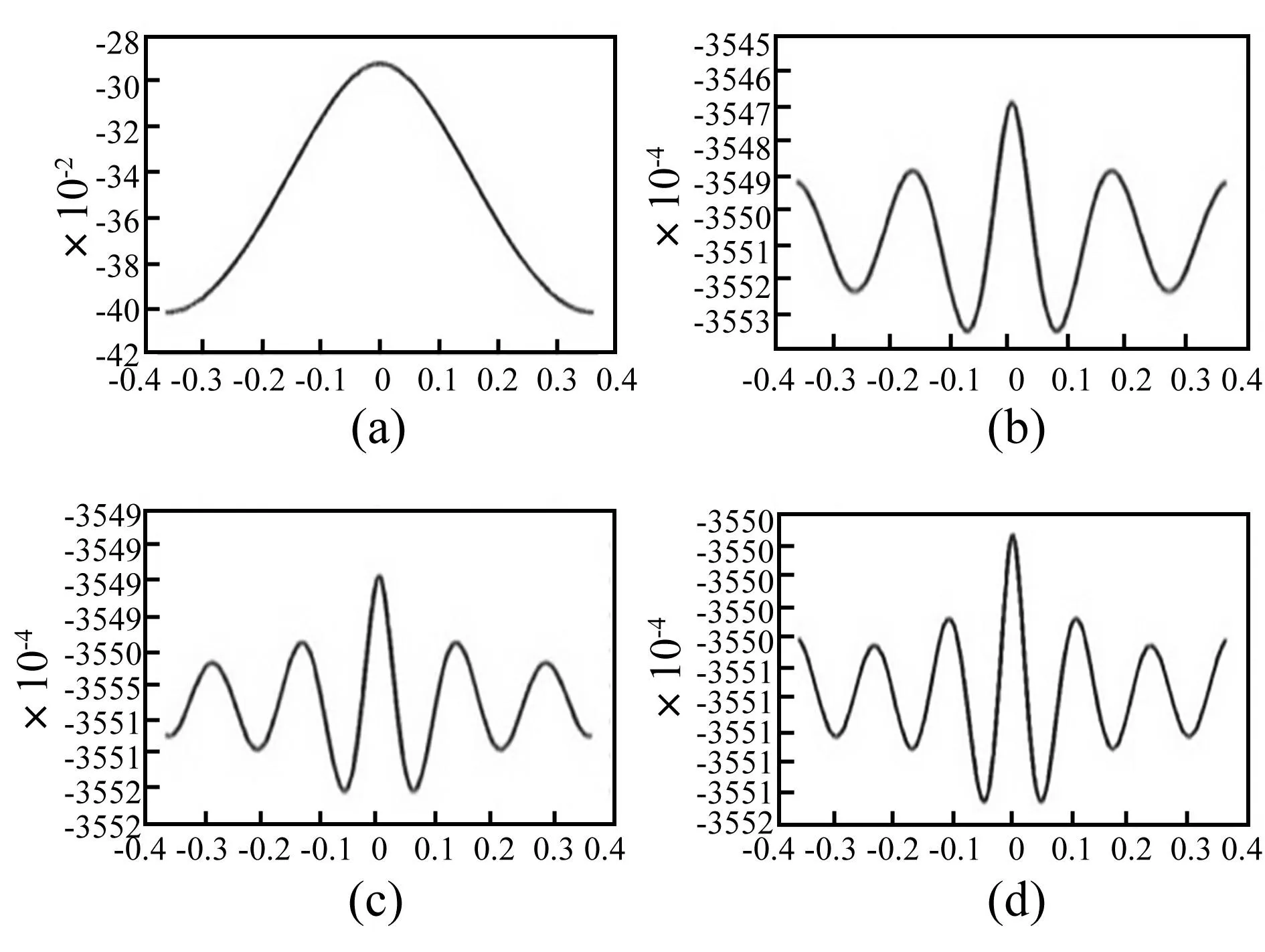
图5　正交化后非连续基函数 Fig.5 The discontinuous basis function after the orthogonalization (a)、(b)、(c)、(d)分别代表与0阶，6阶， 8阶，10阶参考模态正交化的约束模态

3.4振动响应计算

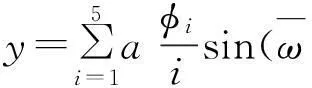
为验证非连续基函数的正确性，将约束线性化为一个附加弹簧，计算得到图6所示循环梁的响应挠曲线。响应振型函数选用两种情况：振型A中全部为非连续基函数(针对约束线性化循环梁，该基函数是准确的模态函数)，振型B是由参考基函数加上第一阶非连续基函数构成。可以看出，共振挠曲线形状基本相似，只是高阶共振挠曲线形状出现少许差异。因此，应用非连续基函数法(即，以非连续基函数作为传统基函数的补充)，可以得到较准确模态函数。

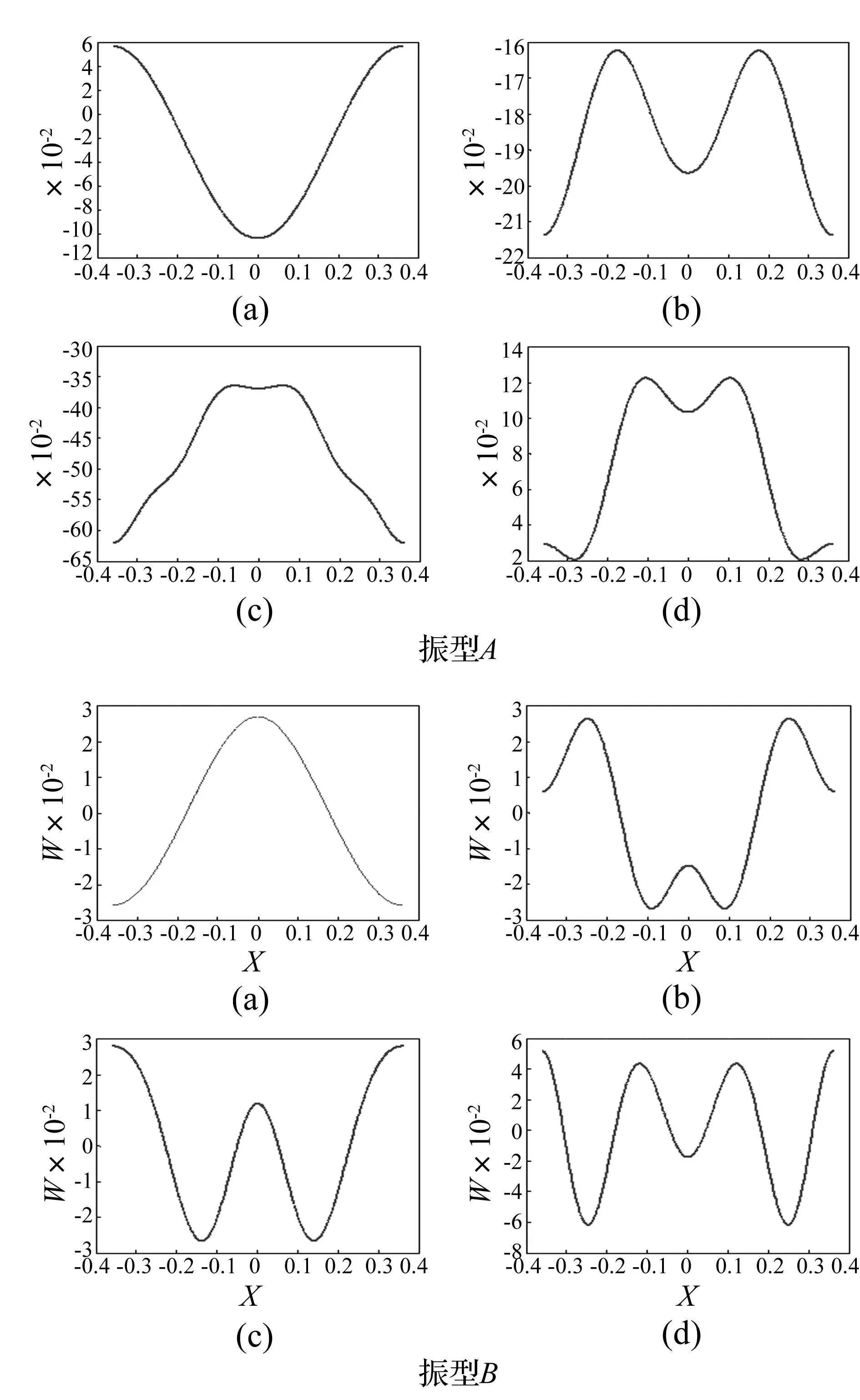
图6　响应挠曲线图 Fig. 6 The chart of flexural response (a)、(b)、(c)、(d)分别代表与激振频率分别为的第2、 第3、第4、第5阶系统固有频率时的响应挠曲线图

考虑到实际摩擦块范围较大(约占摩擦盘边缘周长的1/5～1/4)，我们将摩擦块简化成均匀分布的三个质量块。对应于每个质量块，分别计算接触约束的第一阶非连续基函数。将三个非连续基函数(实际上只有相位的差别)均作为传统基函数的补充，计算循环梁各阶共振时的挠曲线，并与仅按照传统模态方法和差分法的结果进行了比较(见图7)。

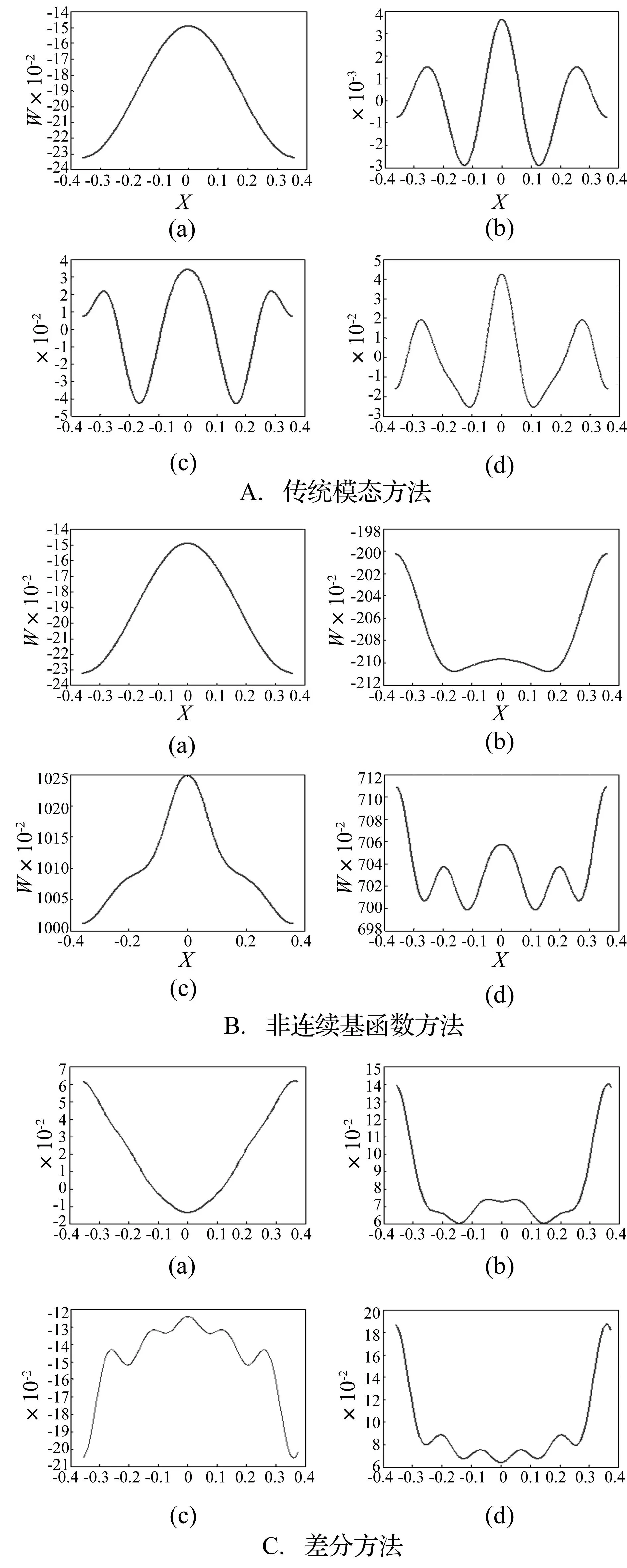
图7　响应挠曲线图 Fig.7 The chart of flexural response (a)、(b)、(c)、(d)分别代表与激振频率分别为的第1、 第3、第4、第5阶系统固有频率时的响应挠曲线图

总体上看，相对于传统基函数方法，非连续基函数方法得到的各阶共振曲线与差分法计算结果更为接近。由图8(c)可见，由于考虑了约束的作用，约束位置的响应明显较小，且摩擦盘的整体响应幅值减小，充分体现出了局部约束对摩擦盘响应的抑制作用。

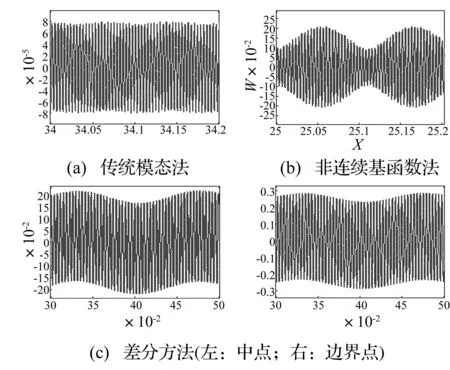
图8　梁中点的时间历程(第二阶共振) Fig.8 The chart of time course with the midpoint of the beam

第2阶共振时，梁中点的响应如图8所示。参照系统中，由于求解响应时忽略了刚体位移(即零频率模态)，计算出的振动幅值很小，不能充分体现振动的真实情况[11]。应用非连续基函数法过程中，由于考虑了弹簧的约束住用，把一个循环体分成两个独立的单元来计算，此时便能计算出系统的第一阶频率，使计算结果更符合真实情况。

另外，非连续基函数法和差分方法得到时间历程曲线，其幅值均是波动型的，体现了刚度非线性和摩擦的作用。

4结论

将刹车盘/摩擦块系统近似为循环梁结构，利用非连续基函数法计算摩擦块局部接触对系统模态及响应的影响。结论如下：

(1) 非连续基函数方法是通过将局部约束处简化成线性弹簧，通过估算合理的刚度值，得到约束作用下系统的基函数，作为传统模态方法的线性基函数的补充，可以更准确地描述局部约束下的系统模态振型。由于每一处局部约束只需计算第一阶非连续基函数，因此分析过程较为简单。

(2) 局部摩擦接触对循环结构的双模态特性会产生较大影响，某类模态会被抑制，抑制程度取决于约束的位置。

(3) 使用非连续基函数法计算系统响应，可以准确计算出波动型响应，因此可用於分析各类非线性系统动力学的研究。

进一步的工作，需要综合考虑刹车盘振动和制动块振动的联合方程，以及摩擦力的非线性和参数时变性因素，研究系统动力学降维和产生制动噪声的结构不稳定振动机理。

参 考 文 献

[1] 丁千，翟红梅.机械系统摩擦动力学研究进展[J].力学进展，2013，43(1): 112-131.

DING Qian, ZHAI Hong-mei. The advance in researches of friction dynamics in mechanics system[J]. Advances in Mechanics, 2013, 43 (1): 112-131.

[2] 余为高, 于学华. 应用有限元法对盘式制动器制动噪声分析[J].科学技术与工程，2009, 9(2): 3234-3236.

YU Wei-gao YU Xue-hua.Analysis of disc brake noise based on finite element methods[J].Science Technology and Engineering,2009,9(2);3234-3236.

[3] Hochlenert D, Hagedorn P. Control of disc brake squeal-modelling and experiments[J]. Structural Control and Health Monitoring, 2006, 13:260-276.

[4] Stanbridge A B, Ewins D J. Using a continuously-scanning laser doppler vibrometer for modal testing[C].Proc. IMAC, 14th Int. Modal Analysis Conf. 1996, 816-822.

[5] Fieldhouse J D, Newcomb T P. An experimentalinvestigation into disc brake noise[J]. Proc. IMechE, 1993,C444/036, 145-159.

[6] Cunefare K A, Ryan R. Investigation of discsqueal via sound intensity and laser vibrometry[J]. 2001, SAE Paper No. 2002-01-1604.

[7] Gianninia O, Massi F. Characterization of the high-frequency squeal on a laboratory brake setup[J]. Journal of Sound and Vibration, 2008, 310: 394-408.

[8] 吕延军,虞烈，刘恒. 非线性转子一轴承系统的动力学特性及稳定性[J].机械强度, 2004, 26(3)：242-246.

LÜ Yan-jun, YU Lie, LIU Heng.Dynamic characteristics and stability of nonlinear rotor-bearing system[J]. Journal of Mechanical Strength.2004.26(3):242-246.

[9] Segalman D J. Model reduction of systems with localized nonlinearities[J]. ASME Journal of Computational and Nonlinear Dynamics, 2007, 2: 249-266.

[10] Shin K, Brennan M J, Joe Y G, et al.Simple mode1s to investigate the effect of velocitydependent friction on the disk brake squeal noise[J]. Int. J.Automotive Technology, 2004,5(1):61-67.

[11] Joe Y G, Cha B G. Analysis of disc brake instability due to friction-induced vibration using a distributed parameter model[J]. International Journal of Automotive Technology, 2008, 9(2):161-171.

[12] Berger E J. Friction modeling for dynamic system simulation[J]. Trans ASME Appl Mech Rev, 2002, 55: 535-577.