含非线性边界梁结构频响特征的实验研究

第一作者 赵环迪 男，硕士生，1987年生

通信作者 陈力奋 女，博士，副教授，1966年生

邮箱：lfchen2@fudan.edu.cn

含非线性边界梁结构频响特征的实验研究

赵环迪，王珺，陈力奋

(复旦大学 力学与工程科学系，上海200433)

摘要：利用实验方法研究含非线性边界的梁结构频响特征。实验对象由一根矩形截面的主梁和二片与之垂直的片梁构成-T字型结构，通过在片梁两端垫放不同厚度的钢尺，使主梁的一端形成不同的几何非线性约束边界，片梁不同程度的预变形改变了主梁静平衡点的位置。实验结果发现，预变形和外激励幅值对系统的非线性频响特征影响显著，随着预变形和外激励幅值的变化，主梁的频响特征呈现出软特性、硬特性和线性特性之间复杂的演变过程。进一步的理论分析表明，预变形的存在使得系统的动力学控制方程同时含有平方和立方非线性，数值计算的结果与上述实验现象相吻合。实验研究和数值计算的结果，宏观上揭示了几何非线性约束边界中的预变形对梁结构频响特征的影响规律。

关键词：非线性边界；预变形；频响特征；实验研究

基金项目：国家自然科学基金资助项目(11172067)

收稿日期：2013-11-29修改稿收到日期：2014-02-20

中图分类号:O322文献标志码： A

Tests for frequency response features of a beam structure under nonlinear boundaries

ZHAOHuan-di,WANGJun,CHENLi-fen(Department of Mechanics and Engineering Science, Fudan University, Shanghai 200433, China)

Abstract:Tests for frequency response features of a beam structure under nonliear boundaries were conducted here. The test rig consisted of a linear cantilever main beam with a rectangular cross-section and two thin identical sheet beams connected at the main beam's free end and being perpendicular to the main beam to form a T-type structure. The different nonlinear supports at the one end of the main beam were formed by inserting steel rulers with different thicknesses into the ends of the sheet beams. The different pre-deformation levels of the sheet beams change the main beam’s equilibrium position. The test results showed that with the variation of pre-deformation and external excitation amplitude, the frequency response features of the main beam reveal a complex evolution process among soft characteristic, hard one and linear one. The further theoretical analysis showed that the pre-deformation makes the beam’s dynamic governing equations contain square and cubic nonliear terms. The results of numerical simulation agreed well with those of tests, they demonstrated that the pre-defoemation and external excitation amplitude have a significant effect on the beam’s frequency response features.

Key words: nonlinear boundary; pre-deformation; frequency response features; experimental study

非线性因素存在于大量的工程结构中，如接触碰撞中的间隙、干摩擦，材料弹塑性、构件大变形等，这些非线性因素的存在会使得结构在较小的动态载荷下产生线性系统所没有的现象，如分岔、混沌、超(次)谐波共振、频率漂移和跳跃现象等。为使系统和产品的动态设计、加工、运行和控制满足日益提高的运行速度和精度需求，需要深入分析非线性对系统动力学的影响。

工程结构中大量的连接件和边界是非线性的[1-3]，这些非线性元件除了受动态激励外，还常常受到其他载荷，如重力、装配缺陷等引起的预载，使得结构表现出非常复杂的的动态响应[4]，其中最为典型的频域特征是随着激励力的增加而产生“频率漂移”和“跳跃”现象。在复杂工况下，由过载引起的频漂将会导致非常严重的后果，已引起工程技术人员的重点关注。

梁结构在工程中有着广泛的运用，特别是细长梁，在受到外界激励时，容易发生大转动和大变形的非线性现象。近年来，非线性动力学理论和方法正从低维向高维乃至无穷维发展，其规模和难度不断提高，而实验研究同样具有重要的价值，可以从宏观上展示非线性现象的存在[5]。梁的非线性振动实验研究可以追溯到19世纪70年代，其中较有代表性的有Moon等[6]利用铁磁梁在两块磁铁间的运动，首次观察到了奇怪吸引子的存在，而后又发现了次谐波共振和混沌现象；采用带有质量块的L型梁结构，Haddow等[7-8]观察到了主共振激励下结构一二阶模态的非线性周期运动，通过参数的调节，发现了模态耦合现象，并首次验证了饱和现象的存在；陈予恕等[9]采用受纵向激励的梁结构对1/2亚谐分岔特性进行了实验研究，得出了整个参数平面上具有不同拓扑结构的分岔图；Fujino等[10]设计了三自由度的悬索梁结构，在观察到并验证了内共振和饱和现象的同时，还发现了长时间历程中双稳态现象的存在；近十年来，不断地有关于实验结果很好地验证了非线性理论的报道[11-13]。

梁结构的非线性实验研究成果对理论上发现的复杂动力学行为给出了直观的解释，为进一步探究实际结构的非线性振动本质，需进一步从物理或结构如对称性、密度分布、惯性力或预变形等出发，研究这些因素对结构非线性响应特征的影响规律。Royston等[14]进行了含有静载荷的局部非线性结构在周期激励下响应特征的实验和仿真研究，仿真结果表明由于静载荷的存在改变了系统的静平衡位置，从而产生不对称的非线性刚度，导致系统在一定的静载荷下首先呈现刚度的软特性，含非线性约束支撑的简支梁实验也验证了这一结论；冯志华等[15]通过对受轴向基础激励悬臂梁非线性动力学的建模和分析，表明梁的非线性惯性项具有软特性效应，而梁的非线性几何项具有硬特性效应；卫洪涛等研究了套筒连接结构非线性对梁频漂的影响，表明带预紧力时的间隙对梁频漂的影响呈现软-硬效果，这一现象与特定航天器结构的实验和分析结果一致；王珺等[16]研究了预变形对非线性结构响应特征的影响，数值计算结果显示出随着预变形的逐渐增大，非线性结构频响特征呈现从硬特性向软特性的转变，并求出了转变过程的临界变形；而随着外激励幅值的增大，则是从软特性向硬特性转变。上述研究成果多偏重于理论分析和仿真计算，较少见到利用实验方法研究物理或几何因素对结构非线性振动特性的影响。

针对含非线性边界梁结构的频响特征，主要利用实验方法研究了非线性约束中的预变形对主共振下梁的频响特性的影响。实验对象由一根矩形截面的主梁和二片与之垂直的片梁构成-T字型结构[17]，通过在片梁两端垫放不同厚度的钢尺，使主梁的一端形成不同的几何非线性约束边界。片梁不同程度的预变形改变了主梁静平衡点的位置，理论上使得系统的动力学控制方程同时含有平方和立方非线性。本实验研究和数值计算结果均表明，随着预变形和外激励幅值的变化，主梁的频响特征呈现出软、硬以及线性特性之间复杂的演变过程。

1实验装置及方法

1.1实验系统

实验系统由试件、实验平台、激振器、功放、数据控制采集系统、加速度和力传感器以及电荷放大器组成。试件为一矩形截面主梁，一端用压块固定，另一端与两片薄梁用一个M5的螺栓(12.9级内六角螺丝，配合弹簧垫圈和标准平垫圈使用)与自锁螺帽连接(见图1)。

图1　实验系统 Fig.1 Expeximental system

DP控制采集仪集成了Signalcalc430动态信号分析仪和Signalcalc550动态控制仪，功率放大器型号为YE5872，激振器最大激振力为200 N，满足实验要求，数据信号控制采集装置(见图2)。图3所示为实验系统结构示意图。这里采用的是力幅恒定的正弦扫频实验。

图2　数据信号控制采集装置 Fig.2 Setup of signal acquisition

图3　实验系统结构示意图 Fig.3 Schematic diagram of experimental system

1.2试件参数与测点布置

矩形截面的主梁经过先铸造后调质处理，使其强度、塑性和韧性得到很大程度的调整，具有良好的综合机械性能，两个片梁采用线切割加工而成，满足实验精度要求。试件的几何参数(见表1)。

表1　几何参数

本实验采用的是四通道的振动控制采集仪，其中一通道连接力传感器，其它三个通道连接加速度传感器，传感器放置的位置(见图4)。

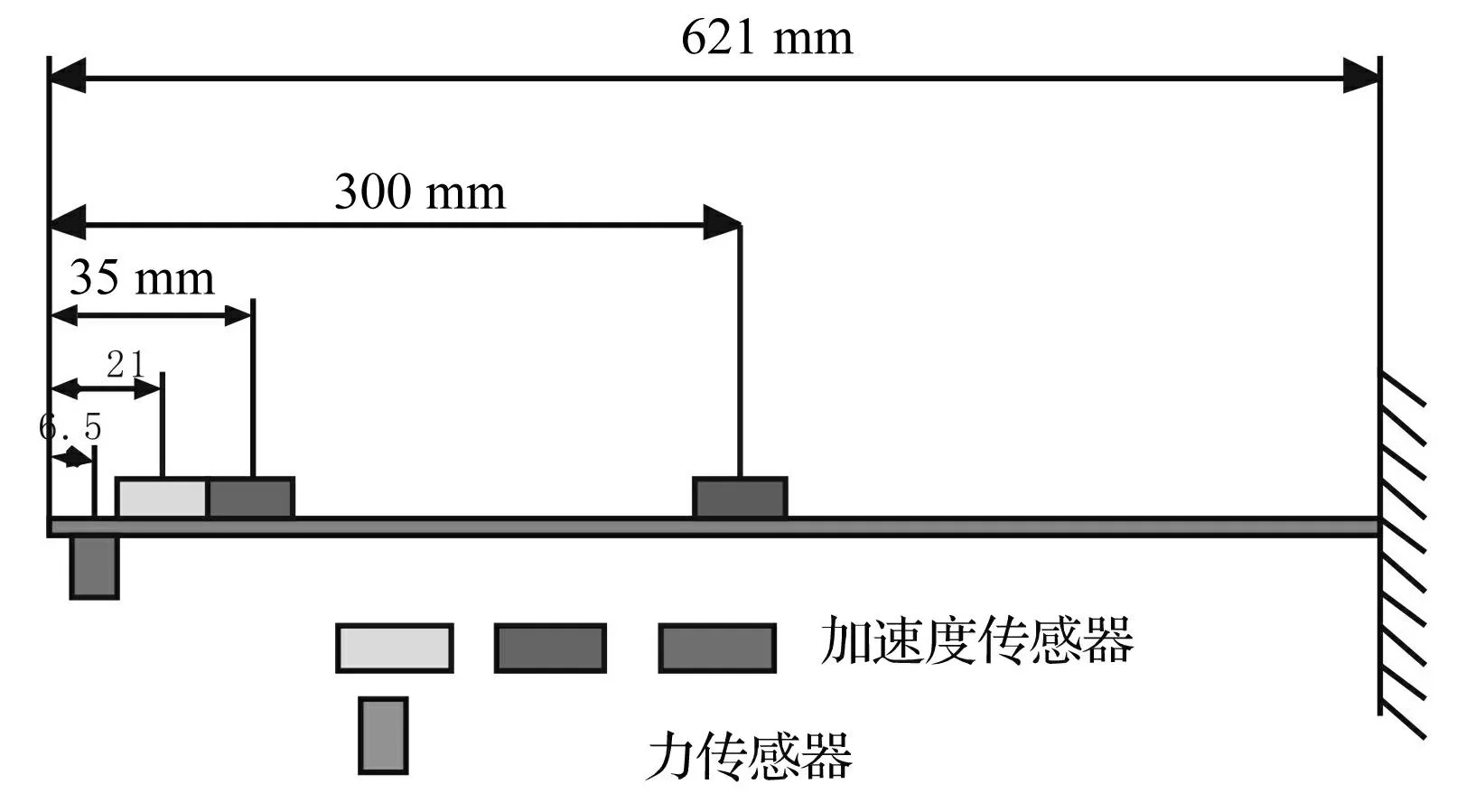
图4　实验测点位置 Fig.4 Observation location on the beam

1.3实验方法

主要通过改变预变形、激励力幅值的大小和不同的扫描方式，研究预变形对非线性结构频响特征的影响。主梁的静平衡位置使两片梁基本保持水平位置；(见图5(a))采用在片梁左右两端压块处逐一垫放厚度为0.7mm的钢尺，使片梁产生一定的弯曲静变形，(见图5(b))。

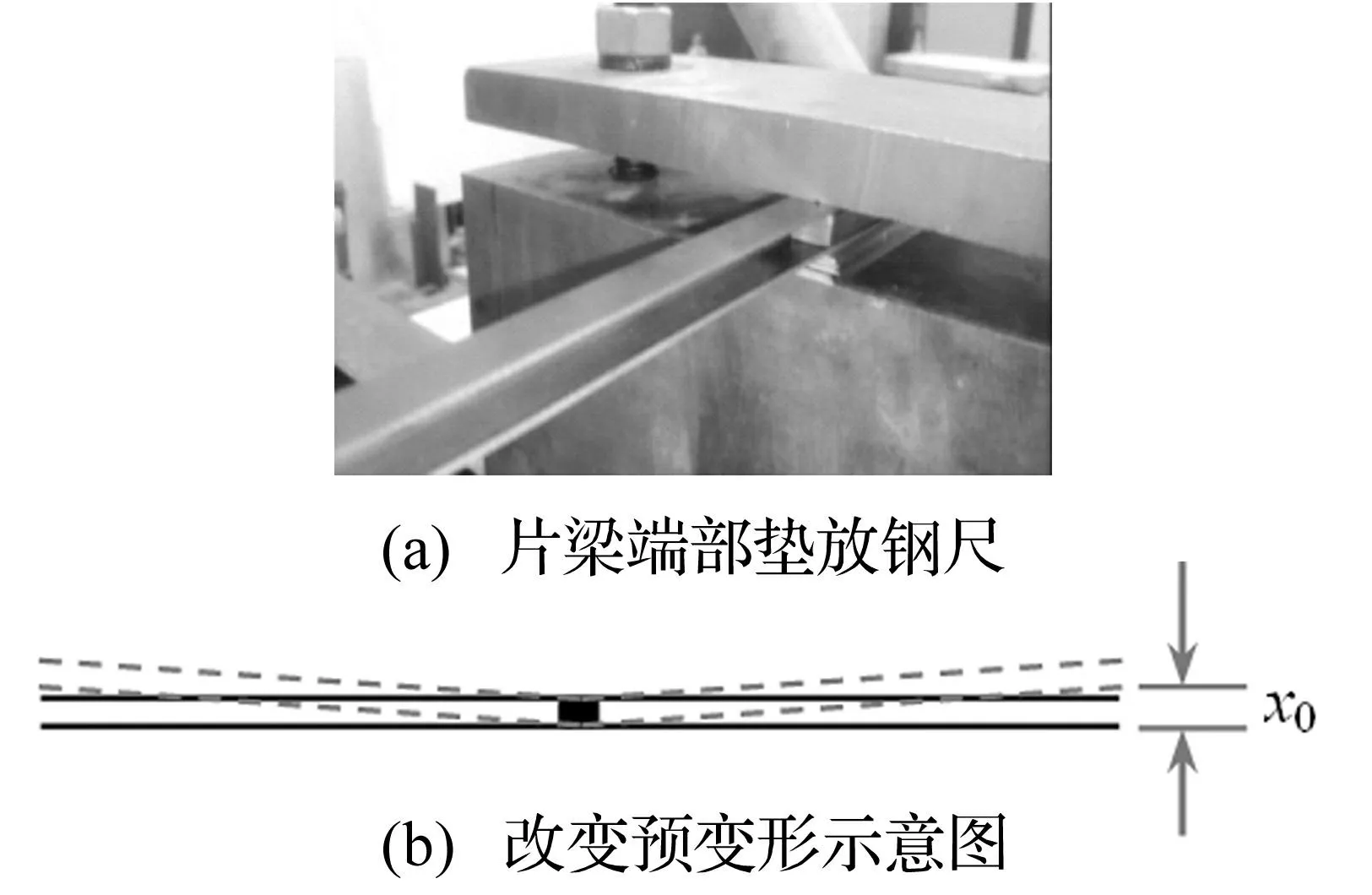
图5　改变预变形的实验方法 Fig.5 Experimental Study with different pre-deformation

对以下各种工况进行扫频实验：

(1) 垫放的钢尺厚度分别为： 0.0、0.7 mm、1.4 mm、2.1 mm、2.8 mm、3.5 mm、4.2 mm、4.9 mm、5.6 mm、6.3 mm和7 mm共十一个不同位置；

(2) 每个位置下，进行激励力幅值为0.05～2 N范围内力幅恒定的正弦扫频；

(3)每种工况下，进行从低到高和从高到低的扫频实验，扫描方式为线性扫频，频率间隔为0.1Hz/s。

实验中发现，在相同实验条件下，不垫钢尺(0.0 mm处)和垫2片钢尺(1.4 mm处)的频响曲线差异较小；而在垫1片钢尺(0.7 mm处)时的峰值位置频率最低，由此可以判定系统的动平衡点在0.7 mm位置附近。将动静平衡点的位移差定义为结构的预变形x0，(见图5(b))。由此可知，实验中的十一个不同位置分别对应的预变形为：

x0=-0.7 /0.0 /0.7 /1.4 /2.1 /2.8

/3.5 /4.2 /4.9 /5.6 /6.3(单位：mm)

2实验结果及分析

由于三个加速度传感器采集的信号所显示的第一阶固有频率均相同，所以以下均采用端点处位移频响数据。

针对分别给定的十一个预变形位置，T字型梁结构第一阶固有频率附近处的位移频响曲线随激励力幅值的变化过程(见图6)，其中包括图6(a)从低到高；图6(b)从高到低的两种扫频方式。

当激励力幅值较小(F≤1.0 N)时，位移频响相对稳定，记录结构峰值位置的频率点，则可得结构一阶固有频率值随预变形和外激励幅值的变化规律(见图7)。

从图6和图7可知，随着预变形大小的变化，结构的频响特征有下述特点：

(1) 预变形x0接近于零时，结构的一阶固有频率值基本随外激励幅值的增加而增大，如图6的(1)、(2)和(3)所示，位移频响总体呈硬弹簧特征；

(2) 预变形x0=±0.7 mm时，尽管外激励幅值的分布不同，但结构的频响振动特性非常接近，尤其是在较小的外激励幅值下(见图7)，表明预变形的正负对结构振动特征影响较小；

(3) 当预变形x0=3.5 mm时，结构的一阶固有频率值随外激励幅值的增加而减小(见图6的(7))，位移频响总体呈软弹簧特征。

取激励力幅值F=0.5N时的实测数据，对不同预变形下结构的位移频响曲线进行了比较(见图8)。不难发现，对于相同的外激励幅值，由于预变形的不同，主梁结构呈现软、硬以及线性等完全不同的刚度特性。

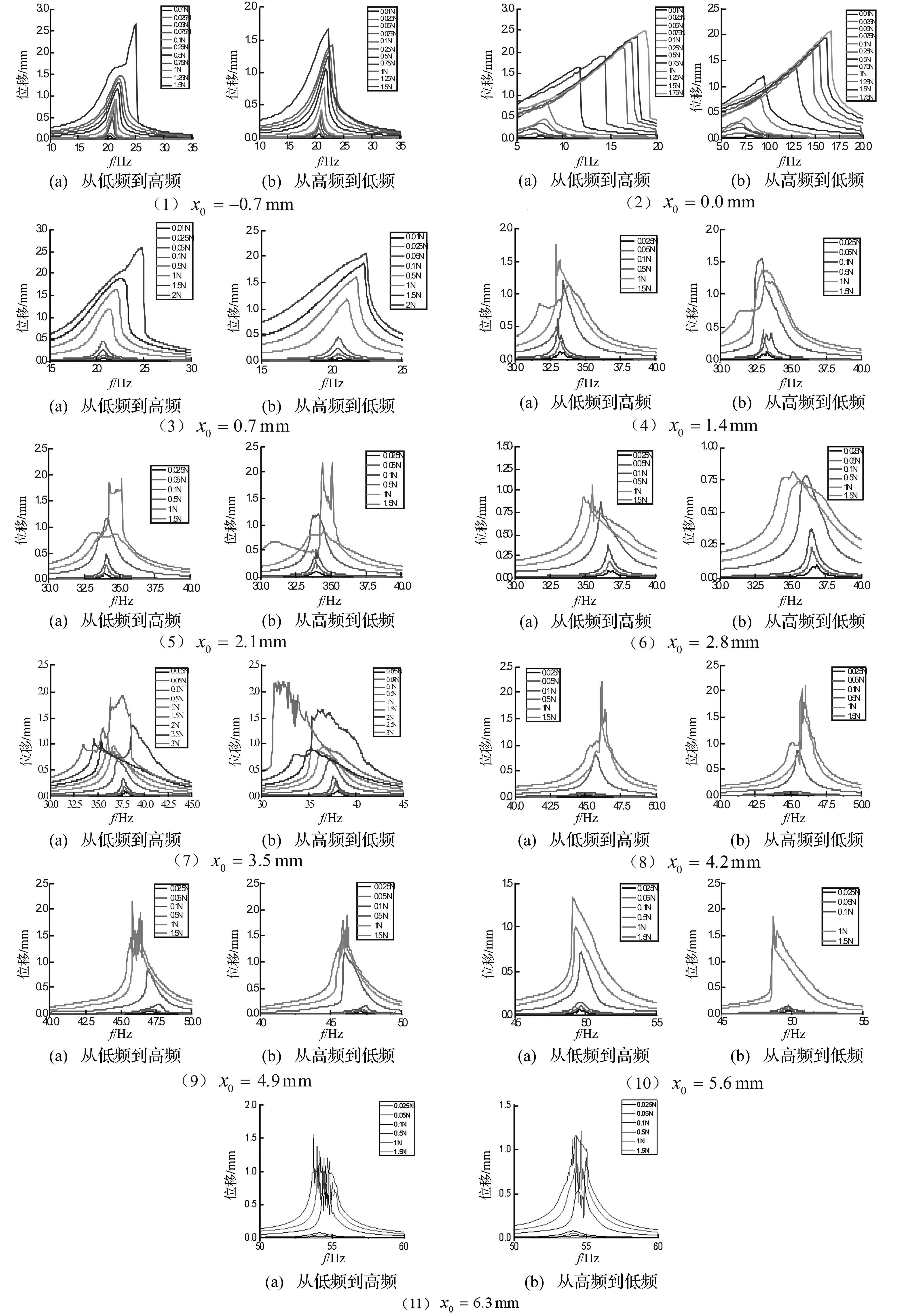
图6　不同预变形位置处，位移频响随激励力幅值的变化过程 Fig.6 Frequency response of structure with different pre-deformation

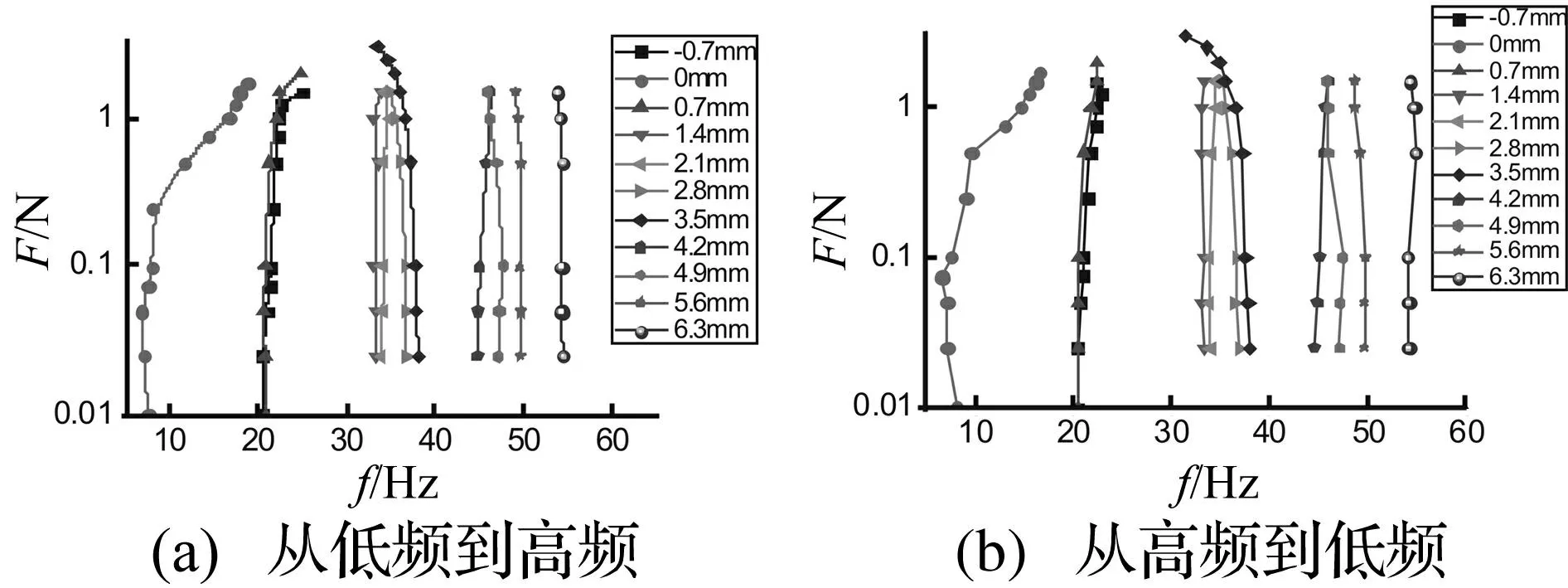
图7　同一预变形位置下，激励力与一阶固有频率的关系 Fig.7 Relation between excitation force and natural frequency (with same pre-deformation)

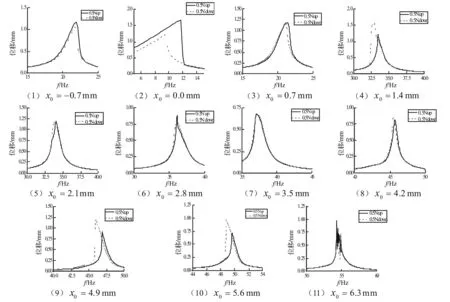
图8　激励力幅值F=0.5 N时不同预变形下结构频响特征比较 Fig.8 FRF comparison with different pre-deformation under excitation power F=0.5 N

3含预变形结构的数值分析

实验研究结果表明，预变形导致含非线性边界梁结构的频响特征呈现出软、硬特性和线性之间复杂的演变过程。为进一步阐明预变形的影响机理，本节进行理论分析和数值计算。

考虑图9所示的单自由度质量-阻尼-弹簧系统，设弹簧大变形产生的非线性模型为：

F=-kx-k*x3

(1)

式中：k为线性刚度系数，k*为立方刚度系数；负号表示力的方向与变形x方向相反。

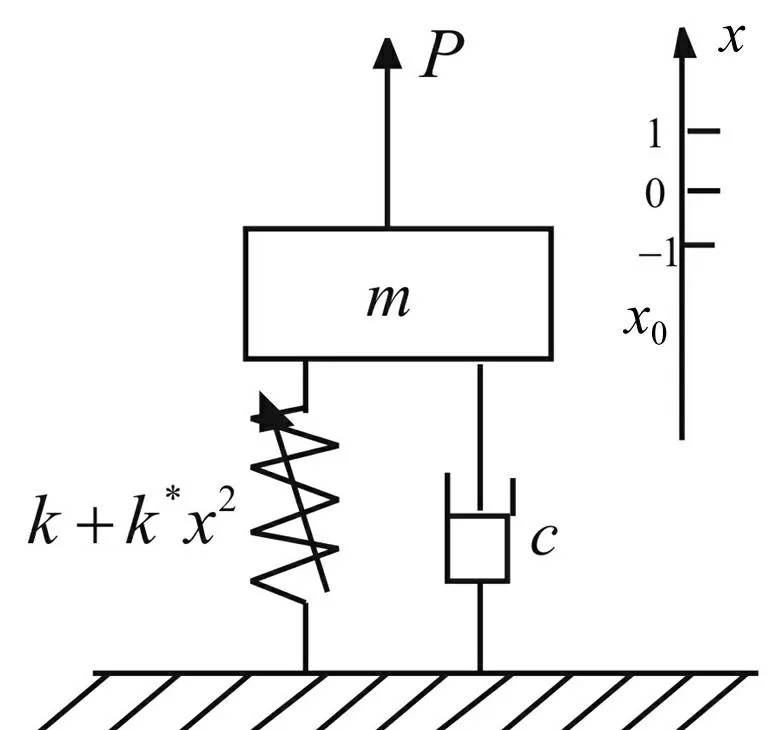
图9　含非线性弹簧的单自由度质量—阻尼—弹簧系统 Fig.9 1-degree-of-freedom spring-damper system with nonlinear spring

考虑矩形截面主梁承受预载荷，则静平衡状态时弹簧存在预变形x0，此时弹簧对m的作用力为：

(2)

当m相对静平衡位置产生相对位移Δx时，弹簧作用力的增量为：

3k*x0Δxx2-k*Δxx3

(3)

3k*x0Δxx2+k*Δxx3=P(t)

(4)

可知，结构的线性频率为(Hz)：

(5)

显然与预变形x0相关。

当预变形x0=0时，结构刚度为立方非线性，当k*>0时将呈现刚度的硬特性；当存在预变形即x0≠0时，Δxx的二次项系数非零，随着Δxx的增加，无论k*正负都将首先体现刚度的软特性[18]。

预变形x0的计算范围为0～10 mm，采样间隔Δxx0=0.1 mm；计算中激励力幅值F的变化范围为2～16 N，采样间隔ΔxF=0.1 N；计算扫频范围f为20～120 Hz，递归细分时设定间隔下限Δxfmin=0.1Hz。

由此，在给定的范围内，得到了全参数域上含几何非线性单自由度结构的频响特征随预变形和外激励幅值的变化规律。图10给出了当外激励力幅值F=14 N时，扫频过程中的跳跃点[16]位置随预变形的变化规律。从中不难发现，随着预变形的不断加大，结构由硬特性(不稳定频段逐步变窄)转化为软特性(不稳定频段由窄变宽再变窄)；在一定的预变形位置(图10中x0约在4.0～6.0 mm)处，频响特性处于软硬特性的转变过程。

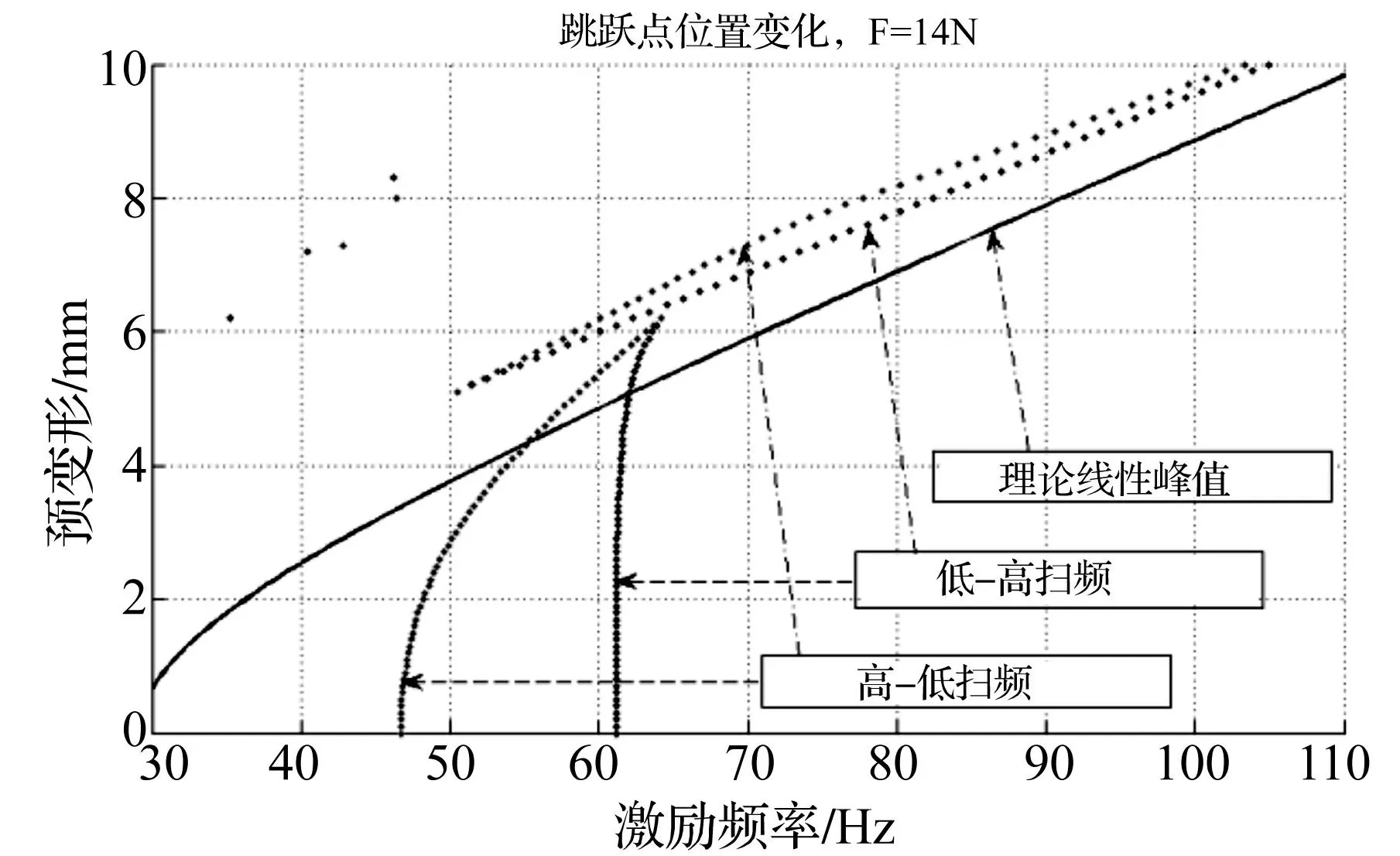
图10　跳跃点位置随预变形的变化(F=14 N) Fig.10 The jump point with the pre-deformation while F=14 N

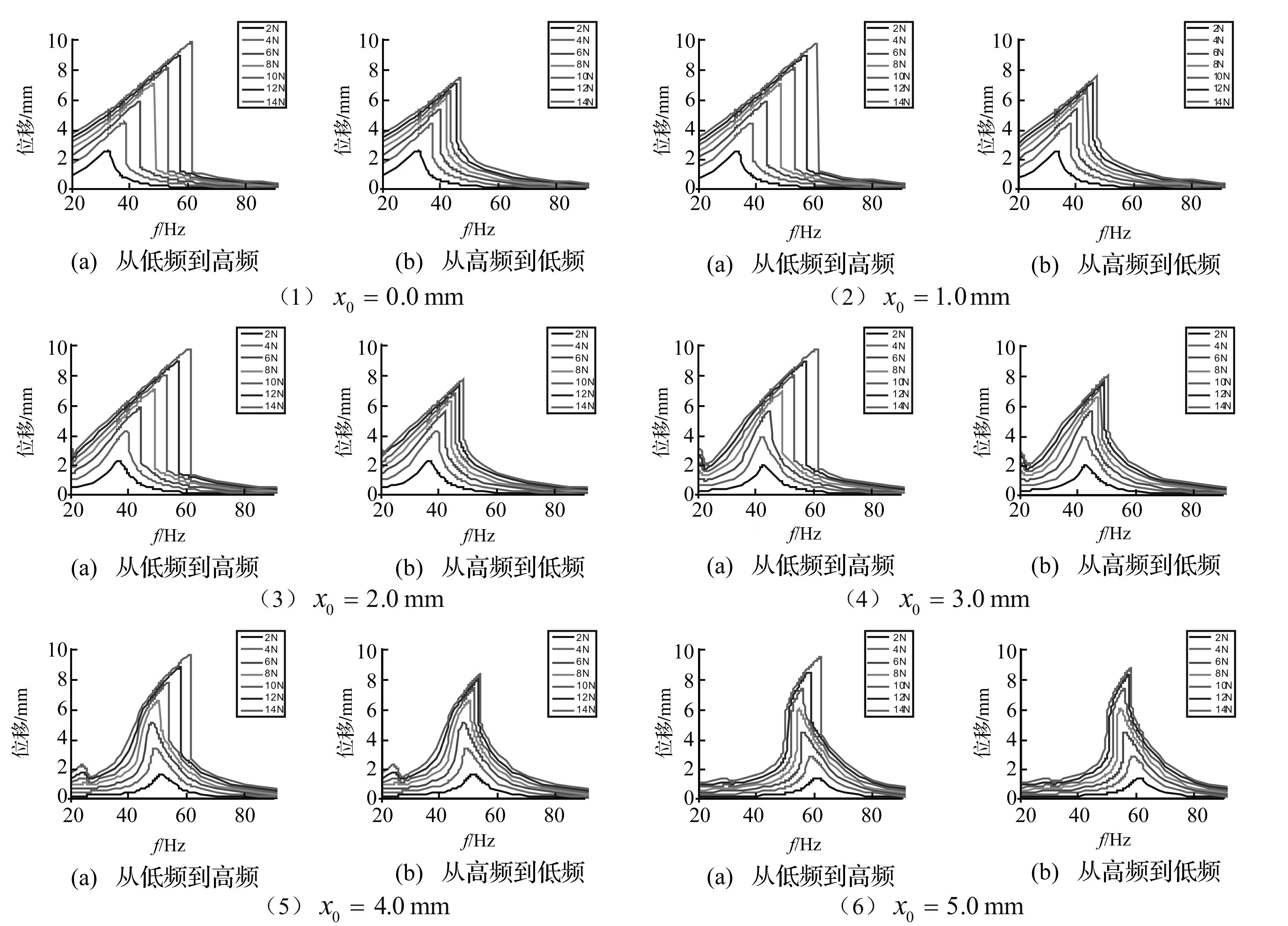
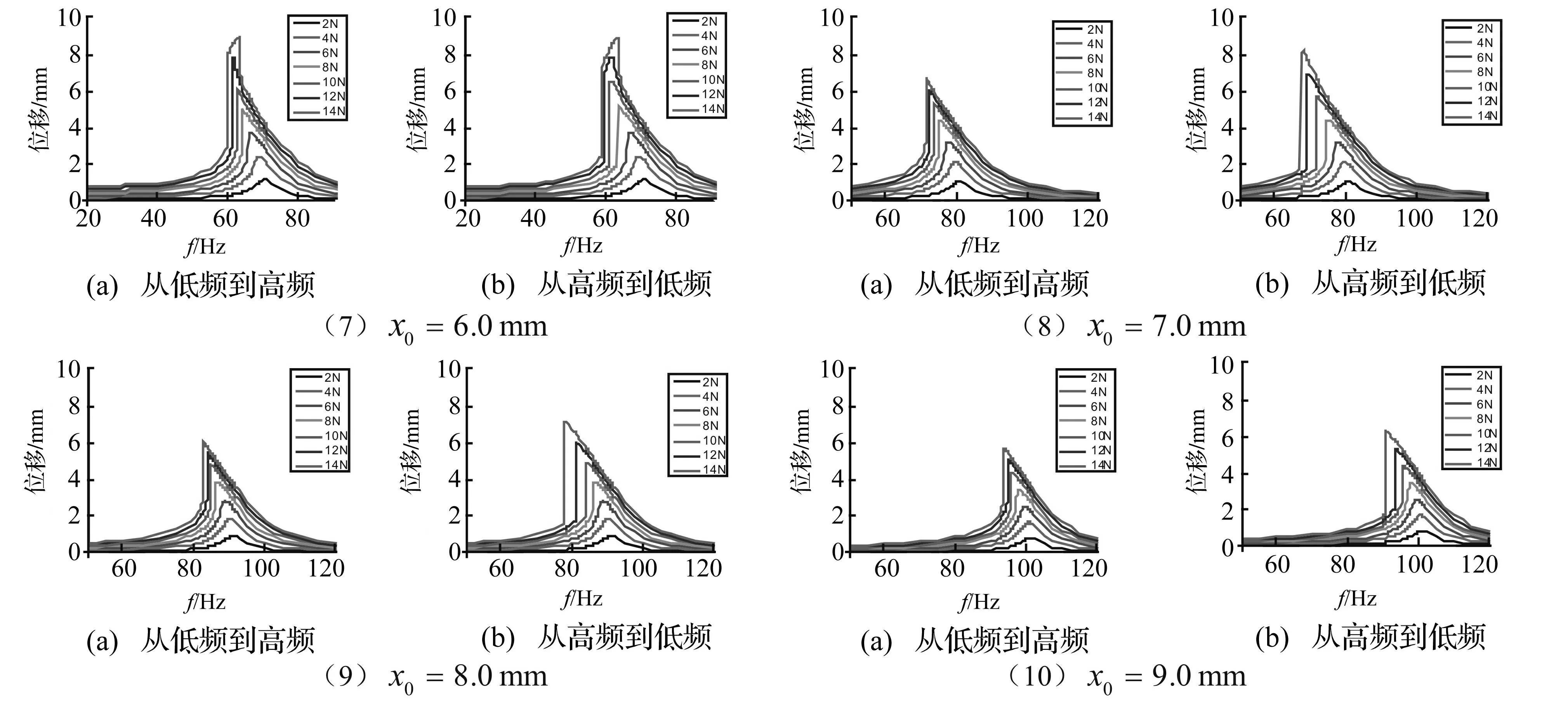
图11　不同预变形位置处，位移频响随激励力幅值变化的计算结果 Fig.11 Calculated frequency response of 1DOF structure with different pre-deformation

为体现结构频响特征的演变过程，以下给出十个预变形位置：

x0=0.0 /1.0 /2.0 /3.0/4.0

/5.0 /6.0 /7.0/8.0/9.0(单位：mm)

结构固有频率附近处的位移频响曲线随激励力幅值的变化过程(见图11)，其中包括：图11(a)从低到高；图11(b)从高到低的两种模拟扫频计算结果。固有频率随预变形和外激励幅值的变化规律(见图12)。

图12　固有频率随激励力幅值变化的计算结果 Fig.12 Relation between excitation force and natural frequency (Calculated)

由图11和图12可知，随着预变形大小的变化，结构的频响特征有下述特点：

(1) 预变形较小时，结构的固有频率基本随外激励幅值的增加而增大，如图11的(1)～(3)所示，位移频响总体呈硬弹簧特征；

(2) 在一定的预变形下，当外激励幅值较小时结构开始出现软弹簧特征，而随着激励力幅值的增加又转而呈现硬特性，如图11的(4)～(7)所示；其中还会产生超谐波共振的非线性现象。

(3) 当预变形较大时，在所计算外激励幅值范围内，结构的位移频响总体呈软弹簧特征。

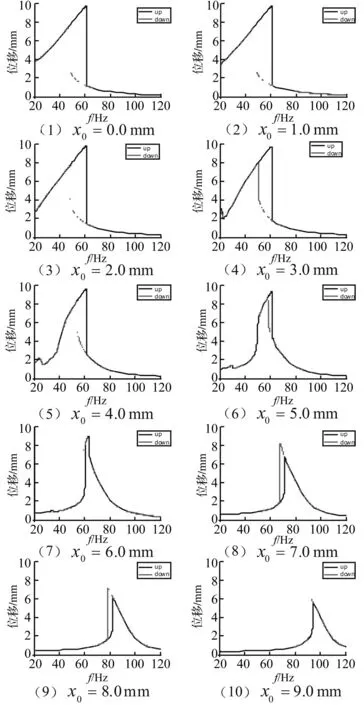
图13　激励力幅值F=14 N时 不同预变形下结构频响特征比较 Fig.13 FRF comparison with different pre-deformation under excitation power F=14 N (Calculated)

为进一步说明上述频响特征，提取激励力幅值F=14 N时的计算数据，对上述十个预变形下结构的位移频响曲线进行了比较(见图13)。

4结论

主要用实验方法研究了非线性边界约束中的预变形对梁结构频响特征的影响。结果表明：

(1) 预变形接近于零时位移频响总体呈硬弹簧特征；

(2) 预变形的正负对结构频响特征影响较小；

(3) 当结构存在预变形时，位移频响随外激励幅值的变化，总体呈先软后硬的刚度特征；

(4) 在同样大小的外激励幅值下，随着预变形的增加，主梁结构则呈现先硬后软完全不同的刚度特性。数值计算结果也印证了上述结论的合理性。

从实验和数值计算结果可以发现，预变形导致主梁结构产生明显的“跳跃”和“频率漂移”现象，且软、硬刚度特性在同样的外激励幅值下均有可能。数值计算结果进一步可以发现更为丰富的非线性现象，如超谐波共振。本研究结果从宏观上揭示了几何非线性约束边界中的预变形对梁结构频响特征的影响规律。

由于数值计算采用的是单自由度系统，计算结果仅从定性上说明实验现象的合理性。这里以主共振下频域响应为主要研究对象，时域响应特征的研究成果将另文发表。

参 考 文 献

[1] Dhupia J S, Powalka B, Ulsoy A G, et al. Effect of a nonlinear joint on the dynamic performance of a machine tool[J]. Journal of Manufacturing Science and Engineering, 2007, 129(5): 943-950.

[2] 卫洪涛，孔宪仁，王本利,等. 套筒连接结构非线性对梁频漂的影响[J]. 振动工程学报，2012, 25(4): 373-379.

WEI Hong-tao, KONG Xian-ren, WANG Ben-li, et al. Effects of nonlinearities of sleeve joint on the frequency shift of a beam[J]. Journal of Vibration Engineering, 2012, 25(4): 373-379.

[3] Brake M R, Wickert J A. Modal analysis of a continuous gyroscopic second-order system with nonlinear constraints[J]. Journal of Sound and Vibration, 2010，329: 893-911.

[4] Ozturk E, Kumar U, Turner S, et al. Investigation of spindle bearing preload on dynamics and stability limit in milling[J]. CIRP Annals-Manufacturing Technology, 2012, 61: 343-346.

[5] 陈予恕，季进臣.非线性振动系统动力学行为的实验研究[J].力学进展，1996, 26(4): 473-481.

CHEN Yu-shu, JI Jin-chen. The experimental studies of dynamical behavior of nonlinear oscillating systems[J]. Advanced in Mechanics, 1996, 26(4): 473-481.

[6] Moon F C, Shaw S W. Chaotic vibrations of a beam with non-linear boundary conditions[J]. International Journal of Non-Linear Mechanics, 1983, 18(6): 465-477.

[7] Haddow A G, Barr A D S, Mook D T. Theoretical and experimental study of modal interaction in a two-degree-of-freedom structure[J]. Journal of Sound and Vibration, 1984, 97(3): 451-473.

[8] Balachandran B, Nayfeh A H. Observation of modal interactions in resonantly forced beam-mass structures[J]. Nonlinear Dynamics, 1991, 2: 77-117.

[9] 陈予恕，叶敏，詹凯君.非线性Mathieu方程1/2亚谐分岔的实验研究[J].应用力学学报，1990, 7(4): 11-16.

CHEN Yu-shu, YE Min, ZHAN Kai-jun. An experiment investigation of 1/2 subharmonic bifurcation solution of nonlinear Mathieu equation[J]. Chinese Journal of Applied Mechanics, 1990, 7(4): 11-16.

[10] Fujino Y, Warnitchai P, Pacheco B M. An experimental and analytical study of autoparametric resonance in a 3DOF model of cable-stayed-beam[J]. Nonlinear Dynamics, 1993, 4: 111-138.

[11] Emam S A, Nayfeh A H. Nonlinear responses of buckled beams to subharmonic-resonance excitations[J]. Nonlinear Dynamics, 2004, 35: 105-122.

[12] Lee Y Y, Su R K L, Ng C F, et al. The effect of modal energy transfer on the sound radiation and vibration of a curved panel: theory and experiment[J]. Journal of Sound and Vibration, 2009, 324: 1003-1015.

[13] 曾志刚，叶敏. 黏弹性复合材料屈曲梁非线性参数振动的稳定性和分岔分析[J]. 振动与冲击，2012, 31(2): 129-135.

ZENG Zhi-gang, YE Min. Stability and bifurcation of a parametrically excited viscoelastic composite buckled beam[J]. Journal of Vibration and Shock, 2012, 31(2): 129-135.

[14] Royston T J, Singh R. Experimental study of a mechanical system containing a local continuous stiffness non-linearity under periodic excitation and a static load[J]. Journal of Sound and Vibration, 1996, 198(3): 279-298.

[15] 冯志华，胡海岩. 受轴向基础激励悬臂梁非线性动力学建模及周期振动[J]. 固体力学学报，2002，23(4): 373-379.

FENG Zhi-hua, HU Hai-yan. Nonlinear dynamic modeling and periodic vibration of a cantilever beam subjected to axial movement of basement[J]. Acta Mechanica Solida Sinica, 2002，23(4): 373-379.

WANG Jun, ZHAO Huan-di, CHEN Li-fen. Effects of the initial deformation on the dynamic response of local nonlinear systems[J]. Journal of Dynamics and Control, 2014.

[17] Arslan O, Aykan M, Ozguven H N. Parametric identification of structural nonlinearities from measured frequency response data[J]. Mechanical Systems and Signal Processing, 2011, 25:1112-1125.

[18] Nayfeh A H, Mook D T. Nonlinear Oscillations[M]. New York: John Wiley & Sons, 1979.