重推国债期货对利率市场波动性的影响研究

重推国债期货对利率市场波动性的影响研究

夏秀相，侯擎天，周敦辉

(安徽财经大学 金融学院，安徽 蚌埠233000)

摘要：选择“2013年9月6日至2014年4月11日国债期货数据”和“2013年1月4日至2014年4月11日国债指数”数据，对国债期货推出设立虚拟变量，建立GARCH、GJR等模型定量分析了国债期货发挥的作用，得出了在引入国债期货交易之后,国债现货市场中信息的“负杠杆效应”有所改善，投资者由非理性趋向理性，国债现货市场中的市场风险有效地降低，但国债期货对国债现货市场波动性的影响十分有限等结论，并结合中国国债市场实际情况分析解释了重推国债期货后市场上信息的传递速度变慢这一与理论不符的结果，证明了国债期货合约的功能发挥有助于市场形成完善的基准收益率体系并有助于有效规避利率风险。

关键词：国债期货；国债现货；GARCH模型；GJR模型

作者简介：夏秀相，学生，安徽财经大学。

基金项目：安徽财经大学2014年度大学生科研创新

文章编号：1672-6758(2015)02-0058-4

中图分类号：F832.5

1引言

国际上，一些知名学者从不同角度研究国债期货的功能发挥。Grinblatt和Jegadeesh(1996)[1]认为国债期货定价效率主要取决于保证金交易制度。在对冲风险绩效的研究中，Figlewski(1984)[2]等提出了由回归可以获得最优对冲比例，Johansen(1988)[3]提出了解决伪回归风险的协整检验。在国内，袁东(2003)[4]，党剑(2002)[5]，贺强和辛洪涛(2012)[6]等研究表明国债期货可以规避债券市场风险，从而推进我国利率市场化进程。另有一些人探讨了我国是否应该重推国债期货，认为重推国债期货的条件已趋于成熟。这些研究多是关于国债的诸多功能,是在国债期货推出之前进行的，并且只是定性地分析国债期货与利率市场的关系，没有定量分析国债期货的推出对国债现货市场的影响。

正是由于利率的波动，国债期货才有推出的必要，因为国债期货的基本功能就是规避利率风险。市场利率的变化可以直接由国债期货反映，如果央行规定存贷款利率，那么出台的货币政策将会很大程度上影响国债期货价格。利率水平主要反映了经济发展对货币的需求程度，经济发展得过快往往导致利率上升。因此，利率因素是影响国债期货价格波动的最核心因素，所以本文着眼于国债期货推出后，对利率市场波动性的影响进行研究。

2数据选取、处理和分析

根据国债利率充当基准利率的客观机理，而国债利率又反映在国债现货的价格波动中，因此用国债现货价格指数来充当最佳基准利率，从而通过分析推出国债期货对现货价格波动的影响，进而分析得到重推国债期货对利率市场波动性的影响。

选取中国金融期货交易所2013年9月6日至2014年4月11日代码为TF1406的142个五年期国债期货数据，选取了2013年1月4日至2014年4月11日304个国债指数数据，并将其分为2013年9月6日之前的162个数据，和之后的142个数据。

国债现货价格的收益率能够反映其变动程度,收益率的方差体现了市场的波动特征以及风险特征。用取对数作差分形式对日收益率数据进行相应的处理，计算公式为:

Rt=ln(Pt/Pt-1)

其中Rt为t时刻样本的收益率，Pt、Pt-1分别为t时刻、t-1时刻样本的收盘价，并对序列通过减去均值作中心化处理，得到相应的新序列(以下均用此新序列建模)。

首先,绘制整个样本期间内(20013年1月4日至2014年4月11日)国债指数日收益率数据的折线图，发现该序列具有较明显的波动“集聚”现象,说明误差项可能具有条件异方差的性质。

其次,整个样本期间内(2013年1月4日至2014年4月11日)国债指数日收益率数据国债指数日收益率序列的偏度为0.291618、峰度为36.91593。由此我们知道本序列具有典型的尖峰、厚尾特征。

最后,平稳性检验。利用ADF检验法，对国债指数的日收益率序列以及国债期货的日收益率序列进行单位根检验,发现在国债期货推出前、后和在整个样本区间内,国债指数的收益率序列和国债期货的日收益率序列都具有平稳性。

3GARCH建模

3.1 ARCH 建模。

第一步,分别对序列进行滞后1、2、3、4、5阶的自回归分析,根据AIC准则和Schwarz准则,对国债指数的日收益率序列进行自回归分析,发现滞后阶数为3阶的AIC的值和SC的值都是最小的，因此选择较合适的滞后三阶模型,即:

Rt=φ1Rt-1+φ2Rt-2+φ3Rt-3+μt

第二步,对拟合后的残差作滞后8阶的自相关检验。经检验,发现残差序列中，所有自相关系数和偏自相关系数都位于虚线之间,并且Q统计量对应的概率值均大于0.05，因此，认为在显著性水平为5%的条件下，残差序列不存在自相关。

第三步,再对残差序列进行滞后25期的ARCH-LM检验,发现在给定1%的显著性水平下,F统计量和nR2统计量相伴的概率值分别为0.002188,0.003053，都小于0.01，表明残差序列具有高阶的ARCH效应,因此选择GARCH模型重新进行建模。

3.2 GARCH模型参数估计。

在整个样本区间内(2013年1月4日至2014年4月11日)构建GARCH模型,并且我们引入一个虚拟变量XD,以此来修正GARCH模型。此时模型形式变为

式中,虚拟变量的赋值可以反映序列的时间特征，λ可以反映波动性,若显著,表明推出国债期货对现货市场的波动性的确产生了影响。若λ>0,说明国债期货交易加剧了现货市场波动；若λ<0,则国债期货交易减小了现货市场的波动；如果λ=0,表明现货市场的波动性并没有改变。

分别建立GARCH (1,1)模型、GARCH (1,2)模型、GARCH (2, 1)模型、GARCH (2,2)模型，比较拟合效果,通过AIC值和SC值,得出GARCH (1,2)模型最为优良,建立相应的GARCH方程。参数估计的结果如表1。

根据表1的结果可知，拟合的GARCH (1,2)方程为:

从模型的约束条件来看α1=0.041177>0，β1=1.515004>0，β2=-0.656149<0，显著性水平较高，并且α1+β1+β2<1,符合GARCH模型中参数的约束条件。根据模型的结果，可以看到，λ为负值,相应的概率值为0.0001,通过了显著性检验,表明推出国债期货降低了现货市场的波动性。另外,XD的系数很小,说明国债期货的影响相当有限。

再进行GARCH建模,并对拟合的残差序列进行滞后25期的ARCH-LM检验,发现在拟合的GARCH (1,2)模型,F统计量和相应的概率值分别为0.8229,0.8222，大于显著性水平5%,说明残差里包含的信息已经提取干净,残差序列已经不再有ARCH效应了。这反映GARCH(1,2)模型消除了条件异方差性,对国债指数的日收益率序列拟合得较充分。

4扩展的GJR(1,2)模型

考虑到在国债市场上,利好消息和利空消息对国债价格存在非对称性的冲击,因此，采用带虚拟变量GJR(1,2)模型，对不同信息反应的“杠杆效应”进行研究。模型如下:

在整个样本区间内(2013年1月4日至2014年4月11日)构建国债指数日收益率序列的GJR (1,2)模型,得到相应的参数估计结果如表2。

由表2可知,拟合的GJR (1,2)方程为:

表2　GJR (1, 2)模型的回归结果

根据模型拟合的结果可知,系数α1,β1,β2，均满足模型的约束条件,同时,在GJR(1,2)模型中λ也为负值,统计性质显著,表明推出国债期货的确降低了国债现货市场的波动。而XD的系数也很小,说明影响同样是很有限的。

5结论分析

分别对国债期货推出前、后建模并进行相关分析,得到相应的GARCH模型,同时添加虚拟变量修正GARCH模型,在整个样本区间内，研究推出国债期货对现货市场波动性的影响,并运用非对称的GJR(1,2)模型,验证GARCH的结果，得到如下信息：

5.1推出国债期货对市场传递信息速度的影响。

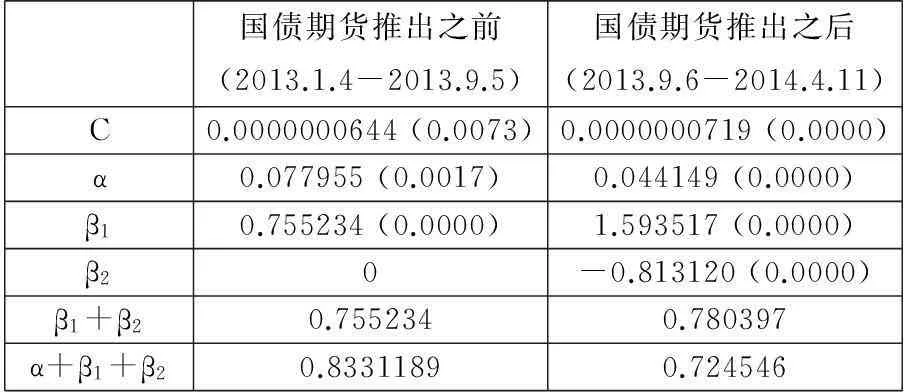
表3　GARCH模型条件方差方程的参数估计结果

由表3可知,推出国债期货之前,α的值为0.077955,而在国债期货推出之后,其值减小为0.044149,二者相差0.033806，说明上一期的市场信息对本期条件方差的影响程度有所减小；另一方面,在国债期货推出之前,对国债指数拟合的GARCH模型中的β1+β2值为0.755234,比国债期货推出之后对应的持续参数值0.780397小了0.025736,意味着国债现货市场中的旧信息对市场波动性的冲击稍稍增加。综合α和β的值,可以得出国债市场推出国债期货交易后,市场信息的传递速度却减慢了，并且从数据上看只是微小的影响。经过分析,认为造成这种现象的原因主要是：在我国国债市场中,由于推出国债期货不久,市场的双边交易才刚刚开始,长期累积的利空消息通常有集中释放的过程,这期间国债现货会受到旧信息的更大影响,导致在现货市场上降低了信息的流动速度。当旧消息的影响完全释放后,才会逐渐表现出国债期货对新信息的敏感性。

5.2推出国债期货对现货市场“杠杆效应”的影响。

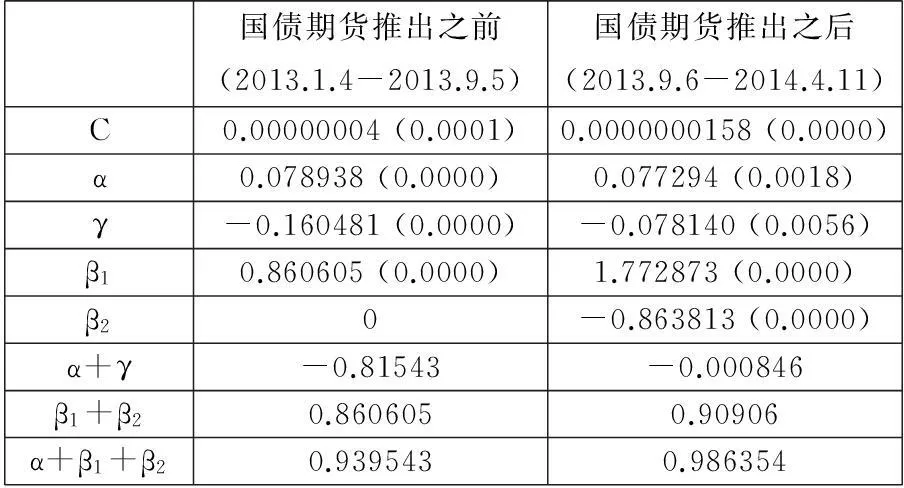
表4　GJR(1,2)模型条件方差方程的参数估计结果

通过不对称的GJR(1,2)模型,利用国债期货推出前、后这两个时间段的样本数据,探究国债期货上市以后对我国国债现货市场中信息“杠杆效应”的影响及影响程度。GJR(1,2)模型条件方差方程的参数估计结果如表4。

从表4可以看出,GJR(1,2)模型中的参数β1+β2在国债期货推出之前的值为0.860605,而在推出国债期货后其值增大为0.90906,表明旧信息对国债现货市场波动性冲击的程度增强了,这与GARCH模型中得到的结论一致，另一方面可以表明市场波动的新信息吸收在减弱。在GJR模型中,γ≠0系数，且通过显著性检验,表明在国债现货市场中，波动性是非对称的。γ<0,说明利好消息比利坏消息波动更大。在国债期货引入之前,当出现利好消息时,μt-1>0,则dt-1=0,会带给国债现货市场一个α=0.078938倍的冲击；当出现利空消息时,μt-1<0,此时，dt-1=1,则利空消息将产生一个α+γ=-0.81543倍的冲击。由此表明我国国债市场的投资者是趋于非理性的，存在一种从众心理。在国债期货引入之后,出现利好消息时,会带来一个α=0.077294倍的冲击,而出现利坏消息时,则会带来一个α+γ=-0.000846倍的冲击。由二者绝对值显著小于1可以看出，推出国债期货后,利好消息和利空消息对我国国债现货市场波动性产生的冲击均有所下降。反映信息冲击非对称效应的参数γ的绝对值在推出国债期货后显著降低,表明国债期货上市后国债现货市场中信息的“负杠杆效应”有所改善，投资者由非理性趋向理性。

5.3推出国债期货对现货市场波动性的影响。

无论是从GARCH (1,2)模型还是从GJR(1,2)模型中,都可看出条件方差方程中β1+β2的值远大于α的值,表明相对于新信息,旧信息对市场波动性的影响程度要大得多,说明导致我国国债现货市场波动性的主要原因不是推出了国债期货。

总地看来,GARCH模型中,在推出国债期货之前,(α+β1+β2)值为0.8331189,而在引入国债期货之后,其值降为0.724546,一定程度上表明了推出国债期货有效地降低了现货市场中的市场风险。在GJR模型中,得到了同样的结论。

从虚拟变量的系数中可以看到,无论是GARCH模型还是GJR模型,XD的系数都是负的,且通过了显著性检验,表明国债期货的确降低了现货市场的波动性。然而结果显示,XD的系数很小,表明国债期货对现货市场波动性的影响是很有限的。这样，可以认为，国债期货推出之后,在有限程度上抑制了现货市场的波动性，使得国债价格和价值更加趋于一致。但是，由于国债期货市场规模不大,其对国债市场的影响必然有限。

6结语

本文通过对国债期货上市前后国债现货市场情况的研究，说明了推出国债期货的确降低了我国利率市场的波动性。另一方面,由于GARCH模型中XD的系数非常小,表明国债期货对我国利率市场波动性的影响比较小。GJR-GARC(1,2)模型中参数γ<0，表明中国国债现货市场中利好消息的冲击大于利坏消息，即存在非对称效应，说明投资者是非理性的。随着我国金融改革的不断推进，金融市场的不断发展，可以预期国债期货将对现货产生更多的相互作用，对利率市场的影响也将更大。所以，尽管国债期货合约暂时没有充分发挥对利率市场的稳定功能，但这并不影响推出国债期货交易后长期功能的发挥。可以设想，如果越来越多的机构投资者对国债期货交易完全了解并积极参与，那么国债期货的交易将逐步发挥稳定市场利率的功能。

参考文献

[1]Grinblatt M,Jegadeesh N. Relative pricing of Eurodollar futures and forward contracts[J].The Journal of Finance, 1996, 51(4): 1499-1522.

[2]Cecchetti S G, Cumby R E, Figlewski S. Estimation of the optimal futures hedge[J]. The Review of Economics and Statistics, 1988: 623-630.

[3]Johansen S. Statistical analysis of cointegration vectors[J]. Journal of economic dynamics and control, 1988, 12(2): 231-254.

[4]袁东.论中国利率市场化进程与利率期货的推出[J].财贸经济,2003(6)

[5]党剑.利率市场化与国债期货[J].南开经济研究,2002(1) .

[6]贺强,辛洪涛.重推国债期货与我国利率市场化互动关系研究[J].价格理论与实践，2012(2)

[7]周冰,陈杨龙.国债期货核心功能研究及实证检验——基于我国国债期货仿真交易观察[J].财政研究，2013(4).

Impact of Re-launching the Treasury Bonds Futures on the Volatility Market Interest Rates

Xia Xiuxiang, Hou Qingtian, Zhong Dunhui

(School of Finance, Anhui University of Finance and Economics, Bengbu，Anhui 233000，China)

Abstract：With the data of treasury bond futures (09/06/2013—04/11/2014) and the government bond index (01/04/2013—04/11/2014), we establish some dummy variable for lunching treasury bond futures to set up the GARCH, GJR models to analyze the role of treasury bonds futures. The result shows that negative leverage effect was improved, investors become more rational, market risk was reduced. However, the effect of the futures trading to the market volatility rate is extremely limited. The paper explains the inconsistency of the experimental data with the old theory which holds that the transmission of market information would be slowdown . In this paper, we proved that the treasury bond futures would contribute to development of basic interest rate of financial market, and can provide a hedge against interest rate changes.

Key words：treasury bond futures; treasury spot; GARCH model; GJR model

Class No.:F832.5Document Mark：A

(责任编辑：宋瑞斌)