利用分段积分识别阻尼比研究
2016-01-15赵晓丹,徐俊杰,王西富
第一作者赵晓丹男,博士,教授,1963年7月生
利用分段积分识别阻尼比研究
赵晓丹,徐俊杰,王西富
(江苏大学汽车与交通工程学院,江苏镇江212013)
摘要:提出利用分段积分列方程识别阻尼比方法。用快速傅里叶变换加连续傅里叶变换(Fast Fourier Transform plus Continuous Fourier Transform,FFT-FT)识别响应信号固有频率,并据此构造复指数函数;与响应信号进行两次时间不同的内积运算,控制运算时间为响应信号半周期整数倍;推导衰减系数计算公式,识别阻尼比。该方法具有控制内积运算时间消除负频率项影响特点,不受阻尼大小、采样长度限制,识别精度高,结合迭代运算能识别密集模态阻尼。仿真计算、实验表明,在曲轴阻尼实验中,该方法能准确识别阻尼的微小变化,具有工程实用性。
关键词:分段积分;衰减系数;阻尼比;曲轴
基金项目:江苏大学高级专业人才科研基金资助项目(11JDG096);江苏高校优势学科建设工程基金资助项目(苏政办发[2011]6号)
收稿日期:2014-05-26修改稿收到日期:2014-09-30
中图分类号:TB123
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.20.019
Abstract:A method using piecewise integral to identify damping ratios was proposed. The natural frequency was calculated based on a response signal by the application of Fast Fourier Transform plus Continuous Fourier Transform (FFT-FT). A complex exponential function was constructed with the calculated natural frequency, two inner products with different integral time were conducted between the response signal and the constructed exponential function, the operation time of inner products was controlled to be integer times of semi-period of the response signal, and then the formula of attenuation coefficient was derived. As a result, the damping ratio was determined. The feature of the method is that the interference by negative frequency item is eliminated by controlling the operation time of inner products. The method is not restricted by the size of damping ratios and the length of sample, and it has high precision. Damping ratios of closely spaced modes can be also identified by the method combined with iterative algorithm. Digital simulations and experiments show that the method is effective. In crankshaft experiments, small changes of damping ratios were identified. The method is practical in engineering.
Method for damping identification using piecewise integral
ZHAOXiao-dan,XUJun-jie,WANGXi-fu(School of Automobile and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China)
Key words:piecewise integral; attenuation coefficient; damping ratio; crankshaft
阻尼在结构故障诊断、振动实时监控、荷载识别、噪声控制及动力响应等研究中有重要意义[1-2];但阻尼的识别精度一直不高,受测量方法影响较大,提高阻尼比识别精度成为主要研究目标[3]。测量阻尼主要有时、频域识别方法,时域识别方法包括自由衰减法、ITD法、STD法、ARMA方法衍生及随机减量技术等;频域识别方法最经典的为半功率带宽法;另外有小波变换[4-5]、EMD-HT[6]等方法。小波变换存在端点效应等[7-8];而EMD-HT方法需用模态经验分解(EMD),但EMD包络线计算存在过冲、欠冲,数据端点处理困难,存在提取模态不完整及出现虚假模态问题[9]。实际工程应用中最多的为半功率带宽法[10]。该法因受频率分辨率影响,识别精度受系统阻尼值大小限制。半功率带宽改进方法虽通过频谱细化后阻尼比估计精度有较大提高,但由于小阻尼下时域截断造成能量泄漏产生截断误差,受采样长度影响较大。为此,本文提出利用分段积分列方程求解阻尼方法,精度高,不受阻尼大小及采样长度限制。仿真计算及曲轴实验结果均表明本文方法的有效性。
1利用分段积分计算阻尼比
推导利用分段积分计算阻尼比公式,忽略负频率项的积分结果,简化过程;在此基础上通过控制积分时间消除负频率项影响,提高阻尼识别精度。并推广到多自由度系统进行阻尼识别。
1.1忽略负频率项影响的分段积分法
线性单自由度有阻尼系统的振动微分方程为
(1)
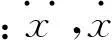
该系统自由衰减振动响应可表示为
x(t)=Ae-ntcos(ωdt+φ)=
(2)
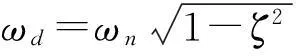
对响应信号x(t)用连续傅里叶变换计算FFT谱局部区间频率细化计算方法(FFT-FT)[11-12]识别出共振频率ω≈ωd。由ω构造指数函数e-jωt并与响应信号x(t)乘积作积分运算,积分区间[0,T1],令积分结果为C1,得
(3)
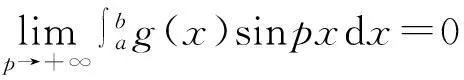
(4)
同理,将响应信号x(t)与指数函数e-jωt的乘积作第二段积分运算,积分区间[0,T2],令T2=2T1,用C2表示该时间段积分,有
(5)
C1,C2的计算结果为同相位复数,由于式(4)、(5)忽略负频率项影响,实际计算中存在细微相位偏差,故C1,C2分别取绝对值。令e-nT1=x,由式(4)、(5)可得关系式为
(6)
由于e-nT1=x,由式(6)解得
(7)
式中:ln(·)表示取自然对数。
据识别的固有频率ω(ω≈ωd)及衰减系数n可得阻尼比为
(8)
在识别出阻尼比基础上可利用本文方法识别响应信号幅值及初相位以识别模态信号。据识别的ω及n构造函数f(t)=e-ntejωt+e-nte-jωt,将其与e-jωt的乘积作积分运算,积分区间[0,T1],积分结果C3可表示为
(9)
对比式(9),与式(3)同理,C3可表示为
(10)
由式(4)、(10)得
(11)
式(11)计算结果为复数,由此可识别振幅A及初始相位φ,即
(12)

1.2消除负频率项影响
以上推导忽略负频率项的积分结果理论上存在不完善性,但为进一步研究奠定基础,故研究如何消除负频率项影响完善分析。令式(3)中负频率项积分结果为D1,得
(13)
利用分部积分法计算D1,即
(14)
由式(14)得D1的积分结果为
(15)
将式(15)代入式(13),得C1完整表达式
(16)
第二段积分同理,T2=2T1得C2完整表达式
(17)
分析式(16)、(17)发现,当T1=mπ/ω(m为正整数)即T1为响应信号半周期的整数倍时,cos(2ωT1)=cos(4ωT1)=1,sin(2ωT1)=sin(4ωT1)=0。进一步化简得
(18)
(19)
式(18)、(19)为由控制积分运算时间获得C1、C2完整表达式,推导中未限制阻尼值大小及时间长短,通过控制积分运算时间为响应信号半周期整数倍可消除原负频率项积分对计算影响,使识别精度更高。通过二式仍可获得式(6)~式(8),求出阻尼比。
1.3多自由度系统阻尼识别
解决单自由度系统的阻尼识别远远不够,实际工程中多为多自由度情况,故讨论利用分段积分法对多自由度下的阻尼进行识别。
多自由度系统分为非密集模态、密集模态。非密集模态间干扰作用较弱,可视为多个独立的单自由度信号,用分段积分法直接识别。而密集模态间干扰作用强,视为由N阶模态相互干涉构成,即
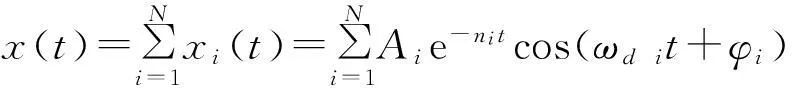
(20)
2仿真计算
2.1单自由度系统仿真算例

表1 三种方法阻尼比计算结果比较
考察采样时间长度对本文方法影响。模拟信号取表1阻尼比0.004的响应信号,改变积分时间长度,用考虑、不考虑负频率项影响分段积分法进行阻尼识别。不考虑负频率项影响分段积分法积分时间自由选取,即T1分别取0.2 s、0.4 s、0.5 s;考虑负频率项影响的分段积分法积分时间需控制选取响应信号半周期的整数倍,T1分别取0.066 48 s、0.265 87 s、0.465 27 s(即为10、40、70个响应信号周期),识别结果见表2。由表2看出,不考虑负频率项影响的分段积分法采用不同积分时间,相对误差有一定波动,计算结果受积分时间影响;考虑负频率项影响的分段积分法用不同积分时间,计算结果稳定,相对误差变化较小约0.09%,说明其不受采样长度限制。
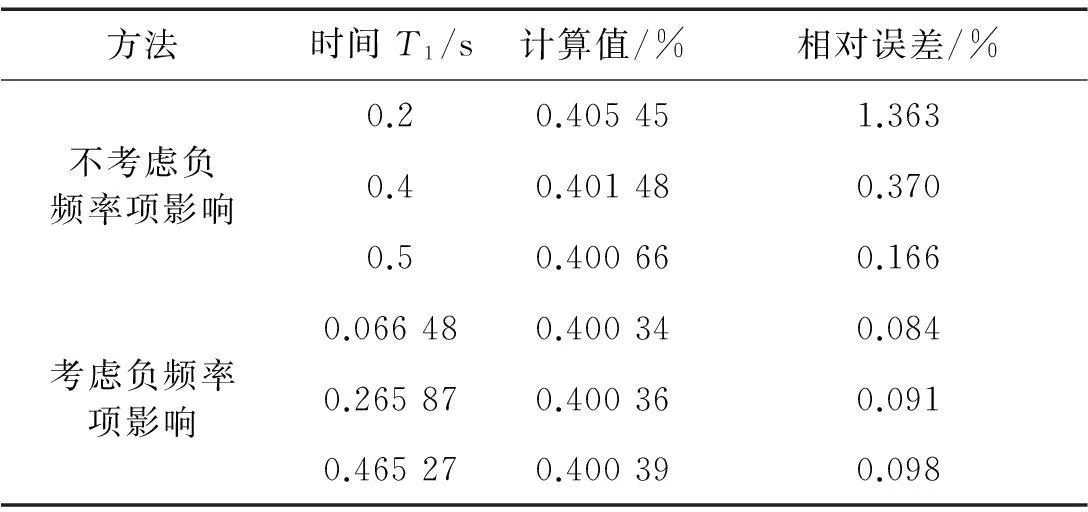
表2 积分时间对阻尼比计算结果的影响
2.2多自由度系统仿真算例
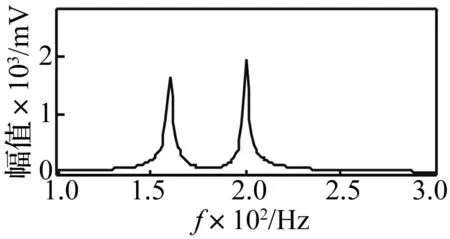
图1 非密集模态频域图 Fig.1 Frequency spectrum ofnon-closely spaced modes
二自由度有阻尼系统自由衰减响应见式(20),其中i=2,A1=13,φ1=π,A2=12,φ2=π/6,ζ1=0.008,ζ2=0.005。非密集模态令信号频率f1= 160 Hz,f2=200 Hz;密集模态令f1=196 Hz,f2=200 Hz。采样频率2 000 Hz,取分析点数2 000用于诊断信号频率,积分时间T1取40个信号周期。非密集、密集模态频域图见图1、图2,识别结果见表3、表4。由表3看出,由于非密集模态间相互影响不大,内积运算具有一定滤波作用,用分段积分法可直接识别非密集模态阻尼,识别精度较高。由表4看出,密集模态间干扰作用强,用分段积分法直接进行识别误差较大;分段积分法结合迭代运算能有效消除模态间干扰;而经5次迭代的计算结果识别精度较高,控制在1%以下。因此结合迭代分段积分法也能对密集模态阻尼进行识别。
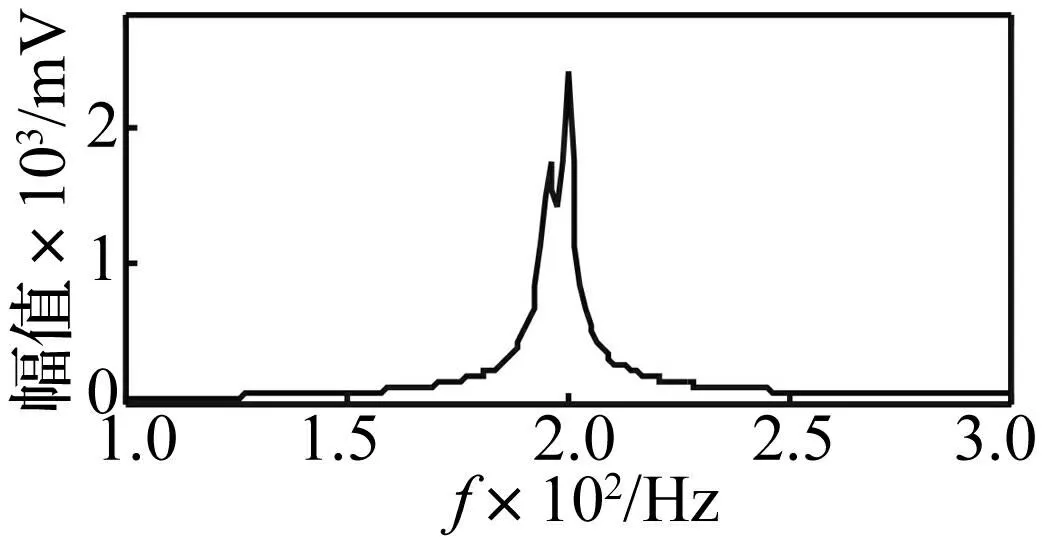
图2 密集模态频域图 Fig.2 Frequency spectrum of closely spaced modes
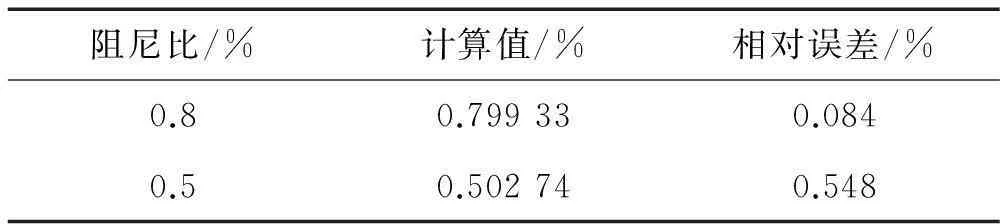
阻尼比/%计算值/%相对误差/%0.80.799330.0840.50.502740.548
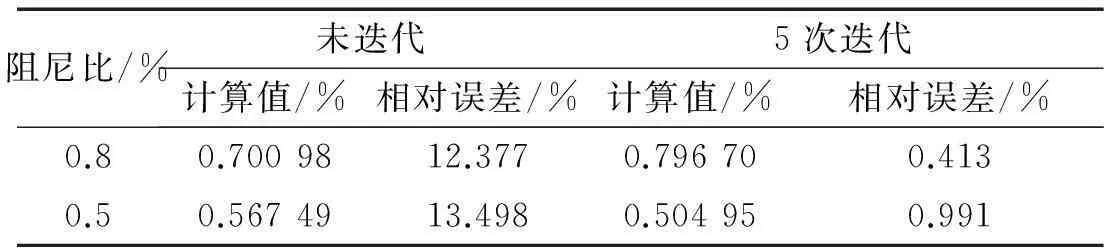
表4 密集模态阻尼识别结果
3模拟曲轴阻尼微小变化实验
阻尼对裂纹的敏感性较强[14],能准确诊断不同时期阻尼,有助于识别曲轴裂纹。将本文方法用于曲轴阻尼诊断,改变曲轴阻尼模拟裂纹出现。实验选某型号六缸发动机曲轴,两端通过橡皮绳水平悬空吊起,用型号B&K 8848的铜质力锤敲击曲轴第三缸连杆曲颈处,用曲轴臂上型号B&K 4321的加速度传感器记录曲轴振动信号。曲轴产生裂纹损伤时引起刚度、阻尼变化。实验在曲轴连接第三缸连杆轴颈及主轴颈曲轴臂上粘贴质量轻的阻尼片,引起阻尼变化,模拟曲轴在该处出现裂纹,此处应力集中[15]易产生裂纹。依次增加阻尼片数量,共进行4组实验,实验照片见图3。

图3 曲轴实验照片 Fig.3 The photo of crankshaft experiment
设采样频率10 000 Hz,分析点数20 000,采集信号的时、频域图见4、图5。由图5看出,信号在频率2 500 Hz附近有个最明显谱峰,约700 Hz。可将此频率对应的模态设为特征模态。


图4 曲轴响应信号时域图Fig.4Timedomainspectrumofcrankshaftsresponsesignal图5 曲轴响应信号频域图Fig.5Frequencyspectrumofcrankshaftsresponsesignal图6 剩余信号频域图Fig.6Frequencyspectrumoftheremainingsignal
用本文方法对特征模态进行阻尼识别,且诊断出幅值、相位角,提取特征模态信号,积分时间T1取300个信号周期;从总信号中减去识别的模态信号获得剩余信号频域图,见图6。由图6看出,在2 500 Hz左右特征频率处模态几乎被完全消减,消减后幅值低于10,远小于图5中原信号在特征频率处幅值,表明本文方法识别结果准确。
用消除负频率项影响的分段积分法对曲轴产生裂纹即粘贴阻尼片时特征模态进行阻尼识别。诊断结果见表5。由表5看出,考虑负频率项影响的分段积分法三次识别值变化符合粘贴轻质阻尼片使曲轴阻尼增大规律,说明本文方法可识别出阻尼的微小变化,有助于识别裂纹。
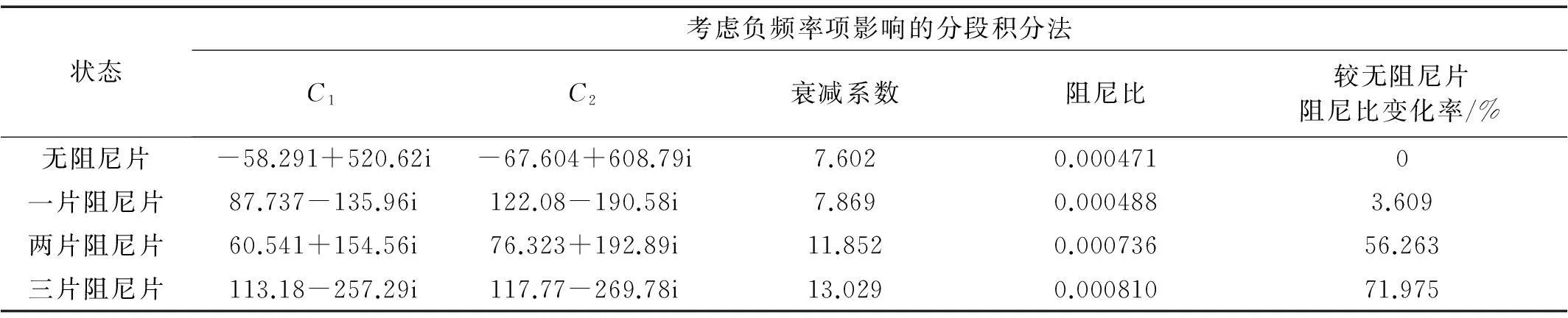
表5 曲轴阻尼比识别结果
4结论
(1)本文提出的利用分段积分列方程识别阻尼比方法通过两次时间不同内积运算识别阻尼比,控制内积运算的时间可消除负频率项影响,且不受系统阻尼值大小限制,可准确识别高、中、低3种不同阻尼值。
(2)利用分段积分列方程识别阻尼方法不受采样长度影响,计算结果稳定。识别过程中进行两段积分时间不同的内积运算,无需像半功率带宽法搜索半功率带宽点,计算过程简便,且识别精度高。
(3)结合迭代分段积分法亦能识别密集模态阻尼。在识别曲轴阻尼实验中,准确识别出阻尼的微小变化,有助于识别曲轴裂纹,具有工程实用性。
参考文献
[1]于开平,邹经湘,庞世伟. 结构系统模态参数识别方法研究进展[J]. 世界科技研究与发展,2005,27(6):22-30.
YU Kai-ping,ZOU Jing-xiang,PANG Shi-wei. Research advance of modal parameter identification medthod for structural system[J]. Journal of World Sci-tech R. & D.,2005,27(6):22-30.
[2]张淼,于澜,鞠伟. 基于频响函数矩阵计算尼系统动力响应的新方法[J]. 振动与冲击,2014,33(4):161-166.
ZHANG Miao, YU Lan, JU Wei. A new method for computing dynamic response of a damped linear system based on frequency response function matrix[J]. Journal of Vibration and Shock,2014,33(4):161-166.
[3]王慧,刘正士. 一种识别结构模态阻尼比的方法[J]. 农业机械学报,2008,39(6):201-202.
WANG Hui,LIU Zheng-shi. A method identification of structural damping ratios[J]. Journal of Transactions of the Chinese Society for Agricultural Machinery,2008, 39(6):201-202.
[4]Lamarque C H,Penrot S,Cuer A. Damping identification in multi-degree-of-freedom systems via a wavelet-logarithmic decrement-part 1: theory[J]. Journal of Sound an Vibration,2000,235 (3):361-375.
[5]Staszewski W J. Identification of damping in MDOF systems using time-scale decomposition[J]. Journal of Sound and Vibration,1997,203 (2):283-305.
[6]Chen J,Xu Y L, Zhang R C. Modal parameter identification of tsing ma suspension bridge under typhoon victor: EMD-HT method[J]. Journal of Wind Engineering and Industrial Aerodynamics,2004,92: 805- 827.
[7]伊廷华,李宏男,王国新. 基于小波变换的 结构模态参数识别[J]. 振动工程学报,2006,19(1):51-56.
YI Ting-hua,LI Hong-nan,WANG Guo-xin. Structural modal parameter identification ba-sed on wavelettransform[J].Journal of Vibration Engineering,2006,19(1):51-56.
[8]Tan Jiu-bin,Liu Yan,Wang Lei. Identification of modal parameters of a system with high damping and closely spaced modes by combining continuous wavelet transform with pattern search [J]. Mechanical Systems and Signal Processing,2008, 22:1055-1060.
[9]王慧,刘正士,陈恩伟. 悬臂梁结构模态参数Hibert-Huang变换识别方法[J]. 农业机械学报,2008,39(9): 187-191.
WANG Hui,LIU Zheng-shi,CHEN En-wei. Application of HHT for modal parameters I-dentification to cantilever beam structure[ J]. Transactions of the Chinese Society for Agricultural Machinery,2008,39(9):187-191.
[10]陈奎孚,张森文. 半功率法估计阻尼的一种改进[J]. 振动工程学报,2002,15(2):151-155.
CHEN Kui-fu,ZHANG Sen-wen. Improvement on the damping estimation by half powerpoint method[J]. Journal of Vibration Engineering,2002,15(2):151-155.
[11]刘进明,应怀樵. FFT谱连续细化分析的傅里叶变换法[J]. 振动工程学报,1995,8(2):162-166.
LIU Jin-ming,YING Huai-qiao. Zoom FFT spectrum by Fourier transform[J]. Journal of Vibration Engineering,1995,8(2):162-166.
[12]赵晓丹,张忠业,骆英.基于内积运算与迭代算法的密集模态阻尼识别[J].农业机械学报,2011,42(4):206-210.
ZHAO Xiao-dan,ZHANG Zhong-ye,LUO Ying. Damping identification for closely s- paced modes based on inner product calcu lation and iterative algorithm[J].Journal of Transactions of the ChineseSociety for Agricultural Machinery,2011,42(4):206-210.
[13]赵红发,南广仁. Riemann-Lebesgue定理的推广[J]. 长春师范学院学报:自然科学版,2008,7(5):3-4.
ZHAO Hong-fa,NAN Guang-ren. The prom otion of Riemann-Lebesgue theory[J].Journal of Changchun Normal University,2008,7 (5):3-4.
[14]张敬芬,赵德友. 工程结构裂纹损伤振动诊断的发展现状和展望[J]. 振动与冲击,2002,21(4):22-26.
ZHANG Jing-fang,ZHAO De-you. Summary review of vibration-based crack diagnosis technique for engineering structures[J]. Journal of Vibration and Shock,2002,21(4):22-26.
[15]李学鹏. 汽车发动机曲轴断裂原因分析[J]. 内燃机与动力装置,2011,2:50-52.
LI Xue-peng. Failure analysis of crankshaft in automobile engine[J]. Journal of I.C.E & Power Plant,2011,2:50-52.