采用附加耗能构件的双柱式高墩地震损伤控制研究

第一作者谢文男，博士，讲师，1981年生

邮箱：xiewen@nbu.edu.cn

采用附加耗能构件的双柱式高墩地震损伤控制研究

谢文1，孙利民2

(1.宁波大学建筑工程与环境学院，浙江宁波315211； 2.同济大学土木工程防灾国家重点实验室，上海200092)

摘要：提出在墩柱间附加耗能构件的地震损伤控制策略，耗散地震输入确保墩柱处于弹性或只发生轻微损伤，且震后易于修复或更换。利用弹塑性动力方法并引入位移、Park损伤指数及曲率延性系数作为评价指标，研究附加耗能构件对极端地震(PGA=1.0 g)作用下双柱式高墩的地震损伤控制效果，探讨、验证该控制策略的有效性及可行性。结果表明，损伤控制(附加耗能构件)的双柱式高墩墩顶位移及墩底曲率、Park损伤指数及曲率延性系数明显低于控制前，且墩底截面弯矩变化较小；附加耗能构件对双柱式高墩的损伤控制效果明显，满足损伤控制目标。

关键词：双柱式高墩；剪切连梁；约束屈曲支撑；损伤控制策略；地震损伤指标

基金项目：国家自然科学基金项目(91315301)；浙江省自然科学基金项目(LY15E080011)；浙江省教育厅科研项目(Y201430900)；宁波市自然科学基金项目(2015A610294)

收稿日期：2014-12-03修改稿收到日期：2015-04-09

中图分类号:U442.55; TU311.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.20.017

Abstract:A seismic damage control strategy, that is, adding energy dissipation elements, easily reparable or replaceable, between two columns, was presented. The control strategy was designed to dissipate seismic energy by the energy dissipation elements, while keeping the columns elastic or minor damaged. In order to study the effectiveness of the energy dissipation elements on seismic damage control of twin-column tall piers, elasto-plastic time history analyses were performed on models of the twin-column tall pier with the height of 60 m under extreme earthquake (PGA=1.0g) according to seismic damage indices, such as displacement, Park damage indices and curvature ductility factor. Compared with the twin-column tall piers without energy dissipation elements, the indices of the twin-column tall piers with energy dissipation elements after being damaged are significantly reduced, including the maximum displacement at the column top, the maximum curvature at the column bottom, the Park damage indices and the curvature ductility factor at the column. And the maximum moment of the column bottom of the twin-column pier with energy dissipation elements before and after being damaged can maintain almost unchanged. It is shown that the proposed strategy is effective and feasible to seismic damage control of the twin-column tall piers and the columns can keep safe even under extreme earthquake.

Seismic damage control for twin-column tall piers by using supplemental energy dissipation elements

XIEWen1,SUNLi-min2(1. Faculty of Architectural, Civil Engineering And Environment, Ningbo University, Ningbo 315211, China；2. State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)

Key words:twin-column tall pier; shear link; buckling restrained brace; damage control strategy; seismic damage index

双柱式高墩桥梁在我国铁路、公路建设中应用较广，尤其地震频发的西部地区。因高墩具有截面尺寸大、结构周期长、墩身质量大等特点，我国公路桥梁抗震设计规范对其抗震性能仅有原则性指导意见。而具有高延性能力桥梁(如桥墩)遭受强震后尽管不会发生倒塌，但会发生较大残余位移[1]，需高昂费用修复甚至重建。为克服延性桥墩震后发生较大残余变形的不足，Mander等[2]提出干接缝无粘结预应力节段拼装桥墩，但主要集中于独柱式桥墩及低矮双柱式桥墩。El-Bahey等[3-5]将结构保险丝概念引入双柱式桥墩抗震设计、修复中，即在墩柱间增设易于修复或更换的保险丝构件耗散地震输入能以确保墩柱处于弹性或轻微损伤，并通过拟静力试验及数值方法分析不同保险丝构件对双柱式矮墩抗震性能影响。孙利民等[6-7]通过拟静力试验研究附有保险丝构件的双柱式高墩抗震性能，但试验模型并非真正意义的高墩，因其无法体现高墩的动力特点及高阶效应，且未考虑地震动影响。在大跨度桥梁抗震领域，Cole等[8]研究剪切连杆及安装部位对旧金山-奥克兰海湾桥主塔抗震性能影响。在建筑结构抗震领域，为改善剪力墙之间连梁的抗震性能，Fortney等[9]提出可更换、带保险丝的钢连梁。Vargas等[10]据提出的简化方法设计附加不同保险丝构件的常规框架结构，并试验验证。之后该理念获得进一步发展[11-16]。可见，结构保险丝概念已广受关注，而大多研究集中于建筑结构，在桥梁结构尤其双柱式高墩中鲜有研究、应用。尽管保险丝概念在主塔等超高结构中有所研究与应用，但双柱式高墩与其受力特点及抗震能力明显不同，构件的耗能机理亦不同。

本文采用弹塑性动力分析方法并引入Park损伤指数、曲率延性系数及位移等指标评价双柱式高墩地震损伤控制效果；提出在高墩柱间附加震后易于修复或更换的耗能构件(以约束屈曲支撑及剪切连梁为例)，通过其耗散地震输入能确保墩柱处于弹性或轻微损伤状态，使地震后墩柱无需修复或稍加修复即可恢复使用功能。以墩高60 m的双柱式桥墩为例，在极端地震荷载(PGA=1.0 g)作用下，用数值方法探讨、验证损伤控制策略的有效性与可行性。

1双柱式高墩地震损伤分析方法

在地震往复荷载作用下双柱式高墩会遭受不同程度损伤，如裂缝、塑性变形等。地震损伤指标不仅用于量化构件、结构的损伤程度，也为抗震设计及损伤控制基础。

1.1能量分析模型

地震作用下双柱式高墩运动方程为

(1)

EK+ED+EH+ES=EI

(2)

式中：EK，ED，EH，ES分别为双柱式高墩瞬时动能、累积阻尼耗能、累积滞回耗能及瞬时弹性应变能； 为地震输入总能量，即

(3)

对给定地震输入，可据式(1)进行弹塑性时程分析，求得双柱式高墩位移响应向量X及单元构件弯矩与曲率，即可计算结构单元的累积滞回耗能EH，进一步获得其地震损伤程度与分布。

1.2地震损伤指标

在地震往复荷载作用下，结构损伤、破坏由其强度、变形能力及累积耗能性能等因素共同决定。为合理反应弹塑性变形与地震引起的低周疲劳效应，Park等[17]提出可考虑位移与耗能等因素共同影响的损伤指标(Damage indices, DI)，即由构件最大变形及累积滞回耗能线性叠加而成，表达式为

(4)

式中：xm，xu分别为构件地震响应最大位移及构件极限位移能力；Fy为构件屈服强度；EH为构件在地震作用过程中的累积滞回耗能；β为耗能因子或强度退化参数，计算式为

β=(-0.447+0.073λ+0.24n0+0.314ρt)0.7100ρω

(5)

式中：λ为构件剪跨比；n0为轴压比；ρt为纵向受力钢筋配筋率(含百分号)；ρω为体积箍筋率(不含百分号)。

为计算简便，Kunnath[18]对Park损伤模型略作修改，从截面层次计算结构损伤，即去除弹性变形对第一项影响，用屈服弯矩、曲率替代屈服力及位移，即式(4)修正为

(6)

式中：φm，φu分别为截面地震响应最大曲率及极限曲率；φy,My分别为截面屈服曲率、屈服弯矩。

对以压弯受力为主的构件，累积滞回耗能EH可通过单元塑性铰区弯矩-曲率的滞回曲线积分获得。

1.3地震破坏准则

损伤指标可描述地震引起的桥梁结构损伤。对在强震作用下易进入塑性变形的钢筋混凝土构件，用Park损伤指标可合理描述以受压弯为主构件的地震损伤程度。其损伤等级分为无损伤、轻微损伤(DS2)、中等损伤(DS3)、严重损伤(DS4)及局部失效或倒塌(DS5)，对应的损伤指数分别为0～0.1、0.1～ 0.25、0.25～0.4、0.4～1.0及大于1.0，超过1.0表示结构已倒塌或局部失效[17]。为此，本文用截面曲率延性系数作为地震损伤指标，即将各损伤状态对应的截面临界曲率除以截面屈服曲率，获得截面曲率延性系数。地震损伤状态与破坏准则见表 1。其中，εy，εsu分别为钢筋屈服应变、极限应变；εcu为核心混凝土极限应变；εs，εC分别为钢筋及约束混凝土应变响应；φy，μ分别为截面屈服曲率及曲率延性系数。

表1　基于截面曲率延性系数的地震破坏准则

2双柱式高墩地震损伤控制策略

2.1地震损伤控制策略

由式(4)或(6)的损伤指标看出，双柱式高墩的地震损伤主要由变形与累积耗能所致。由式(1)、(2)可知，地震总输入能EI最终只转化为双柱式高墩的阻尼耗能ED与滞回耗能EH，因双柱式高墩动能EK与弹性应变能ES终将趋向于0，故可通过措施控制双柱式高墩的地震损伤，即①提高其自身的阻尼耗能能力；②提高其自身的滞回耗能能力；③附加非结构耗能构件，合理调整墩柱与构件间刚度及耗能力比。

地震作用下，地震总输入能EI由双柱式高墩的阻尼及滞回耗能消耗。其中双柱式高墩自身阻尼为固有特性，较难改变或提高；而可行的措施则为②、③。提高墩柱自身滞回耗能能力措施主要有：外包钢管或碳纤维布、内置型钢或碳纤维筋、塑性铰区箍筋加密或设置橡胶层等，但用传统措施的桥墩在遭受强震尤其极端地震后其塑性变形集中于塑性铰区，会发生较大残余位移，影响墩柱震后修复或重建。因此本文提出损伤控制策略为：在墩柱间附加震后易于修复或更换的非结构耗能构件，通过其耗散地震输入能确保墩柱处于弹性或轻微损伤状态，使墩柱无需修复或稍加修复即可恢复正常功能。

2.2地震损伤控制目标

以地震损伤指标作为损伤控制效果的评价指标，在极端地震(PGA=1.0 g)作用下，双柱式高墩损伤应控制在弹性状态或轻微损伤内，Park损伤指数小于0.10或0.25，截面曲率延性系数应控制在1或5内。需指出的是，该截面曲率延性系数等于截面最大曲率响应与受拉钢筋首次屈服时的曲率之比；同时须保证高墩损伤后不能过多丧失竖向承载能力，其屈服强度应尽量低以使桥墩基础水平剪切承载能力较小，降低基础的建设费用。

3双柱式高墩地震损伤控制算例

3.1双柱式高墩概况

双柱式高墩为某大跨度斜拉桥中的辅助墩，墩高60 m，墩柱截面尺寸5.2 m×8.5 m，壁厚1.5 m，墩柱中心间距10.4 m。为减小墩柱顶端弯矩及底部剪力、增大耗能构件耗能力，墩柱与盖梁间采用铰接，墩柱底部与基础固结，简称“a式高墩”，见图 1(a)、(d)。墩柱截面纵向钢筋配筋率1.7%，箍筋体积配箍率1.2%，满足公路桥梁抗震设计规范要求。

图1　双柱式高墩的立面与截面型式(单位：m) Fig.1 Elevation view and cross-section of twin-column tall piers (unit: m)

以约束屈曲支撑(Buckling Restrained Braces, BRBs)及剪切连梁(Shear Links, SLs)为例，阐明附加耗能构件对双柱式高墩地震损伤控制效果。据裸双柱式高墩抗震性能参数，用损伤控制方法设计[19]BRBs及SLs截面，并用Q235加工制作。其中须确保BRBs及SLs先于墩柱屈服，见图 2。分别将12根BRBs、10根SLs附加于墩柱间，分别简称为“b式高墩”、“c式高墩”(图 1(b)及(e)、(c)及(f))。安装后的BRBs构件与水平方向约45°，SLs沿墩高间隔10 m安装。

图2　BRBs及SLs截面尺寸(单位：m) Fig.2 Cross-section of BRBs and SLs (unit: m)

3.2有限元模型

用OpenSees分别建立考虑几何、材料非线性的各式高墩有限元模型，见图 3。墩身用纤维梁单元模拟，忽略单元剪切变形并假设扭转处于弹性状态；墩顶连杆用弹性梁单元模拟，释放梁端转动自由度；上部结构影响用高墩分担的重量近似，即用集中质量作用于高墩顶部；忽略基础与地基间相互作用，高墩固定于地基上。钢筋、混凝土材料的本构模型分别用修正的Menegotto & Pintom及Mander。弹塑性地震响应分析中阻尼取5%，用Rayleigh阻尼矩阵计算Rayleigh系数时取基频与对动力反应有显著贡献的振型频率。

图3　双柱式高墩计算模型 Fig.3 Finite element model of twin-column tall piers

BRBs属于轴向拉压型屈服耗能构件，用桁架单元模拟，建模时将同高度的两根BRBs面积等效成一根桁架单元面积；单元两端铰接，不传递弯矩；由于BRBs两端与墩柱中心有一定间距，故用刚臂单元模拟；本构模型采用双线性模型，用OpenSees材料库中的Steel01模拟。

SLs属于剪切型屈服耗能构件，用考虑剪切变形的纤维梁单元模拟，即纤维梁单元截面信息除考虑弯矩-曲率关系外亦考虑剪力-剪切变形关系，后者由剪力-剪切角关系曲线描述，在OpenSees中通过截面信息组合集成实现。对设计的低屈服工字钢SLs，屈服剪力Vy计算式为

(7)

式中：σyω为腹板屈服正应力；tω为剪切连梁腹板厚度；d为剪切连梁高度；tf为剪切连梁翼缘厚度。

线弹性阶段剪切角计算式为

(8)

式中：k为因切应力沿截面分布不均匀引起与截面形状有关的系数，工字形截面k=A/Aω为全截面面积，Aω为腹板面积；G为剪切模量。

需指出的是，建模或计算时将同一高度两个SLs等效成一个剪切连梁单元。SLs的本构模型假设为双线性模型，用OpenSees材料库中的Steel01模拟。

3.3地震输入

设双柱式高墩属A类桥梁结构，抗震设防烈度为9度。据规范[20]，该高墩在E1地震作用下的设计地震动加速度峰值A=0.4 g。为考虑极端地震作用下双柱式高墩的损伤控制分析，将A提高至1.0 g作为极端地震输入，采用已建某特大跨度桥梁的场地条件及3条设计地震动，加速度时程见图4。

图4　设计地震动加速度时程 Fig.4 Acceleration time history of design ground motions

选用这些地震波主要由于：①该双柱式高墩据图 4地震动进行抗震设计，即高墩遭受该期望的地震荷载不会发生倒塌；②实际地震记录一般含有脉动波成分，而反应谱方法不能精确衡量桥梁结构的弹塑性地震响应，即当桥梁结构考虑非线性影响时，即使采用相同反应谱的地震波也不能保证地震响应相同，因此需考虑多条地震输入；③该设计地震动的卓越周期和频率成分可反映我国沿海地区工程地质场地特征。

3.4结果分析

用Newmark-β法对双柱式高墩进行弹塑性地震响应分析。β=0.25，时间积分间隔为0.02 s。据位移响应、Park损伤指数、曲率延性系数及弯矩-曲率关系等损伤指标评价采用附加耗能构件损伤控制方法的有效性，位移响应及弯矩-曲率关系为单条地震响应结果，而Park损伤指数及曲率延性系数为3条地震响应结果平均值。

3.4.1附加耗能构件对双柱式高墩位移响应影响

第1条极端地震波作用下各式高墩(a式、b式和c式高墩)墩顶位移响应见图5。由图5分析知，与a式高墩(裸双柱式高墩)相比，附加耗能构件(BRBs及SLs)后b式、c式高墩最大水平位移显著减小，约为a式高墩的1/2。主要因附加耗能构件后高墩刚度明显增大；附加的耗能构件对高墩残余变形影响不明显，各式高墩残余变形均可忽略。

图5　第1条地震波作用下各式高墩墩顶位移响应 Fig.5 Displacement response at top of all tall piers under the 1st ground motion

第2、3条极端地震波作用下a、b、c式高墩墩顶位移响应见图6、图7。与图 5结果有相似之处，即附加耗能构件后双柱式高墩最大水平位移明显小于裸双柱式高墩，而对残余变形影响不明显，各式高墩残余变形均较小。

图6　第2条地震波作用下各式高墩墩顶位移响应 Fig.6 Displacement response at top of all tall piers under the 2nd ground motion

图7　第3条地震波作用下各式高墩墩顶位移响应 Fig.7 Displacement response at top of all tall piers under the 3rd ground motion

3.4.2附加耗能构件对双柱式高墩地震损伤影响

极端地震波作用下a、b、c式高墩的Park损伤指数分布见图8。由图分析知，与a式高墩相比，b、c式高墩的Park损伤指数明显降低。以损伤最严重的墩底截面为例，a、b、c式高墩的Park损伤指数分别为0.497、0.217、0.049，其损伤状态为严重损伤、轻微损伤及弹性状态，附加耗能构件对双柱式高墩的地震损伤控制效果非常明显，且使墩柱满足损伤控制目标。主要原因为附加的耗能构件先于墩柱屈服，起到作用，减轻墩柱的地震损伤。而c式桥墩地震损伤明显低于b式，尽管BRBs的耗能能力强于SLs，但BRBs增大双柱式高墩的刚度比SLs更明显，致b式高墩中墩柱截面弯矩及曲率需求变大，见图9。

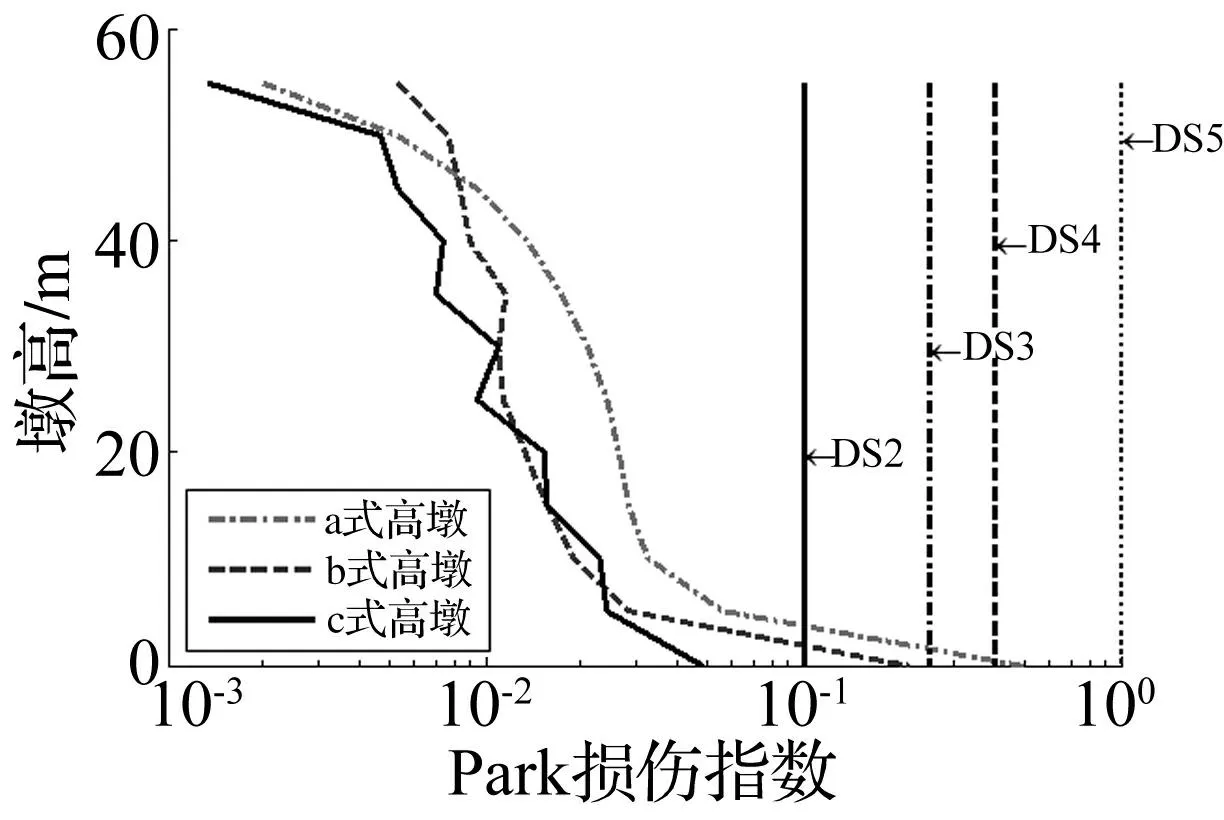
图8　3条地震波作用下各式高墩Park损伤指数均值 Fig.8 Average Park damage indices of all tall piers underall ground motions

图9　耗能构件累积耗能 Fig.9 Cumulative hysteretic energy of dissipation energy elements

极端地震波作用下a、b、c式高墩截面曲率及曲率延性系数见图10、图11。分析两图知，与a式高墩相比，b、c式高墩的截面曲率及其延性系数明显减小。以损伤最严重的墩底截面为例，a、b、c式高墩曲率为5.31E-3、3.642 E-3、9.5 E-4，其曲率延性系数为8.85、6.07、1.584，其损伤状态为中等、轻微及轻微。即使以偏保守截面曲率或其延性系数作为评价指标，附加耗能构件措施对双柱式高墩的地震损伤控制效果也较明显，均满足损伤控制目标。

第2条地震波作用下各式高墩墩底截面弯矩-曲率滞回曲线比较结果见图12。由图12可知，由于附加构件的耗能及刚度效果，b、c式高墩墩底截面曲率响应明显低于a式，曲率减小程度分别高达60%、85%，表明附加耗能构件能控制截面损伤程度；而对截面曲率相应弯矩，b、c式高墩墩底截面最大弯矩仅大于a式2%，明显小于曲率的减小程度。

图10　3条地震波作用下各式高墩截面曲率均值 Fig.10 Average curvature of all tall piers under all ground motions

图11　3条地震波作用下各式 高墩截面曲率延性系数均值 Fig.11 Average curvature ductility coefficient of all tall piers under all ground motions

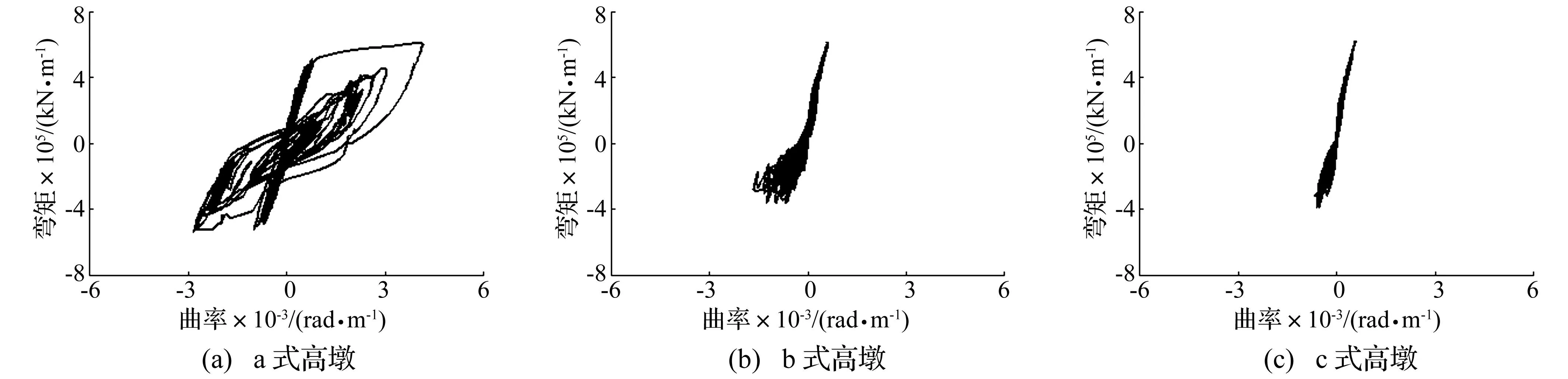
图12　第2条地震波作用下各式高墩墩底截面弯矩-曲率关系 Fig.12 Hysteretic curve of moment-curvature at bottom section of all tall piers under the 2nd ground motion

4结论

(1)提出在墩柱间附加耗能构件的地震损伤控制策略，并以BRBs、SLs作为耗能构件附加在双柱式高墩中进行数值模拟分析，验证该策略的有效性及可行性。

(2)损伤控制后(附BRBs及SLs)的双柱式高墩墩顶位移及墩底曲率、Park损伤指数及曲率延性系数明显低于控制前，且墩底截面弯矩变化较小，表明附加耗能构件的损伤控制效果明显。

(3)在既定损伤控制目标基础上，实现极端地震作用下双柱式高墩损伤控制，且满足控制目标。

参考文献

[1]Kawashima K, MacRae G A, Hoshikuma J I, et al. Residual displacement response spectrum[J]. Journal of Structural Engineering,1998,124(5): 523-530.

[2]Mander J B, Cheng C T. Seismic design of bridge columns based on control and repairability of damage[C]. National Center for Earthquake Engineering Research(NCEER): Buffalo, NY.,1997.

[3]El-Bahey S. Analytical development and experimental validation of a structural-fuse bridge pier concept[C]. State University of New York at Buffalo, Structural and Environmental Engineering: New York, 2010.

[4]El-Bahey S, Bruneau M. Bridge piers with structural fuses and bi-steel columns. I: experimental testing[J]. Journal of Bridge Engineering, 2012,17(1): 25-35.

[5]El-Bahey S,Bruneau M. Bridge piers with structural fuses and bi-steel columns. II: analytical investigation[J]. Journal of Bridge Engineering, 2012,17(1): 36-46.

[6]Sun L, Wei J, Xie W. Experimental studies on seismic performance of subsidiary piers for long span cable-stayed bridge with energy dissipation[J]. Advances in Structural Engineering, 2013,16(9):1567-1578.

[7]谢文, 孙利民, 魏俊. 附有结构“保险丝”构件的桥墩抗震性能试验研究及其应用[J]. 中国公路学报, 2014(3): 59-70.

XIE Wen, SUN Li-min, WEI Jun. Experimental study on seismic performance of bridge piers with structural fuses and its application on seismic damage control of a super long span bridge[J]. China Journal of Highway and Transport, 2014,16(3): 59-70.

[8]McDaniel C C,Seible F. Influence of inelastic tower links on cable-supported bridge response[J]. Journal of Bridge Engineering, 2005,10(3): 272-280.

[9]Fortney P, Shahrooz B, Rassati G. Large-scale testing of a replaceable “fuse” steel coupling beam[J]. Journal of Structural Engineering, 2007,133(12): 1801-1807.

[10]Vargas R,Bruneau M. Experimental response of buildings designed with metallic structural fuses. II[J]. Journal of Structural Engineering, 2009,135(4): 394-403.

[11]滕军,马伯涛,李卫华,等. 联肢剪力墙连梁阻尼器伪静力试验研究[J]. 建筑结构学报, 2010,31(12): 92-100.

TENG Jun, MA Bo-tao, LI Wei-hua, et al. Pseudo-static test for coupling beam damper of coupled shear wall structure[J]. Journal of Building Structures, 2010,31(12): 92-100.

[12]吕西林,陈云,蒋欢军.可更换连梁保险丝抗震性能试验研究[J].同济大学学报:自然科学版,2013,41(9):1318-1325 .

LÜ Xi-lin, CHEN Yun, JIANG Hua-jun.Experimental study on seismic behavior of “fuse” of replaceable coupling beam[J]. Journal of Tongji University:Natural Science, 2013,41(9): 1318-1325.

[13]纪晓东,马琦峰,王彦栋,等. 钢连梁可更换消能梁段抗震性能试验研究[J]. 建筑结构学报, 2014,35(6): 1-11.

JI Xiao-dong, MA Qi-feng, WANG Yan-dong, et al. Cyclic tests of replaceable shear links in steel coupling beams[J]. Journal of Building Structures, 2014,35(6): 1-11.

[14]吕西林,陈云,蒋欢军.带可更换连梁的双肢剪力墙抗震性能试验研究[J]. 同济大学学报:自然科学版, 2014，42(2): 175-182.

LÜ Xi-lin, CHEN Yun, JIANG Hua-jun. Experimental study on seismic behavior of “fuse” of replaceable coupling beam[J]. Journal of Tongji University:Natural Science, 2014，42(2):175-182.

[15]蒋欢军,刘其舟.可恢复功能剪力墙结构研究进展[J]. 振动与冲击, 2015,34(7): 51-58.

JIANG Huan-jun, LIU Qi-zhou.State-of-the-art of research advances on resilient shear walls[J]. Journal of Vibration and Shock, 2015,34(7): 51-58.

[16]吴浩,吕西林.无粘结后张拉预制剪力墙抗震性能模拟分析[J]. 振动与冲击, 2013,32(19): 176-182.

WU Hao, LÜ Xi-lin. Numerical simulation on seismic performance of unbonded post-tensioned precast shear walls[J]. Journal of Vibration and Shock, 2013,32(19): 176-182.

[17]Park Y J, Ang A H S, Wen Y K. Damage-limiting aseismic design of buildings[J]. Earthquake Spectra, 1987,3: 1-26.

[18]Kunnath S K, Reinhorn A M, Lobo R F. IDARC version 3.0: a program for the inelastic damage analysis of rc structures, technical report NCEER-92-0022[R]. National Center for Earthquake Engineering Research, State University of New York, Buffalo NY., 1992.

[19]魏俊.斜拉桥耗能型辅助墩抗震性能与损伤控制设计方法研究[D]. 上海:同济大学, 2013.

[20]JTG/T B02-01-2008,公路桥梁抗震设计规范[S].