Winkler-Pasternak弹性地基FGM梁自由振动二维弹性解

第一作者蒲育男，硕士,讲师，1984年5月生

通信作者滕兆春男，副教授，1969年8月生

Winkler-Pasternak弹性地基FGM梁自由振动二维弹性解

蒲育1，滕兆春2

(1. 兰州工业学院土木工程学院，兰州730050；2. 兰州理工大学理学院，兰州730050)

摘要：基于二维线弹性理论，建立Winkler-Pasternak弹性地基上功能梯度(Functionally Graded Material,FGM)梁自由振动控制微分方程。假设材料物性沿梁厚度方向按幂律分布，采用微分求积法(Differential Quadrature Method,DQM)数值求解4种不同边界FGM梁自由振动无量纲频率特性。将计算结果与Winkler-Pasternak弹性地基梁对比表明，该分析方法对弹性地基梁自由振动研究行之有效,并考虑边界条件、梯度指数、跨厚比、地基系数对FGM梁自振频率影响。

关键词：Winkler-Pasternak弹性地基；FGM梁；自由振动；无量纲频率；微分求积法

基金项目：国家自然科学基金(11372123)

收稿日期：2014-07-16修改稿收到日期：2014-10-11

中图分类号:O343

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.20.013

Abstract:Based on the two-dimension theory of linear elasticity, the free vibration differential equations for FGM beams resting on Winkler-Pasternak elastic foundations were derived. The material properties were supposed to change continuously along the thickness of the beam according to the power law distribution. Using the differential quadrature method (DQM), the dimensionless natural frequencies of FGM beams under four different boundary conditions were investigated. The formulations were validated by comparing the results obtained with those available in the literature for homogeneous beams on Winkler-Pasternak elastic foundations. The influences of the boundary conditions, material graded index, length-to-thickness ratio and elastic coefficients of foundations on the non-dimensional frequency parameters of FGM beams were discussed.

Two-dimensional elasticity solutions for free vibration of FGM beams resting on Winkler-Pasternak elastic foundations

PUYu1,TENGZhao-chun2(1. College of Civil Engineering，Lanzhou Institute of Technology，Lanzhou 730050，China；2. School of Science, Lanzhou University of Technology, Lanzhou 730050, China)

Key words:Winkler-Pasternak elastic foundation; functionally graded material beam; free vibration; dimensionless frequency; differential quadrature method

弹性地基梁的动力学研究在工程领域有十分重要意义及广泛应用背景，因此已有诸多对其动态响应的研究[1-3]。Rosa等[4]研究弹性地基Euler梁在集中质量块作用下的自由振动。Chen等[5]结合状态空间法(SSM)及微分求积法(DQM)数值研究双参数弹性地基梁的弯曲与自由振动。Ding等[6]用Airy应力函数多项式形式求解弹性地基功能梯度梁在不同边界条件下的动态响应。Ying等[7]用SSM分析简支-简支边界条件的二维弹性地基FGM梁弯曲、自由振动。Alshorbagy等[8]采用FEM分析FGM梁自由振动。Thai等[9]基于高阶剪切梁理论，研究FGM梁弯曲、自由振动。然而对梁自由振动研究大多基于不同的梁理论。

经典梁理论忽略横向剪切变形影响，故仅适用细长梁。而一阶剪切梁理论克服经典梁理论局限性，考虑横向剪切变形影响。本文针对金属-陶瓷功能梯度梁，假设材料性能沿厚度方向呈梯度分布，基于二维线弹性理论，建立Winkler-Pasternak弹性地基FGM梁自由振动微分方程，采用二维DQM数值研究FGM梁自由振动无量纲频率特性，并与各向同性材料梁结果比较。结果显示，该分析方法适用研究弹性地基长梁、短梁自由振动。且DQM较有限差分、有限元、边界元等数值方法具有易收敛、精度高、工作量小等优点。考虑边界条件、梯度指数、跨厚比、地基系数等对FGM梁自振频率影响，获得有益结论。

1控制微分方程及参数的无量纲化

考虑单位宽度金属-陶瓷功能梯度非均匀材料梁见图1，其材料性质沿厚度方向呈梯度分布。梁的上表面为陶瓷(ZrO2)，下表面为金属(Ti-6Al-4V)。弹性模量E，泊松比μ，密度ρ等物性参数是坐标z的函数，用统一式可表示为

(1)

式中：P为梯度指数。

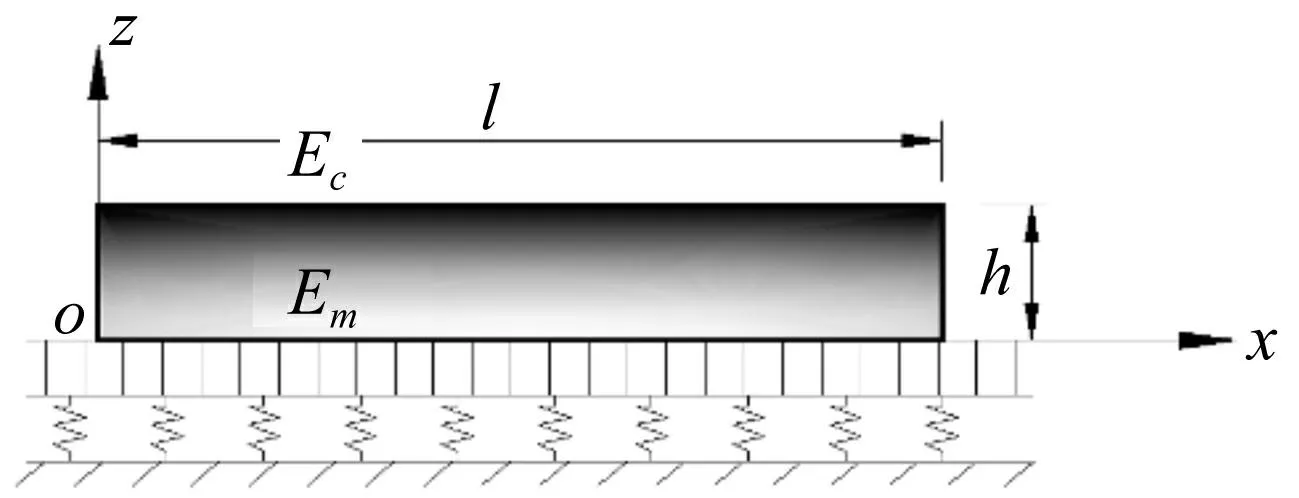
图1　Winkler-Pasternak弹性地基FGM梁 Fig.1 Geometry of a FGM beam on Winkler-Pasternak foundation

设Winkler-Pasternak弹性地基系数分别为kp及kw，x方向位移分量为u，z方向位移分量为w，建立坐标系(图1)。基于二维线弹性理论，物理方程为

(2)

式中：Ci j为材料物性系数，满足关系式为

(3)

将几何方程代入物理方程，再将物理方程代入运动方程得弹性地基FGM梁自由振动微分方程为

(4)

弹性地基梁上下边界条件为

在z=0处

(5)

在z=h处

σz=0，τxz=0

(6)

考虑4种梁的边界条件，即

左端简支-右端简支(S-S)

x=0及x=l处：σx=0及w=0

(7)

左端固支-右端固支(C-C)

x=0及x=l处：u=w=0

(8)

左端固支-右端简支(C-S)

(9)

左端固支-右端自由(C-F)

(10)

无量纲化为

(11)

式中：A为横截面面积；J为惯性矩；ω为固有频率；λ为无量纲频率。

设位移分量为

(12)

式中：I为虚数单位。

将式(11)、(12)代入式(4)及式(5)～式(10)，可得控制微分方程及相应边界条件。

控制微分方程为

(13)

边界条件为:下边界η=0处

(14)

上边界η=1处

(15)

左右边界ξ=0，ξ=1处

固支端(C)

U=W=0

(16)

简支端(S)

(17)

自由端(F)

(18)

2DQM离散化及特征值问题

由文献[10-11]，DQM中梁在x、z方向节点划分算式为

式中：Nξ,Nη分别为ξ及η方向节点总数。

一、二阶导数权系数矩阵满足关系式为

(21)

式中：η与ξ方向权系数矩阵类似，此处省略。

微分方程(13)用DQM离散化后为

式(14)、(15)离散化后分别为

(23)

式中：i=1, 2, …,Nξ； j=1。

(24)

式中：i=1, 2, …,Nξ； j=Nη。

式(16)～式(18)离散化后分别为

(25)

(26)

自由端(F)：

(27)

式中：i=1，Nξ；j=2,3,…Nη-1。

式(23)、(24)与(25)～式(27)对应组合可得4种不同边界条件弹性地基FGM梁，即

左端简支-右端简支(S-S) 弹性地基FGM梁

左端固支-右端固支(C-C) 弹性地基FGM梁

左端固支-右端简支(C-S) 弹性地基FGM梁

左端固支-右端自由(C-F) 弹性地基FGM梁

式(22)与式(23)～式(27)对应联立后便构成不同边界条件Winkler-Pasternak弹性地基FGM梁自由振动边值问题，用分块矩阵形式表示为

(28)

[S]{wb}-Ω2[I]{wb}={0}

(29)

式中：[S]=[Sbb]-[Sbd][Sdd]-1[Sdb]；[I]为单位阵； {wb}为特征向量，可描述弹性地基FGM梁自由振动振型。

3计算结果与分析

算例中FGM梁金属-陶瓷材料物性系数分别为Em=122.7 GPa,μm= 0.288 8,ρm= 4 420 kg/m3,Ec=132.2 GPa,μc= 0.333,ρc=3 657 kg/m3，节点数Nξ=17，Nη= 13，编写MATLAB程序获得式(29)特征值问题无量纲频率。不同地基参数下各向同性材料(p=0)简支梁自由振动基频见表1，其中泊松比μ=0.3，将所得结果与文献[4-5]进行比较知，本文结果与其非常接近，且取较少节点数即能满足精度所需，工作量较小，说明DQM对研究本问题适用性与优越性。当s=1/120，1/15时可视为长梁(Bernoulli-Euler梁)；s=0.2时可视为短梁(Timoshenko梁)。由表1可见，本文方法对长、短梁自由振动分析均适用。

固支-简支(C-S)边界FGM梁在不同厚跨比、不同地基系数下自由振动前三阶无量纲频率见表2。由表2看出，梁的厚跨比s、Winkler弹性系数Kw及剪切地基系数Kp对频率均有影响，所得数值结果可作为工程结构振动分析的参考依据。

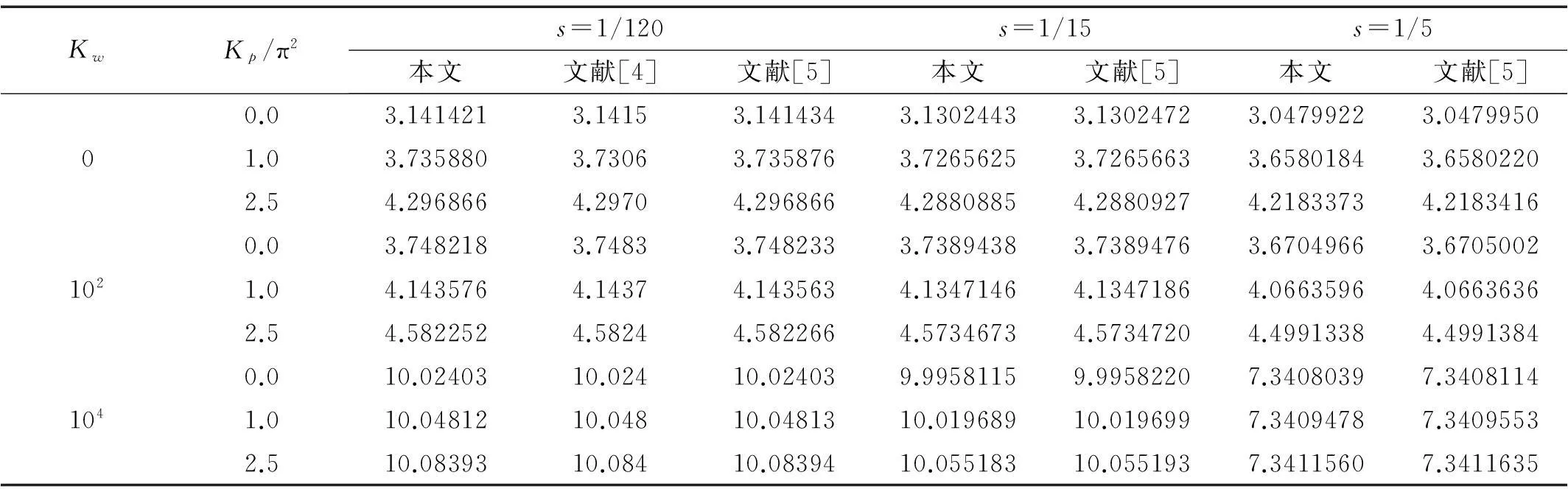
表1　弹性地基简支梁自由振动基频λ 1结果比较(S-S)，μ=0.3

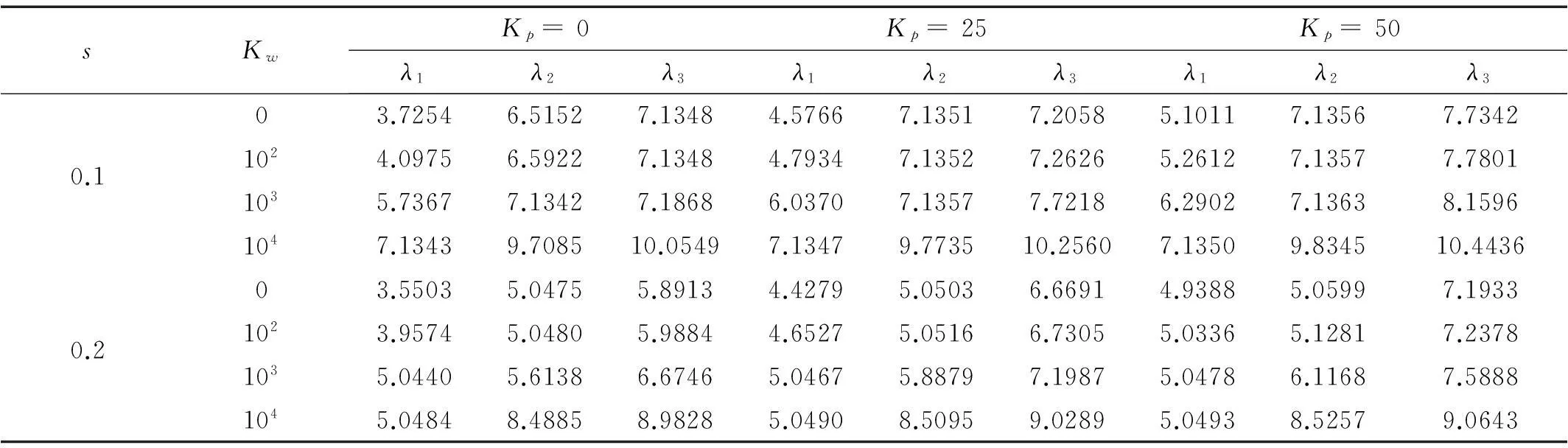
表2　弹性地基FGM梁自由振动前三阶无量纲频率(C-S)，p=1

各向同性梁(p=0)几何参数(跨厚比1/s=l/h)对C-C梁、S-S梁、C-F梁一阶无量纲频率影响见图2，其中泊松比μ=0.3，地基系数Kw=1 000，Kp=10。由图2看出，l/h=[2,50]范围内跨厚比越小其对短梁自由振动频率影响越明显；跨厚比越大其对长梁自由振动频率影响越不明显。1/s≥10时跨厚比对梁频率影响较小，此时可视为细长梁，符合对细长梁的划分界限；但相关报道较少。

弹性地基各向同性梁(p=0)在C-C、C-S、S-S、C-F四种边界下一阶无量纲频率λ1随Winkler地基系数Kw的变化见图3，其中剪切地基系数Kp=10，厚跨比s=0.2，泊松比μ=0.3。由图3可见，Kw=[0,500]范围内，对四种不同边界λ1均随Kw增大而增大，且相同参数时基频由大到小顺序为C-C梁、C-S梁、S-S梁、C-F梁。而剪切地基系数Kp对梁频率影响类似。由此知，系统地基弹性越大频率较高，约束越强频率较大。

Winkler弹性系数Kw与FGM固支-固支(C-C)梁一阶无量纲频率λ1关系曲线见图4。其中Kw=[0,1 000]，Kp=10，s=0.2。显然，对不同梯度指数p，λ1均随Kw增大而增大。

剪切地基系数Kp与FGM简支-简支(S-S)梁一阶无量纲频率λ1关系曲线见图5，其中Kp=[0,100]，Kw=100，s=0.2。由图5看出，对不同梯度指数p，λ1均随Kp增大而增大。

跨厚比1/s与FGM固支-简支(C-S)梁一阶无量纲频率λ1关系曲线见图6，其中1/s=[5,50],Kw=100，Kp=10.由图6看出，对不同梯度指数p，1/s对C-S短梁频率λ1影响明显，而对长梁频率λ1影响不明显。在相同参数下，梯度指数越大频率越小。

不同剪切系数下，FGM固支-固支(C-C)梁Winkler弹性系数Kw与一阶无量纲频率λ1的关系曲线见图7，其中横坐标用指数划分，厚跨比s=h/l=0.2，p=1。由图7可见，在相同参数下，频率λ1先随地基系数Kw增大而增大，当Kw取得较大值时频率基本保持不变(收敛)。表明Kw大到一定值时地基弹性已逐步过渡到“刚性”状态，Kw对λ1影响变小。同样，剪切地基系数Kp对梁自由振动频率关系类似，但相关报道较少。

图2 几何系数跨厚比对一阶无量纲频率影响Fig.2Theeffectofthegeometricalparameteronthefirstnon-dimensionalfrequencyparameterofthebeamonelasticfoundation图3 Winkler地基系数对一阶无量纲频率影响Fig.3Thefirstnon-dimensionalfrequencyparameterversusWinklerelasticcoefficient图4 固支梁一阶无量纲频率与地基系数关系Fig.4Thefirstnon-dimensionalnaturalfrequencyparameterofC-CFGMbeamonelasticfoundationversusKw

图5 简支梁一阶无量纲频率与地基系数关系Fig.5Thefirstnon-dimensionalnaturalfrequencyparameterofS-SFGMbeamonelasticfoundationversusKp图6 几何系数对弹性地基FGM固支-简支梁一阶无量纲频率影响Fig.6Theeffectofthegeometricalparameter1/sonthefirstnon-dimensionalnaturalfrequencyparameter图7 FGM固支梁一阶无量纲频率与地基系数关系Fig.7Thefirstnon-dimensionalnaturalfrequencyparameterofC-CFGMbeamversusKw

图8　固支-简支梁前三阶 无量纲频率与梯度指数关系 Fig.8 The effect of the material graded index p on the first three non-dimensional frequency parameters of the C-S FGM beam

弹性地基FGM梁在固支-简支(C-S)边界下前三阶无量纲频率λ与梯度指数p关系曲线见图8，其中p=[0,100]，Kw=100，Kp=10，s=0.2。由图8看出，λ随梯度指数p增大而减小，p增大到一定值时频率趋于常数。该关系曲线与金属—陶瓷材料物性有关，p=0时FGM梁退化为各向同性陶瓷(ZrO2)梁，p趋于∞时FGM梁视为各向同性金属(Ti-6Al-4V)梁。

4结论

(1)基于二维线弹性理论建立Winkler-Pasternak弹性地基FGM梁自由振动方程，用二维DQM获得不同边界条件下梁自由振动无量纲频率，通过与已有结果比较表明，DQM对弹性地基长、短梁自由振动分析行之有效。

(2)Winkler弹性地基系数与剪切地基系数均对梁振动频率有显著影响。梁自振频率随地基系数增大而增大，地基系数增大到一定值时频率基本不变，地基弹性已逐步过渡到“刚性”状态，即地基弹性越大频率较高；约束越强频率较大。地基系数足够大，频率趋于固定值。

(3)几何系数跨厚比越小对短梁自由振动频率影响越明显，跨厚比越大对长梁自振频率影响越不明显。跨厚比l/h≥10时对梁频率影响较小，此时可视为细长梁(符合力学教材对细长梁的划分界限)。

参考文献

[1]Lee S Y, Kes H Y. Free vibrations of non-uniform beams resting on two-parameter elastic foundation with general elastic end restraints[J]. Computers. Structures, 1990,34: 421-429.

[2]Wang C M, Lam K Y, He X Q. Exact solutions for Timoshenko beams on elastic foundations using Green’s functions [J]. Mechanics of Structures and Machines, 1998, 26(1):101-113.

[3]Ho S H, Chen C K. Analysis of general elastically end restrained non-uniform beams using differential transform [J]. Applied. Mathematic Modelling, 1998, 22(4/5), 219-234.

[4]De Rosa M A, Maurizi M J. The influence of concentrated masses and pasternak soil on the free vibrations of Euler beams-exact solution[J]. Journal of Sound and Vibration, 1998, 212(4):573-581.

[5]Chen W Q, Lu C F, Bian Z G. A mixed method for bending and free vibration of beams resting on a Pasternak elastic foundation[J]. Applied Mathematical Modelling, 2004, 28(10): 877-890.

[6]Ding H J, Huang D J, Chen W Q. Elasticity solutions for plane anisotropic functionally graded beams[J]. International Journal of Solids and Structures, 2007, 44(1):176-196.

[7]Ying J, Lu C F, Chen W Q. Two-dimensional elasticity solutions for functionally graded beams resting on elastic foundations[J].Composite Structures, 2008, 84(3): 209-219.

[8]Alshobagy A E, Eltaher M A,Mahmoud F F. Free vibration characteristics of a functionally graded beam by finite element method[J]. Applied Mathematical Modelling, 2011, 35(1):412-425.

[9]Thai H T, Vo T P. Bending and free vibration of functionally graded beams using various higher-order shear deformation beam theories[J]. International Journal of Mechanical Sciences, 2012, 62(1):57-66.

[10]蒲育, 滕兆春, 房晓林. 圆环板面内自由振动的DQM求解[J]. 振动与冲击, 2013, 32(24): 152-156.

PU Yu, TENG Zhao-chun, FANG Xiao-lin. In-plane free vibration of circular annular plates with differential quadrature method[J]. Journal of Vibration and Shock, 2013, 32(24): 152-156.

[11]Bert C W, Malik M. Differential quadrature method in computational mechanics[J].Appl. Mech. Rev.,1996,49:1-27.