基于HyperWorks的城市客车座椅模态分析

朱晓庆，赵孟阳(青岛大学机电工程学院，山东青岛　266071)



基于HyperWorks的城市客车座椅模态分析

朱晓庆，赵孟阳
(青岛大学机电工程学院，山东青岛266071)

摘要:基于HyperWorks软件建立某客车座椅的有限元模型，并对此座椅模型进行自由模态和约束模态分析，分别得到座椅在两种状态下的模态振型和与之对应的固有频率，并通过模态试验验证模态分析结果的正确性，为城市客车座椅的结构设计提供理论依据。

关键词:城市客车座椅;模态分析;固有频率;振型

随着经济社会的发展，中国的城市化进程不断加快，人口的急剧增加给城市交通系统造成巨大的压力。公共交通系统的发展能够在很大程度上解决城市交通拥堵问题，同时政府大力提倡乘坐公共交通工具出行，因此与人们出行息息相关的公交车受到越来越多的关注。座椅作为城市客车上的重要部件，直接影响乘客的乘坐舒适性。为提高客车座椅的乘坐舒适性，目前大多数学者是从客车座椅的结构和材料方面进行研究［1－2］，理论上的研究较少。本文基于HyperWorks软件建立了某厂家生产的某型号客车座椅的有限元模型，通过模态振型和固有频率从整体上研究座椅的动态特性，以期为客车座椅的结构设计提供理论依据。

1客车座椅结构

选取某厂家生产的RL－F型吹塑客车用座椅，三维模型如图1所示。座椅的外形尺寸为580 mm×440 mm×640 mm，靠背倾角为100°，座椅吹塑厚度为2．5 mm。座椅由靠背、座椅面和支撑骨架组成。靠背、座椅面材料为ABS(丙烯腈－丁二烯－苯乙烯共聚物)工程塑料，弹性模量为2×109Pa，密度为1 050 kg/m3，泊松比为0．39;座椅骨架材料为Q235，弹性模量为2× 1011Pa，密度为7 900 kg/m3，泊松比为0．30。座椅骨架分上下两部分，通过螺栓连接，螺栓安装在骨架上部的方槽中，在没有施加预紧力时螺栓可在方槽中左右移动。座椅骨架上部通过螺栓与座椅相连接，骨架下部通过螺钉与客车车体相连接。

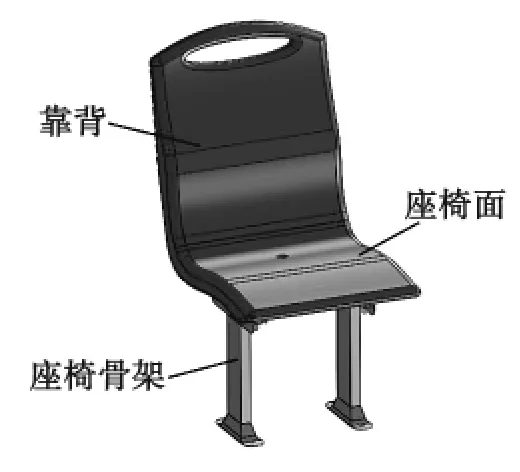
图1座椅的三维模型

对座椅进行有限元分析时，为建立准确的有限元模型，划分出高质量的网格，节约HyperWork的计算时间，需要对座椅模型进行必要的简化［3］，去掉螺栓连接等不影响分析计算结果的小部件，简化之后座椅的有限元模型如图2所示。

图2所示的座椅有限元模型共包括88 093个节点和88 807个单元。有限元模型中采用四边形壳单元( QUAD)、三角形壳单元( TRIA)和混合型壳单元( MIXED)模拟座椅的薄壁件，采用反映主从关系的刚性单元( RBE2)模拟零件间的焊接与螺栓连接。

图2座椅的有限元模型

2客车座椅模态分析

模态分析克服了静态分析的局限性，强调从整体上考虑部件的振动问题［4－6］。在各种阻尼情况下，机械结构上各点对外界激励的响应都可以表示成由固有频率、阻尼比和振型等模态参数组成的各阶模态振型的叠加［7］。客车行驶过程中，座椅会受到外界振源的激励，如路面激励、发动机激励等，如果这些振源的激振频率接近座椅的固有频率，就会引起共振，产生剧烈振动，这不仅会对座椅造成破坏，影响座椅的使用寿命，剧烈的振动还会影响乘客的乘坐舒适性。

在外界激励的作用下，座椅的振动微分方程［8－9］为:

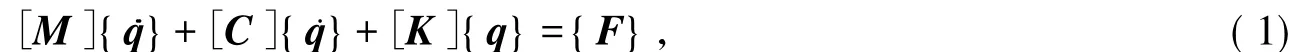
式中: M为质量矩阵; C为阻尼矩阵; K为刚度矩阵; { q}为客车座椅振动的位移向量; { F}为座椅受到的外界振源激励向量。

2．1自由模态分析

若式( 1)中的外界激励向量{ F} = 0，在非零初始条件下，方程有非零解，此时座椅处于自由振动状态。因为没有外力的作用，此微分方程的解便能够反映自由状态下座椅结构本身固有的模态振型和与之对应的振动频率。在求解座椅的固有频率的模态振型时，可以忽略阻尼项，进而得到系统无阻尼自由振动的微分方程为:

系统的特征值方程为:

式中: wi为方程的特征值; {φ}( i)为对应特征值的特征向量。

通过HyperWorks有限元软件计算分析得出座椅在自由状态下的前8阶固有频率分别为17. 00、23. 42、49. 92、65. 12、66. 75、78. 55、82. 47、91. 21 Hz。座椅在自由状态下的前6阶模态振型图［10］如图3所示(图3中单位为Hz)。

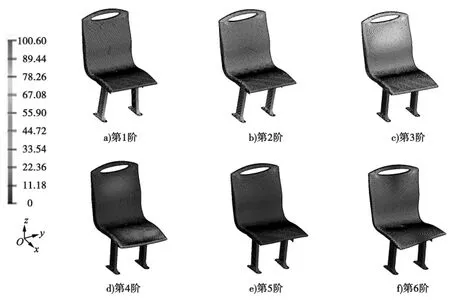
图3座椅的自由模态振型

2．2约束模态分析

自由模态分析反映的是座椅结构本身固有的动态特性，而约束模态分析是在座椅结构上施加正确的约束，约束座椅的某些自由度，反映的是机体结构的实际工作情况，更具有研究价值。

2．2．1约束

在正常工作状态下，该座椅安装在客车的地板上，座椅骨架与客车地板通过4个螺钉相连接。根据实际安装情况，在4个螺钉连接部位施加约束，约束其6个自由度。

2．2．2约束模态结果分析

通过HyperWorks有限元软件计算分析得出座椅在施加约束状态下的前8阶固有频率分别为17. 19、30. 57、59. 83、64. 27、65. 82、82. 87、84. 84、90. 73 Hz。图4为座椅在约束状态下的前6阶模态振型图(图4中单位为Hz)。

约束状态下座椅的第1阶模态的振动形式如图4a)所示，固有频率为17．19 Hz，表现为座椅整体沿y轴方向的弯曲振动。第2阶模态的振动形式如图4b)所示，固有频率为30．57 Hz，表现为座椅靠背上部沿x轴方向的弯曲振动。第3阶模态的振动形式如图4c)所示，固有频率为59．83 Hz，表现为座椅面和前端沿z轴方向的弯曲振动和座椅靠背沿x轴方向的弯曲振动，座椅面的振幅较座椅靠背大。第4阶模态的振动形式如图4d)所示，固有频率为64．27 Hz，表现为座椅面和靠背的扭转。第5阶模态的振动形式如图4e)所示，固有频率为65．82 Hz，表现为座椅面前端沿z轴方向的弯曲振动和座椅靠背沿x轴方向的弯曲振动，座椅靠背的振幅较座椅面大，且座椅靠背正面和背面振动方向相反。座椅的第6阶模态的振动形式如图4f)所示，固有频率为82．87 Hz，表现为座椅面和座椅靠背的扭转，扭转方向与第四阶模态振型扭转方向相反。

通过客车座椅的模态分析可以看出，座椅从第1阶模态到高阶模态依次经过了刚性振动阶段、整体弹性振动阶段和局部弹性振动阶段，且不同频率下的模态振型不同，高频模态振型相当复杂。在不同的约束状态下，座椅的同阶固有频率比较接近，但是模态振型的振动形式差别很大。同时，座椅的某些部位(如座椅面)振动幅度较大，发生共振时容易使座椅产生破坏。根据相关资料［11－12］，由路面不平度引起的激励频率多在20 Hz以下，且方向多为垂直振动，因此不会引起座椅的共振。城市客车发动机正常工作频率为16～50 Hz，可见，在约束状态下，此座椅前2阶模态的固有频率在此频率范围内。城市客车在起步时，发动机转速较低，激励频率也较低，更容易接近座椅的第1阶固有频率( 17. 19 Hz)，从而引起座椅的共振。这也是在某些情况下，城市客车在起步时空载座椅产生剧烈振动的原因。

3模态分析的试验验证

为了验证座椅有限元模型建立和分析的正确性，需要对座椅进行模态试验验证［13］。试验中对座椅自由模态分析和约束模态分析的试验验证采用不同的安装方式［14－15］。在自由模态试验中，座椅采用两根软绳吊装;在约束模态试验中，根据实际情况，将座椅安装在城市客车地板上，骨架的固定方式如图5所示。试验采用两点激励、多点测取的方法，激励使用BK8202型力锤，测量系统采用KISTLER8702B50型加速度传感器和与之匹配的电荷放大器。试验测试系统构成如图6所示。根据有限元分析的结果和座椅实际安装情况，选择振动幅度较为明显的26个点作为加速度传感器的安装位置点，选择座椅骨架下端作为激励力锤的安装位置点。激振点和传感器安装位置点如图7中白色点所示。

图5试验中座椅骨架的固定方式

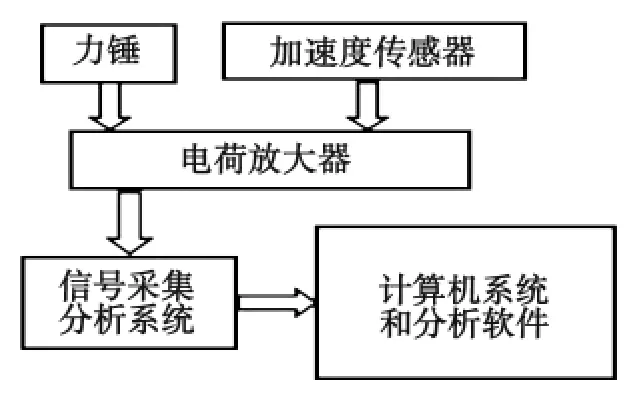
图6试验测试系统构成

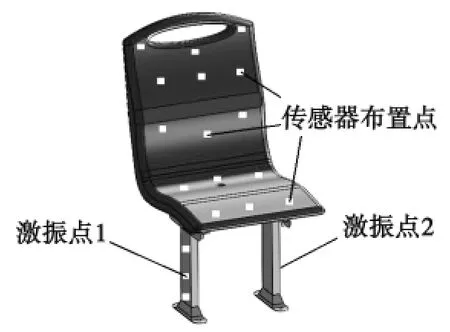
图7传感器布置点分布图

表1、2分别为2种状态下试验结果与计算结果的比较。通过表1、2中所测得的数据可以看出，最大相对误差为13．22%，模态试验所得到的结果与有限元软件计算所得到的结果基本一致，验证了所建模型和有限元分析的准确性。但是实验频率大都小于有限元计算频率，原因是有限元模型省略了对计算结果影响较小的连接部件，如螺栓连接，造成了固有频率偏低。表1、2中也存在个别试验频率大于计算频率的情况，但不会对整体试验结果产生影响。

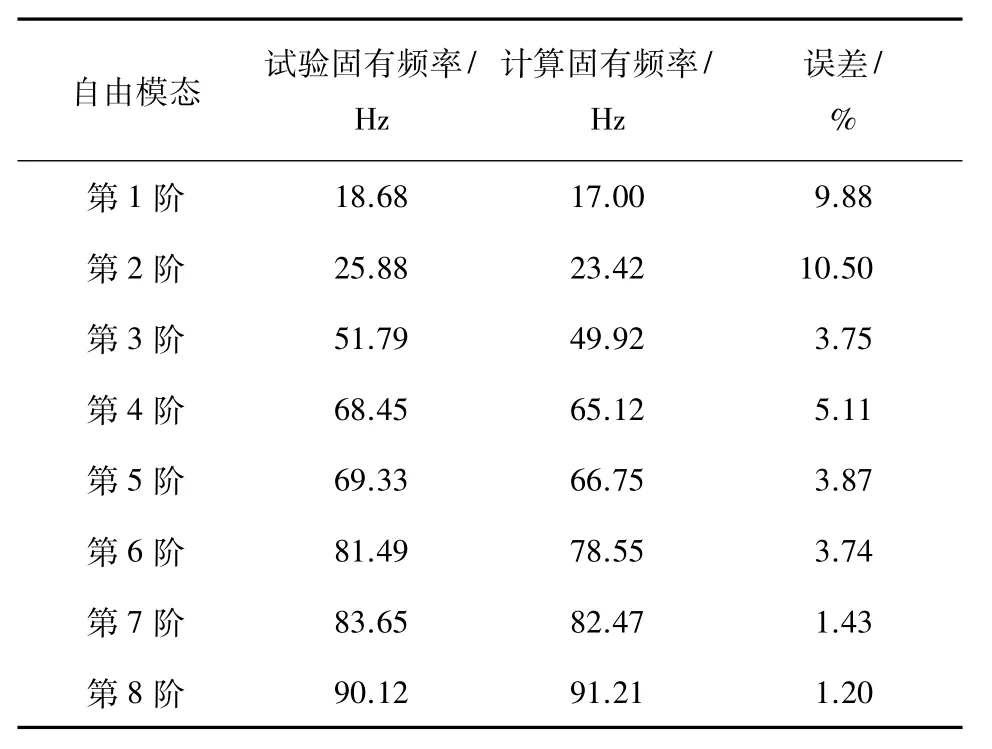
表1自由模态试验结果

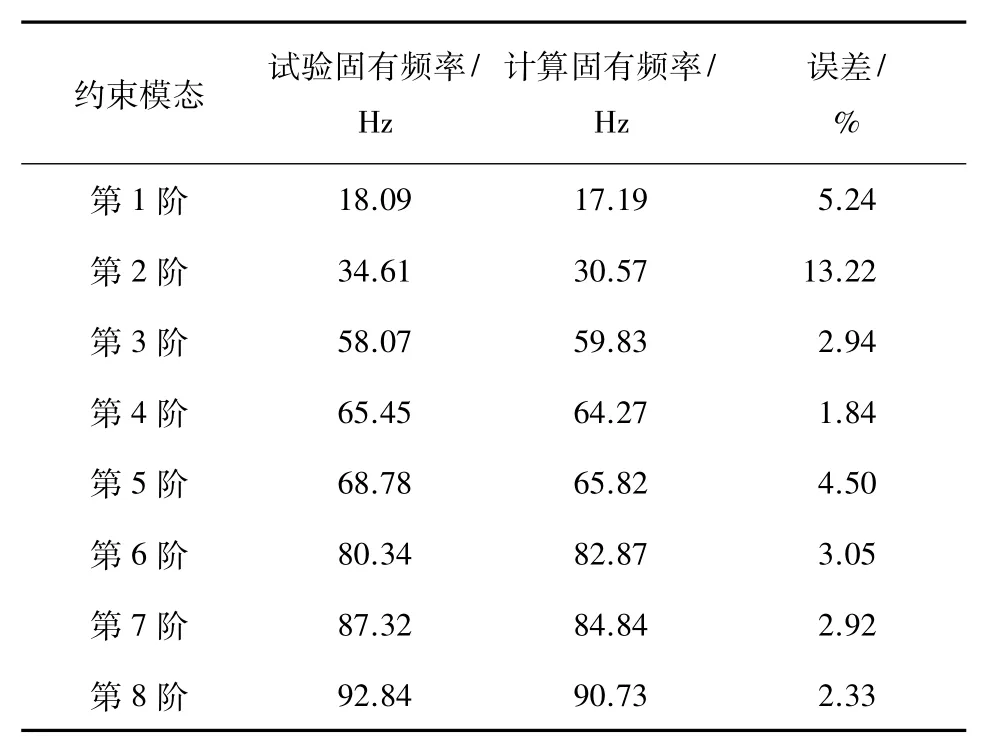
表2约束模态试验结果

4　结论

1)基于HyperWorks软件，建立某城市客车座椅的有限元模型，计算分析得到该座椅在两种状态下的前8阶固有频率和模态振型，座椅从第1阶模态到高阶模态依次经过了刚性振动阶段、整体弹性振动阶段和局部弹性振动阶段。城市客车低速行驶时，发动机的工作频率与座椅的第1阶固有频率接近，座椅容易产生剧烈振动。

2)模态试验所得座椅的固有频率与座椅自由模态分析和约束模态分析固有频率的有限元计算结果基本一致，验证了所建模型和有限元分析的准确性。

3)本文分析结果可作为分析座椅结构动力响应和其他动力特性问题的基础，可帮助设计人员在后续设计中避开容易产生振动的频率范围或减小在这些频率上的激励，从而减少共振现象的发生，同时也为座椅的结构设计和改进提供了理论基础。

参考文献:

［1］李娟，李辉，王小庆．城市客车乘客座椅的舒适性分析和改进设计［J］．中国西部科技，2010，9( 14) : 32－33．

［2］叶彪．客车乘客座椅的乘坐舒适性［J］．客车技术与研究，2003，25( 4) : 21－23．

［3］包丽，仝建．结合模态分析的VMC850E加工中心主轴动态误差研究［J］．制造技术与机床，2015( 1) : 72－75．

［4］陈德玲，陈效华，张建武．三段式大型客车车架模态分析［J］．南京理工大学学报，2004，28( 4) : 400－403．

［5］徐宏海，李晓阳．带超长滚珠丝杠的立式玻璃磨边机砂轮架模态分析［J］．振动与冲击，2013，32( 18) : 189－194．

［6］ROESSET J M，WHITMAN R V，DOBRY R．Modal analysis for structures with foundation interation［J］．Journal of the Structural Division，2014，100: 476－478．

［7］蒋红旗，王繁生．起重机吊臂结构有限元模态分析［J］．农业机械学报，2006，37( 3) : 20－22．

［8］李德源，叶枝全，包能胜，等．风力机旋转风轮振动模态分析［J］．太阳能学报，2004，25( 1) : 72－77．

［9］叶友东，周哲波．基于ANSYS直齿圆柱齿轮有限元模态分析［J］．机械传动，2006，30( 5) : 63－65．

［10］张义民．机械振动［M］．北京:清华大学出版社，2006．

［11］阮仁宇，谭继锦，魏洪革．基于发动机激励下的客车骨架动态特性分析［J］．湖北汽车工业学院学报，2011，25( 1) : 14－18．

［12］木标，王浩，蒋成武．客车车身骨架动态特性分析［J］．山东交通学院学报，2011，19( 2) : 9－12．

［13］黄超群，来飞．重型货车车架模态分析与试验研究［J］．山东交通学院学报，2011，19( 1) : 1－4．

［14］谢小平，韩旭，陈国栋，等．某商用车驾驶室白车身模态分析［J］．湖南大学学报(自然科学版)，2010，37( 5) : 24－30．

［15］HOOPER J M，MARCO J．Experimental modal analysis of lithium-ion pouch cells［J］．Journal of Power Sources，2015，285: 247－259．

(责任编辑:杨秀红)

Modal Analysis of City Bus Seat Based on HyperWorks

ZHU Xiaoqing，ZHAO Mengyang
( College of Mechanical and Electrical Engineering，Qingdao University，Qingdao 266071，China)

Abstract:In this paper，the finite element model of bus seat is established by the HyperWorks software．Then，the seat model is analyzed through the free mode and constrained mode．The modal vibration modes are obtained in the two conditions and the corresponding natural frequencies respectively．Finally，the analysis result is verified to be corrected by the modal experiments，which provides theoretical basis for the structure design of city bus seat．

Key words:city bus seat; modal analysis; natural frequency; vibration mode

作者简介:朱晓庆( 1989—)，男，山东青岛人，硕士研究生，主要研究方向为汽车动态仿真与控制技术．

收稿日期:2015－03－25

DOI:10．3969/j．issn．1672－0032．2015．02．002

文章编号:1672－0032( 2015) 02－0006－05

文献标志码:A

中图分类号:U463．836; U469．103