真空浇注过程控制技术研究

金　杨　税远强　段红玲(二重集团(德阳)重型装备股份有限公司，四川618013)



真空浇注过程控制技术研究

金杨税远强段红玲
(二重集团(德阳)重型装备股份有限公司，四川618013)

摘要:通过理论计算、数值模拟和现场实际相结合的方式，对兑钢过程、真空浇注过程控制进行了分析研究，建立了数学模型，用于现场浇注过程的精确控制，并在生产实践中得到了很好的验证。

关键词:真空浇注;过程控制;数学模型;数值模拟

随着国家核电和石化工业的发展，用于锻件产品的超大型钢锭的需求也逐渐增多，比如CAP1400百万千瓦级常规岛发电机转子就需要650 t钢锭进行锻造，此类产品的性能和无损检测要求极高，也在客观上增加了大型钢锭生产的难度［1～3］。为适应市场的需求，我公司近年来钢锭的等级由200 t级逐渐提升至600 t级，而随着产品自身质量要求的提升，对于钢锭浇注过程控制的要求也在不断提升。本文通过理论计算、数值模拟和现场实际相结合的方式，对兑钢过程、真空浇注过程控制进行了分析和研究，建立了数学模型，用于现场指导，并取得了较理想的成果。

1　真空浇注过程数学模型的建立

超大型钢锭的浇注过程一般需要多包浇注，若钢包衔接不及时则有可能导致断浇，或者将中间包的顶渣冲入钢水内被水口处的钢流吸入钢锭模内形成夹杂物。为此，就需要精确掌握中间包的浇注速度和浇注时间，并以此控制大包的衔接。本文将真空浇注过程简化为钢水在真空条件下由水口流出的过程，利用伯努利方程对真空浇注过程进行描述［4］如下:

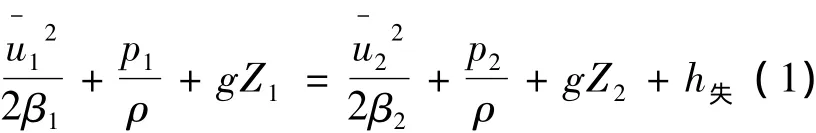
通过换算及简化，可以得出:

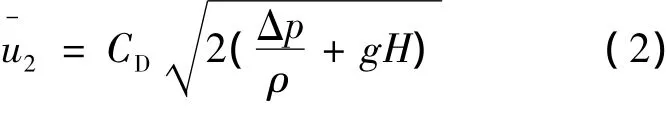
钢水通过水口处的质量流量为:

式中A2为水口的截面积，τ为浇注时间。

当流出钢水量为dM时，中间包内钢液面下降dH，则有

依据式( 2)～式( 4)可以推导出:

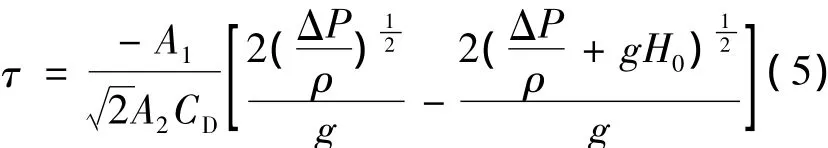
当前工艺条件下，除了流尽前一段时间为层流状态，其余全为紊流状态，此时β2= 1，依据Re和A1/A2值，取K = 0．075，计算得出CD= 0．96。将实际数据带入式( 2)、式( 5)可得:

τ= 3．92×( 13．48 + 9．81H)1－14．37 ( 6)

2式中τ为浇注时间，单位为min; u－为浇注速度，单位为m/s; H为钢液面高度。

使用公式对现场A、B、C三种锭型浇注时间的实际值与理论值进行对比，结果如表1所示。

表1　不同钢锭实际浇注时间与理论计算浇注时间比较结果Table 1　Compared results of actual pouring time and theoretical calculated pouring time for different ingots

考虑到浇注控流等影响，可以说，公式对浇注时间的判断符合现场实际过程，浇注速度也均在工艺要求范围之内，因而可以说，式( 6)和式( 7)可以用于指导现场生产。

2　浇注终了时间的控制

中间包浇注将近流空时，为防止水口处真空抽力将钢液面上的钢渣抽入钢锭模中，需要提前关闭水口，结束浇注。为精确掌握结束浇注的时间，防止下渣，对不同水口直径的中间包临近终了时的钢液流动进行了数值模拟计算。

2．1计算模型及条件

以现场实际中间包为几何模型，简化后建立数学模型，利用CFD计算软件fluent进行数值模拟计算。为节省计算时间，仅对中间包包底部进行计算，由于计算中最关心的是下渣时刻前后的流动特性，而之前的流动变化很缓慢，因此只要下渣前有一段时间让流动充分发展，则下渣的情况则是真实可靠的。图1、图2即为计算用几何模型和网格。原点取在中间包底面中心处，Z轴正方向为竖直向上，计算网格采用六面体及四面体结合的网格，在包底及水口处细化网格以提高计算的精确性。计算中材料物性参数［5］见表2，不同水口直径计算用节点数量和网格数量见表3。

利用CFD软件自带的非稳态模型、k-ε湍流模型以及VOF多相流模型对浇注过程进行模拟计算研究。计算中假设中间包内由钢水和钢渣组成，其高度各不相同，钢渣之上部分为空气，在浇注过程中水口始终处于全开状态，计算中未考虑钢水对水口的冲刷。计算边界条件是压力入口为本地大气压强，出口条件为工艺要求的真空度。

2．2计算结果

图3～图9分别为不同直径水口的下渣时刻前后钢—渣的组分浓度云图。下渣时刻中间包内钢液高度见表4。

根据表4结果并结合计算中保存的动画，可得出，在当前工艺条件下，水口直径的逐渐增大，下渣时的液面高度逐渐下降，可以理解为随着水口截面增加，则水口的抽力逐渐减小所致。为防止下渣，在浇注终了阶段，应保持中间包内存在至少80 mm高度的钢水富余量。

表2　钢液和钢渣的物性参数Table 2　Physical parameters of molten steel and slag

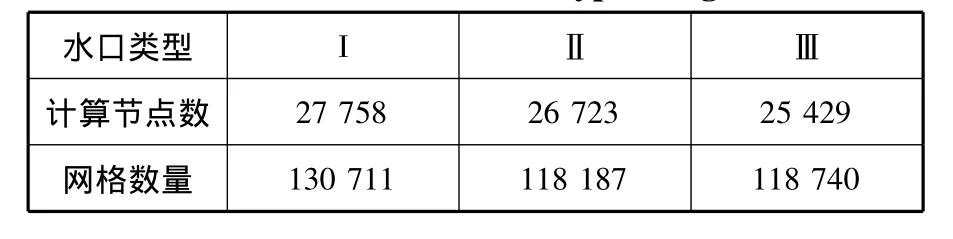
表3　不同水口直径计算用节点数量和网格数量Table 3　Number of nodes and grids used for calculation of different types of gate

图1　计算用几何模型Figure 1　Geometric modeling used for calculation

图2　计算用网格Figure 2　 Grids used for calculation

图3　下渣前钢渣的组分浓度云图( I类水口)Figure 3　Composition concentration nephogram of slag before roughing slag ( I type gate)

图4　初下渣时钢渣的组分浓度云图( I类水口)Figure 4　 Composition concentration nephogram of slag at the beginning of roughing slag ( I type gate)

图5　下渣前钢渣的组分浓度云图(Ⅱ类水口)Figure 5　Composition concentration nephogram of slag before roughing slag ( II type gate)

图6　初下渣时钢渣的组分浓度云图(Ⅱ类水口)Figure 6　 Composition concentration nephogram of slag at the beginning of roughing slag ( II type gate)

图7　下渣前钢渣的组分浓度云图(Ⅲ类水口)Figure 7　Composition concentration nephogram of slag before roughing slag ( III type gate)

图8　初下渣时钢渣的组分浓度云图(Ⅲ类水口)Figure 8　Composition concentration nephogram of slag at the beginning of roughing slag ( III type gate)

图9　计算用网格模型Figure 9　 Grid model used for calculation

表4　下渣时刻中间包内钢液高度Table 4　The height of molten steel in the tundish at the moment of roughing slag

图10　流场稳定时渣、钢组分云图( H =2．7 m)Figure 10　Composition nephogram of slag and molten steel when the flow field is stable ( H =2．7 m)

图11　流场稳定时渣、钢组分云图( H =1．5 m)Figure 1　Composition nephogram of slag and molten steel when the flow field is stable( H =1．5 m)

图12　流场稳定时渣、钢组分云图( H =1．1 m)Figure 12　Composition nephogram of slag and molten steel when the flow field is stable( H =1．1 m)

图13　流场稳定时渣、钢组分云图( H =0．8 m)Figure 13　Composition nephogram of slag and molten steel when the flow field is stable( H =0．8 m)

3　多包合浇过程，中间包最低钢液面的控制

在浇注超大型钢锭时，一般需要多包合浇，此时顶部钢流的冲击、底部水口处的抽力以及包底包壁的反射等共同对钢液产生流动作用，钢液的流动较为复杂，顶渣卷入的几率较大，此时就需要钢液有一定的深度，使得顶渣卷入后有充分的时间上浮，而不是被水口抽走，进入钢锭模中形成夹杂物。为确定大包兑入时中间包的极限钢液面高度。按现场实际工况使用FLUENT软件进行模拟计算，计算边界条件是速度入口为大包兑入的速度，压力出口条件为工艺要求的真空度。计算模型及网格如图9所示。

3．1计算结果

图10～图13分别为不同水口直径的下渣时刻前后钢—渣的组分浓度云图。

从以上不同高度钢液面流动稳定时的钢、渣组分云图和保存的动画可以看出:

( 1)钢液面深度由0．8 m增加至1．5 m时，钢液冲击对渣面的影响逐渐增大，渣面中间的亮面逐渐增大。而当钢液面深度由1．5 m增加至2．7 m时，亮面呈现逐渐缩小的趋势，观察动画中渣面波动的规律与此相同。其原因应该是大包钢流对液面冲击力、水口抽力、中间包包壁包底反射等共同作用的结果，随着液面高度的变化，以上各作用力不断变化，反映出如上规律。

( 2)从减轻渣面波动，减少钢液二次氧化以及钢液卷渣几率等方面考虑，多包浇注换包时，中间包内钢液面极限高度应为0．8 m，但是存在较大的下渣风险，钢液面在1．5 m时顶渣进入钢锭模的几率较小。根据以上结论，结合式( 6)、式( 7)，可以确定现场多包浇注时允许最大间隔时间为8 min。

利用以上结论在现场生产过程中进行实践，2014年以来车间冶炼的超大型真空钢锭的现场过程控制以及后续的产品质量均取得了令人满意的结果。

4　结论

( 1)通过理论计算并结合现场实际，建立了符合现场实际的浇注过程数学模型:

( 2)在当前工艺下，在浇注末期应在中间包内保持80 mm高度的钢水富余量以防止钢渣流入。

(3)对大包兑钢时中间包内的钢渣卷混情况进行模拟计算，得出多包合浇过程汇总，允许最大换包时间不得超过8 min，否则钢渣进入钢锭模内的风险较大。

参考文献

［1］高建军，巴钧涛．超大型钢锭制造技术研究［J］．大型铸锻件，2013( 2) :7－10．

［2］Yasuto Ikeda，Koji Morinaka，Tomohiro Muraoka．Recent Technological Progress on Large Ingots for Rotor Forgings［J］．18th international Forgemasters Meeting Proceedings．2011: 166－169．

［3］Yasuto Ikeda，et al．JCFC改进的真空铸造技术的开发．二重内部资料．

［4］高家诚．传输原理［M］．重庆大学内部教材．

［5］田陆，王杉．基于Fluent的钢水连铸下渣振动的初步研究．第十五届全国炼钢年会论文集，2008:779－784．

编辑李韦萤

Research on Vacuum Pouring Process Controlling Technology

Jin Yang，Shui Yuanqiang，Duan Hongling

Abstract:By combining the theoretical calculation and the numerical simulation with the actual conditions on site，the process control of mixing molten steel and vacuum pouring have been analyzed and studied．A mathematical model used for precise control of site pouring process has been established and verified during the production practice．

Key words:vacuum pouring; process control; mathematical model; numerical simulation

收稿日期:2014—10—31

文献标志码:B

中图分类号:TF775+．4