薛定谔方程与光学傍轴波动方程的相似性及airy光束①

薛定谔方程与光学傍轴波动方程的相似性及airy光束①

董梅峰宋新祥韩巧丽朱化凤刘 冰

[中国石油大学(华东)理学院山东 青岛266580]

*中国石油大学教学研究改革项目资助,项目编号:JY-A201402

摘 要：薛定谔方程是大学物理教学中量子物理部分最基本的方程，而光学中如何得到无衍射光束是近年来光学研究领域的一个重要课题，文中通过薛定谔方程和光学傍轴波动方程之间的数学对应关系，得到了一种无衍射airy光束．教学结果发现，在大学物理教学中通过与上述研究性课题的联系，大大提高了学生的科学研究素质及其各方面的能力．

关键词：大学物理薛定谔方程airy光束

作者简介：董梅峰(1973-)，女，硕士，讲师，从事信息光学的研究和大学物理的教学工作.

收稿日期：(2015-04-28)

大学物理讲解的是自然界中所有物质的最基本、最普遍的客观运动规律以及物质基本结构的科学，因此在大学物理教学中要把知识点与客观实际相结合，可以培养学生的科研创新能力、动手实践能力和动脑思考探索能力，从而培养学生的科学研究素质．

薛定谔方程是大学物理教学中量子物理部分最基本的方程，而它在实际科学研究中的作用，在大学物理中涉及的不多.文中通过薛定谔方程和光学傍轴波动方程的相似性，把薛定谔方程和光学中的一个研究性课题联系起来，让学生更深入地了解了薛定谔方程的应用，同时也对光学中airy光束的特点和应用有了一定的了解，并通过计算机软件把airy光束模拟仿真出来，从而大大提高了学生的学习兴趣.

1薛定谔方程和傍轴波动方程

一维自由粒子的薛定谔方程[1]为

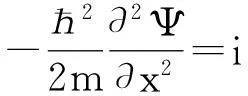
(1)

一维自由空间傍轴光波的波动方程[2]为

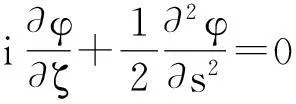
(2)

公式中φ是光波的包络，s是无量纲的横坐标，ζ是归一化传输距离. 其中

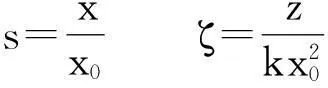
(3)

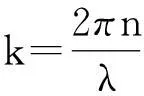
(4)

比较式(1)和式(4)，数学形式是一致的，因此有着相同形式的解.

2airy光束

airy光束是无衍射光束，它是薛定谔方程的一个精确解，这最初是由Berry和Balazs于 1979 年在理论上证明的[3].因此式(4)也有相应的无衍射airy函数解.令

φ(x,z)=Ai[f1(x,z)]exp[f2(x,z)]

(5)

由于是无衍射解，所以上式中f1(x,z)=αx+f(z)，即在z=0的初始状态下，式(5)为

φ(x,0)=Ai(αx)

(6)

将式(6)代入式(4)得

(7)

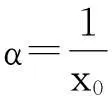
3airy光束的计算机模拟

airy光束作为一种无衍射光束，它在光学微操纵[4]、电子加速[5]等领域具有重要应用，因此对airy光束的研究是光学领域一个重要的课题.在大学物理的教学中引入airy光束简单的计算机模拟，形象地向学生展示airy光束的同时，也培养了学生应用软件编写程序的能力.下面是对airy光束简单的计算机模拟情况.

3．1理想的无衍射airy光束的计算机模拟

计算机模拟过程中，任意横向尺度x0=0.1mm,λ=632.8nm,折射率n=1；采用MATLAB[6]软件.计算机模拟的一维airy光束沿z 轴传输过程如图1所示， 其中纵坐标是airy光束在z轴方向的传播距离，横坐标是airy光束在x轴上的横向光场分布，x轴上中央横向光场分布称为主瓣，中央的左边光场分布称为旁瓣.由图1可以看出，airy光束在x轴上的主瓣尺寸在传播过程中没有展宽，因此airy光束是无衍射光束；另外也可以看出，airy光束在x轴上的主瓣随着在z轴上传播距离的增加发生了横向偏移，这类似于粒子在重力的作用下做平抛运动所产生的抛物线形轨迹，airy光束的这一传输现象被称为“横向自由加速现象”.

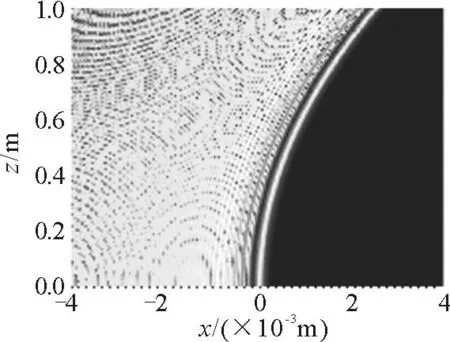
图1　 airy光束的传输

图2是二维airy光束分别在z=0和z=0.6m处光强分布情况的三维立体图，其纵坐标为归一化能量.

图3是二维airy光束分别在z=0和z=0.6m处光强分布的平面图.由图2和图3均可以看出，在z=0和z=0.6m处的airy光束主瓣分布基本相同，也就是主瓣尺寸没有展宽；同时也可以看出主瓣光场表现出了沿着 x-y 轴对角线加速的特性；另外，图2和图3也表现出了随着传输距离的增加，airy光束旁瓣构成的“尾翼”也随之变大.

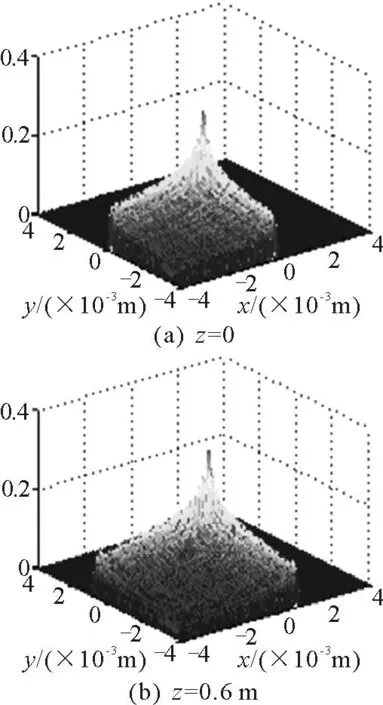
图2　二维 airy光束在z=0和z=0.6 m处的能量分布

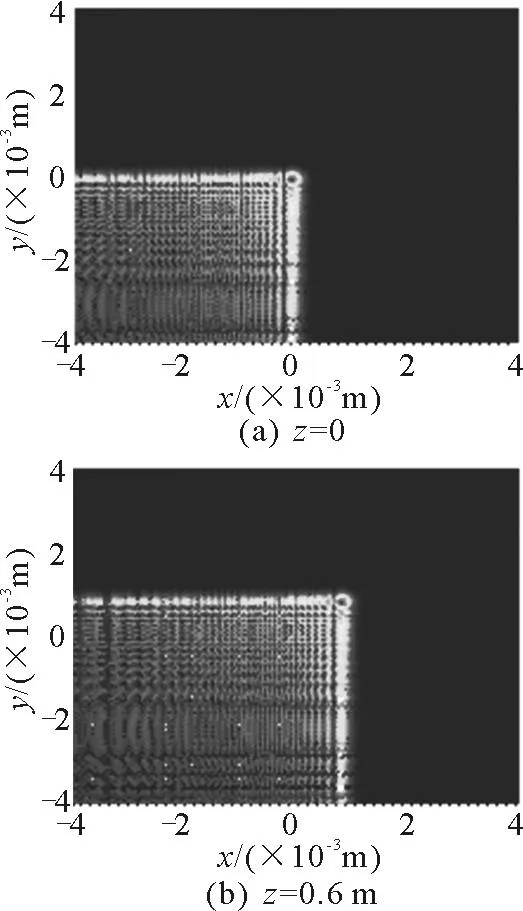
图3　二维 airy光束在z=0和z=0.6 m处能量分布的平面图

airy光束由于具有上述的无衍射特性和自由加速特性，从而引起了很多研究人员的兴趣.然而如何解释airy光束的自由加速特性，文献[7]给出了等效性解释，认为恒定场中airy波包的横向加速行为可以看作是驻波横向平面内的自由落体者眼中所观察到的，因为自身惯性缺失而造成横向上的加速现象.上述式(7)表示的airy光束是平方不可积的，也就是在理论上携带无限大的能量，因此，上述airy光束被认为是理想的airy光束，理想的airy光束无论传输多远都可以保持横向自由加速和无衍射，就像自由落体的物体在不受阻力和摩擦力的情况下一直保持重力加速一样.

以上的理论推导和计算机模拟是对理想airy光束而言的，这样的无衍射airy光束在实际中并不存在，光束在传播过程中都会产生衍射，如果“截止”孔径超出了理想传输不变场的空间要求，衍射会被控制在一定的范围内；另外，上述无衍射airy光束携带无限大的能量，因此理想的airy光束在物理上没有实际物理意义.为了使airy光束具有实际物理意义，下面引入有限能量airy光束.

3．2有限能量airy光束的计算机模拟

要得到有限能量airy光束，只需要在理论上作如下处理.即当z=0时，也就是初始状态下，令

φ(x,0)=Ai(αx)exp(bx)

(8)

其中b为衰减系数.把式(8)代入式(4)得有限能量的airy光束为

(9)

上述参数不变的情况下，图4(a)、(b)分别是衰减系数b=0.05和b=0.1时有限能量一维airy光束的传输情况.由图4可知，与图1无限能量airy光束相比，有限能量airy光束在传输过程中能量明显衰减；由图4也可以看出衰减系数越大，有限能量airy光束的能量衰减得越快；同时也可以看出当衰减系数b=0.05时，airy光束在传输到0.8m处时其强度仍清晰可见，这就说明了有限能量airy光束具有近似无衍射特性，因此有限能量airy光束具有重要的应用价值.

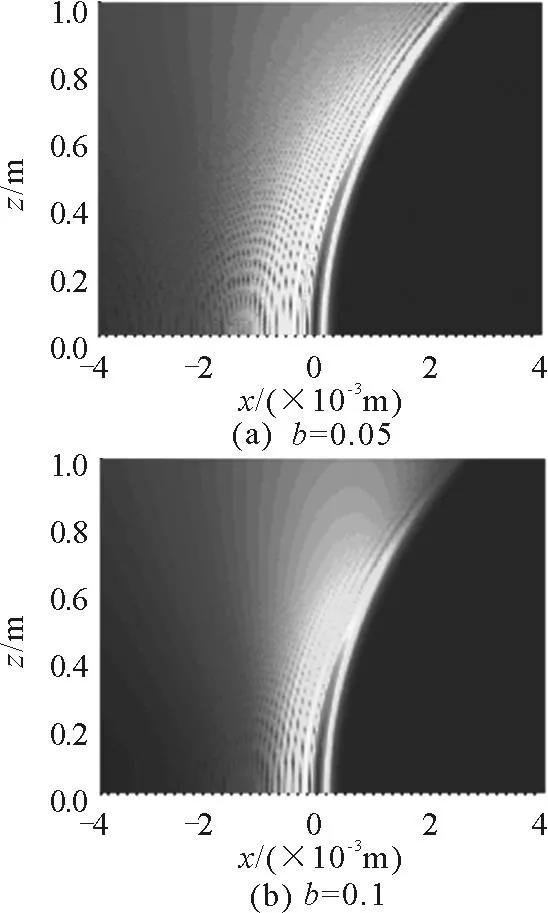
图4　有限能量一维 airy光束的传输

图5(a)、(b)分别是当衰减系数b=0.05时，二维有限能量airy光束在z=0和z=0.6m处的光强分布情况，由图可以看出，在z=0和z=0.6m处有限能量airy光束的主瓣光强变化不大，因此在 z=0和z=0.6m之间的距离内，有限能量airy光束具有近似无衍射特性.

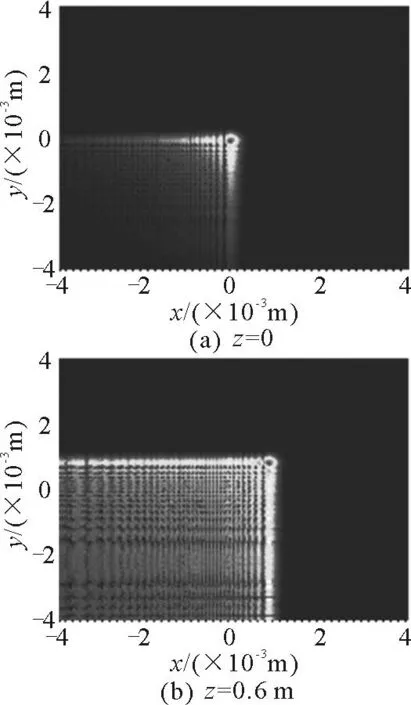
图5　二维 airy光束在z=0和z=0.6 m处能量分布的平面图

4结论

文中通过薛定谔方程和傍轴波动方程的相似性，得出了无衍射airy光束，在此基础上得出了有限能量airy光束，并通过计算机模拟出了相关的结果.在大学物理量子物理部分的教学过程中，进行以上相关知识的拓展延伸，让学生从更深层次上理解了薛定谔方程，也使他们了解了当前的一个科学研究课题，通过理论推导和计算机程序模拟，大大提高了学生的科学研究素质，也提高了学生学习大学物理的兴趣.

参 考 文 献

1李元成.大学物理学.北京：中国石油大学出版社，2011

2G.A.Siviloglou and D.N. Christodoulides,Opt. Lett. 32,2447(2007)

3M.V.Berry,N.L.Balazs.Nonspreadingwavepackets.Am.J.Phys.,1979,47(3):264～267

4Cao R,Yang Y,Wang J,et al.Microfabricated continuous cubic phase plate induced Airybeams for optical manipulation with high power efficiency. Applied Physics Letters,2011,99(26): 261106

5LiJX,FanXL,ZangWP,TianJG,VacuumelectronaccelerationdrivenbytwocrossedAirybeams,OpticsLetters[OptLett]2011Mar1;Vol. 36 (5),648～50

6尹泽明，丁春利.精通MATLAB 6.北京：清华大学出版社，2002

7D.M.Greenberger.CommentonNonspreadingwavepackets·.Am.J.Phys.,1980,48(3): 256

The Similary between Schrodinger Equation and

Optical Near Axis Wave Equation,and Airy Beam

Dong MeifengSong XinxiangHan QiaoliZhu HuafengLiu Bing

(China University of Petroleum,Qingdao,Shandong266580)

Abstract:The Schrodinger equation is part of quantum physics in college physics teaching the basic equation,And how to get the non-diffracting beam in optical in recent years is an important subject in the field of optical research,In this paper,through the schrodinger equation and mathematical corresponding relationship between the optical paraxial wave equation,Got a kind of non-diffracting airy beam. In the university physics teaching through contact with the above research topic,Teaching results greatly improve the students′ scientific research quality and its various aspects ability.

Key words:university physics; Schrodinger equation; airy beam