正多边形顶角和各边带电在中心处场强的计算
2016-01-12杨培军
王 鹏 杨培军
(界首市界首中学 安徽 阜阳 236500)
正多边形顶角和各边带电在中心处场强的计算
王 鹏杨培军
(界首市界首中学安徽 阜阳236500)
摘 要:在正多边形每个顶角上各放置一个等量同种点电荷,则中心处合场强为零,对于这一结论本文给出了3种证明方法;并进而分析了正多边形每个边均匀带电等情况.
关键词:正五边形正多边形合场强点电荷对称
正多边形对称性强,匀称美观,是一种很常见的图形,如果让正多边形带上电荷,那么其中心处的电场强度是多少呢?本文分析了几种简单情况.
1正多边形各顶角均放置一等量同种点电荷
1.1问题的提出
【例1】在不少资料中,都有这样一道题:如图1(a)所示,A,B,C,D,E是半径为r的圆周上等间距的5个点,在这些点上各固定一个点电荷,除A点处的电荷量为-q外,其余各点处的电荷量均为+q,则圆心O处

图1
此题的关键在于证明一个结论:在正五边形每个顶角上各放置一个等量同种点电荷[如图1(b)],则正五边形中心处合场强为零.这个结论可以推广到正n边形的情况.本文给出了3种证明方法.
1.2结论的证明
1.2.1对称法
先证明边数为偶数的情况.此时正多边形具有中心对称性.以正六边形为例,如图2所示,很显然,各点电荷在中心O点产生的场强两两抵消,中心O点的合场强为零.

图2
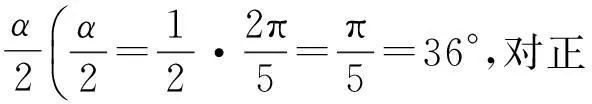

综上所述,无论正多边形的边数为偶数还是奇数,其中心处合场强均为零.

图3
1.2.2图像法
把表示场强的有向线段平移,使之成为一个首尾连接的正多边形.
以正五边形为例,在图4中,任选一个场强例如E3保持不动,平移E2,在平移时要注意在圆心O处E2和E3之间的夹角为72°(图4中α),而正五边形每一顶角为108°,恰好互补,因此将E2平移,使其起点为E3的终点,则E3的终点处角度恰好为108°,这说明E3的终点为正五边形的某一顶点.然后按顺时针顺序依次平移E1,E5,E4,即可得到一个首尾连接的正五边形,由此即可说明5个场强的矢量和为零.

图4


图5
1.2.3 平面向量法
我们直接证明正n边形的情况(图6).以正n边形中心为坐标原点,以En所在直线为x轴,垂线为y

α2=2α,E3与x轴夹角α3=3α,……,En与x轴夹角αn=nα.令场强大小为E,接下来我们写出每个场强在x,y轴上分向量合成的形式,在x,y轴上的单位矢量设为i,j.

图6
E1=iEcosα+jEsinα
E2=iEcos 2α+jEsin 2α
E3=iEcos 3α+jEsin 3α
……
En=iEcosnα+jEsinnα
E合=E1+E2+E3+…+En=
iE(cosα+cos 2α+…+cosnα)+
jE(sinα+sin 2α+…+sinnα)
下面我们来证明两个坐标均为零.这是很著名的三角函数题,利用积化和差等三角函数公式即可计算出结果,计算细节略去.
cosα+cos 2α+…+cosnα=

(1)
sinα+sin 2α+…+sinnα=

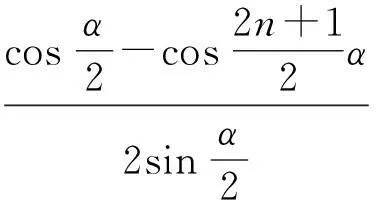
(2)
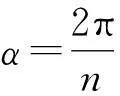

至此我们用了3种方法证明了结论,有了这个结论,接下来很容易就解决例1这道题了,解题过程从略.
2正多边形每个边都均匀带电
正多边形每个边都均匀带同种电荷,电荷的线密度为λ,且电荷固定,不能自由移动,则正多边形中心处合场强仍为零.我们用两种方法来证明.
2. 1将问题转化为正多边形每个顶角上带等量同种点电荷的情况
先来考虑某一个边在中心处产生的场强.如图7所示,由对称性很容易看出AB边在中心O点产生的场强沿AB边中垂线方向(具体方向要看电荷的种类),很显然在AB边中点处放置一适当同种点电荷q,可以在中心O点产生相同的场强,这样问题就转化成了图7(b)的情况(正多边形每个边不带电,每边中点均放置等量同种点电荷q),根据第一部分的结果,正多边形中心处合场强为零.至于电荷量q是多少,我们会在第二种方法中计算.
2. 2将问题转化为均匀带电圆环的情况
过中心O点作正多边形的内切圆[图8(a)],半径为R,让该圆均匀带电,电荷种类和线密度与正多边形均相同.设该内切圆与边AB的切点为C,如图8(b)所示,我们来证明边AB在中心O点产生的场强等于均匀带电圆弧A1B1在中心O点产生的场强[1].

图7

图8
在边AB上截取很短的一段DE,可视为点电荷,然后在OE上截取OF=OD,DE部分在中心O点产生的场强为
由此可见,线段DE与圆弧D1E1,弦D1E1在中心O点产生的场强相同,所以边AB在中心O点产生的场强与圆弧A1B1在中心O点产生的场强相同,整个正多边形在中心O点产生的场强与整个内切圆在中心O点产生的场强相同,等于零.
接下来我们继续计算.圆弧D1E1在中心O点产生的场强可以分解,由于对称性,沿水平方向的分量会互相抵消,我们来计算竖直方向的分量.
所以圆弧A1B1在中心O点产生的场强等于弦A1B1(图12中没有画出)在中心O点产生的场强.即

对于其他情况,例如正多边形每个顶点带不等量点电荷,也可得出相应结果.就不一一计算了.
3 结语
从以上讨论过程可以看出对称的重要性,对称不仅帮助我们认识现象的本质,而且可以使计算大为简化,使复杂的问题得以快速解决.对对称性的认识我们不能停留在感性认识上,更要注意认识其内部的对称性,而且还要能够充分发挥想象力,善于构造对称关系,以简化解题步骤[3].
参 考 文 献
1程稼夫.中学奥林匹克竞赛物理教程·电磁学篇.合肥:中国科学技术大学出版社,2004.11
2江志云,黄丽贞.对称性在高中物理教学中的初步研究.
收稿日期:(2015-01-16)
