GNSS接收机中载波相位周跳成因研究及性能分析

GNSS接收机中载波相位周跳成因研究及性能分析

马春江,唐小妹,陈华明,孙广富

(国防科学技术大学电子科学与工程学院卫星导航定位技术工程研究中心,长沙 410073)

摘要：通过对二阶载波跟踪环路进行建模,利用相平面理论分析周跳产生的原因,给出衡量环路周跳性能的两类指标:平均周跳时间和平均周跳概率,并得出两类指标的转换公式。具体分析环路噪声带宽、环路阶数、环路鉴别器类型对环路周跳性能的影响。仿真结果表明:较小环路噪声带宽、较低环路阶数、鉴别器鉴相范围较大的环路,具有更好的抑制周跳产生的能力,为降低环路周跳概率的环路参数优化设计提供参考。

关键词：载波相位;载波环;相平面图;平均周跳时间

doi:10.13442/j.gnss.1008-9268.2015.05.015

中图分类号：TN967.1

文献标志码：A

文章编号：1008-9268(2015)05-0081-05

收稿日期：2015-06-01

作者简介

Abstract:This paper is based on a second order carrier tracking loop model, it produce phase plane portrait theory to analyze the reason of cycle slip, it gives a measure of the performance of the two types of loop cycle slip indicators: the mean time of cycle slip and the average probability of cycle slip, and it gives two types of indexes conversion formula. Specific analysis was given to identify the impact of loop bandwidth, loop order and the type of loop discriminator on the properties of loop cycle slip. Simulation results illustrated that if the loop noise bandwidth is smaller, loop order is lower and loop discriminator range is larger, the ability to restrain cycle slip is better, and it provided a reference to reduce the loop cycle slip probability in the parameters design.

0引言

载波相位周跳是影响测量型接收机性能的关键性因素之一,周跳使载波相位的观测值出现偏差,从而不能准确解算整周模糊度,并严重影响接收机的精度[1]。在GPS的L1载波中,一周的相位周跳可以造成约 20 cm 的测距误差。

早在1963年,Viterbi 就对一阶模拟锁相环进行建模,基于福克·普朗克方程推导了一阶锁相环的平均周跳时间公式[2]。2008年,文献[3]通过蒙特卡洛仿真方法,建立了类似于一阶环的高阶锁相环平均周跳时间的解析表达式。数字环路的周跳性能研究相对较晚。1974年,文献[4]利用查普曼卡尔莫戈洛夫方程推导得出一阶数字锁相环平均周跳时间随载噪比变化规律。1996年,文献[5]在数字跟踪环路中运用该理论,用数值方法得出一阶、二阶、三阶环路平均周跳时间的理论结果,但没能导出解析表达式[5]。2009年,文献[6]通过实验仿真,对比分析锁相环、锁频环辅助锁相环和相位卡尔曼滤波在电离层闪烁影响下的周跳性能,但没有对其进行定量分析[6]。

虽然关于环路周跳的研究多、起步早,但由于分析方法复杂程度高,大多研究侧重分析简单环路的平均周跳时间,缺乏对实际环路周跳性能的定量分析。本文首先建立数学模型,分析周跳的成因;

然后给出几种常见的周跳性能评价指标;最后,分析环路鉴别器类型、环路噪声带宽和环路阶数对载波相位周跳的影响,并进行量化分析。

1周跳成因分析

在接收机进行连续的载波相位测量过程中,由于周跳的产生导致整周计数发生错误,但不足一周的部分仍然正常。下面给出分析周跳的数学模型,利用相平面方法对周跳的成因进行分析,并给出几种常用的周跳性能评价指标。

1.1　数学模型

接收机对信号进行跟踪主要是借助载波跟踪环路(简称载波环)和码跟踪环路(简称码环)来完成的,其中载波环通常有相位锁定环路(PLL)和频率锁定环路(FLL)两种形式。在测量型接收机的设计中,常采用二阶锁相环作为载波跟踪环路,为了便于对周跳问题进行建模,分析暂不考虑码环对载波的影响,得到的简化载波环模型如图1所示。

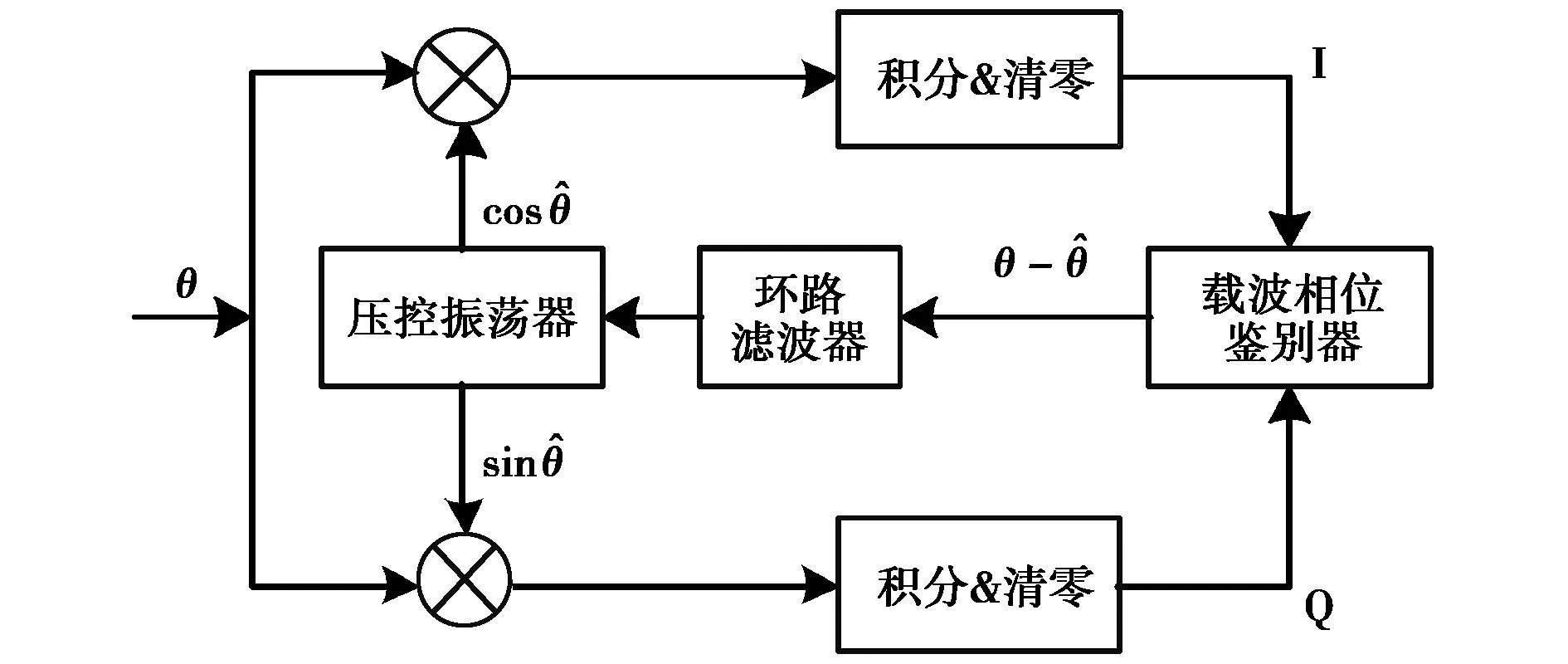
图1　载波环结构框图

联系人： 马春江 E-mail: mcj1174899621@163.com

如果环路输入固定频率信号,即输入信号的瞬时相位可以表示为

θ(t)=ωit+θ0,

(1)

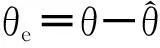
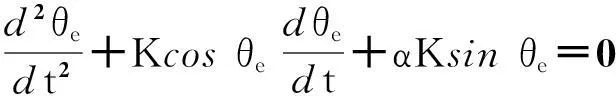
(2)

式中: K为环路增益系数; α为环路滤波器系数。

1.2　成因分析

相平面图(PhasePlanePortrait)可以用于研究二阶载波环路的瞬态非线性行为。根据式(2),将把时间作为自变量,相位误差θe和频率误差dθe/dt作为因变量,消去时间变量,就可得到一个用来表示相位误差和频率误差相互关系的二阶非线性微分方程。方程的解用dθe/dt和θe之间的关系式表示,可以画在以dθe/dt和θe为坐标的相平面上。其中,在相平面上的图形称为相平面轨迹,一组轨迹曲线可以组成相平面图,一条轨迹可以表示环路在趋于平衡状态时的瞬时行为。

如图2所示为二阶环路的相平面图,坐标横轴的上方dθe/dt>0,随着t的增加θe增大,因此相点移动的方向是由左向右;坐标横轴下方dθe/dt<0,随着t的增加θe减小,因此相点移动的方向是由右向左。

载波环路的相平面图本身就是呈周期性变化的,它的周期是变量θe的周期2π(纯锁相环),但对于dθe/dt是非周期的。图形是沿着θe无限重复的,图2中示出了两个周期。图中轨迹都是沿顺时针走向变化的,如图中箭头的方向。轨迹之间只在奇点处相交,而这些奇点可以是稳定或不稳定的。

稳定的奇点被称为平衡点,不稳定的奇点被称为鞍点,环路状态不能长久地停留在鞍点上,因为任何一个小扰动就使环路状态从鞍点进入一条活动轨迹,结束于鞍点的轨迹被称为分隔线[7]。图2中的分隔线用粗线表示。分隔线只是限于2π区间内,而且是指那些结束于鞍点且不返回无穷远处的轨迹。

如果一条轨迹位于两条分隔线之间,那么这条轨迹将结束于所在2π区间内的那个平衡点处。如果一条轨迹位于所有分隔线之外,那么环路就会发生一周或几周的滑步,然后到达平衡状态。一次周期滑步就表示相位误差达到了2π弧度。

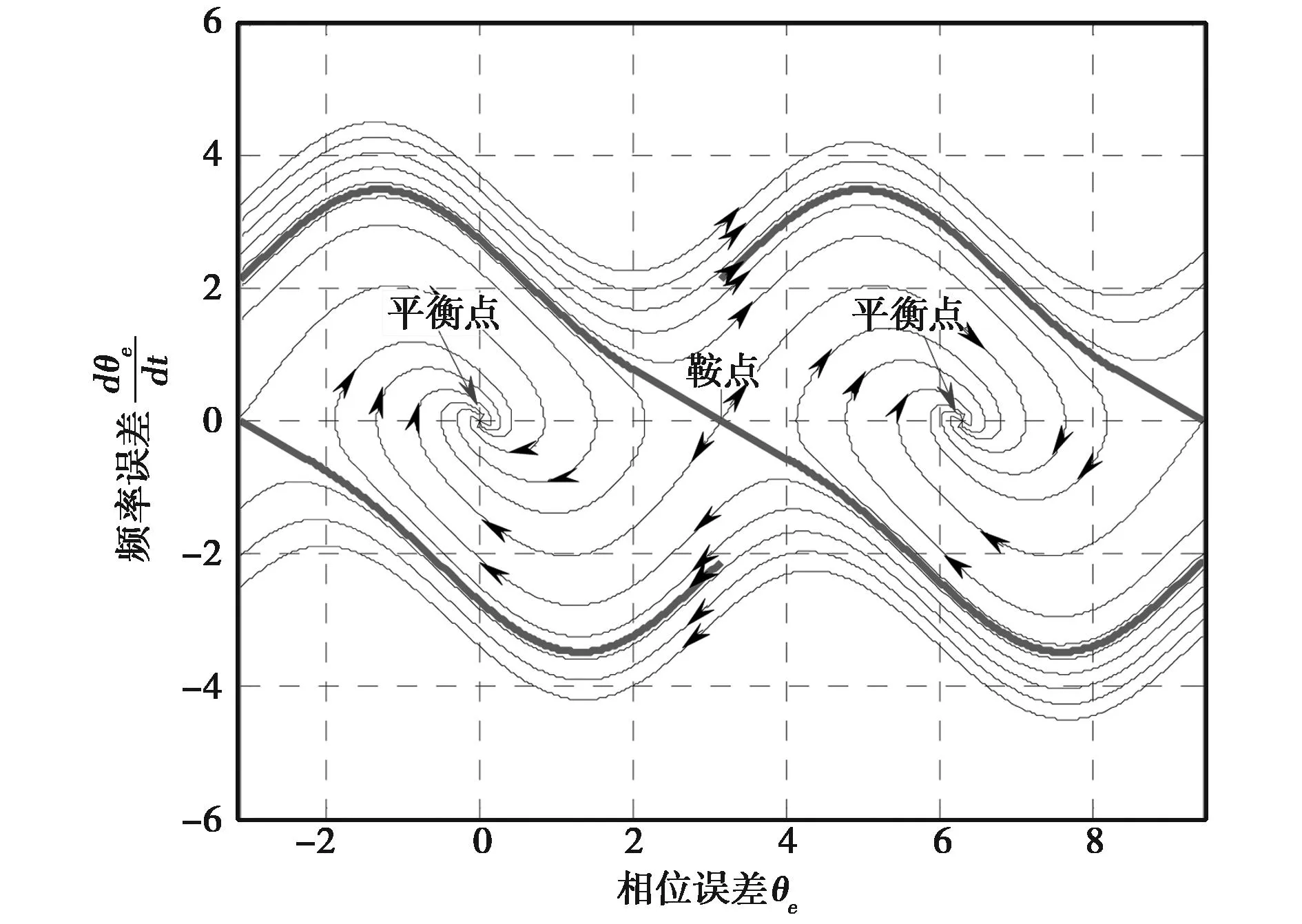
图2　一个简单二阶环路的相平面图

1.3　性能指标

在测量型接收机的数据后处理过程中,通常会有一些方法来对载波相位周跳进行探测和修复,但由于周跳的产生具有随机性,所以并没有很好的手段来对周跳的性能进行评估。通常的做法是,通过大量重复的实验,仿真环路一定时间内出现周跳的平均次数。下面给出两种常用的评价指标,它们在一定情况下可以相互转化,分别对应着不同的物理意义。

平均周跳概率即发生周跳的可能性。根据具体应用环境分为周跳速率、t秒不发生周跳的概率、t秒出现周跳的概率、t秒内出现K次周跳的概率。

文献[8]给出周跳速率是平均周跳时间的倒数,所以周跳速率为

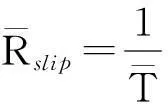
(3)

另外,Smith[9]证明载波相位跳变过程符合泊松分布,所以t秒内不周跳的概率为

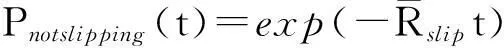
(4)

t秒出现周跳的概率为

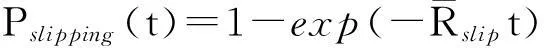
(5)

t秒出现K次周跳的概率为

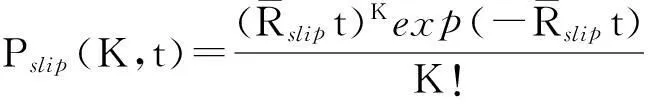
(6)

2环路设计对周跳性能的影响

载波相位周跳产生的根本原因在于正弦载波具有2π的模糊度,因此跟踪环路的设计对周跳的性能会产生很大影响。下面分别从环路鉴别器类型、环路噪声带宽和锁相环环路阶数三个方面进行分析。

2.1　环路鉴别器

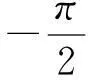
下面给出基于Costas鉴别器一阶锁相环路的平均周跳时间公式为[10]

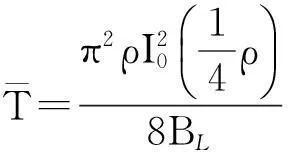
(7)

Q鉴别器一阶纯锁相环路的平均周跳时间公式为[11]

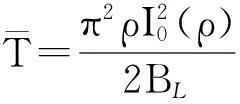
(8)

图3、图4分别给出不同环路鉴别器对应的平均周跳时间和1s内发生周跳概率的数值仿真结果。结果表明：纯锁相环的周跳性能要明显优于Costas锁相环。从鉴相的最大范围分析,纯锁相环对相位误差的容忍度为π,而在同等条件下,Costas环路则只能达到π/2。

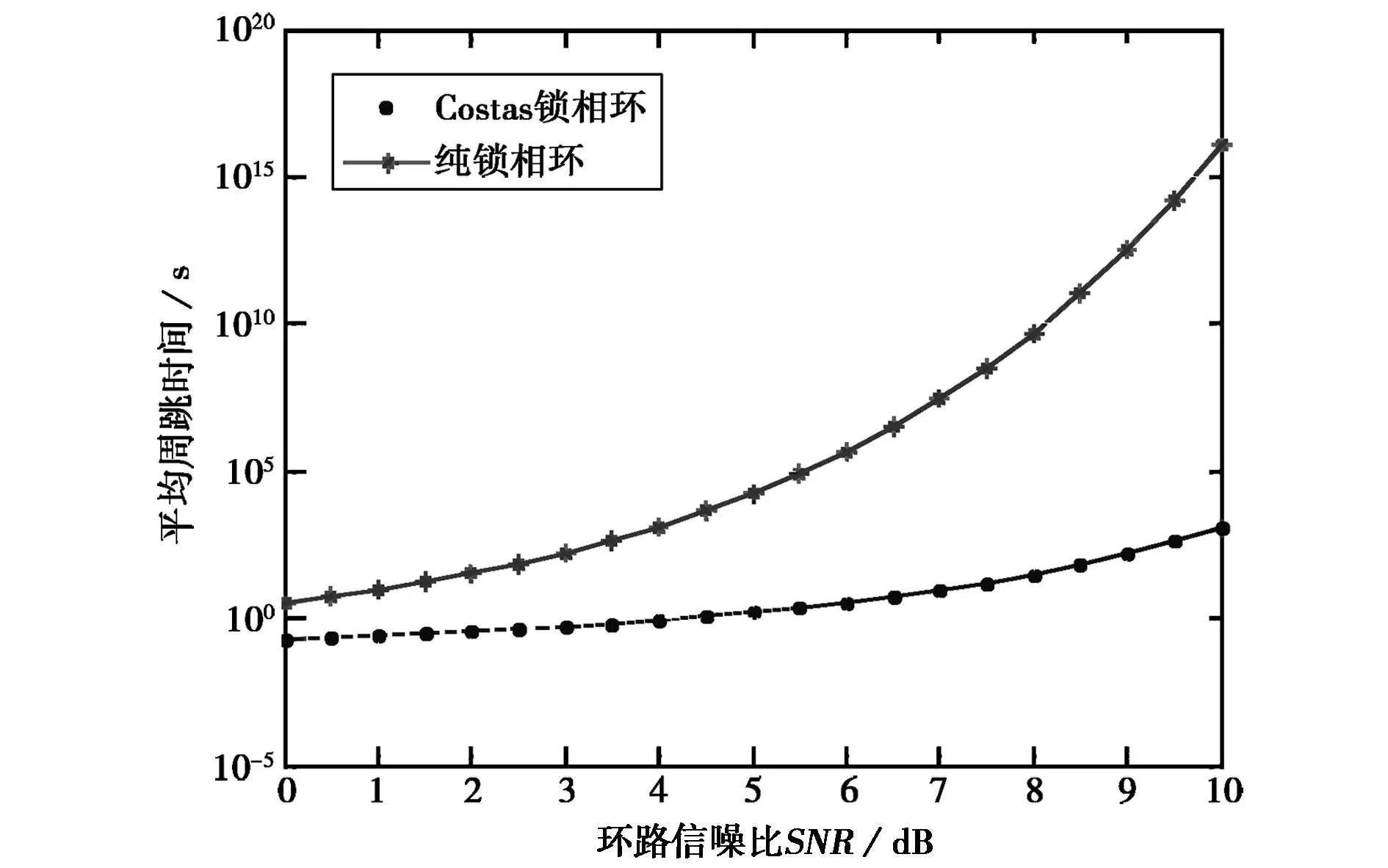
图3　鉴相器对平均周跳时间的影响

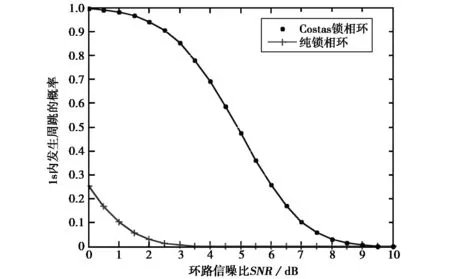
图4　鉴相器对周跳概率的影响

2.2　环路噪声带宽

环路噪声带宽直接影响环路输出的噪声大小,环路带宽越小,对输入信号中的白噪声的抑制作用越为明显。载波相位观测值中包含的噪声偏差影响载波相位的波动,噪声偏差越大则载波相位的波动越大,故越容易产生周跳。

根据式(7)和式(8),环路噪声带宽对周跳性能有着直接的影响。以二阶锁相环为例,分析在5 Hz、10 Hz和20 Hz三种不同环路噪声带宽条件下,环路平均周跳时间和1 s内出现周跳概率随输入信噪比的变化情况。

图5和图6的数值仿真结果表明:随着环路噪声带宽的增加,载波相位的平均周跳时间变短,周跳发生概率变大,环路的周跳性能下降。

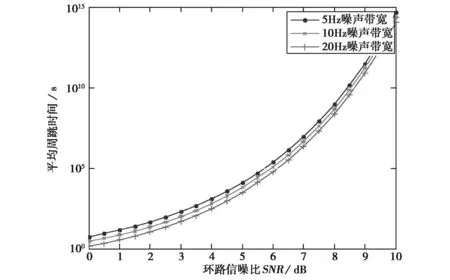
图5　环路噪声带宽对平均周跳时间的影响

2.3　环路阶数

环路阶数是指锁相环中环路滤波器的阶数,环路滤波器阶数直接影响环路对噪声的滤波效果。不同锁相环的阶数对应不同周跳性能,具体对应平均周跳时间为

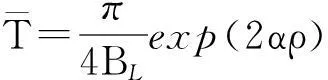
(9)

式中： ρ为输入信噪比,α=1对应为1阶锁相环,α=0.891对应为2阶锁相环,α=0.794对应为3阶锁相环。

图7和图8示出不同阶数环路滤波器下环路周跳性能的数值分析结果。结果表明：随着环路阶数的增加,环路的周跳性能变差。

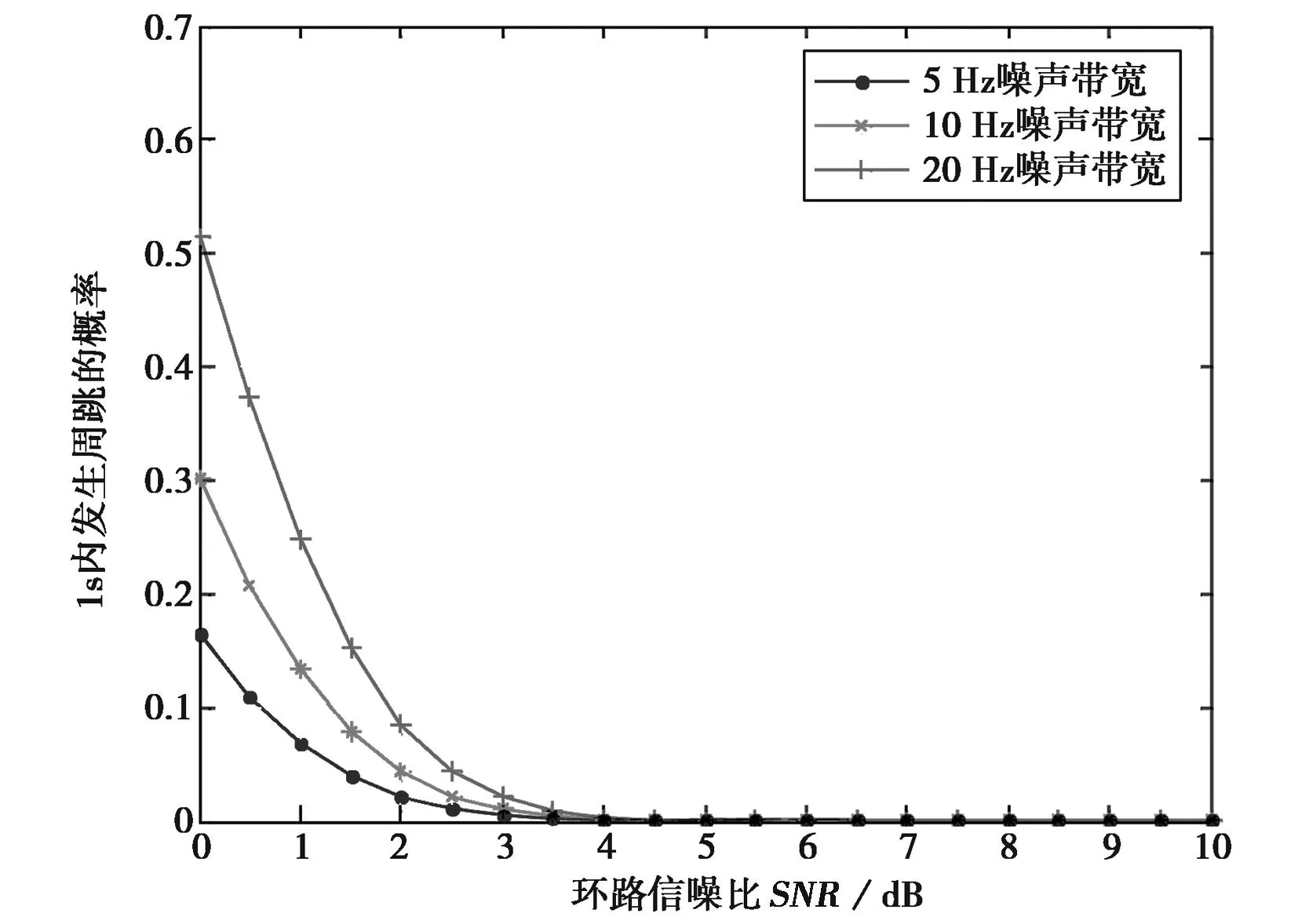
图6　环路噪声带宽对周跳概率的影响

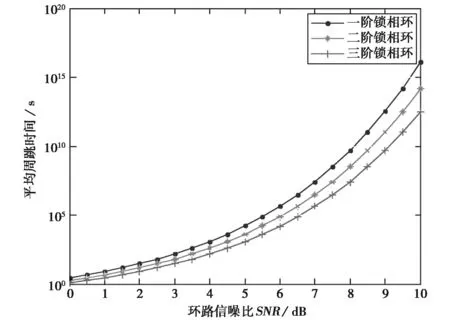
图7　环路阶数对平均周跳时间的影响

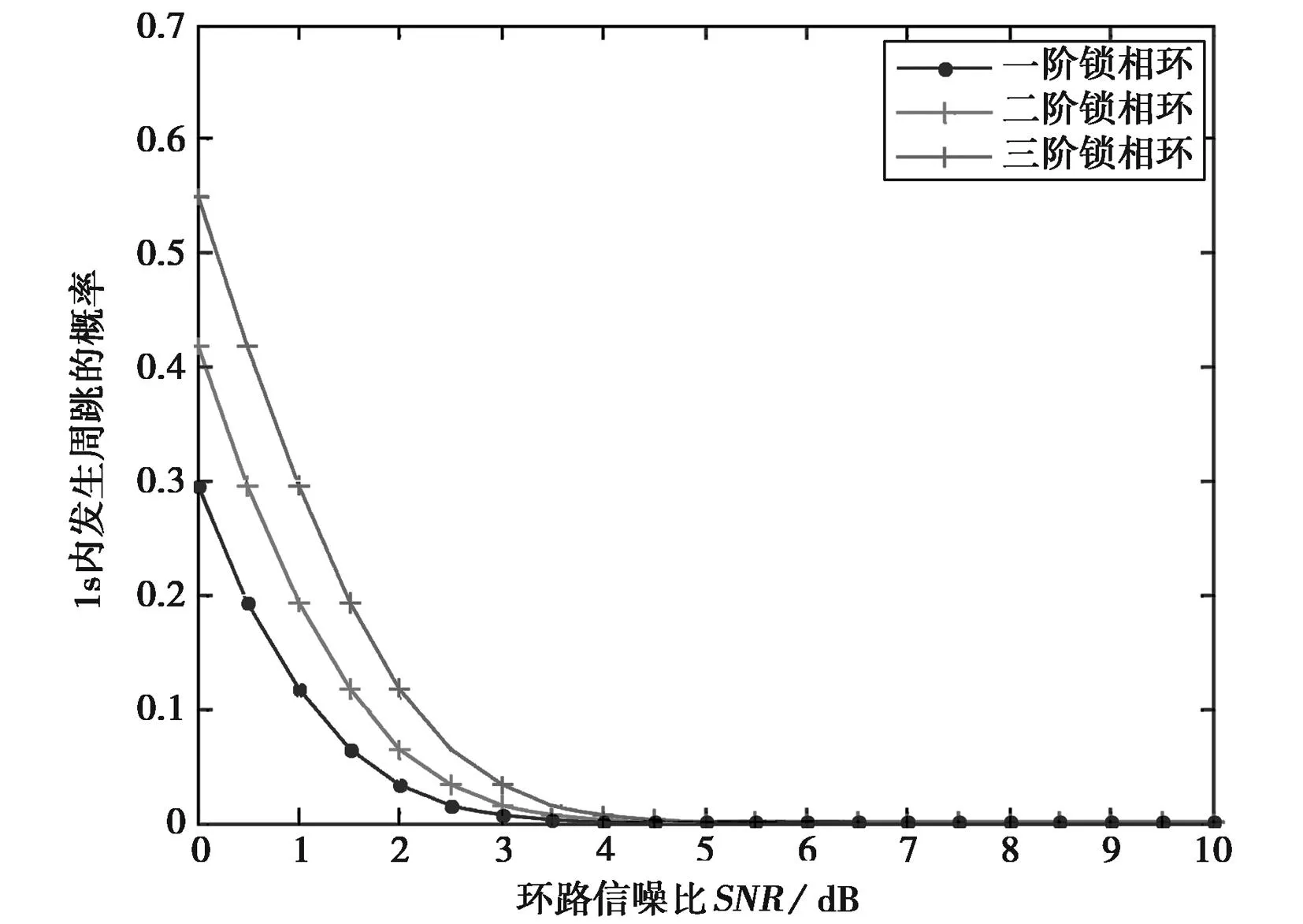
图8　环路阶数对周跳概率的影响

3结束语

文章首先对载波环路进行建模,根据环路的微分方程分析锁相环的相位误差变化规律。基于微分方程,画出二阶环路的相平面图,分析周跳产生的内在机理。通过对比分析,论证得出较小环路噪声带宽、较低环路阶数、鉴别器鉴相范围较大的环路,具有更好的抑制周跳产生的能力。文章得出的结论有利于理解载波相位周跳的产生,并对环路载波周跳的优化设计提供了参考。

参考文献

[1] 李征航,张小红.卫星导航定位新技术及高精度数据处理方法[M].武汉:武汉大学出版社,2009.

[2] VITERBI A J. Phase-locked loop dynamics in the presence of noise by Fokker-Planck techniques[C].//Proceeding of the IEEE, 2012, 51(12):1737-1753.

[3] HOLMES J K. The mean cycle slip time for first-, second-, and third-Order PLLs[J]. IEEE AC Paper, 2008, 5(1):1-8.

[4] WEINBERG A. Discrete time analyses of non-uniform sampling first-and second-order digital phase lock loops[J]. IEEE Transaction on Communications, 1974, 22(2):123-137.

[5] ZHUANG Weihua. Performance analysis of GPS carrier phase observable[J].IEEE Transactions on Aerospace and Electronics Systems, 1996, 31(2):754-767.

[6] ZHANG Lei. Tracking GPS signals under ionosphere scintillation conditions[C].//International Meeting of the Satellite Division of The Institute of Navigation, Savannah, 2009:22-25.

[7] GARDNER F M. Phaselock techniques[M].3 th ed. John Wiley & Sons, 2005.

[8] VITERBI A J. Principles of coherent communications [M]. McGraw-Hill, New York, 1966.

[9] SMITH B M. The phase lock loop with filter:Frequency of skipping cycles-theoretic considerations[J]. Proceeding of the IEEE, 1966, 51(12):817.

[10]HEGARTY C. Evaluation of the proposed signal structure for the new civil GPS signal at 1176.45 MHz: USA, WN99W0000034[P]. 1999-03-07.

[11]JULIEN O, ISSLER J L,RIES L. Investigation of Galileo E1 OS/SoL acquisition, tracking and data demodulation thresholds for civil aviation[C].//ION GNSS 2011:1264-1276.

马春江(1991-),男,湖南邵阳人,硕士生,主要研究方向为星基导航与定位技术。

唐小妹(1982-),女,江苏海安人,副研究员,主要研究方向为卫星导航信号处理、接收机设计。

陈华明(1969-),男,湖南宁乡人,副研究员,主要研究方向为卫星导航定位技术、接收机设计。

孙广富(1970-),男,黑龙江巴彦人,研究员、博士生导师,主要研究方向为卫星导航信号接收技术。

Causes Research and Performance Analysis of GNSS

Receiver Carrier Phase Cycle Slips

MA Chunjiang,TANG Xiaomei,CHEN Huaming,SUN Guangfu

(SatelliteNavigationandPositioningR&DCenter,SchoolofElectronic

ScienceandEngineering,NationalUniversityofDefense

Technology,Changsha410073,China)

Key words: Carrier phase; carrier loop; phase plane portrait; the mean time of cycle slip