BOC调制信号体制下多址干扰对伪码跟踪偏差影响分析

BOC调制信号体制下多址干扰对伪码跟踪偏差影响分析

周传宇,李井源,黄新明,黄仰博,孙广富

(国防科技大学电子科学与工程学院卫星导航定位技术工程研究中心,长沙 410073)

摘要：在远近问题严重的伪卫星或导航战功率区域增强典型场景下,用户机接收到的不同卫星信号功率不均衡,对于卫星信号监测的高精度伪码测距接收机,多址干扰成为必须考虑的误差因素之一,即使在导航现代化的新体制下影响也十分显著。本文在BOC调制信号体制下基于伪码跟踪非相干延迟锁定环路,对多址干扰影响伪码跟踪偏差的机理展开,从码跟踪环鉴别函数出发推导出伪码跟踪偏差的近似解析表达式,其后对BOC(1,1)调制信号体制下存在一路多址干扰时伪码跟踪偏差的影响进行分析和仿真验证,得出只有在伪码相位及载波相位差变化至特定位置时多址干扰影响明显,否则影响微弱;多址干扰影响与码跟踪相关器间隔变化较小,与多址干扰功率变化较大;在多址干扰功率高于期望信号功率20 dB时,跟踪偏差达到0.1个码片。

关键词：伪卫星;多址干扰;二进制偏移载波调制;非相干延迟锁定环;跟踪偏差

doi:10.13442/j.gnss.1008-9268.2015.05.011

中图分类号：P228.4

文献标志码：A

文章编号：1008-9268(2015)05-0058-07

收稿日期：2015-07-17

作者简介

Abstract:In the scenario of pseudo satellites which facing a serious near-far problem or power region enhancement in navigation warfare, user receive different signals with various power levels, as a result, the impact of multiple access interference for high precision PN code ranging signal detection receiver is one of the major factors that must be considered,even for the new generation navigation system. In this paper the principle of multiple access interference effects on the noncoherent delay locked loop PN code tracking deviation is analyzed, based on the binary offset carrier (BOC) modulated signal system. An approximate analytical expression of the pseudo code tracking deviation is derived from the phase detector function, then the effect of single multiple access interference on the pseudo code tracking deviation and simulation analysis is carried out for BOC(1,1) modulated signal, concluding that the effect of multiple access interference is obvious only when the carrier phase difference and the phase difference of the PN code is changed to a specific position, and is a little influenced by the correlator spacing, while much influenced by multiple access interference power. The pseudo code tracking deviation reaches 0.1 chips when the multiple access interference power is 20 dB higher than the expected signal power.

0引言

卫星导航系统的高速发展对导航性能提出了更高的要求,伪距跟踪偏差受到多种因素的影响,由于扩频伪码互相关峰值相对自相关峰值较小,传统观点认为多址干扰引起的伪码跟踪偏差可以忽略不计,然而对于某些特殊的场景,如导航战中采用区域增强技术或者卫星信号接收存在严重遮挡时,多址信号功率远高于期望信号功率,多址干扰成为必须考虑的误差因素之一;在存在伪卫星条件下卫星发射功率远近问题严重,其引起的伪码测距误差不可忽略[1]。现有文献将多址干扰引起的伪码测距误差近似看成高斯白噪声造成的影响进行分析[2],文献[3]对GPS系统中多址干扰引起的伪距测量误差做了定性分析,但未给出严格的解析表达式,且未分析多址干扰在何种情况下成为不可忽略的误差因素。文献[4]给出了存在多址干扰时伪码跟踪环路最大误差的解析表达式,指出了影响最大误差的关键因素,然而并未深入探讨用户功率差及码跟踪相关器间隔等参数的影响机理。文献[5] 针对卫星导航系统中联合检测和干扰消除的多用户检测技术进行了对比，并针对准同步传输体制研究了其在多址干扰抑制方面的能力，但并未涉及到BOC调制技术。在导航现代化新体制大趋势下,对于BOC调制信号体制下多址干扰的研究非常有意义也十分迫切,本文以两路BOC(1,1)调制信号为例,从互相关函数对于自相关函数的畸变出发,给出了存在一路多址干扰条件下的伪码跟踪偏差的解析表达式,其后对多址信号中对多址误差影响较大的关键因素进行仿真分析,最后得出BOC调制信号体制下存在一路多址干扰时对伪码跟踪偏差的影响规律。

1存在多址干扰时伪码跟踪环路理论推导与分析

1.1　BOC调制信号伪码跟踪环路建模

联系人： 周传宇 E-mail: zhouchuanyu@126.com

导航用户接收机一般采用延迟锁定跟踪环进行伪码测距,本文分析模型为非相干延迟锁定跟踪环结构,如图1所示。

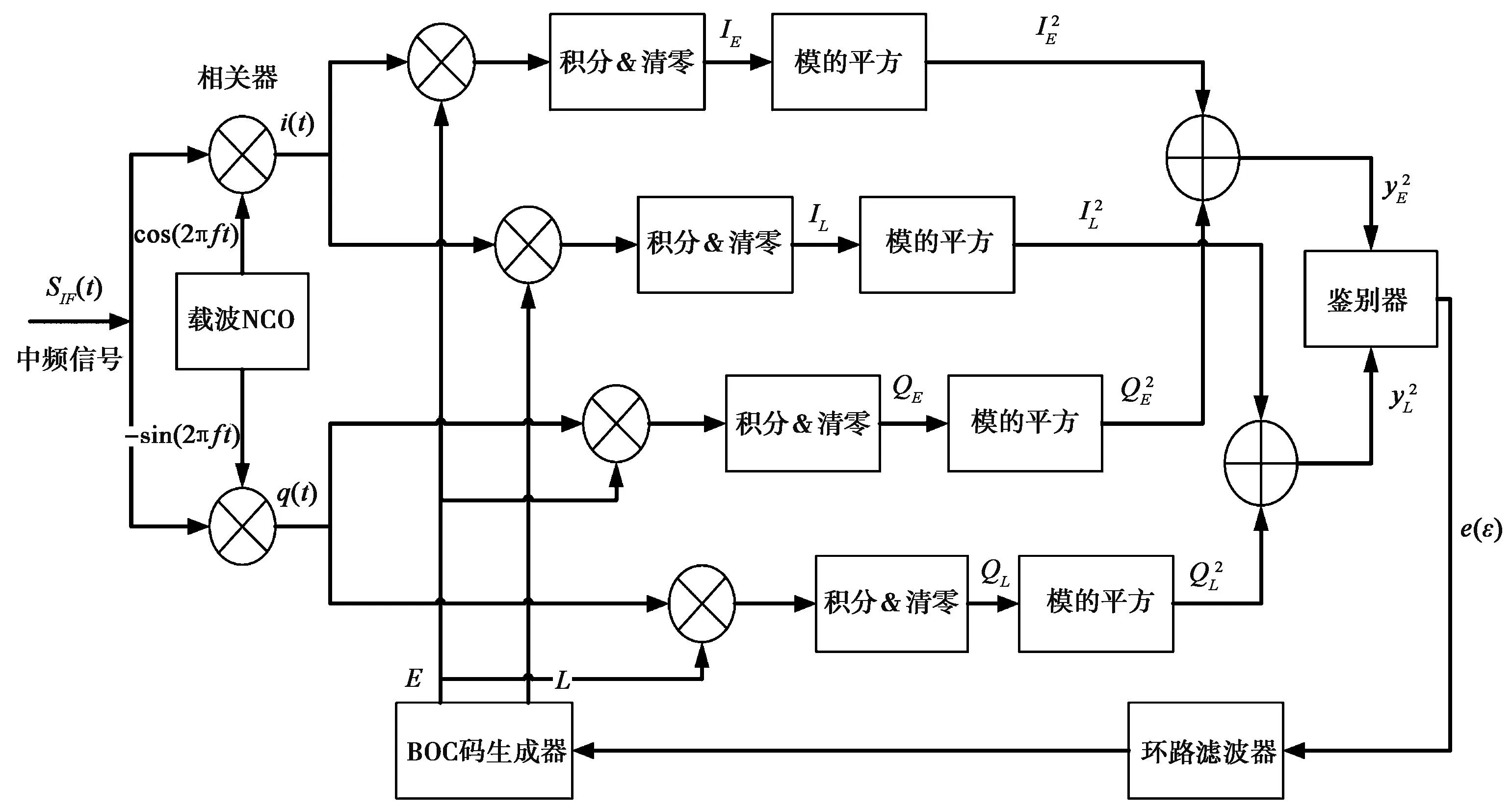
图1　非相干延迟锁定跟踪环原理示意图

假设接收机接收到K路BOC调制扩频信号,其表达式为

exp[j(ωct+θi]+nR(t)，

(1)

式中: pi为扩频信号的平均功率; di(t)为调制数据; ai(t)为副载波调制的扩频码; τi表示信号传输时延; θi为载波相位初相; nR(t)为带限高斯白噪声。使用di和ai替代di(t)和ai(t)。本文以两路用户为例,其中第一路用户为期望用户,第二路为多址干扰用户,考虑到高斯白噪声对于伪码跟踪的系统误差影响较小,忽略式中的高斯白噪声项。如图1所示,采用非相干延迟锁定环路进行伪码跟踪以消除载波跟踪误差和符号位的影响[6],归一化后的早迟鉴别器的输出表达为

(2)

使用符号ε表示期望信号时延估计偏差,τ为干扰信号的相对时延,Δ为码相关器间隔,θ为载波相对相位差,R1i(·)为BOC调制扩频码互相关函数,式中鉴别器输入量可表示为[5]

(3)

1.2　BOC调制信号体制下的伪码相关特性分析

自相关函数是GNSS信号的重要特性之一,它直接影响着信号的质量和用户机的接收[7]。设BPSK调制基带信号表达式为

(4)

式中:bi代表调制数据码后的伪码;扩频符号μTc(t)代表宽度为Tc的矩形脉冲信号;ts代表副载波信号周期的一半;n为调制系数, BOC调制基带信号是在BPSK调制基带信号使用副载波再调制而成,表示为

(5)

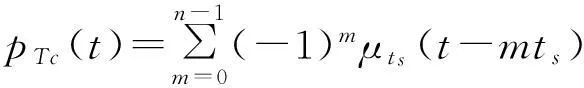
(6)

式中:Rb(i)为伪码序列的自相关函数;Rμ(τ)为扩频符号自相关函数;Rp(τ)为码片波形自相关函数,可得BOC调制信号平均自相关函数为码片波形自相关函数对BPSK调制信号平均自相关函数的加权累加。

如图2所示为BOC调制信号副载波对自相关函数的加权影响图,其中带星虚线代表单个码片内码片波形的自相关函数,为式(6)乘号左边部分代表的BPSK调制非周期伪码的平均自相关函数表达式,带圈实线代表对这些自相关函数的叠加部分,即为乘号右边码片波形引起的加权函数。

根据公式(6)得到如图3所示的BOC调制信号平均自相关函数图,τ为整数码片时,其自相关的取值在1,63/1023,-1/1023,-65/1023,65/1023,33/1023,1/1023,-31/1023,-63/1023,-511/1023十个峰值之间,前四个峰值为BPSK调制信号的相关峰值,后六个相关峰值为副载波对原相关峰的变换而得来,可以验证BOC调制信号的平均自相关函数是在BPSK调制信号平均自相关函数上进行相应的变换得到的。

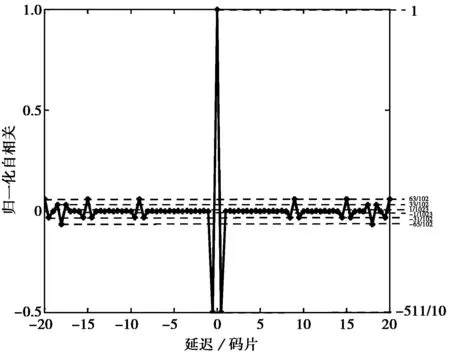
图3　BOC调制信号平均自相关函数

由于副载波调制并没有破坏BPSK调制信号中互相关与自相关函数之间的联系,同理可得如图4所示的某一不相同BOC调制信号之间的互相关函数图。

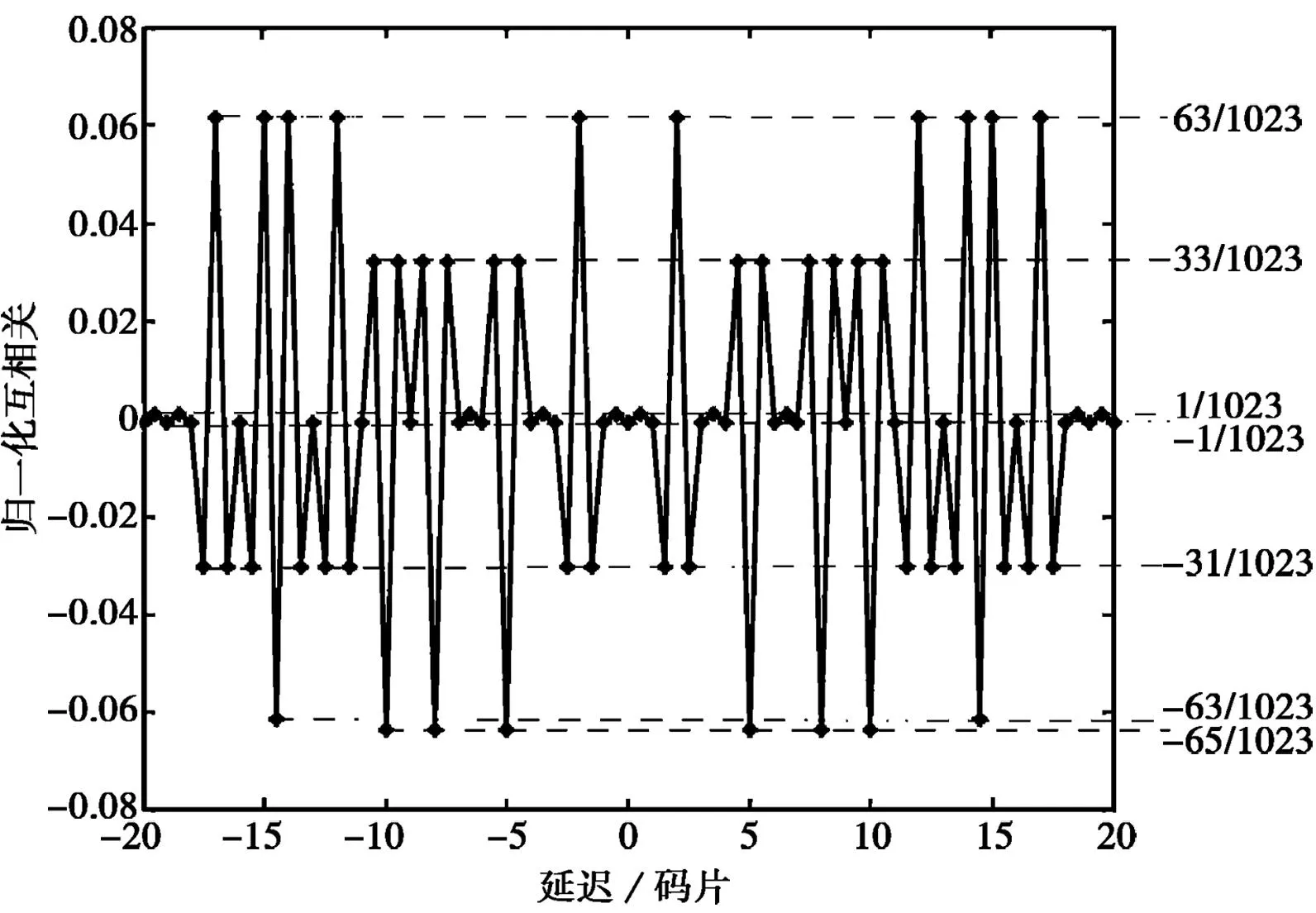
图4　BOC调制信号互相关函数

1.3　BOC调制信号体制下伪码跟踪偏差分析

伪码跟踪环路零值偏差为使鉴别器输出为零时的时延估计偏差值[8],即满足:

(7)

将式(3)代入式(7)可得:

e(ε)=g1(ε)g2(ε).

(8)

式中:

(9)

(10)

本文仅考虑码跟踪环锁定在自相关主峰的情况进行研究,即码环鉴别器正常工作在线性区域,不考虑BOC调制自相关函数的多峰特性造成的错锁现象[7]。在此情况下因式g1(ε)不为零,因此式(7)可以等效转化为求解等式

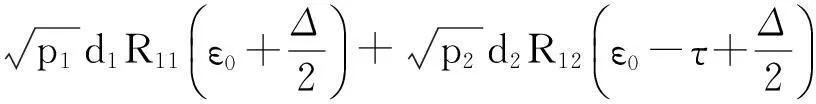
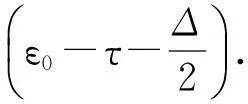
(11)

设R11(·)在自变量为0、Tc/2处取值分别为1、m,Tc为扩频码码片宽度,R12(·)在自变量为kTc/2处取值为uk,k为整数。R11(·)和R12(·)可以表示为关于自变量的分段函数

(12)

R12(t)= uk+2(uk+1-uk)t/Tc,

t∈[kTc/2,(k+1)Tc/2].

(13)

将式(12)和式(13)代入等式(11)中,当τ∈[τ1,k,τ2,k]时,相对延迟造成互相关峰值处于分段函数两段内,此时偏差跟τ有关,当τ∈[τ2,k,τ1,k-1]时互相关峰值处于分段函数同一段内时,偏差跟τ无关,综合为

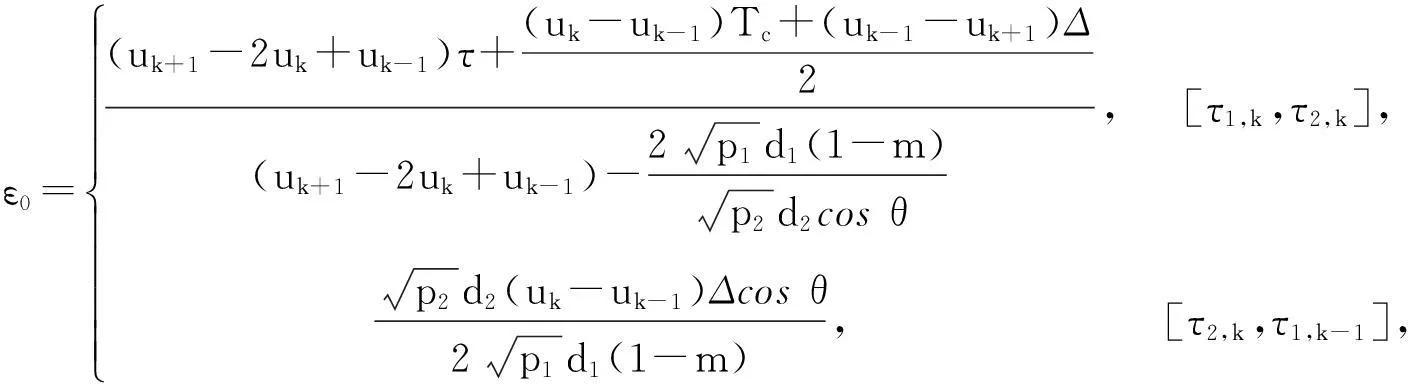
(14)

式中:

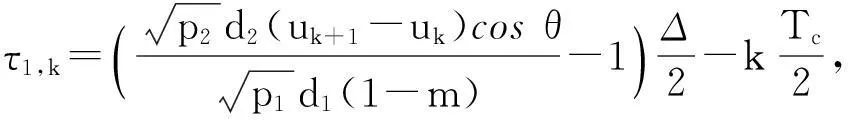
(15)

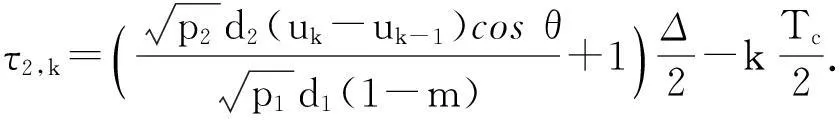
(16)

由式(14)可得,多址干扰引起伪码跟踪偏差主要取决于以下四项: 1) 多址干扰相对期望用户的载波相位差; 2) 多址干扰用户相对期望用户时延,相对时延导致载波相位差和伪码相位差的变化,其中伪码相位差造成与自相关主峰相对应的互相关值存在差异,伪码跟踪偏差与其值联系密切; 3) 延迟锁定环的相关器间隔,伪码跟踪偏差随其值减小而减小; 4) 多址干扰用户与期望用户功率之比,其值越大,伪码跟踪偏差随之增大;

2BOC调制信号体制下伪码跟踪偏差仿真验证

与理论分析模型相对应,仿真验证平台采用两路信号,其中第一路为期望用户,采用1号卫星的扩频码,第二路为多址干扰用户,采用2号卫星的扩频码。由于扩频码之间的互相关特性表达复杂,采用指定的卫星扩频码在一定的伪码相位差范围内进行分析,在可以简化分析同时,其具有代表性的结论同样适用于其它位置和其它卫星,仿真验证平台具体参数如表1所示。

2.1　载波相位差对伪码跟踪偏差的影响

为方便分析载波相位差对偏差的影响,给出其它重要变量的取值,在如表2所示的仿真环境中进行分析。

如图5所示为载波相位差对伪码跟踪偏差影响曲线图,根据公式(14)可得图中带圈实线为理论上伪码跟踪偏差曲线,载波相位差相对于其它变量

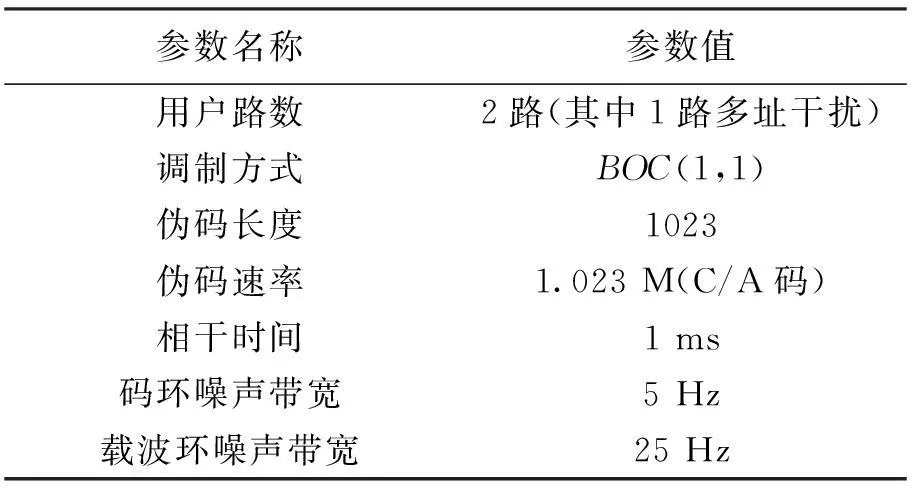
表1　仿真验证平台基本参数表

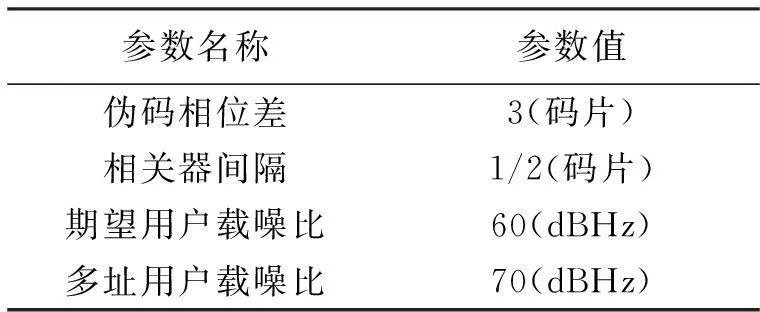
表2　载波相位差影响分析其它仿真参数表

而言属于快变量,跟踪偏差函数随着载波相位差的余弦函数呈近周期性变化。在一个变化周期内,在0和2π处分别达到伪码跟踪偏差的极点值,而当载波相位差靠近π/2或3π/2时,伪码跟踪偏差接近为0.图中带叉虚线为按照如上仿真平台参数仿真得到的载波跟踪偏差值,其值基本同理论曲线吻合。可见快变化的载波相位差对伪码跟踪偏差影响较大,为方便研究接下来均建立在载波相位差为0时进行展开分析。

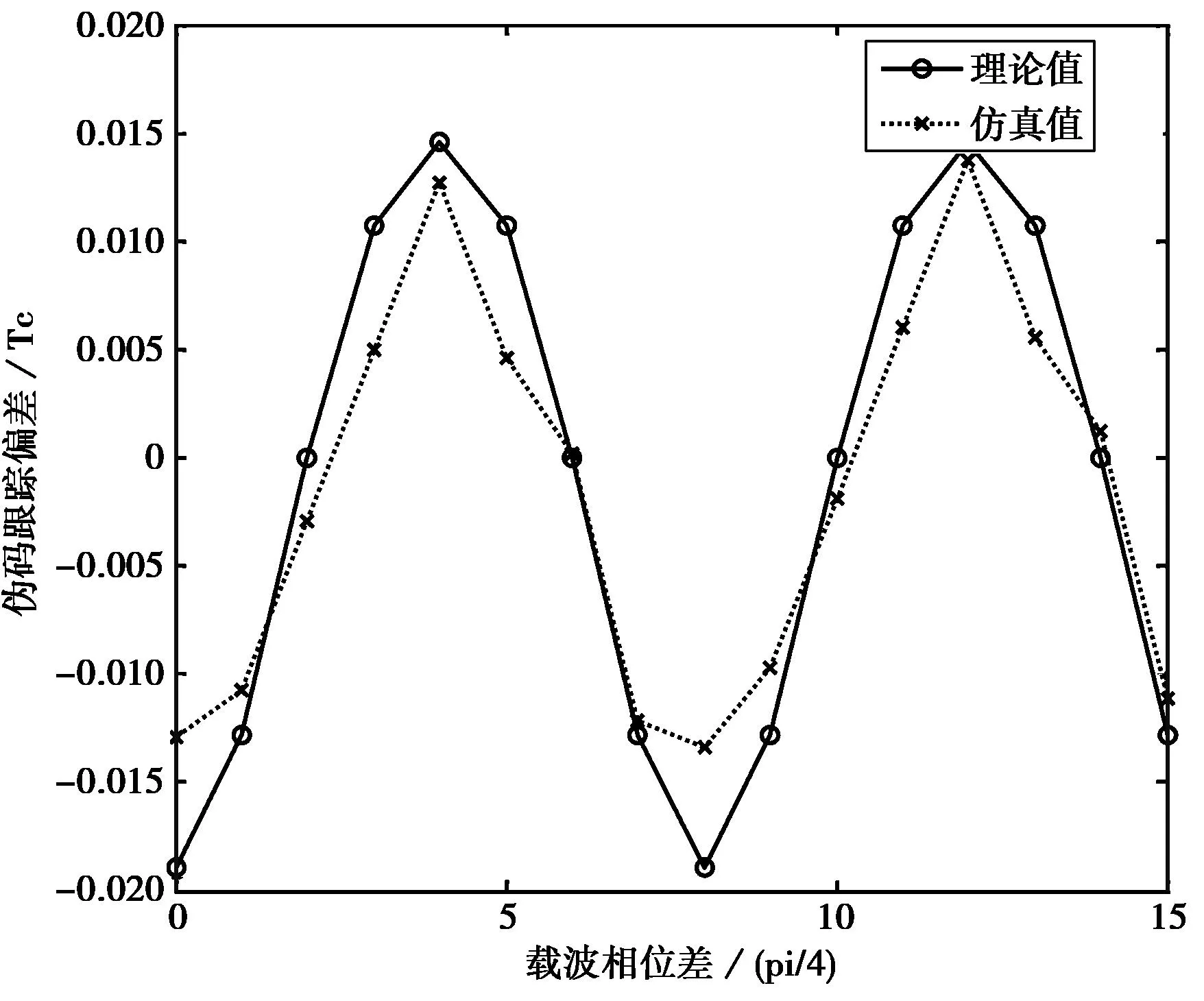
图5　载波相位差对伪码跟踪偏差影响曲线

2.2　伪码相位差对伪码跟踪偏差的影响

采用如表3所示为其它重要变量给定特定取值的仿真环境中进行分析。

表3　伪码相位差影响分析时其它仿真参数

考虑相对时延对于伪码跟踪偏差的影响可以归结于载波相位差和伪码相位差对伪码跟踪偏差的影响,载波相位差对于伪码跟踪偏差的快变化影响已经在上一节中分析,本节主要分析伪码相位差对于伪码跟踪偏差的影响。由于不同用户之间的互相关函数存在差异,因此很难解析地表达,图6为指定卫星条件下伪码相位差对伪码跟踪偏差曲线图,由于伪码相位差引起跟踪偏差值公式(14)中的下面一项表达式取值范围较小,在图中暂不做考虑。对比于图4中表示的BOC调制信号互相关函数,伪码相位差导致互相关主峰与副峰与自相关峰或副峰基本对齐时,多址干扰引起伪码跟踪偏差较大,而在其它处多址干扰引起的伪码跟踪误差相对较小,可以忽略。图中带叉虚线为仿真值与带圈实线表示的理论值基本吻合,但在自相关主峰对齐互相关副峰值附近处时存在较大的误差。

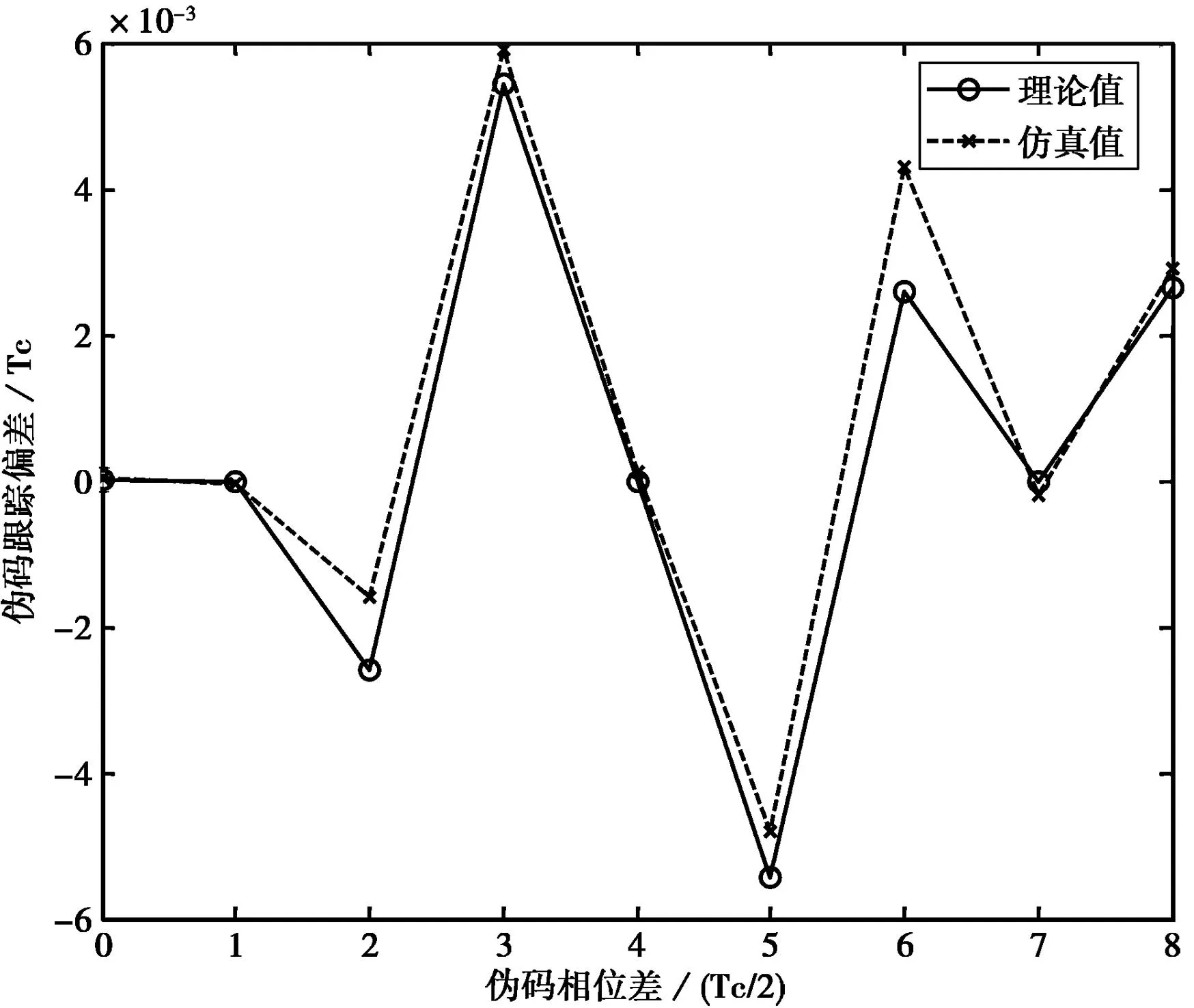
图6　伪码相位差对伪码跟踪偏差影响曲线

2.3　相关器间隔对伪码跟踪偏差的影响

为分析相关器间隔对伪码跟踪偏差的影响,给定其它重要变量取值如表4所示。

图7所示为码跟踪相关器间隔对伪码跟踪偏差的影响曲线图,从图中带圈实线可以看出随着相关器间隔的增长,伪码跟踪偏差呈线性增加,图中带叉虚线为仿真曲线基本与理论曲线吻合。对比于不存在多址干扰信号时相关器间隔的影响,可得不同于载波相位差和伪码相位差的快速剧烈变化,相关器间隔的影响主要归结于对于伪码跟踪环路的本身影响,对于多址干扰产生的跟踪偏差的影响是微弱的。

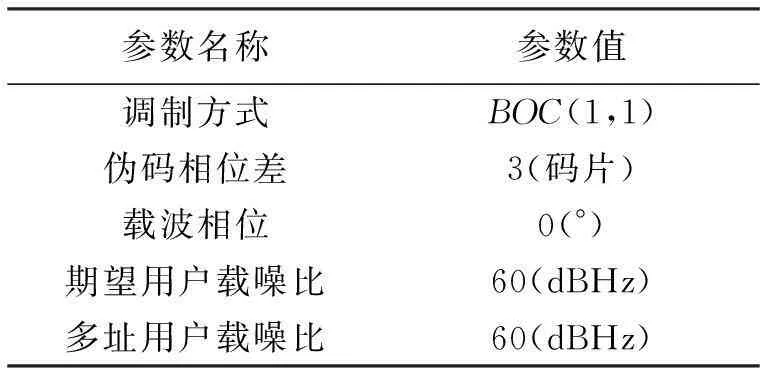
表4　相关器间隔影响分析时其它仿真参数

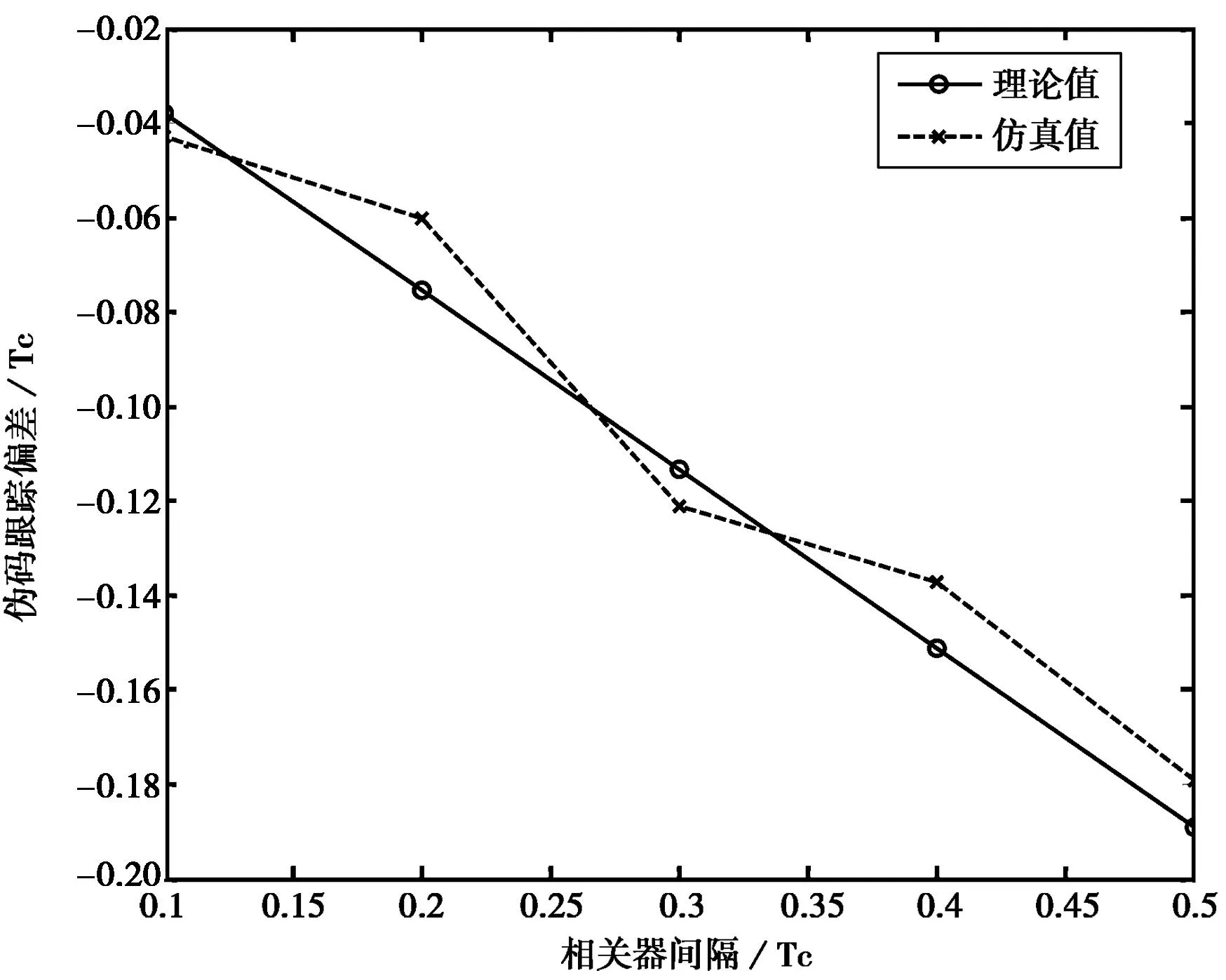
图7　相关器间隔对伪码跟踪偏差影响曲线

2.4　用户功率差对伪码跟踪偏差的影响

为分析用户功率差对伪码跟踪偏差的影响,如表5所示,在其它重要变量给定特定取值的仿真环境中进行分析。

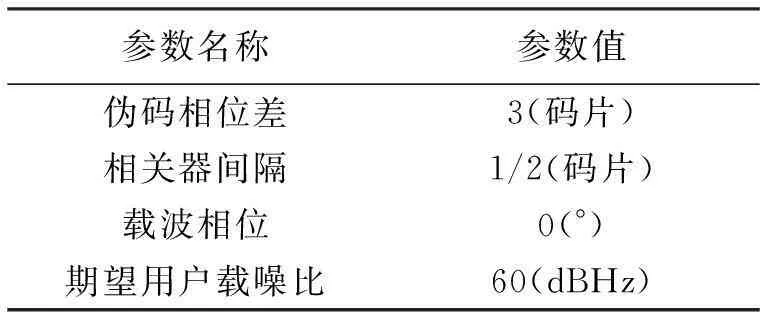
表5　用户功率差影响分析时其它仿真参数

在伪卫星存在的典型场景下,多址干扰信号特点主要体现在用户功率不平衡,如图8所示,当期望用户载噪比为60 dBHz时,伪码跟踪偏差随多址用户载噪比变化曲线图,从图中带圈实线表示的理论曲线的可以得出,随着多址干扰信号的载噪比增加,伪码跟踪偏差随之增大,带叉虚线为仿真曲线,在多址干扰信号载噪比较低时同理论曲线吻合得较好,载噪比较高时存在一定的误差,但并不影响基本的变化趋势,当多址用户较期望用户载噪比高出20 dB时,伪码跟踪偏差可达到0.1个码片。

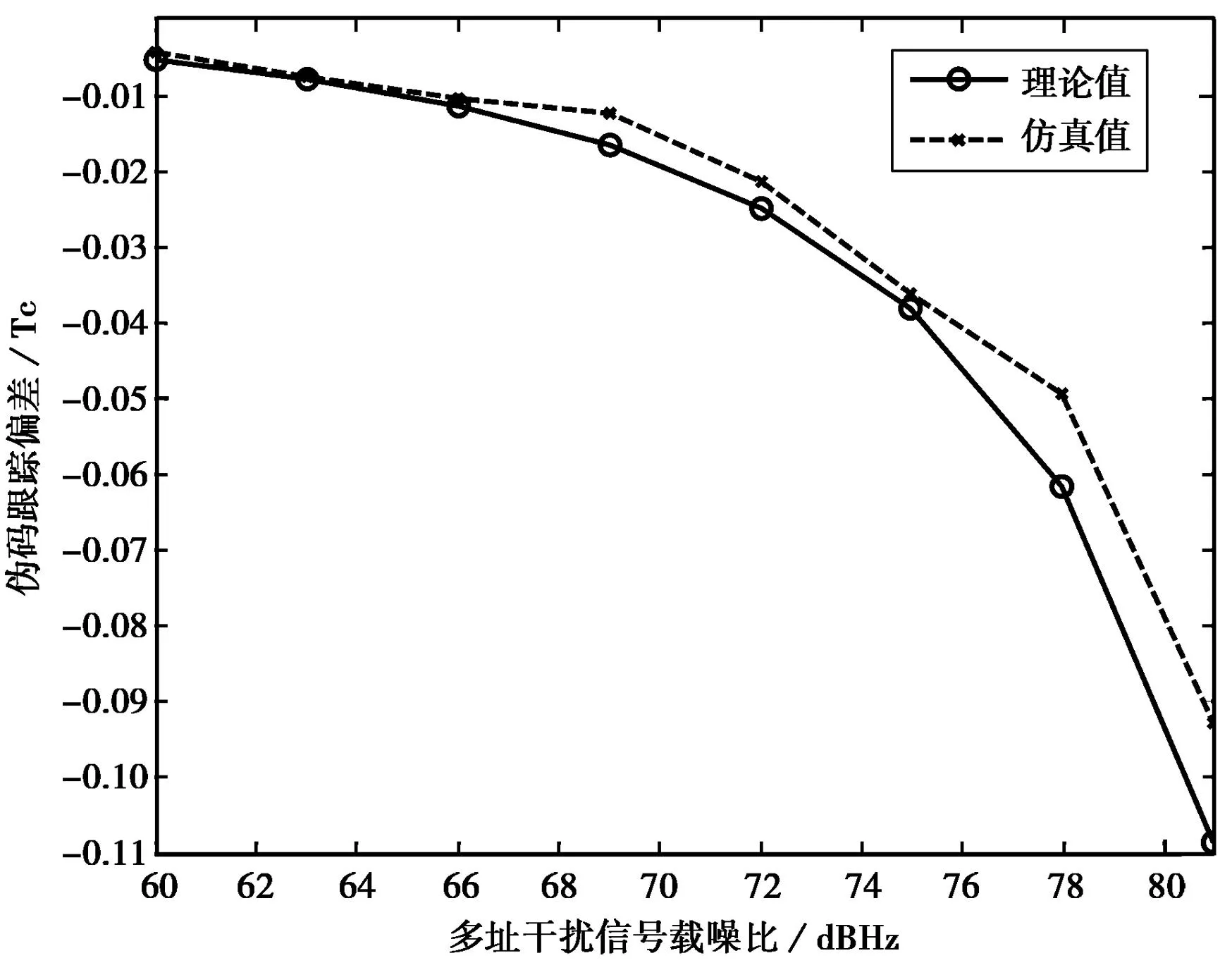
图8　用户功率差对伪码跟踪偏差的影响曲线

3结束语

本文研究了BOC调制信号体制下多址干扰对接收机非相干延迟锁定环伪码跟踪偏差的影响,得出了以下的结论:多址干扰载波相位差和伪码相位差对于伪码跟踪偏差的影响属于有规律的快变化,仅当在某些特定的位置造成较大的影响;窄相关有助于降低伪码跟踪偏差,但是并不能有效减轻多址干扰影响;多址干扰功率大小对伪码跟踪偏差影响显著,当多址用户功率高于期望用户功率20 dB时,码跟踪环跟踪偏差可达0.1个码片。研究结果对于分析多址干扰和抑制算法提供理论基础,可为进一步进行多址干扰抑制的提供支持,为新体制下导航战功率区域增强及伪卫星场景下的接收机设计提供参考。

参考文献

[1]李井源.卫星导航系统多址干扰影响分析及其抑制技术研究[D] .长沙:国防科技大学,2014.

[2]HONG S,YOON S,LEE H,etal. Performance analysis of noncoherent delay-locked loop in multiple access interference[J]. IEICE Trans Comm, 1995,78(7): 935-941.

[3]RVN D J.Spread-spectrum code and carrier synchronization error caused by multipath and interference [J].IEEE Trans on AES,1993,29(4):1359-1365.

[4]李星,王飞雪,欧钢,等.卫星导航系统中多址干扰引起的伪码跟踪误差分析[J].信号处理，2008,24(5):885-888

[5]楚恒林,范建军,张天桥.多址干扰抑制技术在卫星导航系统的应用研究[J].无线电工程 2015(7):50-53.

[6]PARKINSON B,SPILKER J. Global positioning system:Theory and applications[M].AIAA,1996.

[7]谢钢.全球导航卫星系统原理—GPS、格洛纳斯和伽利略系统[M].北京:电子工业出版社,2013.

[8]刘瀛祥.现代化导航信号高精度建模与接收技术研究[D].长沙:国防科技大学,2014.

周传宇(1992-),男,硕士生,主要从事卫星导航信号处理等方面的研究。

李井源(1982-),男,博士、讲师,主要从事卫星导航系统体制设计、接收机信号处理、站间时间频率传递等方面的研究。

黄新明(1988-),男,博士,主要从事卫星导航系统信号体制设计及信号处理算法等方面的研究。

黄仰博(1980-),男,博士、讲师,主要从事卫星导航定位、卫星导航信号处理、卫星导航接收机设计等方面的研究。

孙广富(1970-),男,博士生导师,研究员,主要从事卫星导航方面的研究。

Study on PN Code Tracking Deviation Caused by Multi-user

Interference in BOC Modulated Signal System

ZHOU Chuanyu,LI Jingyuan,HUANG Xinming,HUANG Yangbo,SUN Guangfu

(SatelliteNavigationPositioningR&DCenter,SchoolofElectronicScienceandEngineering,

NationalUniversityofDefenseandTechnology,Changsha410073,China)

Key words: Pseudo satellite; multiple access interference; BOC; noncoherent delay lock loop; tracking deviation