通道非理想对BPSK-Like算法跟踪性能的影响
2016-01-12张岩,刘瀛翔,唐小妹等
通道非理想对BPSK-Like算法跟踪性能的影响
张岩,刘瀛翔,唐小妹,孙广富
(国防科学技术大学电子科学与工程学院卫星导航定位技术工程研究中心,长沙 410073)
摘要:随着对定位精度要求的逐渐提升,通道特性对跟踪结果的影响已不能忽略。针对通道非理想条件下BPSK-Like算法的跟踪性能展开研究,对BPSK-Like算法的处理过程进行建模,在此基础上推导了几种特殊通道影响下的码跟踪性能并进行了仿真验证。通道的非理想特性并不一定会对码跟踪精度产生影响,一般而言,相频响应非理想会对码跟踪偏差产生影响,但对码跟踪精度的影响有限;单纯的幅频响应非理想则不会影响码跟踪性能。
关键词:BOC信号;边带跟踪算法;通道非理想;码跟踪性能
doi:10.13442/j.gnss.1008-9268.2015.05.012
中图分类号:TN967.1
文献标志码:A
文章编号:1008-9268(2015)05-0065-06
收稿日期:2015-05-22
作者简介
Abstract:With a higher requirement on tracking performance, the impact of an non-ideal channel could not be ignored any longer. A BPSK-Like model which takes the non-ideal channel into consideration is set up and a theoretically analysis is given. Three specific channels are used in order to testify the correctness. It can be conclude that a non-ideal phase-frequency response may have obvious influence on tracking bias whereas the impact on tracking accuracy is limited. Only non-ideal amplitude-frequency response may not influence the tracking performance.
0引言
在卫星导航系统中,导航信号由卫星生成并发射,经过空间传播并最终到达接收端进行处理,整个过程不可避免的会产生失真并对跟踪结果造成影响。随着对定位精度要求的不断提升,通道非理想的影响已不能忽略。下一代卫星导航系统中广泛采用的BOC信号由于带宽更宽,相比于传统BPSK调制的导航信号受通道的影响会更大。
针对非理想通道下信号的跟踪性能这一问题,有不少学者进行了研究。文献[1]给出了通道非理想下信号特性的评价指标,并针对七种具体类型的通道给出了各指标的理论推导及仿真验证结果。文献[2]从相关函数入手,研究了BPSK信号、低阶BOC信号以及高阶BOC等多种导航信号经过非理想通道后的信号特性。但这两篇文章并未给出通道对码跟踪性能影响的直接结论。文献[3]~[6]从仿真的角度分析了几种特殊通道下BPSK信号码跟踪性能,缺少理论支撑。文献[7]从理论上进行推导,指出经过非理想通道后的相关函数是理想相关函数同滤波器冲击响应的卷积且可以通过贝塞尔展开表示为理想相关函数的平移和叠加,此外还通过仿真得出了线性及非线性滤波器下的码跟踪偏差。但仍然没有从理论上就通道非理想对码跟踪性能的影响给出结论。文献[8]建立了非理想通道下的信号模型,从理论上分析了冲击响应为实函数时相干及非相干鉴相器下的码跟踪精度及跟踪偏差。文献[9]将通道类型由实函数扩展至复函数,理论分析并仿真验证了不同通道下的码跟踪偏差。上述分析大都针对于传统的BPSK信号,得出的结论对新体制BOC信号可能并不适用。此外,针对BOC信号的无模糊码跟踪算法有很多,如Bump-Jump算法[10]、边带跟踪(BPSK-Like)算法[11-12]、ASPeCT算法[13]以及双环路跟踪(Double Estimator)算法[14-15]等,不同算法对相同通道的反应也有可能不同。
针对上述问题,本文选择实现复杂度低且应用较为广泛的BPSK-Like算法,对考虑通道作用的BPSK-Like算法原理进行了详细的描述,从理论上对非理想通道下信号的码跟踪性能进行分析,并通过仿真对结论进行验证。
1BPSK-Like算法基本原理
边带跟踪算法是将接收到的BOC(m,n)信号看作中心频率偏移载波频率±m×1.023MHz的两路BPSK(n)信号之和,在接收时只将某一边带的信号同本地生成的参考BPSK信号进行相关,进而得到单一峰值的相关函数。
图1为考虑通道作用时边带跟踪算法的实现框图。
联系人: 张岩 E-mail: 15319043808@163.com
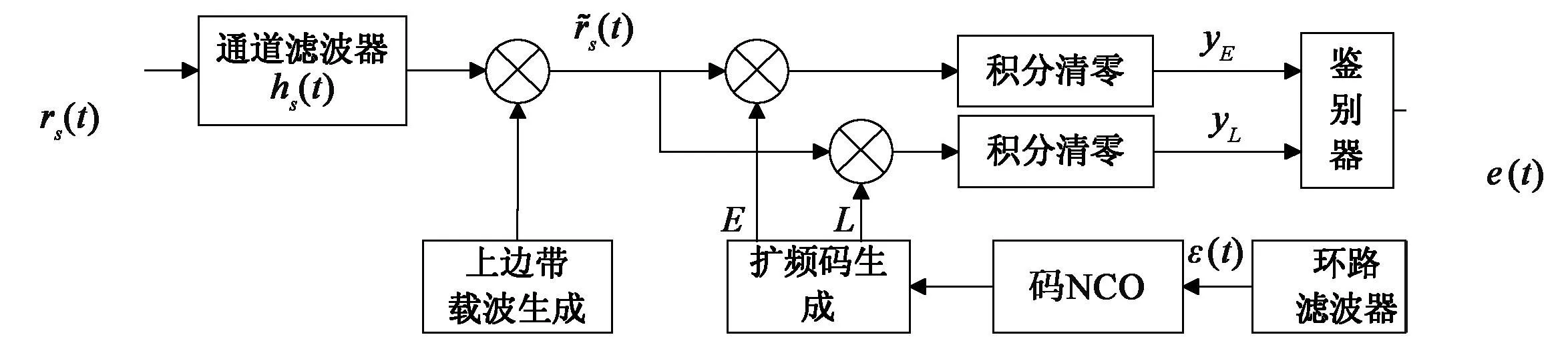
图1 边带跟踪算法实现框图
图中:hs(t)为等效的通道滤波器; yE与yL分别为码环早迟支路经过积分清除环节后的输出信号。本文分析假设载波剥离完全,即Q支路只包含有噪声分量。同时假设二支路上的噪声分量服从相同的统计分布规律。
2BPSK-Like算法性能分析
假设接收到的理想基带信号为(在预检积分时间内调制电文不发生变化,这里略去调制电文)
(1)
式中: P表示信号功率; c(t)表示伪随机码; sc(t)表示方波副载波; n(t)表示双边功率谱密度为N0/2的高斯白噪声,这里假设载波剥离完全。
当接收机带宽较窄时,经过频谱搬移的单边带BOC信号可以看作较为理想的BPSK信号,即
(2)
式中,fsc为副载波频率。于是经过通道及频谱搬移后的BOC信号为
rs(t) ≈rs(t)·hs(t)·sin(2πfsct)
sin(2πfsct)+ο(4πfsct)
(3)
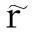
=XE+NE,
(4)
式中,
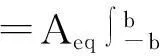
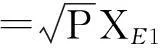
(5)
(6)
(7)
另一方面,
(8)
由于n(t)为高斯白噪声,对其进行频谱搬移不影响其性质,故上式NE可以简化为
(9)
进一步可以得到NE的相关函数为
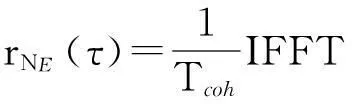
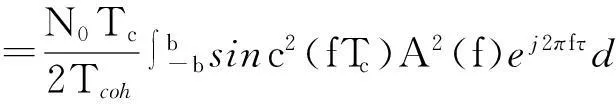
(10)
同理可得:
yL=XL+NL,
(11)
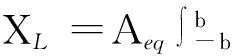
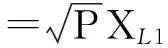
(12)
式中,Aeq同式(6)中的定义一致。
码跟踪环中的早迟支路的噪声服从相同的统计特性,统一用rN进行表示。
通常而言,环路的跟踪性能由码跟踪精度及码跟踪偏差两项指标进行衡量。其中,跟踪精度定义为处于稳定跟踪状态时ε(t)的方差,跟踪偏差定义为稳定跟踪状态时ε(t)的均值。将分别对这两项指标进行计算。
2.1 跟踪精度
假设图1中环路滤波器的带宽为BL,则经过平滑后的码跟踪精度可以定义为[1]
(13)
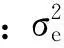
以非相干早减迟功率鉴相器为例,计算图1中鉴别器的输出信号e(t).
(14)
式中,
(15)
T2=2(XENE-XLNL),
(16)
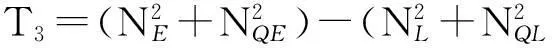
(17)
上式中T1控制鉴别误差曲线的形状(即鉴别曲线在过零点附近斜率K),T2、T3控制鉴相器输出量e(t)的方差。于是有:
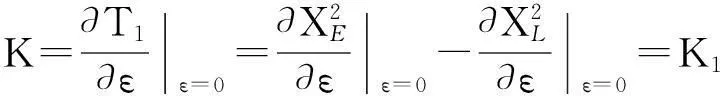
(18)
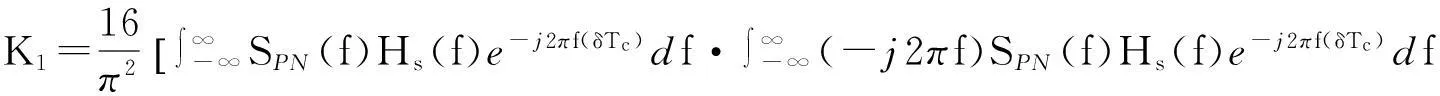
(19)
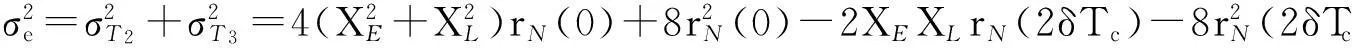
(20)
于是得到考虑通道作用下BPSK-Like算法的码跟踪精度为(记CN0=P/N0)
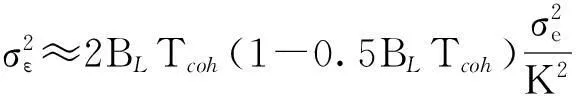
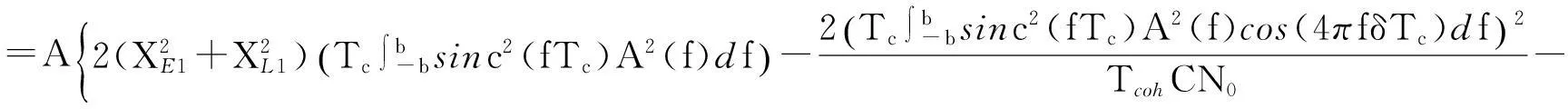
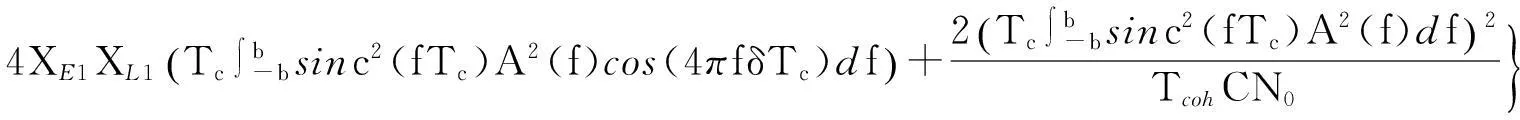
(21)
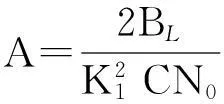
2.2 跟踪偏差
跟踪偏差即是求解E[ε(t)]=0时ε的值。
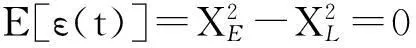
(22)
即要求下式成立
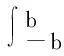
sin(2πfδTc)df=0,
(23)
当ε在0附近时,对上述结果在ε处进行泰勒级数展开并取一阶项有
(24)
3仿真验证
上文对通道非理想条件下的码跟踪精度及跟踪偏差进行了理论分析,下面分别从理想情况、幅频响应非理想及相频响应非理想三个方面对上述结论进行验证,并得出通道特性对BPSK-Like算法码跟踪性能的影响。
3.1 理想通道
理想带限低通滤波器的频率特性可以表示为
A(f)=1,τg(f)=0.
图2示出了理想通道下早迟码间隔分别取0.1 chip及1.0 chip时的跟踪偏差随时间的变化关系。其中,信噪比CN0=40 dBHz,码环噪声带宽BL=2 Hz,相干积分时间Tcoh=1 ms,码片周期Tc=1/1023000 s.
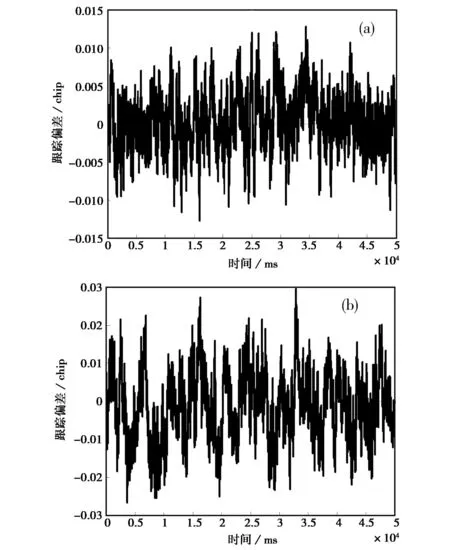
图2 理想情况跟踪结果 (a) d=0.1 chip; (b) d=1.0 chip
表1分别示出了仿真与理论推导得出的码跟踪精度及码跟踪偏差。
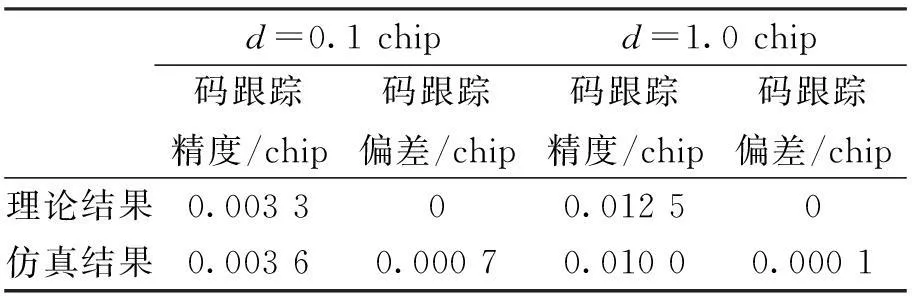
表1 理想情况不同早迟码间隔下仿真及
可以看出,理论推导结果同仿真结果基本吻合。理想情况下,早迟码间隔越小跟踪精度越高。
3.2 幅频响应非理想
以二次曲线型幅频响应为例,对幅频响应非理想情况下的码跟踪性能进行研究。二次曲线型幅频响应滤波器的幅频响应和相频响应分别为
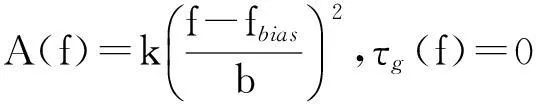
(25)
其中,k表示波动的幅度,频率f关于b归一化。当k值越大b值越小时表示群时延的波动越剧烈。fbias表示二次曲线的中轴偏离0的大小。
如图3所示为二次曲线波动幅度k=0.15 chip以及k=1.5 chip时的相关函数形状(滤波器单边带宽b=10.23 MHz).
可以看出,二次曲线型幅频响应通道对相关函数的形状及位置并无明显影响。如图4所示,以k=0.15 chip为例,对比早迟码间隔分别取0.1 chip及1.0 chip时的跟踪偏差随时间的变化关系。
表2分别示出了仿真与理论推导得出的码跟踪精度及码跟踪偏差。
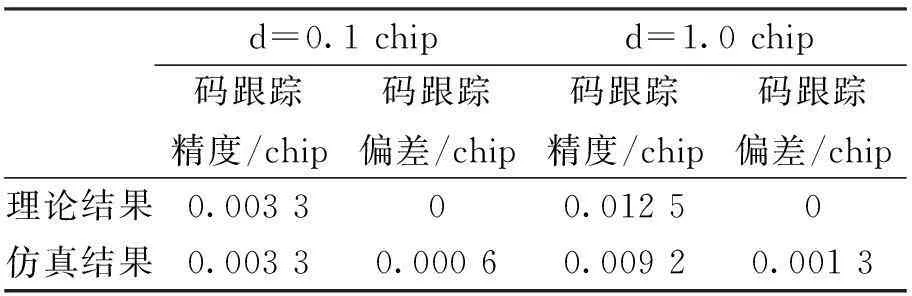
表2 幅频响应非理想不同早迟码间隔下仿真
可以看出,二次曲线型幅频响应非理想通道下的跟踪性能同理想情况下基本类似,当早迟码间隔较小时跟踪精度相对较高,且可以认为不会产生跟踪误差。
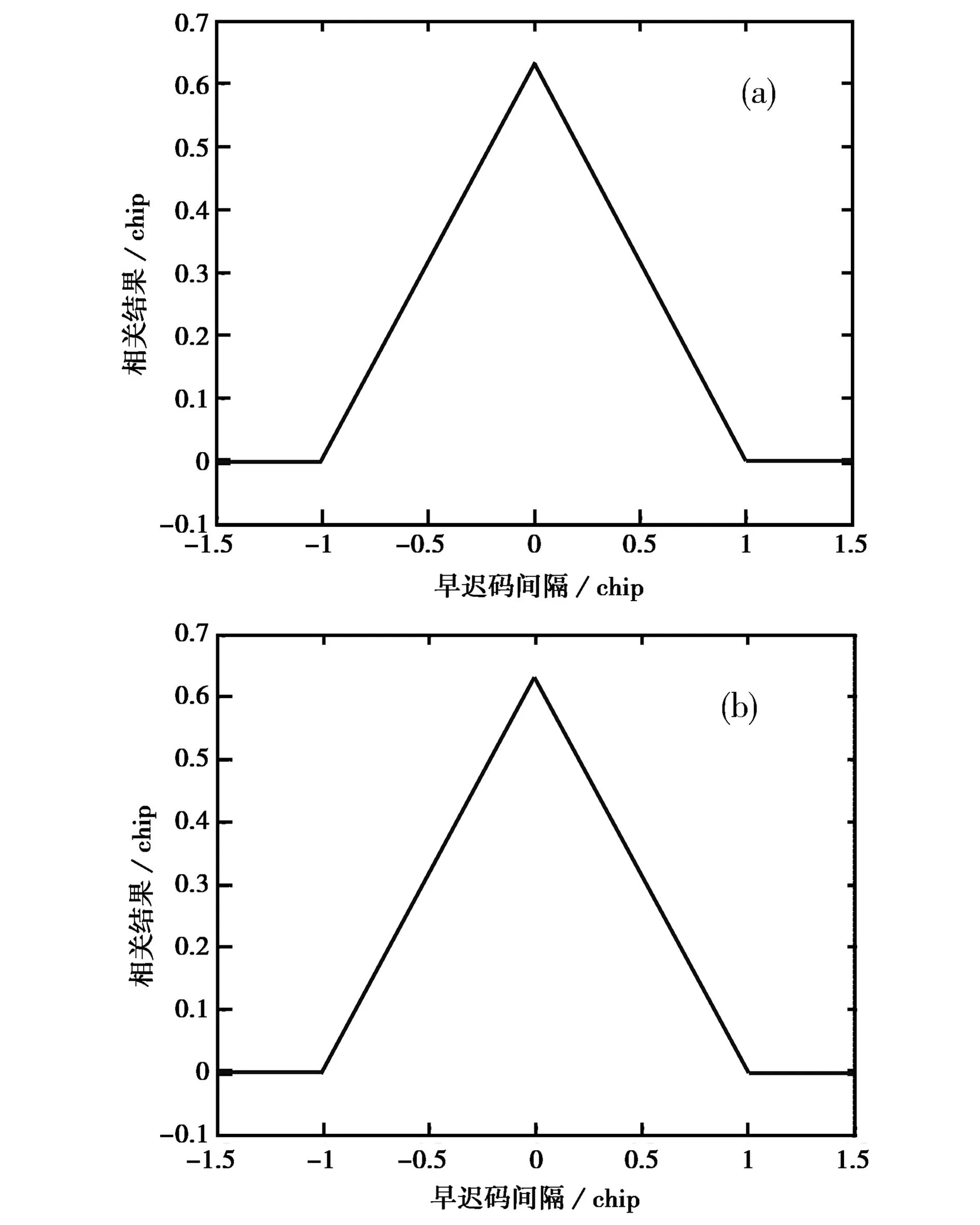
图3 二次曲线幅频响应相关函数形状 (a) k=0.15 chip; (b) k=1.5 chip
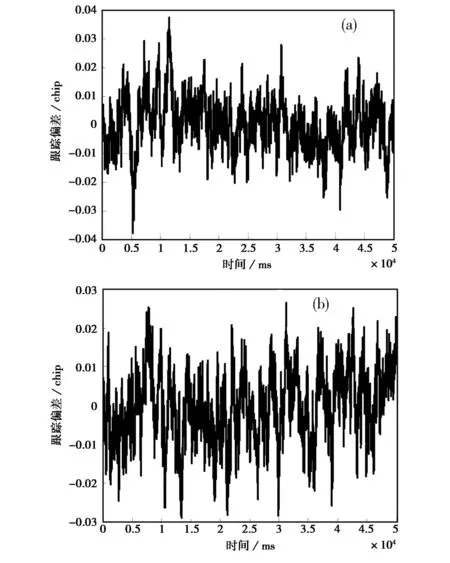
图4 二次曲线幅频响应跟踪结果 (a) d=0.1 chip; (b) d=1.0 chip
3.3 相频响应非理想
以二次曲线型群时延为例,对相频响应非理想情况下的码跟踪性能进行研究。二次曲线型群时延滤波器的幅频响应和相频响应分别为
A(f)=1,
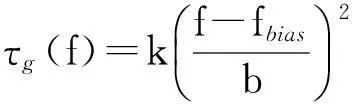
(26)
其中,k表示群时延波动的幅度,频率f关于b归一化。当k值越大b值越小时表示群时延的波动越剧烈。fbias表示二次曲线的中轴偏离0的大小。
如图5所示为群时延波动幅度k=0.15 chip以及k=1.5 chip时的相关函数形状(滤波器单边带宽b=10.23 MHz)。
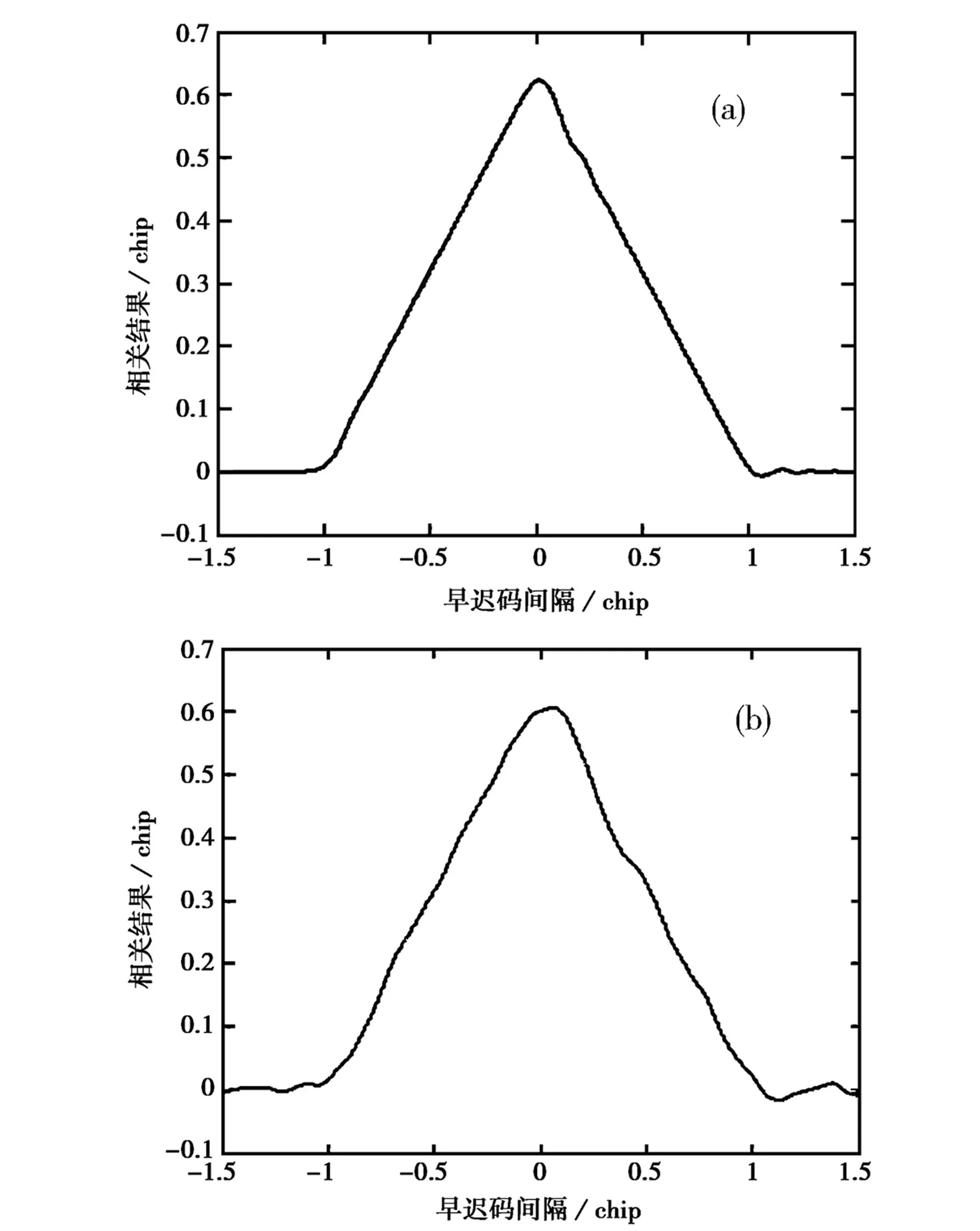
图5 二次曲线群时延相关函数形状 (a) k=0.15chip; (b) k=1.5chip
可以看出,群时延波动幅度越大,信号经过通道后相关函数的变形就越严重。
以k=0.15 chip为例,对早迟码间隔分别取0.1 chip及1.0 chip时的跟踪偏差随时间的变化关系进行对比,如图6所示。
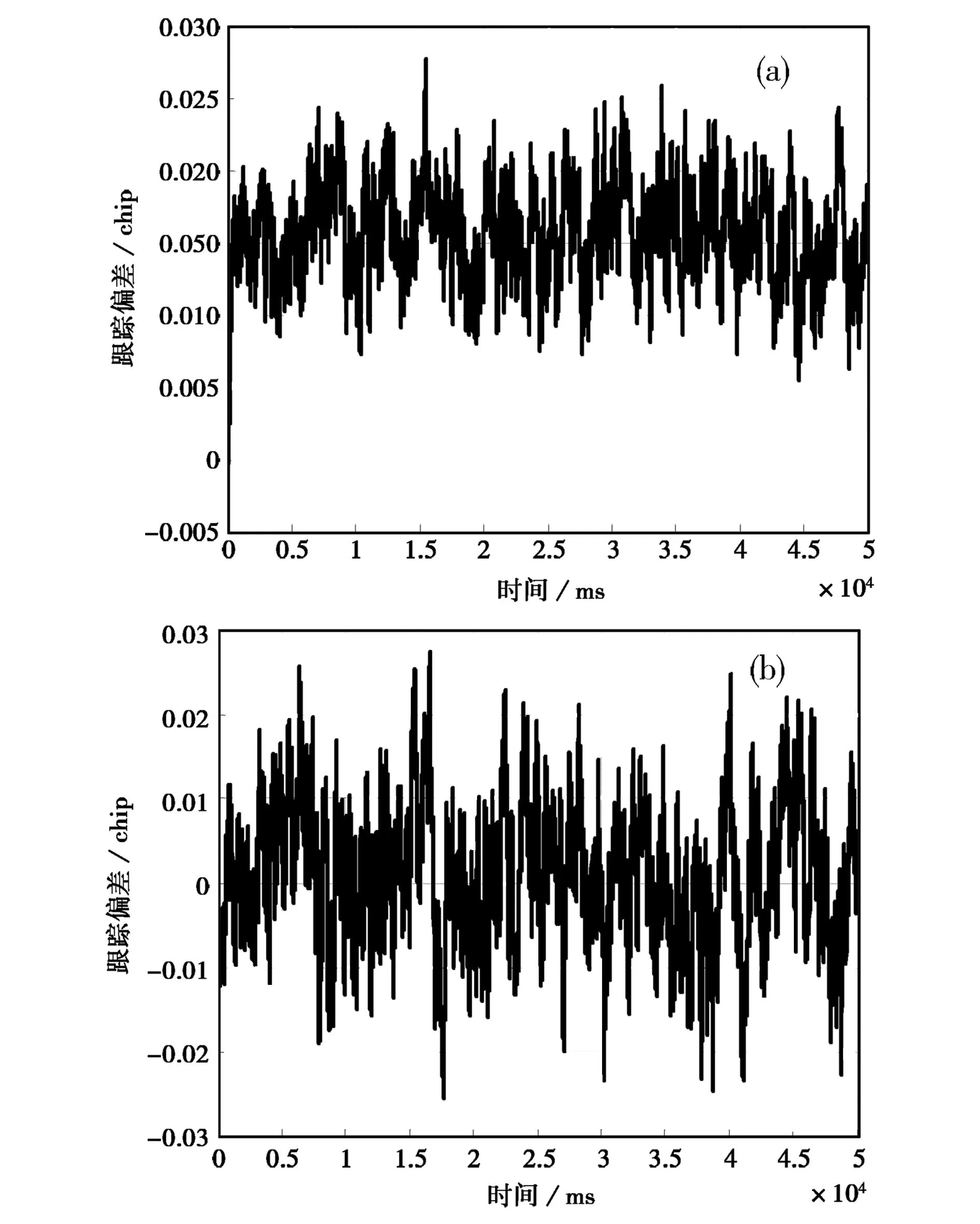
图6 二次曲线群时延跟踪结果 (a) d=0.1 chip; (b) d=1.0 chip
表3示出了仿真与理论推导得出的码跟踪精度及码跟踪偏差。
通过上述三种情况下的仿真验证了对通道非理想条件下BPSK-Like算法跟踪性能影响的理论推导的正确性。同时也可以得出结论:幅频响应非理想不会对跟踪性能产生影响;相频响应非理想会产生跟踪偏差,偏差量的大小同具体通道特性有关,但对跟踪精度的影响不大。
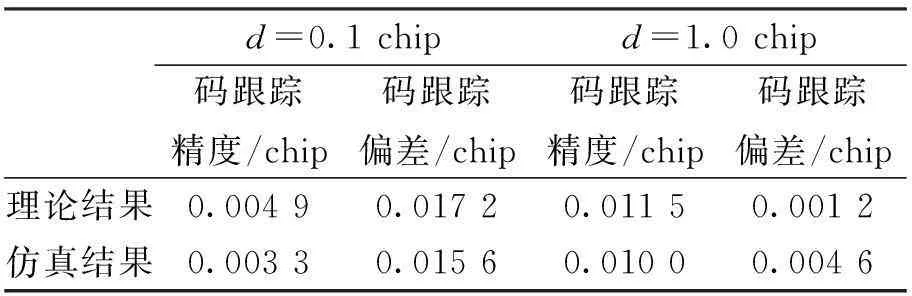
表3 相频响应非理想不同早迟码间隔下仿真及
4结束语
本文推导了通道作用下BPSK-Like算法的跟踪性能,并通过仿真验证了理论推导的正确性,得出了通道非理想对码跟踪性能影响的一些结论。文章指出,相频响应非理想对相关函数形状、位置以及码跟踪性能的影响要远大于相同波动幅度的幅频响应对上述量的影响。通道的非理想特性主要影响码跟踪偏差,对码跟踪精度的影响较小。
参考文献
[1] SOELLNER M, KOHL R, LUETKE W,etal. The impact of linear and non-linear signal distortions on Galileo code tracking accuracy[C].//Proceedings of the ION GPS, 2002.
[2] BETZ J W. Effect of linear time-invariant distortions on RNSS code tracking accuracy[C].//Proceedings of the ION GPS, 2002.
[3] 田嘉,王伟,史平彦. 群时延对测距误差的影响[J]. 空间电子技术,2012(3):14-16.
[4] 余宜珂,王萌,郭伟,等. GNSS接收机中频带通滤波器群时延对伪距测量影响的研究[J]. 电子测量技术,2014,37(3):24-28.
[5] 耿虎军. 系统群时延特性对伪码测距影响的研究[J]. 无线电工程,2004,34(11): 27-29.
[6] 朱峰,李孝辉,王国永. 滤波器群时延分析及其对导航信号的影响[J]. 电子测量技术,2013,36(5):54-57.
[7] 钱世杰,帅涛,李国通. 滤波器群时延特性对伪距测量的影响[J]. 遥测遥控,2012,33(5):41-46.
[8] 许晓勇. 卫星导航接收机高精度建模、分析及优化设计研究[D]. 长沙:国防科学技术大学,2008.
[9] 李柏渝,陈雷,李彩华,等. 通道非理想特性对导航接收机伪码测距零值的影响分析[J]. 电子与信息学报,2011,33(9):2138-2143.
[10]FINE P, WILSON W. Tracking algorithm for GPS offset carrier signals[C].//Proc. of the ION International Technical Meeting, 2010:859-871.
[11]BAKER B C. Overview of the GPS M code signal[C].//Proceedings of the Insititute of Navigation, Ananheim,California, 2000:542-549.
[12]MARTIN N, GUICHIN H,HOLLREISER M,etal. Acqisition of the PRS BOC(15,2.5) signal in presence of multi-path[C].//NAVITEC 2008, 2008.
[13]JULIEN O, MACABIAU C, CANNON M E,etal. ASPeCT: Unambiguous Sine-BOC(n,n) acquisiton/tracking technique for navigation applications[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007,43(1):150-162.
[14]HODGART M S, BLUNT P D, UNWIN M. Double estimator:A new receiver principle for tracking BOC signals[J]. Inside GNSS,2008:20-29.
[15]HODGART M S, SIMONS E. Improvements and additions to the double estimation technique[C].//Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing, (NAVITEC), 2012 6th ESA Workshop on,2012.
张岩(1991-),女,硕士生,主要研究方向为卫星导航信号处理。
刘瀛翔(1986-),男,博士,主要研究方向为卫星导航信号处理。
唐小妹(1981-),女,博士,副研究员,主要研究方向为卫星导航信号处理。
孙广富(1969-),男,博士,研究员,主要研究方向为卫星导航信号处理。
The Impact of Non-Ideal Channel on Tracking
Performance of BPSK-Like Method
ZHANG Yan,LIU Yingxiang,TANG Xiaomei,SUN Guangfu
(SatelliteNavigationandPositioningR&DCenter,SchoolofElectronicScienceand
Engineering,NationalUniversityofDefenseTechnology,Changsha410073,China)
Key words: Binary offset carrier modulation; BPSK-Like; non-ideal channel; tracking performance
