基于高度角的GNSS-R测高精度及反射事件数量研究

基于高度角的GNSS-R测高精度及反射事件数量研究

胡长江1，王磊2

(1.常德市国土资源规划测绘院,常德 415000;2.立得空间信息技术股份有限公司,武汉 430070)

摘要：从现有的GNSS-R(GNSS Reflectometry)测高理论出发,得出了测高精度会随高度角的减小而降低的结论,并分析了优于4 m的测高精度需要满足高度角大于31°的条件;在一组实际实验数据中,优于4 m的测高精度需要满足高度角达到38°,考虑到实际情况受到海风、海面粗糙度等因素的影响,实验结论与理论值是一致的。 以高度角需要满足的该条件为基础,对测高事件数量进行了研究,并将其与其他学者采用的截止高度角(15°、20°)进行了对比,得出高度角提高到38°后,事件数量将减少50%左右的结论。

关键词：GNSS-R测高;高度角;反射事件

doi:10.13442/j.gnss.1008-9268.2015.05.005

中图分类号：P228

文献标志码：A

文章编号：1008-9268(2015)05-0025-05

收稿日期：2015-07-07

作者简介

Abstract:Based on the present theories of GNSS-R(GNSS Reflectometry)altimetry, the conclusion that the precision of GNSS-R altimetry declines with the decrease of elevation angle is achieved. Furthermore, the elevation angle needs to meet the condition of over 31° if a result of better than 4-m-precision wants to be obtained. In a set of actual experimental data, elevation angle needs to be at 38° for better than 4-m precision. Given that actual data is detrimentally affected by factors, such as ocean wind; sea surface roughness and so forth, the experimental result is in line with theoretical conclusion. By employing the condition elevation angle meets, the impact of elevation angle on the amount of reflection events is studied. In comparison with cutoff elevation angle used by other researchers (15°and 20°), the mount of data will decrease by some 50% in this paper..

0引言

从GNSS-R测高这一概念的提出到现在已有20多年[1],这一领域的学者和专家在理论和实验方面都做了大量的工作,取得了很多突破性的成果。在岸基和机载实验中,已经获得了厘米级的测高精度[2,3],在星载方面,虽然目前缺乏这方面的数据,但西班牙空间科学研究所的Cardellach等通过对观测量的残差进行建模,预测了星载测高可获得空间分辨率为65 km、测高精度为22 cm的结果[4]。在理论方面,Hajj和Wagner等研究了星载GNSS-R测高中反射事件的分布、密度等问题,研究表明星载测高事件的密度比卫星测高的事件密度要高一个数量级[5-6]。

在GNSS-R测高中,虽然目前已经获得了厘米级的测高精度,但经常是通过增长非相干积分时间(损失空间分辨率)或挑选较高高度角的事件(剔除大量数据)得到的[4,7]。而在研究反射事件密度时,设定的截止高度角通常较小(如15°、20°)[5-6],这与获得高精度的测高结果不一致。为了兼顾测高精度和数据利用率以及更合理地评估反射事件数量,需要量化地讨论截止高度角的问题,但目前并没有针对该问题进行研究的文献。因此,本文首先以1 ms~1 s的相干积分-非相干积分信号处理策略为例,分析了用C/A码测高时,要达到优于4 m的测高精度,高度角需要满足的条件;然后以该结论为基础,讨论了当考虑测高精度时,截止高度角对反射事件数量的影响。

1GNSS-R测高精度与高度角关系

本节在讨论GNSS-R测高与高度角的关系时,是以接收机平台较低(岸基或机载)的情况为例的,这样便于用相应的实验数据对理论进行验证。这种情况下的测高表达式为[8]

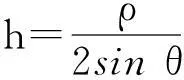
(1)

式中: h为海面相对参考面的高; ρ表示反射信号相对直射信号的路径延迟; θ表示镜面反射点的卫星高度角,本文中的高度角都是指镜面反射点的卫星高度角。

资助项目： 国家重大科学仪器设备开发专项项目(编号：2012YQ160185)

联系人： 胡长江E-mail:1050413737@qq.com

为了分析测高精度与高度角的关系,对式(1)求全微分可得到测高精度的表达式为

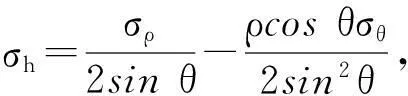
(2)

将式(1)代入式(2)消去ρ得到式(3)

(3)

其中高度角的精度可以达到10-5rad以上[8-9],而接收机平台高度一般只有几千米,考虑到路径延迟测量精度为米级,因此式(3)右边的第二项相对第一项可以忽略。所以可以得到简化的测高精度表达式为

(4)

由式(4)可知,假设在一定观测时段内,延迟测量精度σρ变化不大,则测高精度会随高度角的减小而迅速降低。接下来讨论的是要想获得合理的测高精度(如优于4m),高度角要满足怎样的条件。

路径延迟是反射信号路径ρR与直射信号路径ρD之差,即

ρ=ρR-ρD.

(5)

C/A码的测距精度若以码片长度的1/100计算,则为2.93m,即ρD的精度为2.93 m,考虑到反射信号比直射信号要弱,而且反射信号的到达时刻没有直射信号(相关峰值处)稳定,那么ρR的精度不可能高于ρD,即σR要大于2.93 m,结合误差传播定律有

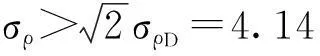
(6)

若要获得4m的测高精度,将式(6)代入式(4)中可得高度角应满足如下条件:

θ>31°.

(7)

2实验分析

为了对上述理论推导的结论进行验证,本文将对法国国家太空研究中心CNES资助的CAROLS09机载实验进行分析,该实验于2009年4月27日至5月28日进行。表1给出了对本文所采用数据的描述。在提取反射信号相对直射信号路径延迟时,本文采用的是变化率最大法[10]。

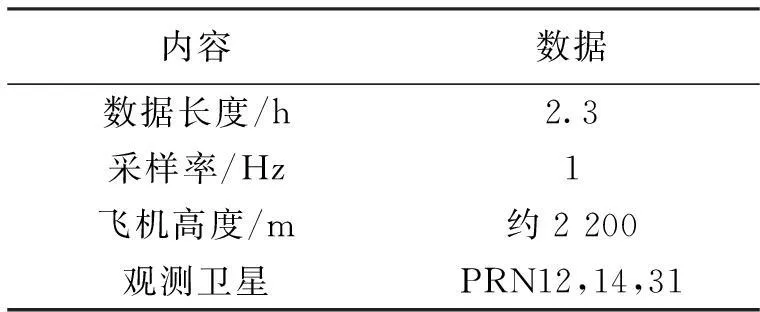
表1　实验数据描述

图1是在观测时段内,用于GNSS-R测高卫星(PRN12、14和31)的高度角变化示意图,从图中可以看出,PRN14号卫星在观测时段内,其高度角在[20,52]°范围内变化,有一个先增大后减小的过程;PRN12号卫星的高度角从80°逐渐降低到30°以下;而PRN31号卫星的高度角从10°增大到55°左右。三颗卫星的高度角跨度为10°到80°,对高度角的区间[0,90]°进行了对大部分的覆盖。

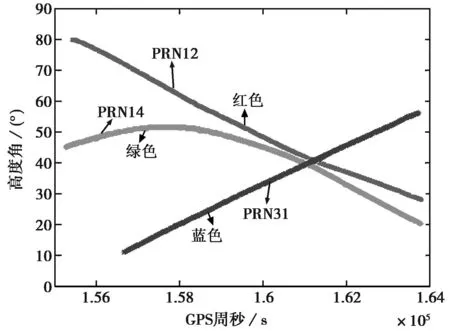
图1　高度角变化示意图

如图2、3和4分别是PRN12、14和31号卫星的测高精度与高度角的关系图,本文按时间先后顺序用1°的区间(如[21.00,21.99]°)将测高的结果进行分开,然后分别计算它们在每个高度角区间的精度,其中,横坐标表示高度角,纵坐标表示测高的精度。当高度角很低时(如小于20°),测高的精度非常差,达到数十米甚至百米级,造成这种结果的主要原因是:1) 由(4)式所导致的;2) 当高度角很低时,散射现象非常明显,会导致反射信号质量变差,从而很难提取准确、稳定的路径延迟。为了更清晰地反映高度角较大时,测高精度的变化情况,将上述三幅图都进行了局部放大,局部图中红色离散的点表示对应高度角的测高精度,绿色的点实线是将这些散点拟合的结果，这样能更直观的反映变化趋势。蓝色的垂直和水平虚线标出了测高精度为4 m的高度角位置。

从三幅图中都可以清楚地看到,随着高度角的增大,测高精度逐步提高,这与前面理论推导的结论是完全一致的。从图2可以看出,该颗卫星中高度角等于36°时,达到了4 m的测高精度。如图4所示，在PRN31号卫星中,当高度角等于37°时,测高精度能够达到4 m.对于PRN14号卫星(如图3),4 m的测高精度需要42°的高度角,这三个高度角不同范围地高出了式(7)中的31°,这是因为在推导式(7)的过程中,无法考虑海风、海面粗糙度、反射信号强度衰减等因素对测高精度的影响,而实际情况中会不同程度地受这些因素的影响,因此,在排除误差后,实验的结果与理论结果是一致的。

另外,如图1所示，PRN14号卫星,高度角两次经过区间[45,52]°,图3的局部放大图中的红色虚线方框将不同时间出现的[45,52]°的测高精度标示了出来,从红色方框可以看出,每个高度角都对应两个测高精度(不同时间),需要指出的是,同一高度角的两个测高精度大小很相近,这也说明了在该实验中,高度角与测高精度之间不仅存在稳定的趋势关系,而且还存在较稳定的大小对应关系。

最后,为了充分考虑测高精度与高度角在实际情况中的变化关系,本文将实验中三颗卫星的截止高度角取平均(即38°)作为1 ms~1 s的相干积分-非相干积分信号处理策略达到优于4 m测高精度的截止高度角,而不是理论上的31°.需要指出的是,当采用38°的截止高度角时,总体的测高精度会优于4 m(因为高度角越高,精度越高),这与其他学者采用相同的码和信号处理策略所获得的3.37 m的测高精度相比[4],是非常吻合甚至可能更优的。

3反射事件与高度角

目前在研究GNSS-R测高优势时,通常将其反射事件与卫星测高的反射事件进行密度的对比,而在选择GNSS-R测高数据时,截止高度角一般选得较低,没有考虑测高精度的因素,而卫星测高也可以看成比较特殊的GNSS-R测高(当高度角接近90°时),具有很高的测高精度,这种评估策略显然不够合理,为此,本文将引入考虑测高精度的截止高度角,并进行初步的相关研究。

当前在理论上研究GNSS-R测高反射事件的数量都是针对星载模式的,这是为了评估星载测高的潜力。由于当前缺乏星载实验数据,前面几部分研究的截止高度角都是针对低平台的情况,但考虑到星载模式下,反射信号将更弱,情况更复杂,要想获得同样优于4 m的测高精度,对高度角的大小将有更高的要求,即星载模式下的截止高度角将大于38°。需要指出的是,前面的理论分析是基于机载和岸基的情况,其结论不能直接用于星载情况,因为星载模式具有不同的测高几何模型。本文在此以38°为截止高度角进行初步研究,并将其与其他文献中采用的10°、15°进行反射事件数量的对比。

本文将采用仿真数据对该问题进行研究,仿真数据的说明如表2所示。在选择仿真数据时,尽可能地考虑了接收机平台高度及发射机轨道面的多样性。

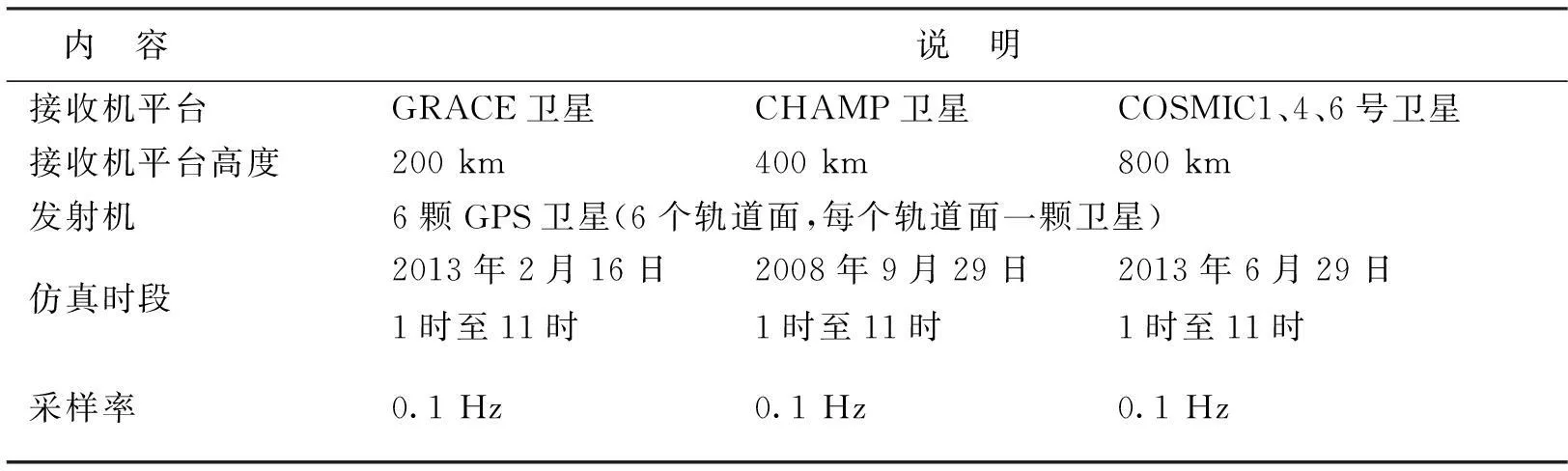
表2　仿真数据描述

表3示出了仿真数据的实验结果,表中给出的是截止高度角设为38°时,反射事件数量分别相对15°和20°减少的百分比。第二行第四列的69%表示当截止高度角为15°时,若反射事件有100个,那么当高度角设为38°时,反射事件只有31个,损失了69个。将这些数据分别取平均,得到高度角38°相对20°,事件减少49.86%;相对15°,事件减少56.89%.

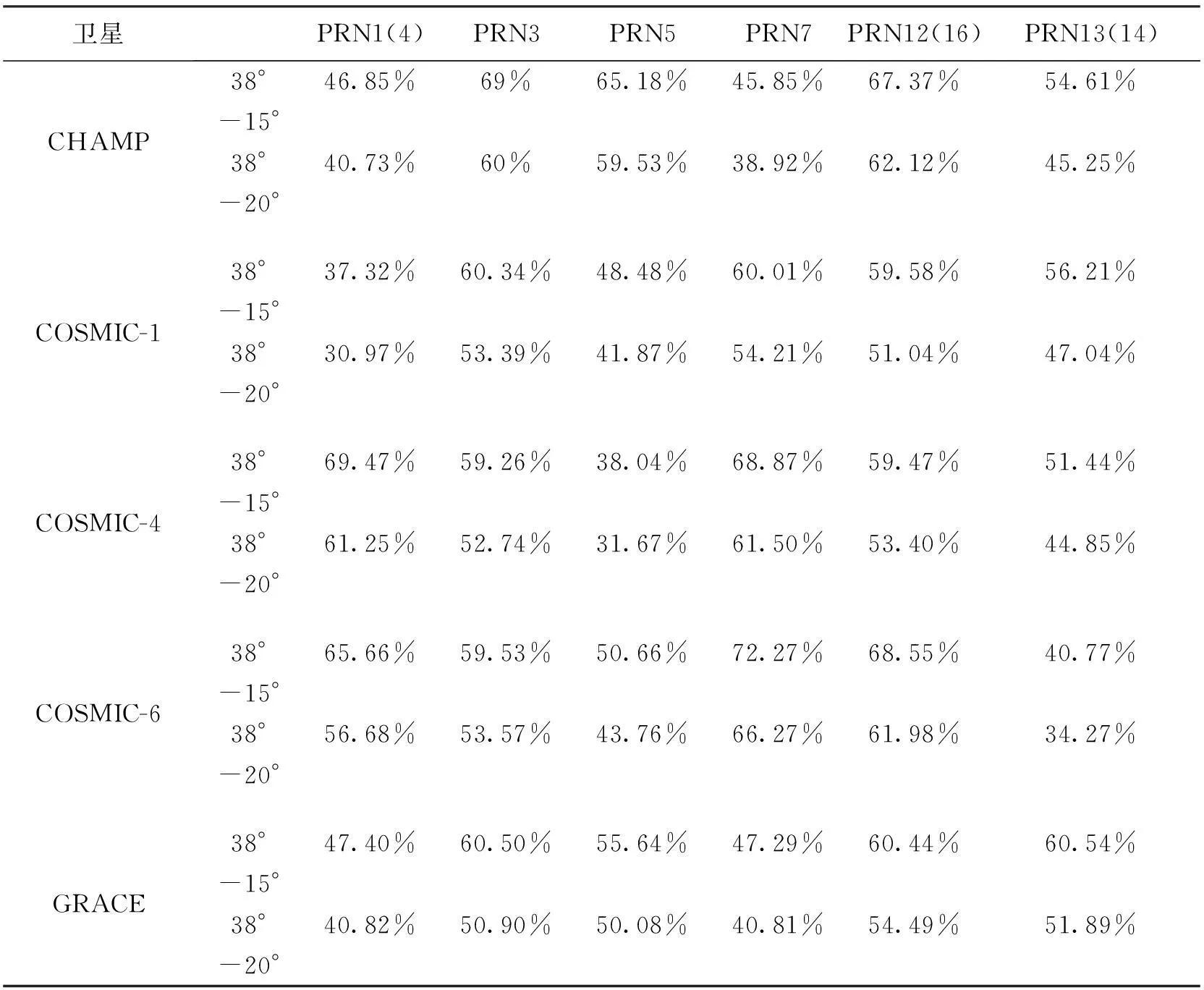
表3　38°截止高度角相对15°和20°损失反射事件的比例

提高截止高度角对反射事件减少量的影响主要与事件随高度角的分布有关,以本文的实验为例,当截止高度角增加到38°时,反射事件相对15°、20°减少了50%左右,这说明本实验中有近一半的数据分布在[15,38]°之间,而这部分数据不利于达到预期的测高精度。从本实验可以看出,提高截止高度角会显著性地影响反射事件利用率。若要提高反射事件利用率,可以从以下两方面进行提高:1) 通过利用其它码信号、改进算法等来降低截止高度角;2) 通过对接收机平台的设计,提高反射事件在高高度角区间分布的比例。

4结束语

通过本文的理论研究和实验分析,可以得出以下几方面结论。当测距精度变化不大时,GNSS-R测高精度会随高度角的降低而逐渐下降;为了量化预期的测高精度与截止高度角之间的关系,本文以C/A码、1 ms~1 s的相干积分-非相干积分信号处理策略为例,分析得出要想达到优于4 m的测高精度,高度角应大于38°的结论,该值可以作为筛选GNSS-R数据的一个参考条件;当截止高度角设为38°时,相对其他文献采用的15°与20°来说,会对反射事件的利用率产生很大的影响,在本文的实验中,反射事件数量减少一半左右,这是不利于测高精度提高的,因为在实际应用中,局部海域的高通常是将该区域所有事件的测高结果取平均得到的,从这个角度上讲,事件数量的增加是有利于测高精度的提高的,而本文理论分析部分是针对单个事件而言的,目的在于为筛选数据提供依据。

参考文献

[1] MARTIN-NEIRA M. A passive reflectometry and interferometry system(PARIS):Application to ocean altimetry[J]. ESA Journal,1993(17):331-355.

[2] TREUHAFT R N,LOWE S T,ZUFFADA C,etal. 2-cm GPS altimetry over crater lake [J].Geophysical Research Letters,2001，22(23):4343-4346.

[3] LOWE S T,ZUFFADA C,CHAO Yi,etal. 5-cm-Precision aircraft ocean altimetry using GPS reflections[J].Geophysical Research Letters, 2002,29(10):1375-1378.

[4] CARDELLACH E, RIUS A, MARTIN-NEIRA M,etal. Consolidating the precision of interferometric GNSS-R ocean altimetry using airborne experimental data[J].IEEE Transactions on Geoscience and Remote Sensing, 2014,52(8): 4992-5004.

[5] HAJJ G A, ZUFFADA C. Theoretical description of a bistatic system for ocean altimetry using the GPS signal[J].Radio Science, 2003,38(5):1089.

[7] RIUS A, CERVELLERA F, RIBO S,etal. Paris interferometric technique proof of concept: Sea surface altimetry measurements[J]. IEEE IGARSS, 2012：7067-7070.

[8] 杨东凯,张其善. GNSS反射信号处理基础与实践[M].北京:电子工业出版社, 2012:129-153.

[9] 胡长江,李英冰.全球导航卫星反射信号的镜面反射点算法[J].测绘科学,2014,39(12):33-35.

[10]RIUS A, CARDELLACH E, MARTIN-NERA M. Altimetric analysis of the sea-surface GPS-reflected signals[J].IEEE Transactions on Geoscience and Remote Sensing, 2010,48(4):2119-2127.

胡长江(1990-),男,湖南澧县人,硕士,主要从事GNSS-R测高研究。

王磊(1988-)，男，湖北襄阳人，硕士，主要从事惯性导航方面的研究。

Research on the Precision of GNSS-R Altimetry and the Amount of

Reflection Events Based on Elevation Angle

HU Changjiang1,WANG Lei2

(1.InstituteofPlanningandMappingofLandResourcesofChangde,Chanagde415000,China;

2.LeadorSpatialInformationTechnologyCo.,Ltd.,Wuhan430070,China)

Key words: GNSS-R altimetry; elevation angle; reflection events