北斗系统混合星座对DOP值和RDOP值的影响分析

北斗系统混合星座对DOP值和RDOP值的影响分析

陈正坤,刘文祥,苏映雪,王飞雪

(国防科学技术大学电子科学与工程学院卫星导航定位技术工程研究中心,长沙,410073)

摘要：分析了GPS和北斗区域系统在(55°S~55°N,55°E~180°E)区域内DOP值和RDOP值的分布特点,探讨了可见卫星数、基准卫星变化、基线长度和基线方向对两类精度因子值一致性的影响关系。实验结果表明:北斗系统在中长基线相对定位中应使用RDOP值进行预报和精度分析。

关键词：北斗系统;混合星座;DOP值;RDOP值

doi:10.13442/j.gnss.1008-9268.2015.05.002

中图分类号：P228.4

文献标志码：A

文章编号：1008-9268(2015)05-0007-07

收稿日期：2015-06-12

作者简介

Abstract:This paper analyzes the distribution features of GPS and BDS DOP and RDOP within the region (55°S~55°N,55°E~180°E), and discusses the influence for the consistency of double precision factor with the number of visible satellites, the changes of reference satellite, the baseline direction and baseline length. The experiment results show that it should use the RDOP to forecast and analysis the long baseline relative positioning with BDS.

0引言

在导航学中用于定位精度分析的指标主要有:精度因子(DOP)和相对精度因子(RDOP),其值的大小主要取决于卫星星座相对于用户的空间分布[1]。北斗系统选择独特的混合星座设计方案,其卫星星座中除了中圆地球轨道(MEO)卫星,还包含地球静止轨道(GEO)卫星和倾斜地球同步轨道(IGSO)卫星[2],混合星座下的卫星空间分布会影响DOP值和RDOP值的变化,从而影响北斗系统定位精度的分析。

已有研究中,文献[3-4]推导了GPS中DOP值与RDOP值的数学公式,得到了两类精度因子值的相互关系;文献[5]仿真分析了南亚地区GPS和Galileo系统的DOP值,得出未来Galileo系统的定位精度较GPS更优;文献[6]提出了在混合星座导航系统中,使用测距误差加权几何精度因子能更准确地评估定位精度;但是目前对北斗系统DOP值和RDOP值分布特点及其一致性关系的研究较少。本文通过推导单点定位和相对定位精度因子值的表达式,结合混合星座的卫星空间分布特点,并利用实测数据分析GPS和北斗系统DOP值和RDOP值在(55°S~55°N,55°E~180°E)区域内的分布规律,最后探讨了两类精度因子值一致性

关系的影响因素。

1GNSS定位解算和精度分析

1.1　单点定位和相对定位原理

导航系统的基本观测量有伪距、载波相位和多普勒计数,其中伪距和载波相位的基本方程[1]为

P= ρ-(δtr-δts)·c+δion+

δtro+δmul+ε,

(1)

λ·Φ= ρ-(δtr-δts)·c-λ·

N-δion+δtro+δmul+ε,

(2)

其中: P和Φ分别为伪距和载波相位测量值; λ为载波的波长; ρ为卫星至接收机之间的几何距离; δtr和δts分别表示为接收机钟和卫星钟的钟差； r和s分别表示接收机和卫星编号; c为光在真空中的传播速度;N为整周模糊度值; δtion、δttro和δtmul分别表示为电离层误差、对流层误差和多路径误差;ε为测量噪声。在整周模糊度值已知或固定时,载波相位值可以等效成高精度的伪距值,本文只讨论伪距定位的情况。当可见卫星数n(≥4)时,单点定位观测方程可表示为

V1=A1·ΔΧ1-L1.

(3)

令卫星至接收机的方向向量为e=(x,y,z),上式中

联系人： 陈正坤 E-mail: czk25102@163.com

根据最小二乘准则,待定点坐标的解为

(4)

实际生产中通常采用相对定位来提高定位精度,即利用原始观测值在接收机之间和在卫星之间两次作差,组成的双差观测量既能消除接收机钟和卫星钟的钟差,还可以削弱电离层误差和对流层误差[1]。假设有2台接收机(基准站R和移动站U,其中R坐标已知),某一时刻共有m(≤n)颗共视卫星,通常选择高度角最大的卫星为基准卫星,令第m号卫星为基准卫星,构建单差和双差算子如下:

(5)

线性化后,可以得到相对定位双差观测方程为

V2=A2·ΔΧ2-L2,

(6)

上式中:

同理,由最小二乘准则可以得到方程(6)的解为

(7)

1.2　精度因子与定位误差分析

在定位精度分析时,通常假设各颗卫星的测量误差为正态分布,标准差为σUERE-j,并且不同卫星间的测量误差互不相关[1],得到方程(4)定位误差的方差为

(8)

同理,式(6)定位误差的方差[6]为

(9)

由式(7)和式(8)看出,在测量误差一定的情况下,定位误差的方差只与矩阵H1和H2有关,推导权系数矩阵在站心坐标系中表达式有

(10)

式中: R为空间直角坐标系至大地坐标系的转换矩阵[1],则北斗系统的DOP值和RDOP值可定义为

(11)

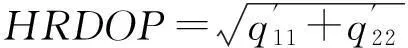
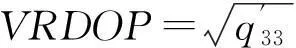
(12)

其中:HDOP为水平精度因子;VDOP为高程精度因子;PDOP为空间位置精度因子;HRDOP为水平相对定位精度因子;VRDOP为高程相对定位精度因子;PRDOP为空间位置相对定位精度因子。由此，根据精度因子的大小可以判断定位精度的高低,并且精度因子值越小,定位精度越高。本文选择PDOP值和PRDOP值作为研究对象,可以分析其在三维空间位置的定位精度。

2北斗系统混合星座下PDOP值和PRDOP值分析

2.1　北斗系统混合星座卫星空间分布

北斗系统采用混合星座设计,目前运行的北斗区域系统由5GEO+5IGSO+4MEO组成[7],其中5颗GEO卫星轨道高度为35 786km,分别定点于58.75°E、80°E、110.5°E、140°E和160°E;IGSO卫星轨道高度为35 786km,轨道倾角55°,其中6、7和8号星下点轨迹接近,交点位于118°E附近,9和10号星下点轨迹交点位于95°E附近;4颗GEO卫星轨道高度为21 000km,分别位于WALKER(24/3/1)星座的第一轨道面7、8相位和第二轨道面3、4相位。根据IGS提供的广播星历求解北斗系统各颗卫星的位置,其星下点轨迹如图1所示。以某地(28°N, 113°E)为例,仿真分析2015年5月3日全天北斗区域系统各颗卫星的高度角和俯仰角变化,其卫星星空图如图2所示。

图1　北斗区域系统混合星座的星下点轨迹图

图2　某地北斗区域系统的卫星星空图

从图1中分析,北斗区域系统混合星座主要覆盖区域为(55°S~55°N,55°E~180°E),而在高纬度和西半球大部分地区分布较少;同时从图2中可以看出我国内陆地区的星空图分布,5颗GEO卫星固定分布在南面星空,IGSO卫星出现在南面星空的时间也较多,而北面星空中卫星分布较少,导致北斗系统呈现不均匀的卫星空间分布。

2.2北斗区域系统PDOP值和PRDOP值分布特点

北斗MEO卫星的回归周期为7天,本文选取2015年5月3日-9日(北斗时487周)作为分析时段,分析GPS和北斗区域系统的PDOP值和PRDOP值分布规律。其中选择IGS提供的事后多系统广播星历求解GPS和北斗区域系统的卫星位置,时间统一换算到UTC时,相对定位采用零基线模型。文献[8]指出式(8)中的测量误差应该为用户等价测距误差(UERE),而不是文献[2]和[6]中采用的用户测距误差(URE),选用广播星历中的用户距离精度(URA)来进行权系数的计算,URA定义为UERE的均方差。设置时间间隔为5 min,经纬度间隔取1°×1°,计算GPS和北斗区域系统在区域(55°S~55°N,55°E~180°E)内的PDOP值和PRDOP值,统计7天内计算值95%置信度的均值,结果如图3～图6所示。结果分析如下：

1) 图3和图4中可以分析,GPS在该区域内的PDOP值和PRDOP值分布比较均匀,而且变化幅度小;我国全境GPS的PDOP值分布区间为[1.6,2.2],PRDOP值的分布区间为[1.0,1.6]。

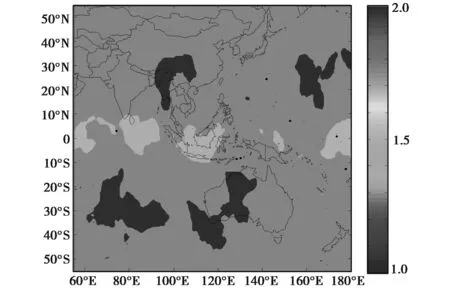
图3　服务区域内GPS PDOP值分布

2) 图4和图5可以得出,北斗系统在服务区域内的PDOP值和PRDOP值分布具有明显的区域特征,变化幅度大,且呈现以赤道为对称轴的南北对称分布。我国除西北和东北以外的地区北斗系统的PDOP值分布区间为[1.4,2.4],PRDOP值分布区间为[1.5,2.1],但是在边缘地带,北斗系统的PDOP值和PRDOP都迅速增大,甚至出现无法定位的情况。

3) 对比图3和图5分析,北斗系统PDOP值在我国除东北和西北以外的其他区域与GPS的PDOP值相差较小,在靠近赤道的部分地区,其值与GPS相当;图4和图6对比分析,我国只有南方地区的PRDOP值在2以内,其他地区与GPS的PRDOP值相差较大。

图4　服务区域内GPS PRDOP值分布

图5　服务区域内北斗系统PDOP值分布

图6　服务区域内北斗系统PRDOP值分布

3北斗系统PDOP值与PRDOP值的一致性分析

目前,在工程应用中通常只采用DOP值预报和分析某地的卫星空间分布和定位精度。文献[9]研究了DOP值进行GPS相对定位预报的适用性,得出非共视卫星增加时,DOP值的预报偏差增大;从图3～图6的对比中,也可以看出PDOP值与PRDOP值存在不一致的情况。

3.1　PDOP值与PRDOP值的数学关系

由基本原理可以得出,单点定位和相对定位中观测方程的系数矩阵有如下关系为

(13)

式中: A为方向向量矩阵; I和E为全1矩阵和单位矩阵,可以得到GPS中DOP值和RDOP值的数学关系[3-4]为

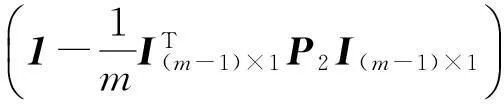
RDOP≤DOP，

(14)

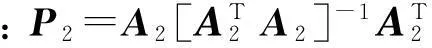
(15)

3.2　仿真实验和结果分析

以某地(28°N, 113°E)为例,仿真分析GPS和北斗区域系统在2015年5月3日的PDOP值和PRODP值,时间间隔为30s,截止高度角为10°,得到结果如表1所示。

实验结果中,北斗系统PDOP值的均值大于GPS的PDOP值,但在约占13%的时间内,其单历元的PDOP值要小于GPS单历元的PDOP值,表明这些时刻内北斗系统的空间位置精度要优于GPS.同时GPS和北斗系统PDOP值与PRDOP值的差值都大于零,可以验证式(13)的正确性,GPS两类精度因子的差值要略大于北斗系统的差值。

表1　 GPS和北斗系统的PDOP值、PRODP值及其差值的正态分布统计

图7　某地2015年5月3日GPS和北斗系统的PDOP值和PRODP值变化

分析影响两类精度因子一致性关系的因素,统计其可见卫星数目和相对定位基准卫星的变化,实验结果如图8～图9所示。从图中分析,PDOP值和PRDOP值的变化都与可见卫星数目的变化有关,卫星数目增加时其值变小,但是PRDOP值的变化还与相对定位的基准卫星选择有关,基准卫星的变化会引起PRDOP值的突变,是造成两类精度因子值不一致的因素之一。同时北斗系统的可见卫星数目在约77%时间内大于或等于GPS的可见卫星数目,但是其精度因子值要大于GPS,这与北斗系统卫星空间分布不均匀有关。

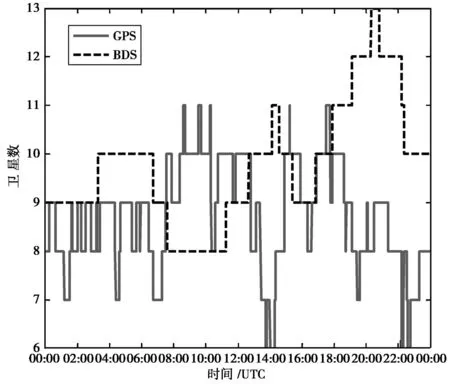
图8　北斗系统和GPS可见卫星数目变化

图9　北斗系统和GPS相对定位基准卫星变化

两类精度因子值的一致性还与相对定位的基线长度和基线方向有关[10],统计以1 km、10 km、50 km和100 km基线长度在8个水平方向两类精度因子差值的均值如表2所示。

表中可以看出,在短基线(小于10 km)中,不同方向两类精度因子差值变化较小;而在中长基线(大于10 km)中,北斗系统不同基线方向的变化不同,该地在东南方向的一致性差值变小,而在西北方向变大,但是在GPS中随着基线长度的增加,各个方向上的一致性差值均变小。实验结果表明在中长基线的相对定位中,北斗系统应选择RDOP值进行不同基线方向的预报和分析。

表2　北斗系统和GPS不同基线长度和方向两类精度因子差值的均值统计

4结束语

从本文的理论推导和仿真实验分析可以得出如下结论:

1) 北斗区域系统在(55°S~55°N,55°E~180°E)区域内的DOP值和RDOP值分布具有明显的区域特征,其PDOP值在我国除东北和西北以外的其他区域与GPS的PDOP值相差较小,而PRDOP值只有在我国南方地区与GPS的PRDOP值比较接近。

2) 北斗系统中DOP值和RDOP值一致性关系与可见卫星数目、基准卫星变化、基线长度和基线方向有关,特别在处理中长基线相对定位时应该使用RDOP值进行不同基线方向的预报和分析。

参考文献

[1] 谢钢.GPS原理与接收机设计[M]. 北京:电子工业出版社,2009.

[2] 杨元喜,李金龙,王爱兵,等.北斗区域卫星导航系统基本定位性能初步评估[J].中国科学, 2014,44(1):72-81.

[3] NIELSEN R O. Relationship between dilution of precision for point positioning and for relative positioning with GPS[J]. TEEE Trans Aerospace and Electronics Systems, 1997，33(1):333-338.

[4] TEUNISSEN P J G. A proof of Nielsen’s conjecture on the GPS dilution of precision[J]. TEEE Trans Aerospace and Electronics Systems, 1998,34(2):693-695.

[5] SHIHAB R H, TABASSUM A. Comparison of DOP of GPS and Galileo in the south asian region[J]. International Conference on Electrical Engineering and Information & Communication Technology, 2014.

[6] 王梦丽,孙广富,王飞雪,等. 混合星座导航系统的加权几何精度因子分析[J].中国空间科学技术, 2007, 10(5):50-56.

[7] 中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件公开服务信号(2.0 版)[R]. 2013.

[8] 杨元喜.卫星导航的不确定性、不确定度与精度若干注记[J].测绘学报, 2012,41(5):646-650.

[9] 曹新运,王坚,刘超.DOP值进行GNSS相对定位预报的适用性研究[J].大地测量与地球动力学, 2013, 33(1):81-85.

[10]王军,张华海.卫星几何分布对GPS相对定位精度的影响[J].测绘科学, 2004,29(2):53-54.

陈正坤(1991-),男,湖南益阳人,硕士生,主要研究方向为卫星导航高精度信息处理技术。

刘文祥(1981-),男,江西宜春人,讲师,主要研究方向为卫星导航信息处理技术。

苏映雪(1983-),女,河北沧州人,讲师,主要研究方向为卫星导航信息处理、系统仿真技术等。

王飞雪(1971-),男,福建长汀人,教授,主要研究方向包括卫星导航定位系统及应用、电子系统抗干扰、扩频信号处理、全数字接收机等。

Analysis for The Effect of DOP and RDOP with BDS

Mixed Constellation

CHEN Zhengkun,LIU Wenxiang,SU Yingxue,WANG Feixue

(SatelliteNavigationandPositioningR&DCenter,SchoolofElectronicScienceand

Engineering,NationalUniversityofDefenseTechnology,Changsha410073,China)

Key words: BDS; mixed constellation; DOP; RDOP