综合指数法在神木气田储层非均质性应用
2016-01-11何文祥
黄 澧, 何文祥
(长江大学 地球环境与水资源学院 教育部油气资源与勘探技术重点实验室, 湖北 武汉 430100)
综合指数法在神木气田储层非均质性应用
黄澧, 何文祥*
(长江大学 地球环境与水资源学院 教育部油气资源与勘探技术重点实验室, 湖北 武汉430100)
摘要:神木气田是典型的致密气藏,储层受成岩期后期作用被致密化,渗透率值普遍较低,用传统的非均质性研究方法来表征有所局限.为定量探讨研究区域储层的非均质性程度,本文采用了综合指数法来进行表征.综合指数法选取的非均质性参数有:渗透率、孔隙度、含气饱和度、泥质含量、含砂量、夹层密度、孔喉半径等.考虑到该区域储层较为致密,故针对开发效果选取了上述前四个参数作为主要参考指标.通过借鉴前人的两种计算各参数权重值的方法来相互印证.结果显示:两种权重计算方法均显示各小层非均质性很强,且太1段最强,符合对该区域太1段地质背景的认识,也反映出沉积背景对储层非均质性起到了控制作用.
关键词:神木气田; 致密气; 综合指数法; 储层非均质性
0引言
国际上关于储层非均质性早在20世纪70年代提出,至今国内外学者已提出了不同的划分方案.例如,Pettijohn(1973年)曾将河流沉积储层划分为5个层次[1];Weber(1986年)不仅考虑到储层的规模,还考虑了非均质性对流体渗流的影响,将储层非均质性分为7类[1];国内具有代表性的分类方案是裘亦楠(1997年)将储层非均质性与开发生产相结合而提出的新分类方案[2].
在这40余年里,国内外学者一直致力于储层非均质性定量表征研究.如模糊数学分析[3,4]、变差函数分析[5]、分型模型分析[6]、地质建模三维模型分析[7-9]、洛伦兹统计分析[10,11]、灰色理论分析[12,13]、熵权值分析[14,15]、新参数分析[16,17]、综合指数分析[18,19]等.
传统方法在评价层间层内非均质性时认为,渗透率是其主要影响参数,应从变异系数、突进系数、级差等来表征储层的非均质性特征.在一般性储层中,这一表征方法足以满足需要.然而,在特殊储层中(如致密储层),仅能从某一角度或某一方面来描述储层的非均质性,可能与实际的情况有所出入.在致密储层中,渗透率普遍较低,离散程度相对于高孔高渗的储层较低,在非均质性评价时,本来非均质性较强的致密储层相反地得出了非均质性较弱的结论.因此,评价这些储层时,不能主要靠渗透率或者某一个参数来表征,而选用多个评价参数来综合评价储层非均质性,更具有实际意义.
1神木气田地质背景介绍
神木气田位于鄂尔多斯盆地伊陕斜坡东北部,如图1所示.西邻榆林气田,南抵米脂气田.神木地区古生界地层缺失中上奥陶统、志留系、泥盆系及下石炭统地层.上、下古生界地层呈平行不整合接触,顶部与中生界地层整合接触.上古生界地层以海陆过渡相——内陆湖盆沉积为主.该区域在太原组时期,海平面上升,沉积模式为潮控三角洲及碳酸盐岩潮坪相沉积;而进入山西组时期,发生海退,沉积模式为河控三角洲,主要发育三角洲平原亚相.如此复杂的沉积背景,反映出了储层非均质性很强.又因为成岩作用影响,导致储层致密化程度严重,加剧了储层的非均质性程度.
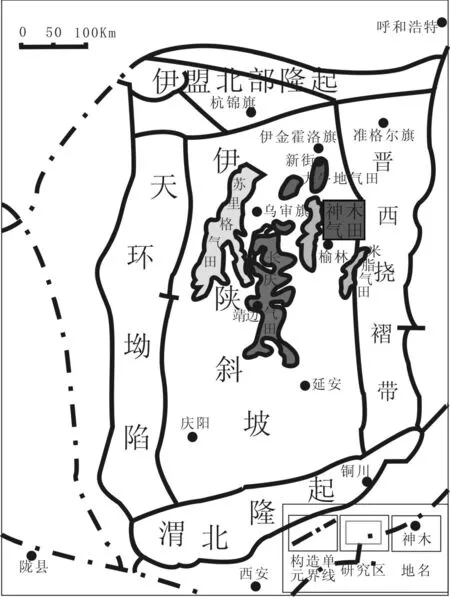
图1 神木气田构造位置
2储层层内非均质性
2.1传统渗透率参数表征
传统渗透率表征参数有:渗透率变异系数(Vk)、突进系数(Tk)、级差(Jk).在无特殊地质条件下的储层中,用来表征储层层内非均质性.
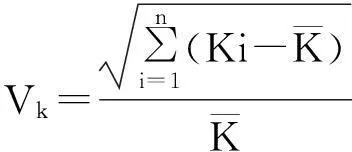
(1)
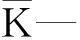
对研究区域各小层进行了研究,其结果如表1所示.
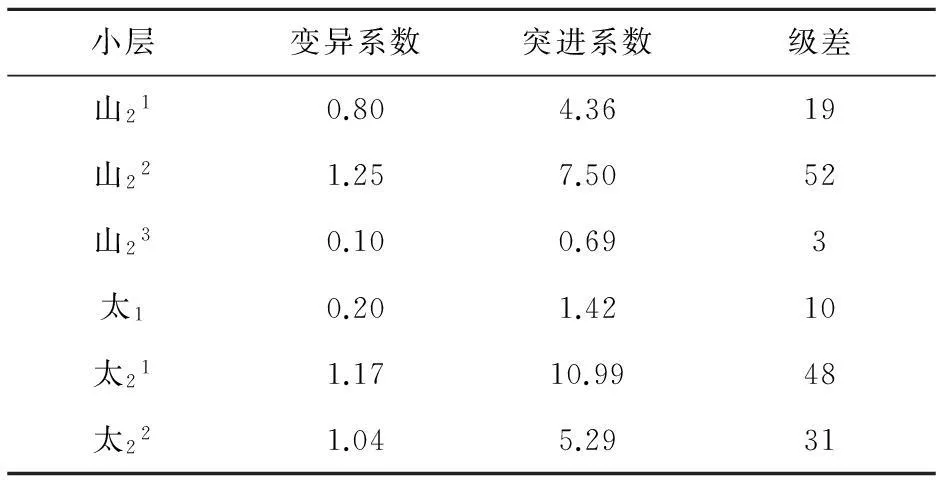
表1 神木气田各小层非均质系数
按传统的评价标准来看,变异系数>0.7、突进系数>3评价为强非均质性,然而由于级差没有定量的评价标准,因此无法准确衡量非均质性程度.在本区,各小层级差均低于60,甚至山23小层级差为3,若用级差评价,层间的非均质性不可能很强.从表1整体上看,山22小层非均质性最强,太1小层非均质性最弱.该结论显示与地质背景的认识不相符.
为了更好地认识该区域储层非均质性,并能够进行定量评价,在此借鉴前人采用综合指数来评价非均质性的方法原理.
2.2综合参数表征方法
目前,常用的非均质参数主要有:渗透率变异系数、突进系数、级差、孔隙度、泥质含量、含气饱和度、砂层厚度、分层系数、砂岩密度、夹层频数、夹层密度,以及有效砂层系数等.综合这些系数,通过各项系数对非均质性影响的权重相加,就会得到新的参数来定量描述研究区域储层非均质性.
考虑到研究区域处于开发早期阶段,基础性地质研究还不透彻,初步提出了影响较大的四种参数(孔隙度、渗透率、含气饱和度、泥质含量)来对储层进行综合评价.
2.2.1非均质性综合参数原理
设非均质综合指数为P,则P在(0,1) 之间变化,P值越小,表示储层的非均质性越强[20].
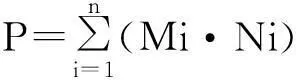
(2)
式(2)中:Mi-第i个参数的权重;Ni-第个i参数标准化值.Ni在实际计算中,由于各个参数的单位不统一,大小相差悬殊,故首先对参数进行归一化处理.最简单的方法是,将各个参数的值统一标定到0~1之间,0代表非储层,1代表高质量储层.
对于值愈大,反映储层性质愈好的参数(如,孔隙度、渗透率等) 的标准化公式为
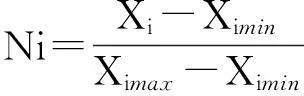
(3)
对于值愈小,反映储层性质愈好的参数(如,泥质含量) 的标准化公式为
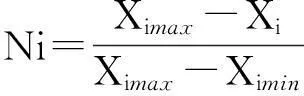
(4)
式(3)和(4)中:Xi-第i个储层参数值;Ximax-第i个储层参数的最大值;Ximin-第i个储层参数的最小值.
2.2.2确定权重
共有两种算法.
(1)变异系数法
参数的权重(Mi)反映该参数的重要程度.求取储层非均质综合指数的目的是确定层间层内平面差异,用不同参数变异系数占整体变异系数的比例来求取.
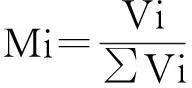
(5)
式(5)中:Mi-第i个参数的权重系数;Vi-第i个参数的变异系数.
(2)熵权法[14]
熵权法原理是把评价中各个待评价单元的信息进行量化与综合后的方法.采用熵权法对各因子赋权,可以简化评价过程.因此,可采用熵值法对指标的权值进行确定.
有n口井m个评价指标,可以得到一个n×m的原始矩阵:A=(aij)n×m

(6)
式(6)中:aij表示第i口井中第j个指标的评价值.
归一化指标值,得到矩阵B
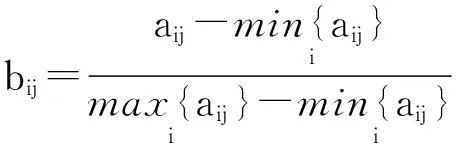
(7)
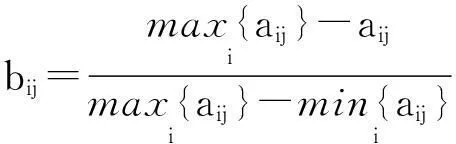
(8)
式(7)表示参数的值越大,对应表征储层非均质性越弱的参数,如孔隙度、渗透率、含气饱和度等;式(8)表示参数的值越大,对应表征储层非均质性越强的参数,如泥质含量.将其数据归一化后得到的矩阵为:

(9)
计算第i口井第j个指标下的评价值的比重,其计算公式如下:
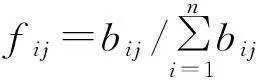
(10)
当fij=0时,令fij=Infij=0
利用熵权法确定各指标的权重.为确定各指标的权重,先计算各指标的熵值,第j个指标的熵定义为:
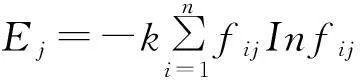
(11)
式(11)中:k=1/Inn
计算第j个指标的熵权Mj
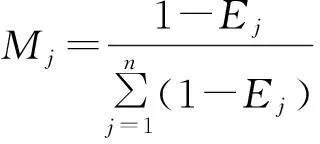
(12)
对不同的小层采用变异权重(权重值1)与熵权(权重值2)等两种类型评价方法进行评价,其结果如表2~3所示.
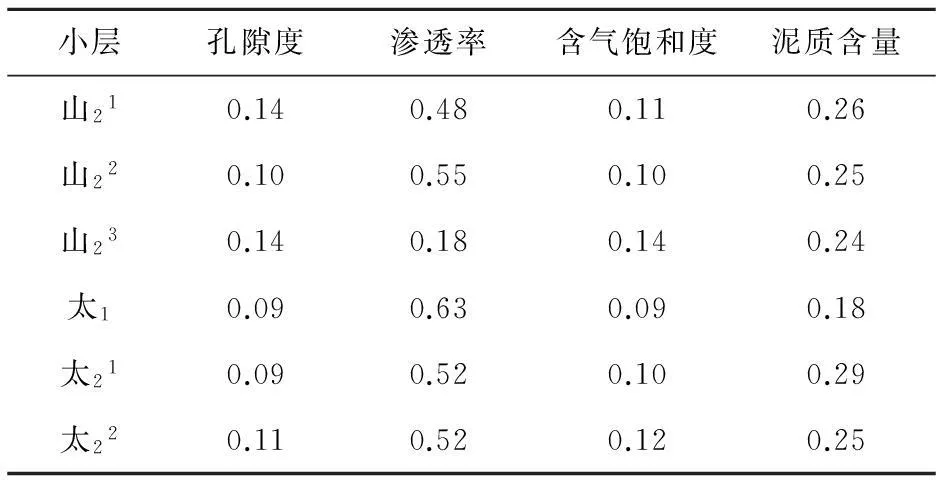
表2 神木气田层内非均质性变异系数法权重值
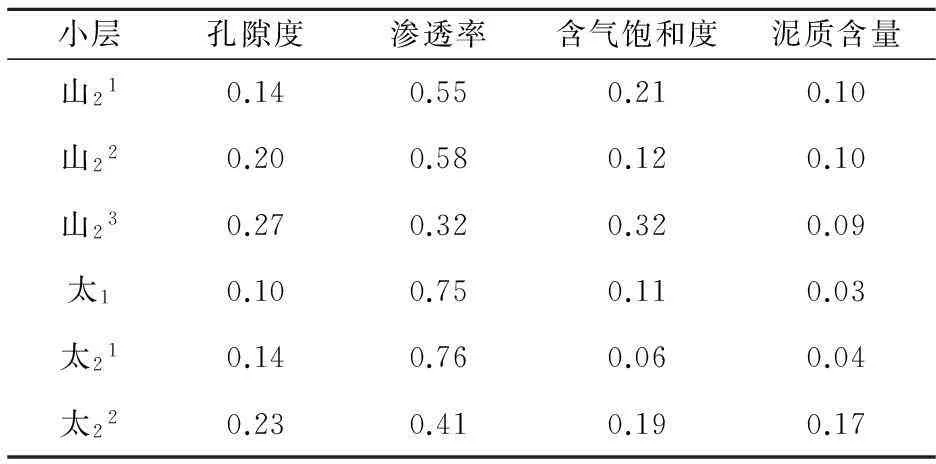
表3 神木气田层内非均质性熵权法权重值
总体来看,渗透率两种权重值在0.48以上,说明渗透率仍然是主要的影响因素.而部分层位因为其它因素的影响,泥质含量变异权重可能达到0.29,含气饱和度的熵权达到0.32.这些数据表明,在影响致密储层的非均质性程度方面,局部区域除渗透率参数作为主要影响因子外,其它的影响因素(如,含气饱和度、泥质含量)亦可能起到关键的作用.
在定量评价非均质性程度方面,除了选取合适的参数以外,还需要建立合适的评价标准,如表4所示.评价标准的建立具有主观性,参考前人各类评价标准[20],将0.3、0.55、0.7设置为不同非均质性程度的界限值.

表4 储层非均质性定量评价标准
注:据魏钦廉等,2009下限值有修改
根据前文定量表征的参数,通过两种权重计算方式得出两类综合指数,如表5所示.经过对比分析,前者的结论显示,太1小层非均质性最强, 山22与太22小层非均质性最弱.这与后者评价一致,匹配非常好.
由熵权的原理得知,在计算过程中会去同存异,导致太1与太21小层的渗透率权重比例大大加强,在评价太21时,两者结论不一致.而山22小层的差异性,是赋予孔隙度与泥质含量的权重相反的结果,其主要参数渗透率权重相差不大,最后评价值接近界限值,因此造成了误差.
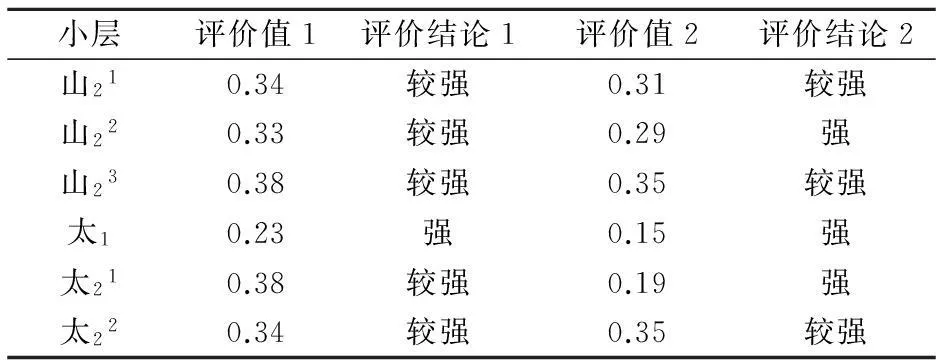
表5 两种不同权重计算评价结论
整体比较来看,两个不同权重计算方法产生的结论较为一致,如图2所示.综合指数在0.15~0.38范围内.与传统方法比较,避免了变异系数、突进系数与级差评价不一致的情况,也综合考虑到了各项参数在地层中的不同权重比例,因而得出的结论具有可靠性.
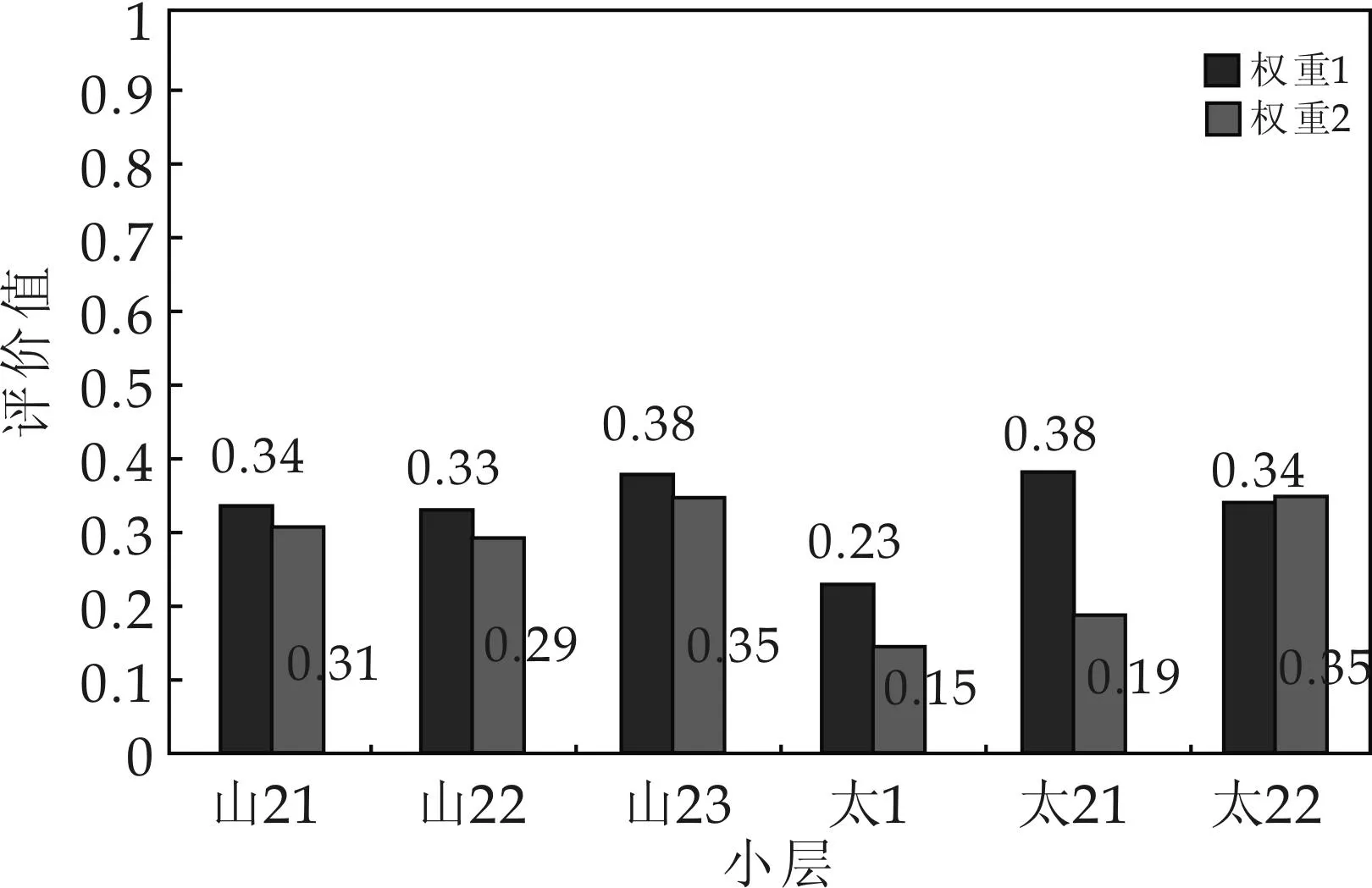
图2 各个小层不同权重评价值柱状图
3储层平面非均质性
储层平面非均质性包括砂体几何形态、各项连续性、孔渗平面变化等.而砂体主要受沉积微相控制.通过计算得到的非均质性综合指数,来绘制平面等值线图,如图3所示,可以刻画其平面上的非均质性程度;再通过小层微相来进行对比,如图4所示,可以验证综合指数在平面上刻画的非均质性是否准确可靠.
以太1小层为例,采用熵权值计算的综合值来进行对比分析.将图3与图4进行对比来看:研究区域的非均质性程度在0.2以下,整体的非均质性程度很强;但分流河道主体部位非均质性值大于0.2,且在分流河道交叉口和分流河道中心部位出
现了非均质性综合指数大于0.3区域.因此,研究区域整体上非均质性很强,其河道砂体局部发育非均质性相对较弱的“甜点”区域适合开发,如A15井、A27井、A26井均获得了较高日产气流.
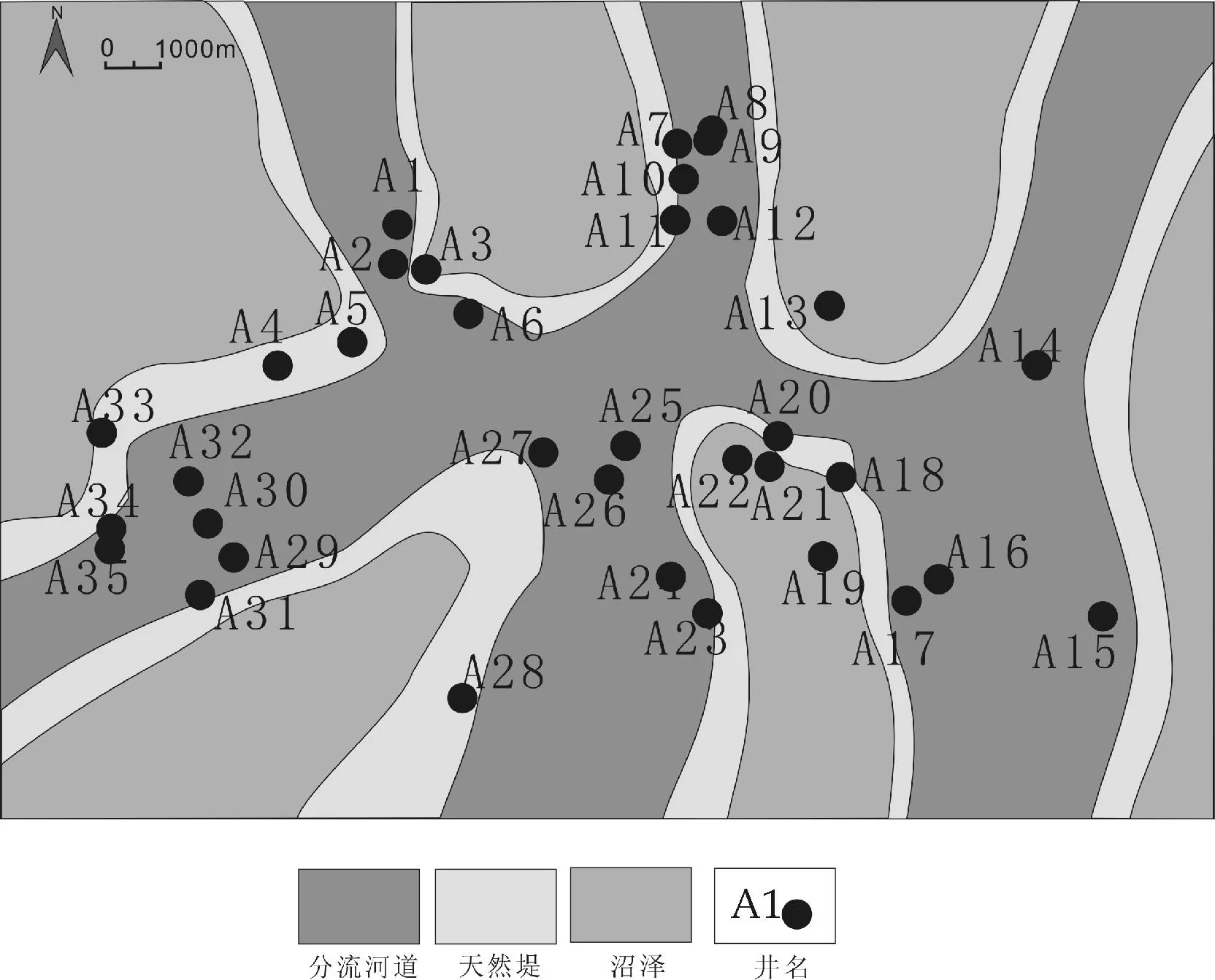
图4 太1小层沉积微相图
4总结
(1)采用传统储层非均质性评价方法,其结论显示:研究区域各小层具有较强的非均质性,而山22小层的非均质性最强;而借鉴前人采用综合方法来分析,得出结论是太1小层非均质最强.后者更符合对该地区的地质认识.
(2)通过两种不同的权重值计算方法,基本结论相似,而部分迥异.这是由于熵权计算法去同存异的特点,使得太21与山22小层评价结论为强非均质性.这一方法有利于分析物性较差、非均质性较强区域的非均质性程度,这推广到全区或者其他地区都具有借鉴意义.
(3)通过非均质性综合指数平面等值线图与太1小层沉积微相与对比分析:在河道中心部位非均质性程度较低,顺着河道方向砂体发育规模较大,即使有后期成岩作用影响,也无法造成很强的非均质性.从全区来看,开发优选区域仍然应以发育厚砂体沉积环境为主.通过熵权计算法,可进一步优化缩小开发范围,节约勘探开发成本.
参考文献
[1] 吴元燕,吴胜河,蔡正旗.油矿质学[M].3版.北京:石油工业出版社,2005:177-178,180-181.
[2] 裘亦楠,薛淑浩.油气储层评价技术[M].修订版.北京:石油工业出版社,1997:224-338.
[3] 杨少春.储层非均质性定量研究的新方法[J].石油大学学报(自然科学版),2000,24(1):53-56.
[4] 朱小燕,孙卫,李建霆,等.陇东城壕——南梁地区长6储层特征研究[J].天然气地球科学,2007,18(6):903-907.
[5] 刘泽容,信荃麟,王伟锋,等.油藏描述原理与方法技术[M].北京:石油工业出版社,1993:56-63.
[6] 杨庆红,谭吕,蔡建超,等.储层微观非均质性定量表征的分形模型[J].地球物理学进展,2012,27(2):603-609.
[7] 张团峰.在储层建模中利用多点地质统计学整合地质概念模型及其解释[J].地学前缘,2008,15(1):26-35.
[8] 吴星宝,李少华,尹艳树,等.相控随机建模技术在非均质性研究中的应用[J].断块油气田,2009,16(2):58-60.
[9] 杨少春,王瑞丽.不同开发时期砂岩油藏储层非均质三维模型特征[J].石油与天然气地质,2006,27(5):652-659.
[10] 刘超,马奎前,李红英,等.基于洛伦兹曲线法定量表征储层非均质性方法的改进与应用[J].中国海上油气,2012,24(2):36-38.
[11] 马玉玲.劳伦兹方法在储层非均质评价中的应用[J].长江大学学报(自科版),2013,10(10):90-91.
[12] 施冬,张春生,许静.储层非均质性灰色综合GIS评价研究[J].物探化探计算技术,2009,31(1):48-52.
[13] 刘吉余,彭志春,郭晓博.灰色关联分析法在储层评价中的应用——以大庆萨尔图油田北二区为例[J].油气地质与采收率,2005,12(2):13-15,82.
[14] 杨少春,杨兆林,胡红波.熵权非均质综合指数算法及其应用[J].石油大学学报(自然科学版),2004,28(1):18-21.
[15] 杨争光,汤军,张云鹏,等.熵权法储层非均质定量评价方法研究——以鄂尔多斯盆地下寺湾长8储层为例[J].地质学刊,2012,36(4):373-378.
[16] 李祖兵,颜其彬,罗明高,等.非均质综合指数法在砂砾岩储层非均质性研究中的应用——以双河油田V下油组为例[J].地质科技情报,2007,26(6):83-87.
[17] 邵先杰.储层渗透率非均质性表征新参数——渗透率参差系数计算方法及意义[J].石油实验地质,2010,32(4):397-399.
[18] 杨少春,周建林.胜坨油田二区高含水期三角洲储层非均质特征[J].石油大学学报(自然科学版),2001,25(1):37-41.
[19] 冯建伟,戴俊生,杨少春,等.综合指数法在河流相储层非均质性研究中的应用——以胜坨油田二区沙二段34储层为例[J].沉积与特提斯地质,2011,31(2):75-81.
[20] 魏钦廉,郑荣才,肖玲,等.阿尔及利亚438b区块三叠系SerieIn feriere段储层平面非均质性研究[J].岩性油气藏,2009,21(2):24-28.
Application of the composite index method to the
heterogeneity of reservoirs in Shenmu gas field
HUANG Li, HE Wen-xiang*
(College of Earth Environment and Water Resources, Key Laboratory of Exploration Technologies for Oil and Gas Resources, Ministry of Education, Yangtze University, Wuhan 430100, China)
Abstract:Shenmu gas field is the typical tight gas reservoirs.The reservoir is densified in the later diagenesis, leading to the general lower value of permeability.So there would be some limitation to use the traditional heterogeneity methods for characterization.In order to quantitatively investigate the reservoir heterogeneity degree of the study area,this method of comprehensive index is used to characterize.The parameters using in this method are many, such as permeability,porosity,gas saturation,clay content, sand content, mezzanine density,pore throat radius.Considering the reservoir densified in this area,the first four main parameters are selected for the development efforts.Two methods of weight are used for reference to confirm mutually.Conclusions is that the two methods showed that the heterogeneity of the small layer is very strong, and small layer of Tai 1 is the strongest, fitting the cognition of the Tai 1 layer geological background.Also reflecting the controlling of deposition background on reservoir heterogeneity.
Key words:Shenmu gas field; tight gas reservoir; composite index method; heterogeneity of reservoirs
中图分类号:TE12
文献标志码:A
文章编号:1000-5811(2015)01-0108-05
通讯作者:何文祥(1968-),男,湖北天门人,教授,博士,研究方向:油藏描述及油气地球化学,hwx@yangtzeu.edu.cn
作者简介:黄澧(1989-),男,湖北荆州人,在读硕士研究生,研究方向:油气储层地质
基金项目:国家自然科学基金青年项目(40902043)
