蜗壳不同心度对核主泵瞬态水动力特性研究

2016-01-11王鹏,袁寿其,王秀礼等

振动与冲击 2015年22期

蜗壳不同心度对核主泵瞬态水动力特性研究

王鹏，袁寿其，王秀礼, 周帮伦，卢加兴

(江苏大学国家水泵工程技术研究中心，江苏镇江212013)

摘要：为研究核主泵在不同工况下运行的瞬态特性，基于RNG k-ε模型采用CFX三维非定常数值模拟方法分析其在4种不同同心度下压力脉动变化规律。结果表明，改变偏心距并未改变叶轮主频，随偏心距增加叶轮内压力脉动幅值先减小后增大。各偏心距在不同工况下压力呈相似规律变化，且波动次数等于导叶数目，即叶轮内流动状态受导叶影响较大。小流量工况下脉动幅值随偏心距增加波峰出现位置逐渐向下一时刻推移，且不同偏心距下压力脉动幅值差别较大；设计工况下叶轮流道内压力脉动幅值波动明显小于小流量工况，出口压力脉动幅值远大于进口。大流量工况时叶轮内各监测点压力脉动幅值在各偏心距下从叶轮进口到出口均呈不稳定波动，波动幅值远大于设计工况。偏心距为10～15 mm时核主泵运行压力脉动最小。

关键词：核主泵；压力脉动；偏心距；数值模拟

中图分类号:Th111文献标志码：A

基金项目：国家自然科学基金资助项目(61403212);天津市应用基础与前沿技术研究计划资助项目(14JCQNJC04600)

收稿日期：2014-08-18修改稿收到日期：2014-10-11

Volute eccentricity effect on transient dynamic characteristics of nuclear main pump

WANGPeng,YUANShou-qi,WANGXiu-li,ZHOUBang-lun,LUJia-xing(National Research Center of Pumps, Jiangsu University, Zhenjiang 212013, China)

Abstract:In order to study the transient dynamic characteristics of a nuclear main pump under different conditions,the pressure fluctuation under four different volute eccentricities were analyzed based on the RNG k-ε model by using CFX three-dimensional unsteady numerical simulation methods. The results show that the change of eccentricity does not alter the dominant frequency of impeller, however, with the increasing of eccentricity, the pressure amplitude inside the impeller decreases first and then increases. The pressure has a similar changing trend for different eccentricities under different working conditions and the wave frequency is just equal to the number of guide vanes which indicates that the flow state inside the impeller is greatly influencd by guide vanes. Under small flow conditions, with the increase of eccentricity the peak of pressure fluctuation amplitude gradually delays to appear and the amplitude difference of the pressure fluctuation becomes larger under different eccentricities. Under the design working conditions, the fluctuation in the impeller flow passage is less than that under small flow conditions and the pressure amplitude at outlet is greater than at inlet. Under large flow rates, at monitor points, the pressure amplitudes within the impeller under different eccentricities from inlet to outlet are unstable, and the fluctuation amplitudes are greater than under the design conditions.The analysis results show that the pressure fluctuation of nuclear main pump under various operating conditions reaches its minimal when the eccentricity is within 10～15 mm.

Key words:nuclear main pump; pressure fluctuation; eccentricity; numerical simulation

反应堆冷却剂主循环泵简称核主泵，作为核电站一回路系统中唯一旋转设备，长期稳定运行对整个核电站安全作用至关重要。压力脉动为引起核主泵机组振动噪声及不稳定流动的重要因素之一，也是判断核主泵水力设计好坏的依据之一。泵内部流场瞬态特性研究可采用试验及数值模拟方法。王福军等[1-2]对双吸离心泵吸水室及压水室内压力脉动特性进行研究表明，双吸离心泵中叶轮与隔舌区动静干涉为引起压力脉动的主要因素。刘厚林等[3]提出叶片出口宽度对离心泵瞬态不稳定流动特性有一定影响，模型泵噪声信号随叶片出口宽度增加轴频峰值变化规律复杂。Hodkiewicz等[4]试验发现双吸离心泵产生瞬态不稳定流动的主因为吸水室内存在不同尺度漩涡。González等[5]研究表明，在偏向大流量工况下由于泵内部不稳定流动致使吸水室内流场速度分布不均进而引起叶轮进口不稳定流动。袁寿其等[6-7]通过对不同类型的泵数值模拟表明，偏工况下运行也会造成瞬态不稳定流动。为探究汽蚀工况下不稳定流动，王秀礼等[8]分析由无汽蚀到严重汽蚀时离心泵内部瞬态流动。文献[9]则采用阶梯隔舌方法探究离心泵动静干涉作用。文献[10]采用复合叶轮方法研究核主泵内部压力脉动特性。王春林等[11]通过研究核主泵非定常流场中瞬态特性，获得核主泵内部压力脉动变化规律。

至今，对怎样减小核主泵瞬态不稳定流动的研究仍不深入，相关文献亦较少见。因不稳定流动主要源自转子、定子间动静干涉，为此本文在保持泵体、叶轮、导叶等几何参数不变情况下，利用偏移泵体重心方法研究重心偏移后导叶与蜗壳相对位置变化对叶轮内压力脉动特征与流量间关系及压力脉动分布规律，探究核主泵瞬态水动力特性。

1研究对象及偏移方法

1.1研究对象及计算模型

以自主研发的AP1000模型泵为研究对象，其主要性能参为：流量Q=17 886 m3/h、扬程H=111.3 m、转速1 450 r/min、比转速344，叶轮结构形式为混流式。为满足水力性能好、强度高、易加工及探伤要求，蜗壳设计成环形。据要求叶片为5叶，导叶数11。采用PRO/E软件生成三维计算区域模型，整个计算区域由进口段、叶轮、导叶、蜗壳及出水段组成，见图1。

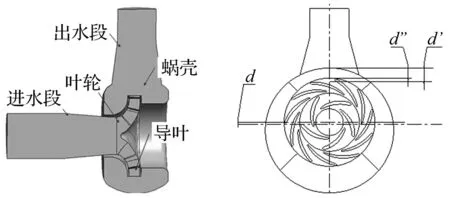
图1 三维造型及计算区域Fig.13DmodelsandComputationaldomain图2 偏心示意图Fig.2Thedisplacementsschematicdiagram

1.2重心偏移方法

由图1三维模型知，出水段存在使整个泵体为非对称结构，进而使核主泵内部出现非定常流动现象，如失速、汽蚀、回流等。为使泵体对称，在保证叶轮及导叶中心轴线不变情况下将蜗壳及出水段重心向出水段方向分别偏移5 mm、10 mm、15 mm及20 mm。偏移后导叶与蜗壳隔舌位置由偏移前d’变为d’’，偏移示意图见图2。

2数值模拟

2.1网格划分及无关性验证

采用CFX前处理网格划分软件ICEM-CFD划分网格，整个计算区域均用六面体结构网格，计算区域包括进口水段、叶轮、蜗壳、导叶及出水段。计算区域及网格划分见图3。

图3　计算区域及网格 Fig.3 Calculation domain and structure mesh

网格无关性检查可通过改变网格尺度实现，计算中逐步减少网格尺度。为确定网格数及疏密程度对计算的影响，选6种网格数进行模拟，并给出计算扬程与实际扬程比值H’(无量纲扬程)随网格数变化规律，结果见图4。由图4可知，核主泵无量纲扬程随网格数增加而增加，网格数增加到550万以上时扬程变化趋小。而网格数428万与550万时扬程差范围小于5%，为节约计算时间及资源，总网格数取428万。

图4　网格无关性分析 Fig.4 Mesh independence analysis

2.2数值计算方法及边界条件

利用ANSYS CFX 14.5全隐式耦合多网格线性求解器,采用雷诺平均动量方程描述该泵内不可压缩流动。对叶轮机械进行稳态计算时，由于标准的RNGk-ε湍流模型在计算含旋转流动中能较好模拟高应变率，故用该模型及连续性方程使动量方程封闭。叶轮流道内水体为旋转体，导叶及蜗壳内水体为非旋转体，非定常计算的交界面设为TransientRotor-Stator模式,该交界面对两部分水体间动、静干涉有重要作用。为获得最经济的计算时间步长，非定常计算时间步长为叶轮旋转周期的1/120，即每个时间步长内叶轮旋转3°。据核主泵参数，时间步长Δt=3.448 3× 10-4s。

计算域进口采用压力进口条件，出口为给定出口质量流量，通过出口边界条件控制模型的质量流量。速度项、湍动能及湍流粘性系数均采用二阶迎风格式，近壁区用标准壁面函数修正湍流模型，计算收敛精度为10-5。

2.3监测点选取

为监测偏心条件下导叶与蜗壳相对位置改变对核主泵叶轮内部压力随流量的变化规律，在叶轮流道内从叶轮进口边到出口边依次选取监测点IA、IB、IC监测不同流量、不同导叶与蜗壳相对位置叶轮流道内流动状态，见图5。

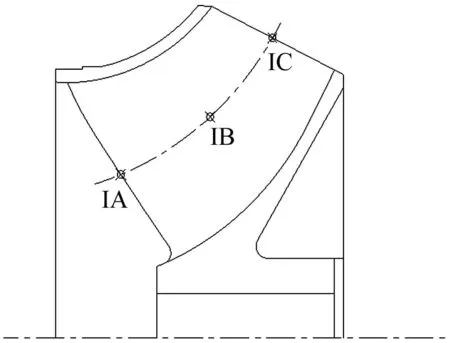
图5　叶轮内各监测点示意图 Fig.5 Scheme of monitors located in the impeller

3计算结果与分析

3.1压力脉动时域分析

设计工况下瞬态压力变化时域图见图6，以3°为采集点对叶轮旋转一周作时域图。图6(a)～(d)分别为0.6Qd～1.2Qd工况不同偏心距时叶轮内各监测点时域变化，由图6看出，不同工况下压力脉动时域特性均呈周期性变化。在一个旋转周期内，各监测点均不同程度波动11次，波动次数恰等于导叶数目，即叶轮内流动状态受导叶影响很大。从进口IA到出口IC各监测点压力变化逐渐增加，进口处偏心距5 mm与15 mm时压差最大，20 mm次之，10 mm最小；一个旋转周期内，第一象限各监测点压力波动较小。处于叶轮中间流道中间IB呈相似规律，但随偏心距增加波峰出现位置逐渐向下一时刻推移。压力在叶轮出口IA处波动最大，此时偏心距为20 mm波峰已推移到偏心距10 mm及15 mm波谷处。而偏心距为15 mm时压力除在初始1/12及1/4周期处出现不稳定外其余均呈稳定变化。对比4种偏心距在叶轮出口处压力波动知，偏心距15 mm时波峰与波谷波幅值最小、最平稳。

分析因未偏心前从叶轮内流出的介质不能平顺与泵体内介质相汇合，而与泵体内介质相撞，从而使流出叶轮介质流速下降与泵体内流速相同，部分动能通过撞击传给泵体内介质使其压力增高。随偏心距进一步增大，使核主泵泵体内介质流速、流出叶轮与导叶流速方向、大小基本一致，从叶轮流出的介质能平顺通过导叶流入泵体，使叶轮周围介质速度、压力分布较均匀。偏心距增大到20 mm时由于重心过度偏移，使从叶轮及导叶流出的流体与泵体存在大量撞击，改变泵体内流体速度从而出现不稳定流动，即波峰及波动幅值呈规律性变化。

图6　不同工况、不同偏心距压力脉动频域图 Fig.6 Pressure fluctuations of different eccentricities under different conditions

3.2压力脉动频域分析

为分析不同工况各偏心距下核主泵瞬态水动力特性，采用快速傅里叶变换(FFT)对各监测点压力信号进行频谱分析。

图7(a)为0.6Qd工况时各偏心距在叶轮进口IA、叶轮中间(IB)及出口处(IC)的频域图。由于设计工况叶轮转速为1 450 r/min，故转频为24.16 Hz，叶频为120.8 Hz。不同偏心距脉动频率均以叶轮转频为主，随偏心距增加脉动幅值先减小后增大。偏心距为5 mm、20 mm时压力脉动幅值较大，10 mm、15 mm时较前者下降19.5%、24.3%。之后幅值由大到小分别出现在2、4、6倍叶频处，20 mm时甚至在8倍频处出现脉动。压力脉动幅值变化规律与进口趋势相同，但每个监测点最大幅值从叶轮进口到出口呈增大趋势，较进口分别增加74.3%、82%。小流量工况下偏心距不同对叶轮内压力脉动影响也不同，因偏心20 mm后导叶与蜗壳隔舌相对位置发生变化(更靠近隔舌)，此时从叶轮内流出的高速流体与出口锥管处类似隔舌处发生动静干涉致压力脉动幅值呈增长趋势。图7(b)为1.0Qd工况时各偏心距在叶轮流道内3监测点IA、IB、IC处频域图。由该图可知，此时压力脉动幅值较偏离工况时小，各偏心距间最大脉动幅值无明显差异，除1倍转频压力脉动变化较明显外，2、4、6倍叶频处也呈一定程度波动；偏心10 mm时在1倍转频处脉动幅值较小且在其余叶频处未见明显波动。叶轮出口处压力脉动强于进口及流道中间点IB，各偏心距在出口处脉动幅值先减小后增大，偏心距为10 mm时最小。

图7(c)为1.2Qd工况时各偏心距在叶轮流道内3监测点IA、IB、IC处频域图。由该图看出，大流量工况下各监测点最大压力脉动幅值均无明显变化，但在2、4、6倍叶频处最大幅值均较设计、小流量工况时大，尤其2倍叶频处最大幅值较设计工况分别大12.5%、8%、4.7%。偏心距为5 mm、20 mm时在8、10倍频处均有一定程度波动。

图7　不同工况、不同偏心距压力脉动频域图 Fig.7 Pressure fluctuations of different eccentricities under different conditions

图8　不同工况下不同偏心距压力脉动频域图 Fig.8 Pressure fluctuations under different eccentricities conditions

图8为各偏心距在各工况时叶轮流道内3监测点IA、IB、IC处频域图。由8(a)看出，偏心距为5 mm时设计工况下脉动幅值最小，偏离工况时脉动幅值较大。偏向小流量工况时尤其叶轮出口处最大脉动幅值较大，但仅2倍叶频处出现脉动其余无波动。小流量时最大脉动幅值较设计工况大13.2%，1.2Qd大8.5%。偏心距从5 mm增加到20 mm时，各工况下最大压力脉动幅值呈相同变化趋势，但偏心距10 mm时最大脉动值却较各偏心距小15%。由此可见，同等条件下偏心距10 mm时核主泵内部压力脉动幅值最小。

图9为核主泵叶轮进口、中间截面及叶轮出口各偏心距在各工况下最大不稳定压力幅值比较。由图9看出，0.6Qd时在叶轮进口处最大幅值先减小后增大，偏心距10 mm时幅值最小约200 kPa，最大幅值出现在偏心距20 mm时，约250 kPa。各偏心距下无论叶轮流道中间位置或出口处，小流量工况下脉动幅值始终最大。1.0Qd工况时，在整个叶轮流道内各监测点处脉动幅值随偏心距增加先减小后增大，偏心距15 mm时最小。1.2Qd工况、偏心距10 mm及15 mm时叶轮出口处脉动幅值较其它偏心方案小，且在10 mm时达最小约7%。原因可能重心偏移过大后导叶出口处液流与蜗壳动静干涉对叶轮内部流场非定常压力脉动掺混结果。由于叶轮进口处远离导叶出口-动静干涉点，进口处受动静干涉程度较小，经能量转化后叶轮出口处动能较大，且受动静干涉影响，故压力脉动幅值变化较大。

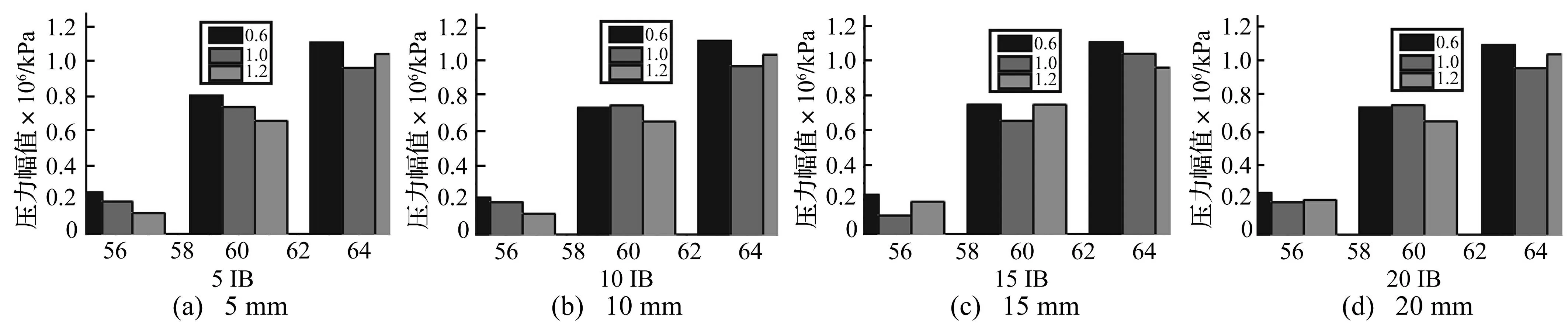
图9　不同工况、不同偏心距最大压力脉动幅值对比 Fig.9 The pressure fluctuationsamplitude comparisonamong different eccentricities conditions

4实验验证

为验证数值模拟的准确性，以清水介质在开式试验台上对核主泵最优偏心距10 mm时进行样机性能试验，试验现场见图10。

图10　模型泵性能测试实验台 Fig.10 The test rig of model pump

图11　泵性能预测与试验对比 Fig.11 Comparison of the predicted and experimental performancecurves of pumps

图11为模型泵扬程、效率计算值与试验值比较。由该图看出，虽小流量时计算扬程、效率误差有明显加大趋势，但整个流量范围内误差在可接受范围，计算值与试验值吻合较好，计算值略高于试验值，设计工况扬程误差不超2%，效率误差不超5%。因此本文所用数值计算方法及三维模型可靠性较高，进行径向力分析具有一定可信度。

5结论

(1)工况改变对各监测点在不同同心度下压力脉动影响大致相同，增加偏心距波峰出现位置逐渐向下个时刻推移；脉动幅值变化随偏心距增加先减小后增大，偏心距为10～15 mm时各监测点在低、高频区最大脉动幅值波动范围较其它偏心方案小。

(2)改变偏心距叶轮主频并未改变，因偏心后导叶与蜗壳隔舌的动静干涉作用，叶轮次主频会受不同程度影响。偏心距10 mm时叶轮流道内各监测点瞬态压力幅值较小。

(3)核主泵数值预测外特性曲线与试验外特性曲线较吻合，说明本研究数值模拟结果及径向力计算模型具有一定准确性。

参考文献

[1]王福军,张玲,张志民．轴流泵不稳定流场的压力脉动特性研究[J]．水利学报,2007,38(8):1003-1009．

WANG Fu-jun, ZHANG Ling, ZHANG Zhi-min．Analysis on pressure fluctuation of unsteady flow in axial flow pump [J]．Journal of Hydraulic Engineering,2007,38(8):1003-1009.

[2]王福军,姚志峰,肖若富,等．双吸离心泵吸水室和压水室压力脉动特性试验研究[J]．水利学报,2012,43(4):473-479.

WANG Fu-jun, YAO Zhi-feng, XIAO Ruo-fu, et al. Experimental investigation on pressure fluctuations in suction chamber and volute of a double suction centrifugal pump[J]. Journal of Hydraulic Engineering,2012,43(4):473-479.

[3]刘厚林,王勇,谈明高,等. 叶片数对离心泵内流诱导振动噪声的影响[J]. 排灌机械工程学报,2012,30(2):131-135.

LIU Hou-lin, WANG Yong,TAN Ming-gao, et al. Effect of number of bladeson flow induced vibration and noise of centrifugal pumps[J]. Journal of Drainage and Irrigation Machinery Engineering, 2012, 30(2): 131-135.

[4]Hodkiewicz M R, Norton M P. The effect of change in flow rate on the vibration of double-suction centrifugal pumps[J]. Journal of Process Mechanical Engineering,2002,216(1):47-58.

[5]González J，Parrondo J，Santolaria C，et al． Steady and unsteady radial forces for a centrifugal pump with impeller to tongue gap variation[J]． Journal of Fluids Engineering，2006，128(3):454-462.

[6]袁寿其,周建佳,袁建平,等．带小叶片螺旋离心泵压力脉动特性分析[J]．农业机械学报,2012,43(3):83-87.

YUAN Shou-qi, ZHOU Jian-jia, YUAN Jian-ping, et al. Characteristic analysis of pressure fluctuation of unsteady flow in screw-type centrifugal pump with small blade [J]．Transactions of the Chinese Society for Agricultural Machinery,2012,43(3):83-87.

[7]施卫东,邹萍萍,张德胜,等．高比转数斜流泵内部非定常压力脉动特性[J]．农业工程学报,2011,27(4):147-152.

SHI Wei-dong,ZOU Ping-ping,ZHANG De-sheng,et al. Unsteady flow pressure fluctuation of high-specific-speed mixed-flow pump[J]．Transactions of the CSAE,2011, 27(4):147-152.

[8]王秀礼,袁寿其,朱荣生,等．离心泵汽蚀非稳定流动特性数值模拟[J]．农业机械学报,2012,43(3):67-72.

WANG Xiu-li, YUAN Shou-qi, ZHU Rong-sheng, et al. Numerical simulation on cavitation unsteady characteristics in centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery,2012,43(3):67-72.

[9]袁寿其,祝磊,袁建平,等.不同型式隔舌离心泵动静干涉作用的数值模拟[J]. 农业工程学报,2011,27(10):50-55.

YUAN Shou-qi, ZHU Lei, YUAN Jian-ping, et al.Numerical simulation for rotor-stator interaction of centrifugal pump with different tongues[J]. Transactions of the Chinese Society of Agricultural Engineering,2011,27(10): 50-55.

[10]王秀礼,袁寿其,朱荣生,等.基于CFD数值模拟的复合叶轮核主泵压力脉动特性研究[J]. 原子能科学技术,2014,48(1)：99-105.

WANG Xiu-li, YUAN Shou-qi, ZHU Rong-sheng, et al. Numerical simulation on pressure fluctuation of reactor coolant pumpwith complex impeller based on CFD technique [J]. Atomic Energy Science and Technology，2014,48(1):99-105.

[11]王春林,易同祥,吴志旺,等．混流式核主泵非定常流场的压力脉动特性分析[J]．动力工程，2009,29(11):1036-1040.

WANG Chun-lin, YI Tong-xiang, WU Zhi-wang, et al. Analysis on pressure fluctuations of unsteady flow field in mixed flow main coolant pump[J]. Journal of Power Engineering,2009,29(11):1036-1040.

[12]龙云,朱荣生,付强,等．核主泵小流量工况下不稳定流动数值模拟[J]．排灌机械工程学报,2014,32(4):290-295.

LONG Yun, ZHU Rong-sheng, FU Qiang, et al．Numerical analysis on unstable flow of reactor coolant pump under small flow rate condition[J]. Journal of Drainage and Irrigation Machinery Engineering,2014,32(4):290-295.

[13]丁剑,刘厚林,王勇,等．叶片出口角影响离心泵噪声辐射数值研究[J]．振动与冲击,2014,33(2):122-127.

DING Jian, LIU Hou-lin, WANG Yong, et al．Numerical study on the effect of blade outlet angle on centrifugal pump noise[J]. Journal of Vibration and Shock,2014,33(2):122-127.