BM3D算法在海洋SAR图像去噪中的应用∗

石 健,汪 洋,黄海风,余安喜,李 威

(1.国防科技大学电子科学与工程学院,湖南长沙410073;2.卫星海洋环境动力学国家重点实验室,浙江杭州310012)

0 引言

可以合理地假设在一个雷达分辨单元内存在大量的散射体,散射体反射天线发射来的电磁波,SAR接收到的信号是这些散射体回波的矢量和。各散射体回波在空间叠加时,会出现交叠区某些地方振动加强,某些地方振动减弱或完全抵消的现象。因此,SAR接收到的总回波有很大的随机起伏,这种起伏在图像上的反映就是相干斑噪声。相干斑的存在使SAR图像灰度变化剧烈,分辨率明显变差,严重影响了SAR图像的后续应用。

目前针对SAR图像噪声滤除主要有多视处理和相干斑滤波两种方法。多视处理改善了图像质量,却极大损失了空间分辨率,破坏图像细节。而滤波方法又分为空间域滤波和变换域滤波[1],前者包括常见的均值滤波、Lee滤波、Frost滤波等,后者的代表是基于小波变换的阈值滤波方法。本文中的三维块匹配(BM3D)算法属于变换域滤波方法。

BM3D算法是一种将非局部思想与变换域方法成功结合的图像去噪算法,是目前去噪效果最好的方法之一[2-3]。相比由相干斑乘性噪声模型发展而来的空域方法,变换域方法如BM3D是基于加性噪声模型的[4]。BM3D算法通过分割图像块,并将相似块匹配分组,后在变换域中去噪,算法性能与图像的相似性有一定关联[5]。将其用于海洋SAR图像去噪,利用了海洋是一种同质较均匀场景的特点,图像分块后相似性较高,能够得到较好的去噪效果。本文通过实验发现参数设定对去噪效果有很大的影响,总结了BM3D算法的参数设定原则,并应用于实测数据的处理中。

1 BM3D算法介绍

相干斑噪声可以认为是一种随机乘性噪声,其数学模型如下：

式中,I表示含有相干斑噪声的SAR图像强度,R表示目标的雷达散射特性(不含噪声),u即为相干斑噪声,它是一个均值为1、方差为σ2u的平稳白噪声。实质上相干斑的滤除就是从原图像I到去噪后图像R的映射。如果在去噪之前对原图像进行对数变换,把乘性噪声变成加性噪声,式(1)变为

此时相干斑近似为独立的零均值加性高斯白噪声,这是运用BM3D算法去噪的前提。

BM3D算法流程如图1所示[6-10]。

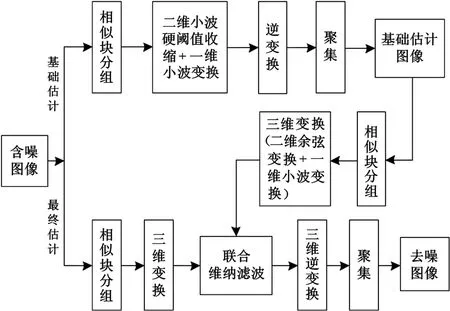
图1 BM3D算法流程

第一步：基础估计,将图像分割成块并逐块估计。

1)分组：构造大小为N1×N1的二维凯撒窗在图像I上按照设定的步长移动搜索取图像块。假定初始选中的块为P,在相似图像块搜索过程中滑窗选中的块为Q,以左上角顶点像元S P、S Q为该块对应的矩阵数值。在设定大小的搜索区域内寻找块间距离较小的相似块,距离D定义为两个块对应的矩阵数值差的模除以块的大小,公式如下：

选取合适的距离阈值τ1,满足D＜τ1的两图像块相似性高,属于同一集合B P,最后将B P中的块矩阵集合按照距离D的大小排列,形成三维矩阵T P。

2)硬阈值收缩：对三维矩阵T P进行二维Bior小波硬阈值收缩和块间径向一维Haar小波变换τ3D,为三维变换滤波后B P中块的估计值集合。利用如下硬阈值估计公式调整变换系数r：

式中,x为集合B P中块的矩阵数值,λ3D为硬阈值收缩的阈值参数,σ为估计的噪声标准差。由于图像的大部分真实信息都集中在三维矩阵较大值处,而噪声往往集中在较小值处,因此通过硬阈值滤波,能够在有效去除噪声的同时保留大部分真实信息。

3)聚集：经过硬阈值收缩后,每个块或每个像元都得到一个估计值,N P表示相似块集合T P经过硬阈值收缩后矩阵数值中非零的个数,则基础估计权值为

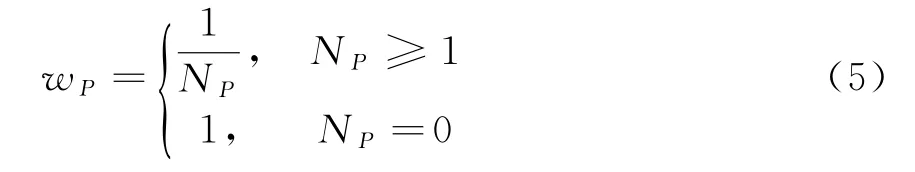
对于某一个像元i,可能会出现在多个块内,需要对这些有重叠的块估计值进行加权平均来得到i的基础估计值,公式如下：

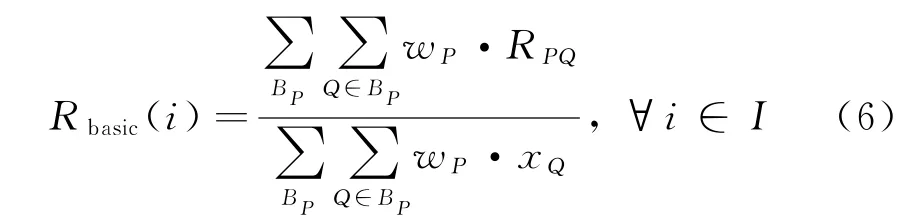
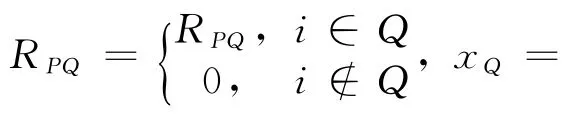
第二步：最终估计,对基础估计后的图像再进行分块并逐块估计。

1)分组：对第一步中得到的基础估计图像Rbasic以类似原则再次进行块匹配,形成新的三维矩阵T P2。此时有两个对应的三维矩阵,一个是第一步得到的由原图像中相似块组成的三维矩阵T P,另一个是由基础估计生成的图像中相似块组成的三维矩阵T P2。

2)联合维纳滤波：对两个三维矩阵均进行三维变换κ3D(二维DCT余弦变换+一维Haar小波变换),以基础估计图像对应的三维矩阵T P2对原图像对应的三维矩阵T P进行维纳滤波,得到最终估计权值为

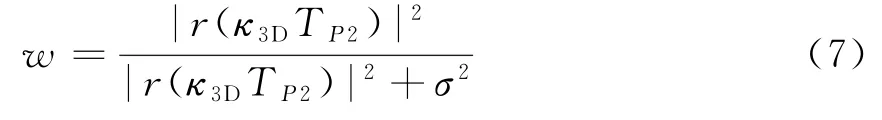
3)聚集：同理,需要对这些块估计值进行加权平均来得到i的最终估计值：

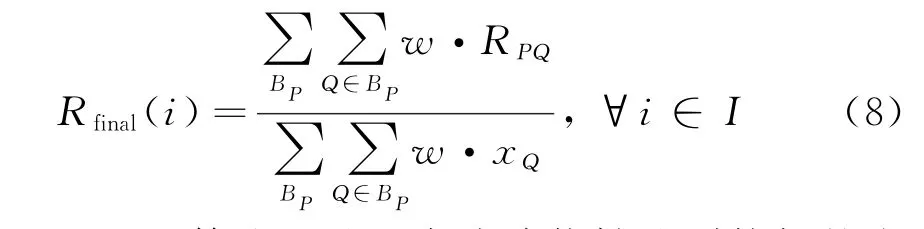
BM3D算法通过两次滤波能够达到较好的去噪效果,但也存在一个问题,即当噪声达到一定程度后,BM3D去噪性能出现较明显的下降趋势,主要原因是噪声变强后相似块匹配的准确性会急剧下降[11]。在理想情况下,不含噪声的图像中块间距离为

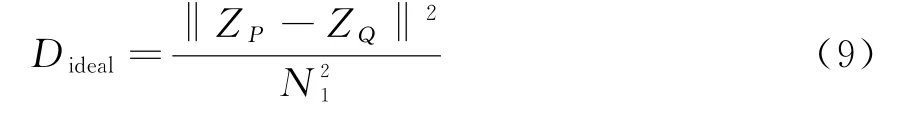
式中,Z P,Z Q为图像块P、Q对应的矩阵数值。由于没有噪声的干扰,可以认为Dideal是一个定值。但在实际情况下,无法获得不含噪的真实图像,则式(3)的块间距离是一个随机变量：

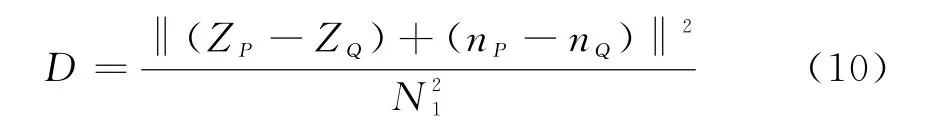
式中,n P,n Q为图像块对应的噪声分量。上式中距离D的均值与方差为

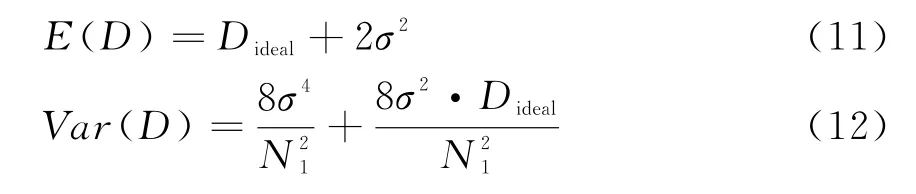
此时方差随着σ的增大而急剧增大,从而对于较大的噪声标准差σ或者较小的窗尺寸N1,不同的距离D的概率密度可能严重重叠,导致错误的块匹配,使得有较大距离的块被判定为相似的。由上述的问题可知,BM3D算法中如噪声标准差、块匹配搜索窗大小等参数对于去噪效果有很大影响,因此研究如何选择相关参数是十分必要的。

2 BM3D算法参数选择

2.1 参数选择原则

BM3D算法需要设定的初始参数有基础估计步骤中的搜索窗尺寸N1、滑动步长Nstep、搜索范围尺寸NS、最大相似块个数Nmax、硬阈值收缩阈值λ3D和块间距离阈值τ1,在最终估计步骤中同样有搜索窗尺寸、滑动步长、搜索范围尺寸、最大相似块个数和块间距离阈值。各参数并不是相互独立的,在设定参数时要综合考虑多种影响,由此总结BM3D算法的参数选择原则[12]：

1)在相似块搜索过程中,搜索窗大小N1×N1决定了图像块的大小,在硬阈值收缩时,需要对小波系数分解,窗尺寸必须为2的幂,即N1=2n。但同时N1过大也不利于图像的去噪,一方面提高了算法的复杂度,增加了运算时间;另一方面,以块内左上角像元P来代表该块,块的尺寸过大,可能会包含一些与P相差较大的像元,导致相似块匹配失真。对于最终估计步骤中的搜索窗,尺寸选取与N1相等或相近,但不需要满足。

2)BM3D算法有两种模式来搜索相似图像块,完全搜索模式下需要搜索全图所有的块,得到的结果精确但是运算量过大;快速搜索模式下在指定区域内搜索相似块,此时要设定搜索范围的尺寸NS,与搜索窗尺寸N1、滑动步长Nstep、最大相似块个数Nmax有关,且BM3D算法要求NS输入值为奇数。假定在一个方形的搜索区域内,要找到至多Nmax个相似块,则边长尺寸NS取值一般满足如下关系：

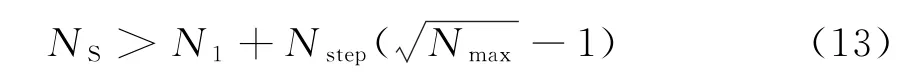
其中为了保证某个像元点会出现在多个相似块内,最终求值时能够加权平均减小估计误差,滑动步长可取值Nstep＜N1/2。

3)在块匹配分组时,相似块组成一个三维数组集合,设定集合中元素的个数最大值为Nmax。Nmax越大,同一类相似块越多,理论上对于求加权平均后的图像误差越小,但同时搜索范围尺寸NS也要相应增大,提高了算法复杂度。最终估计中需要进行第二次相似块分组,取值一般与Nmax相等。

4)在相似块搜索过程中,设定的阈值τ1过小,则指定区域内搜索到的相似块个数越少,加权平均后估计值误差偏大;τ1过大,搜索到的相似块个数超出设定值,提高了算法复杂度。阈值τ1的取值要参考原图像相邻像元灰度值的差值,结合海洋场景的特点,相距越近的像元灰度值一般差异越小,因此与处理陆地SAR图像相比,τ1的取值应适当减小。在第二步维纳滤波之前,需要对基础估计得到的图像和原图像再次进行相似块分组,阈值一般比τ1小,以达到进一步去噪的目的。

5)硬阈值收缩步骤中设定的阈值λ3D对于去噪效果有一定影响。根据公式(4),λ3D越小,变换系数r收缩门限也越小,不能完全滤除相似块组成的三维矩阵中的噪声;λ3D过大,门限提高,导致除噪声外一部分有用信息也被滤除,使得去噪效果下降。

6)针对图像噪声较强时BM3D算法去噪性能明显下降的问题,文献[11]提出了一种解决的方法,在基础估计步骤中,计算块间距离之前先对各块进行二维预滤波,即对每一块进行二维变换,然后用一个相对较小的硬阈值收缩变换系数已达到降噪的目的。这种方法可以缓解因噪声过强而导致的块匹配失真,得到新的块匹配距离公式：

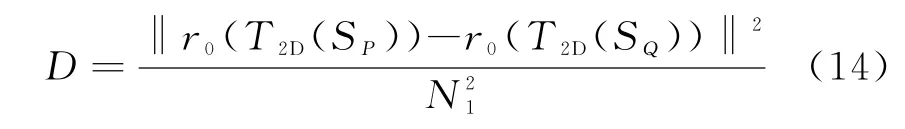
其中,预滤波阈值为λ2Dσ,T2D为二维变换,实际操作是将第一步中的二维正交小波变换(2D-Bior)改为二维余弦变换(2D-DCT)。值得一提的是,如果选用余弦变换代替正交小波变换,则搜索窗尺寸N1不必等于2的幂,但也一般在[8,16]范围内取值。

2.2 仿真实验

本文仿真实验环境为Intel i5(2.67 GHz)、16 GB内存处理器,针对算法的评价指标主要为去噪后图像与原始图像的峰值信噪比(PSNR),如式(15)所示,次要考虑运算时间。

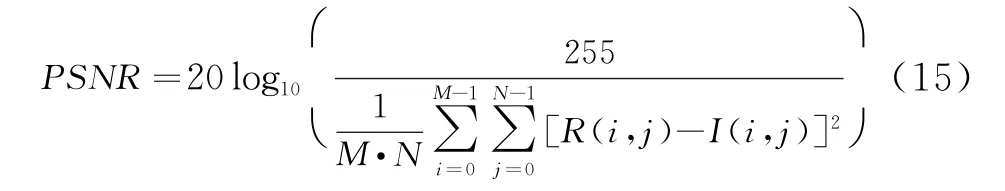
式中 ,I,R分别为去噪前后图像,大小为M×N。PSNR反映了图像处理前后的失真程度,其值越大,表明去噪前后图像灰度值差异越小,一定程度上表明去噪效果较好。

图2(a)显示了一幅不含噪声的仿真海面SAR图像,大小为3 000×3 000,有两道明显的波浪,将图像量化至[0,255]灰度范围;向其中混入均值为0、方差为σ2的加性高斯白噪声(分为强噪声σ=50和弱噪声σ=20两种情况),得到含噪图像如图2(b)所示。表1和表2显示了初始设定的BM3D算法参数,根据参数选择原则,逐项改进并对比去噪结果,总结具体参数的合理取值范围。

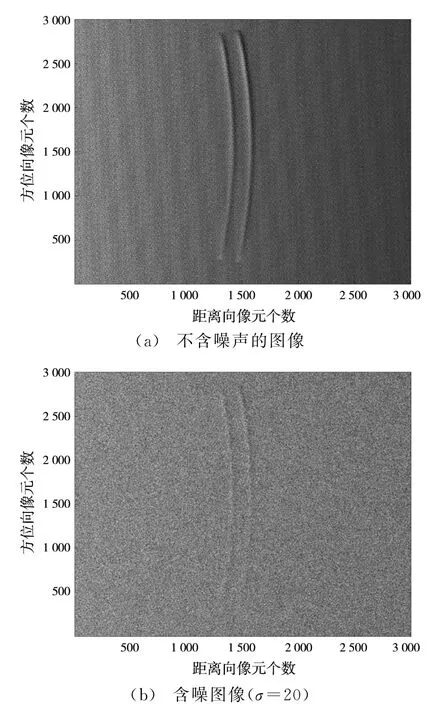
图2 仿真海面SAR图像

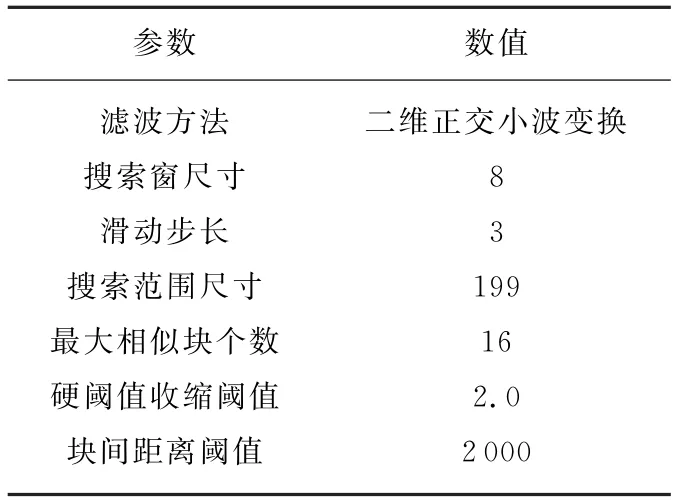
表1 初始BM3D算法基础估计参数

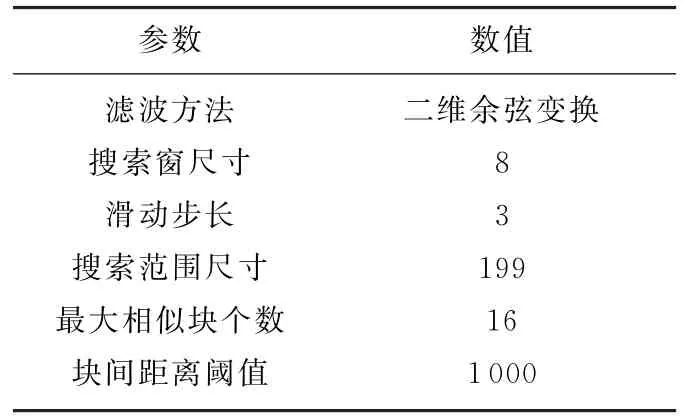
表2 初始BM3D算法最终估计参数

表3给出了搜索窗尺寸N1对去噪的影响。图3直观地显示了表3数据的变化趋势。从中发现,窗尺寸主要影响了算法运算时间,一般N1取值8或16能得到较好的去噪效果。

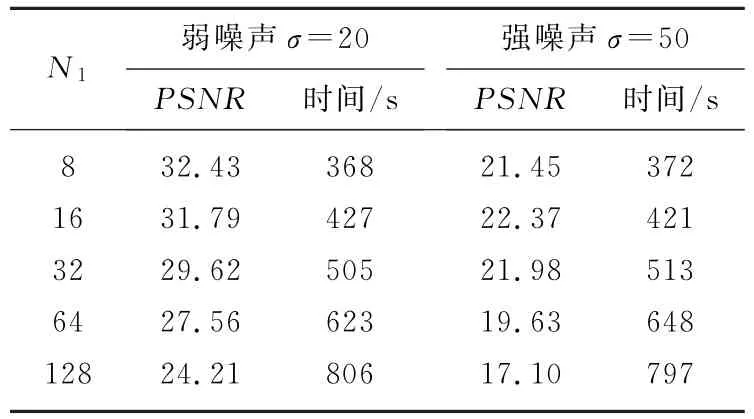
表3 搜索窗尺寸对去噪的影响

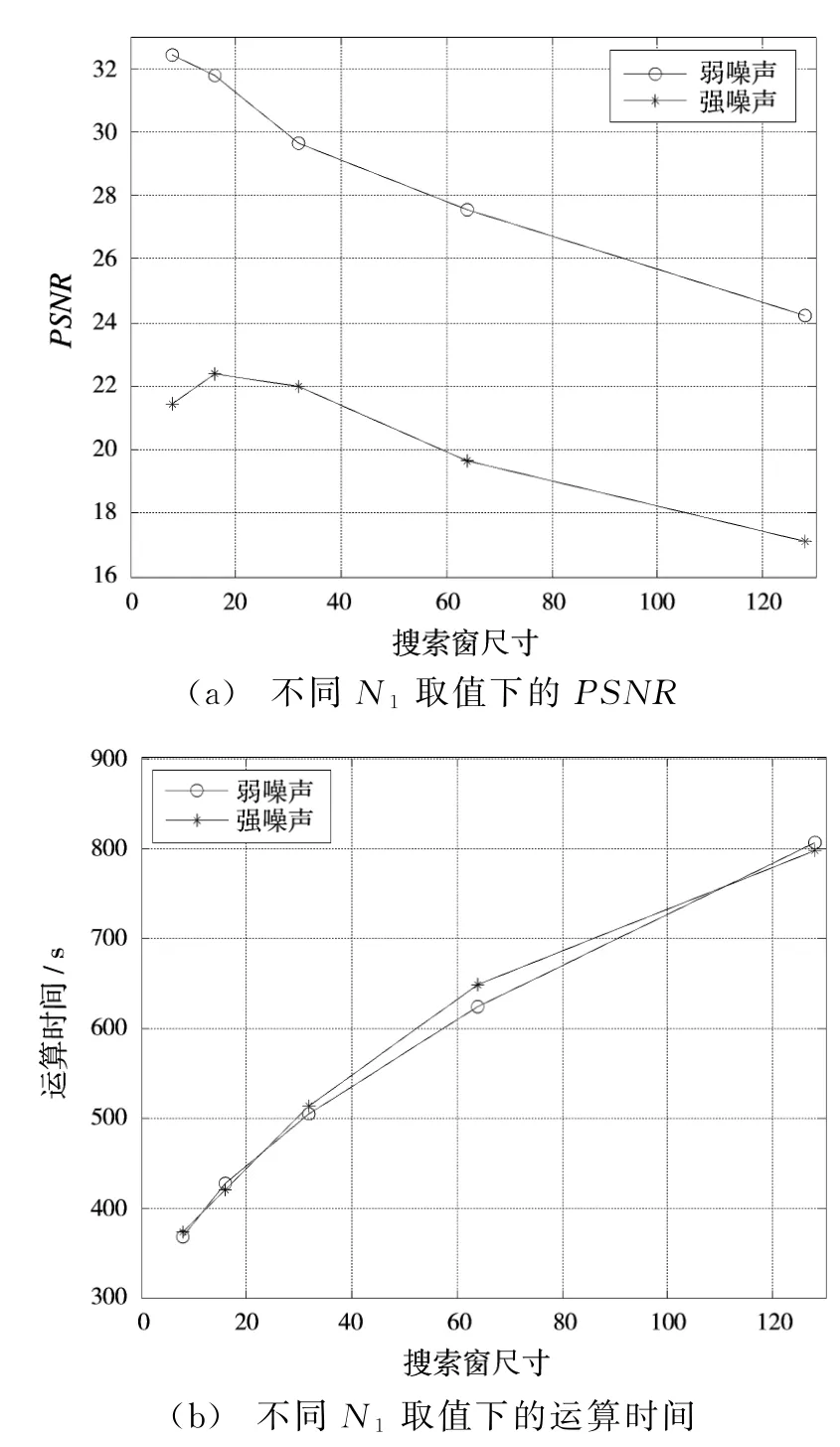
图3 搜索窗尺寸对去噪的影响

图4显示了最大相似块个数对去噪的影响。由实验数据可知,Nmax过大时,算法运算时间急剧增加,Nmax在[20,40]范围内取值能够得到较好的去噪效果。

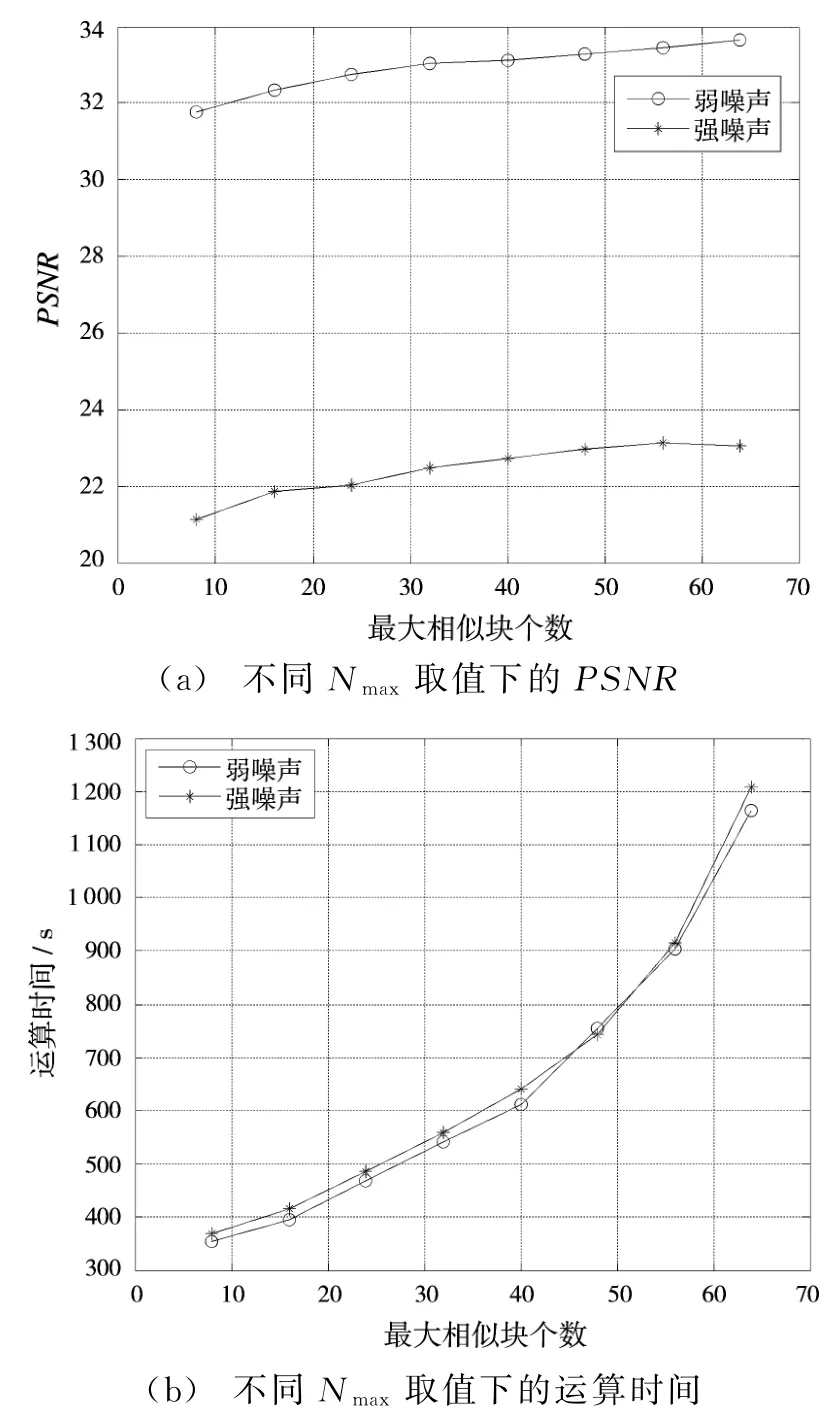
图4 最大相似块个数对去噪的影响

图5显示了基础估计中块间距离阈值τ1对去噪的影响,τ1取值在[3000,5000]范围内效果较好。图6显示了最终估计中块间距离阈值对去噪的影响,取值在[2 000,3 000]范围内效果较好。

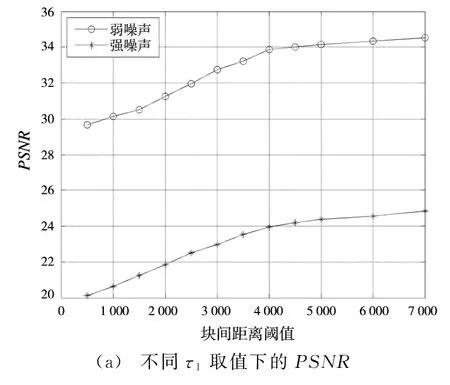
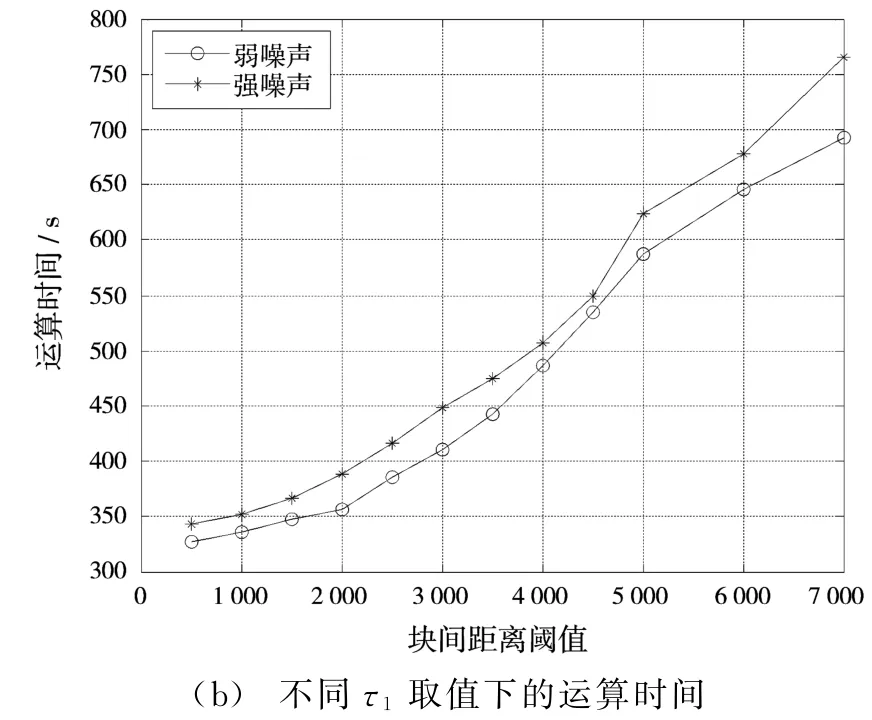
图5 基础估计中块间距离阈值对去噪的影响

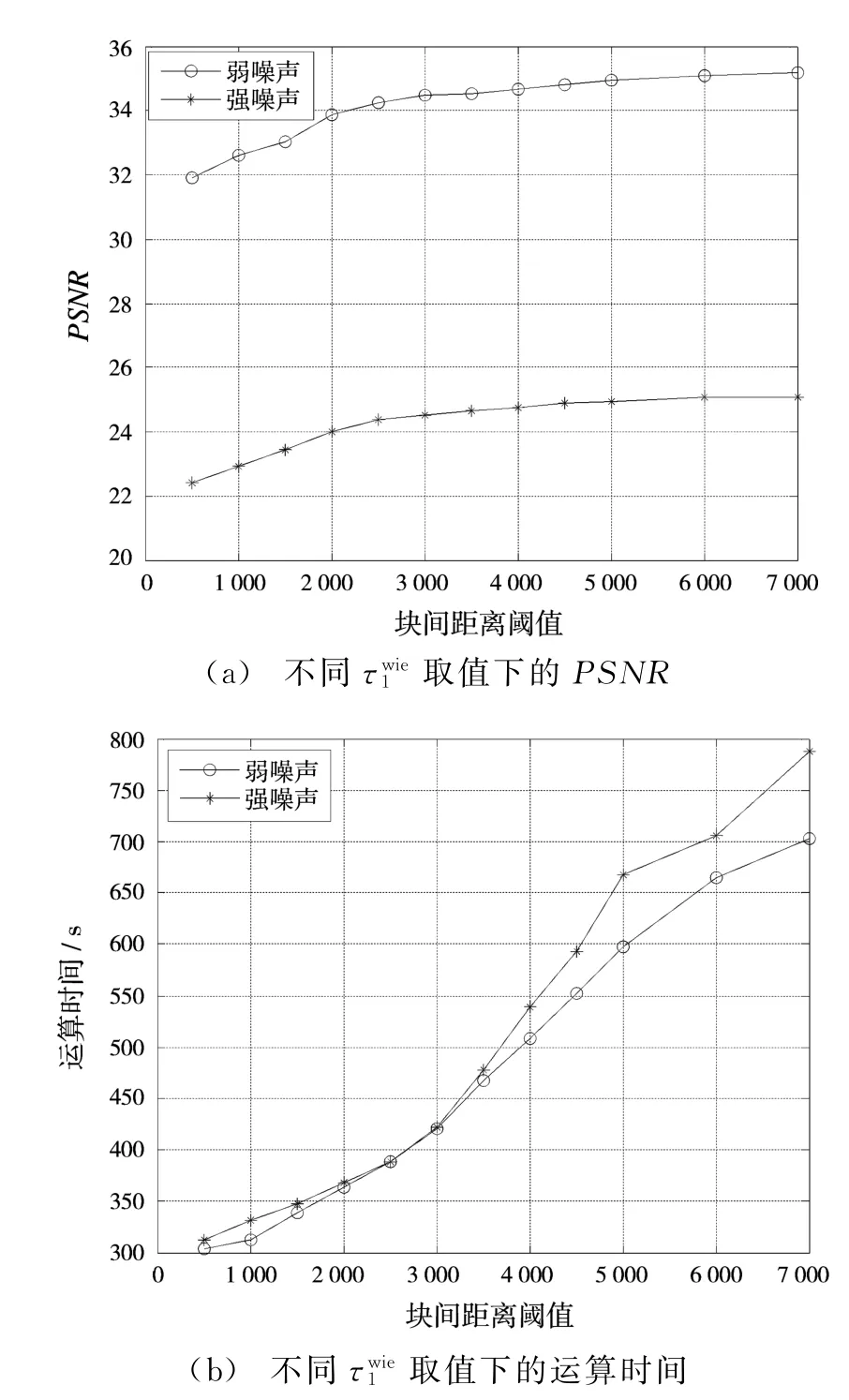
图6 最终估计中块间距离阈值对去噪的影响

图7显示了硬阈值收缩阈值λ3D对去噪的影响。当噪声较弱时,λ3D取值在3.0左右能够得到较好的去噪效果,但随着噪声增强,λ3D的取值也应随着适当增加。

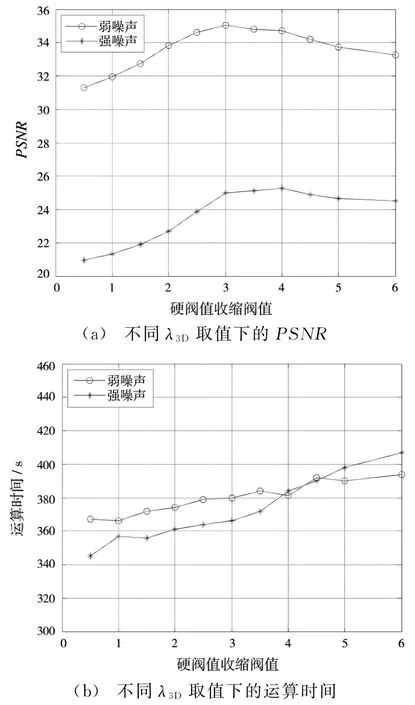
图7 硬阈值收缩阈值对去噪的影响

根据参数选择原则6),比较不同滤波方法对不同强度噪声图像的去噪效果,如图8所示,初始假设λ2D=1.0。从中可知,当噪声强度较大时,采用余弦变换的效果要比小波变换好,运算时间也较少。图9显示了预滤波过程中收缩阈值λ2D对去噪的影响。可以发现,λ2D取值在2.0左右能够对强噪图像有较好的处理效果。

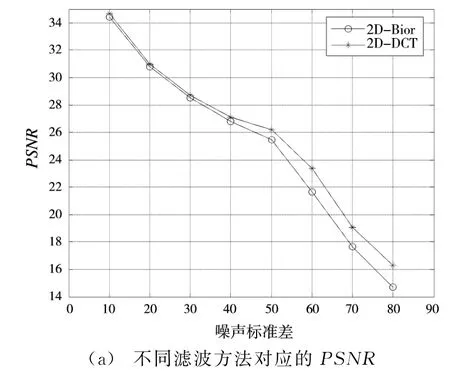
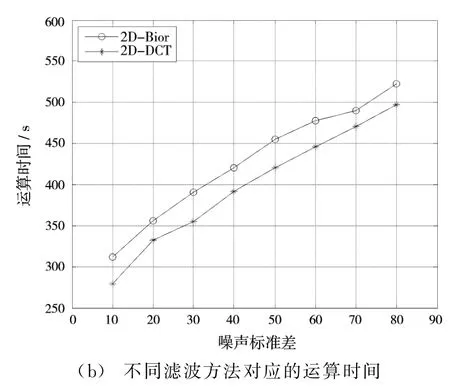
图8 不同滤波方法对不同强度噪声图像去噪的影响

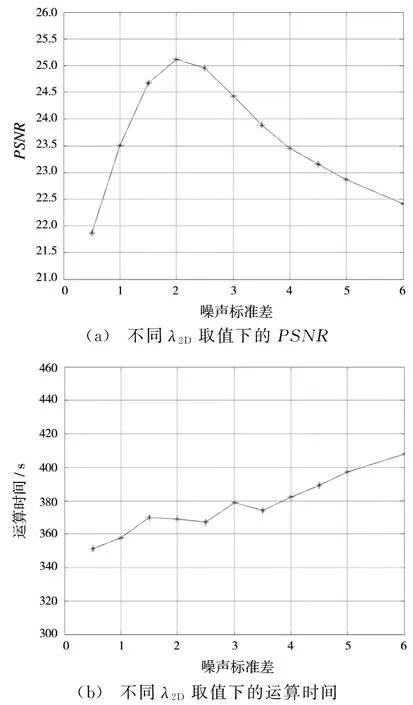
图9 预滤波阈值对强噪图像σ=50去噪的影响

3 实测数据验证

图10(a)显示了一景2010年7月5日海南岛东部海域获取的Radarsat-2幅度图像,大小3 000×3 000,分辨率约为10 m×10 m。由于相干斑是乘性噪声,需要将原图像进行对数变换,转换成加性噪声,并量化至[0,255]灰度范围,如图10(b)所示。采用分块法[13]估计图10(b)的噪声标准差,得到估计值σ=46.22,属于较强噪声的情况。根据本文讨论的BM3D算法参数选择原则,选取一组合适的参数如表4和表5所示。

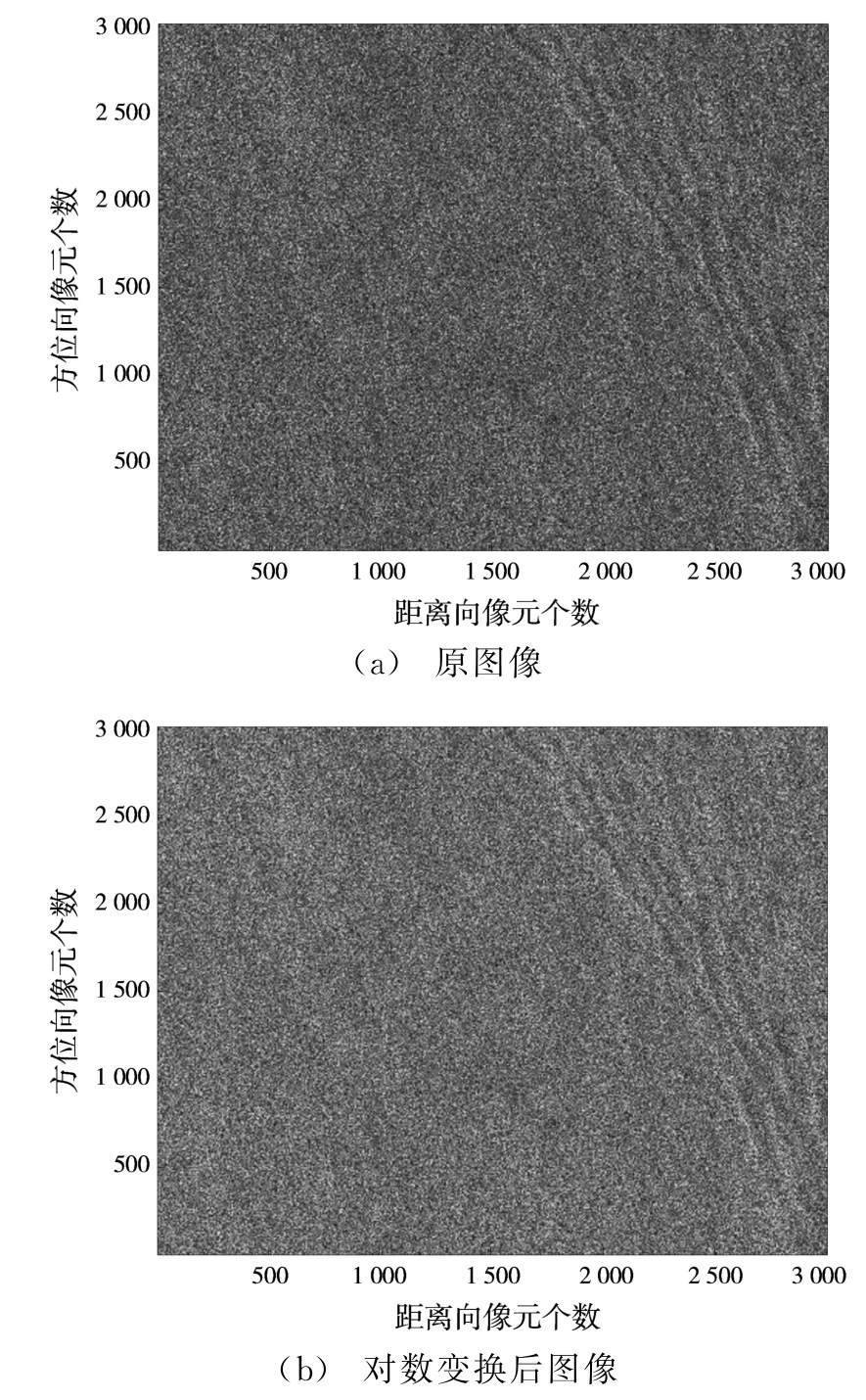
图10 实测海洋SAR图像

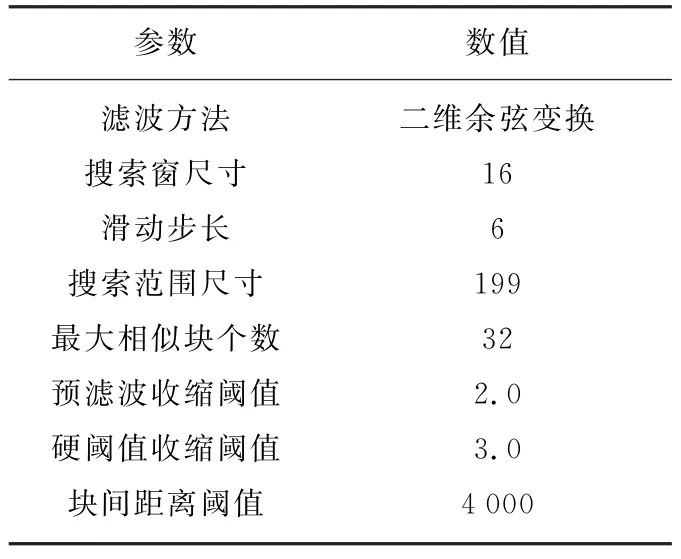
表4 改进BM3D算法基础估计参数

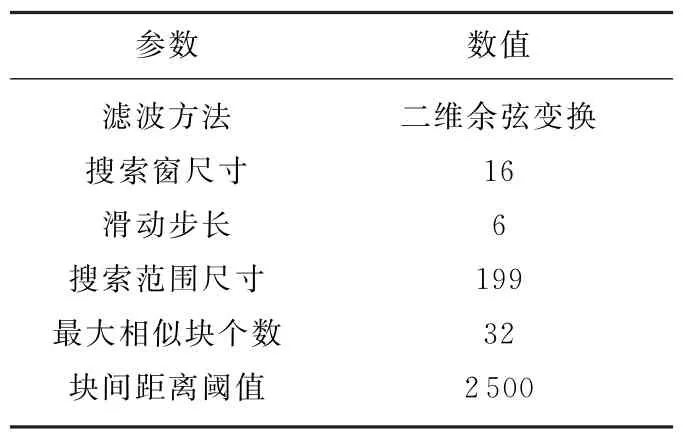
表5 改进BM3D算法最终估计参数

对比Lee滤波、Frost滤波、增强Lee滤波、小波软阈值滤波和两组不同参数下的BM3D算法去噪结果,选用的去噪效果评价指标有图像均值¯I、标准差std和等效视数ENL,如表6所示。滤波前后同一区域均值变化越小,表明图像细节信息得到很好的保持;而标准差变化越大,表明噪声滤除效果越好。由功率图像均匀区域计算等效视数,等效视数越大,表明相干斑噪声越弱。图11显示了去噪后的SAR图像,其中BM3D算法和小波软阈值滤波对应的去噪图像需要对数逆变换。可以看出,选择表4和表5参数下的BM3D算法去噪图像等效视数最大,视觉效果也最好。

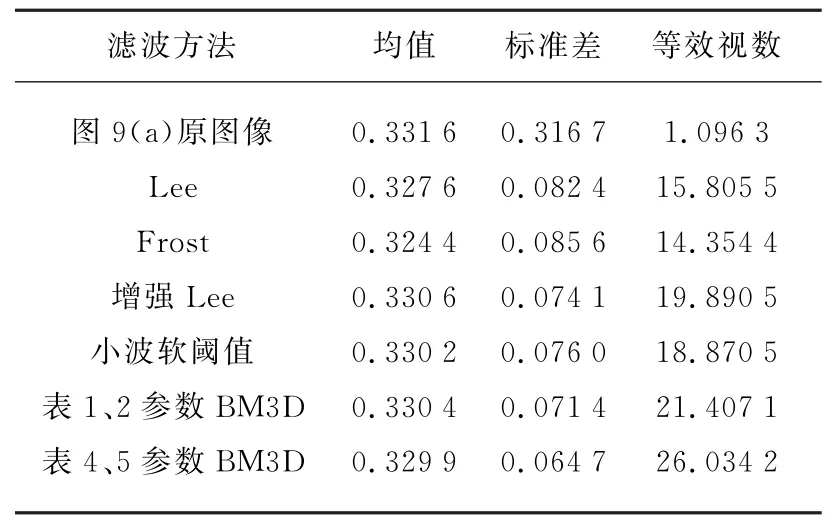
表6 各方法去噪性能对比

4 结束语

BM3D算法对于加性噪声图像具有很好的去噪效果,本文将其应用于SAR图像乘性相干斑噪声的滤除中,针对场景相似性较高的海洋SAR图像,通过大量实验总结了BM3D算法参数的选择原则。并通过实测数据验证,在强噪声条件下选择适当的BM3D参数,能够达到较好的去噪性能。在下一步中,通过将BM3D算法与小波变换、非局部平均等思想相结合来进一步提高去噪效果也是很有意义的研究方向。

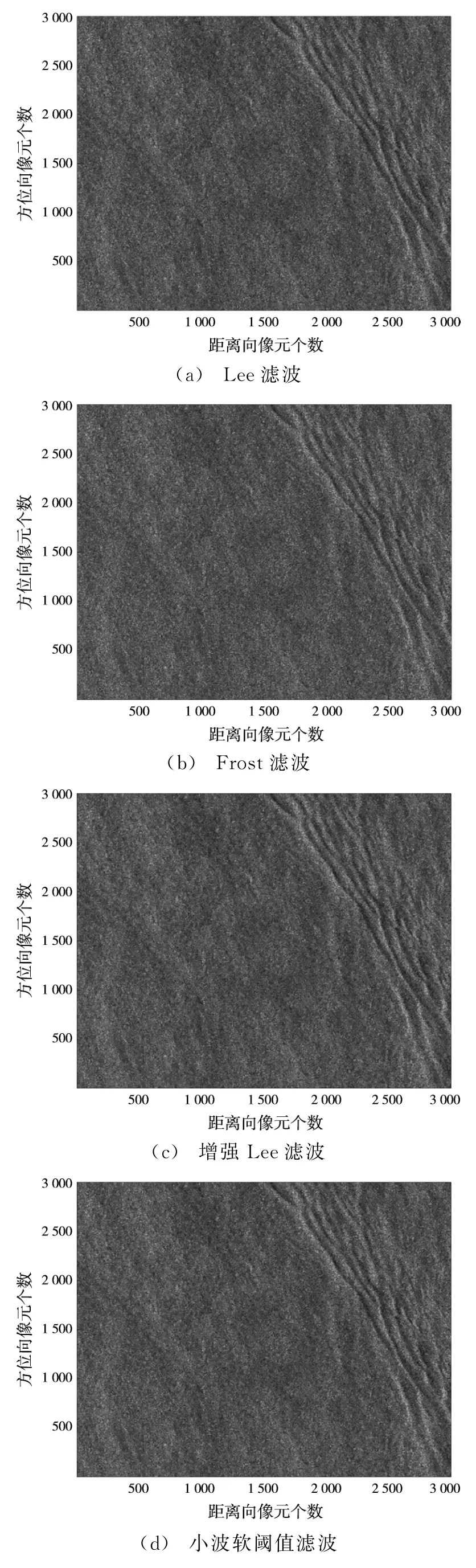
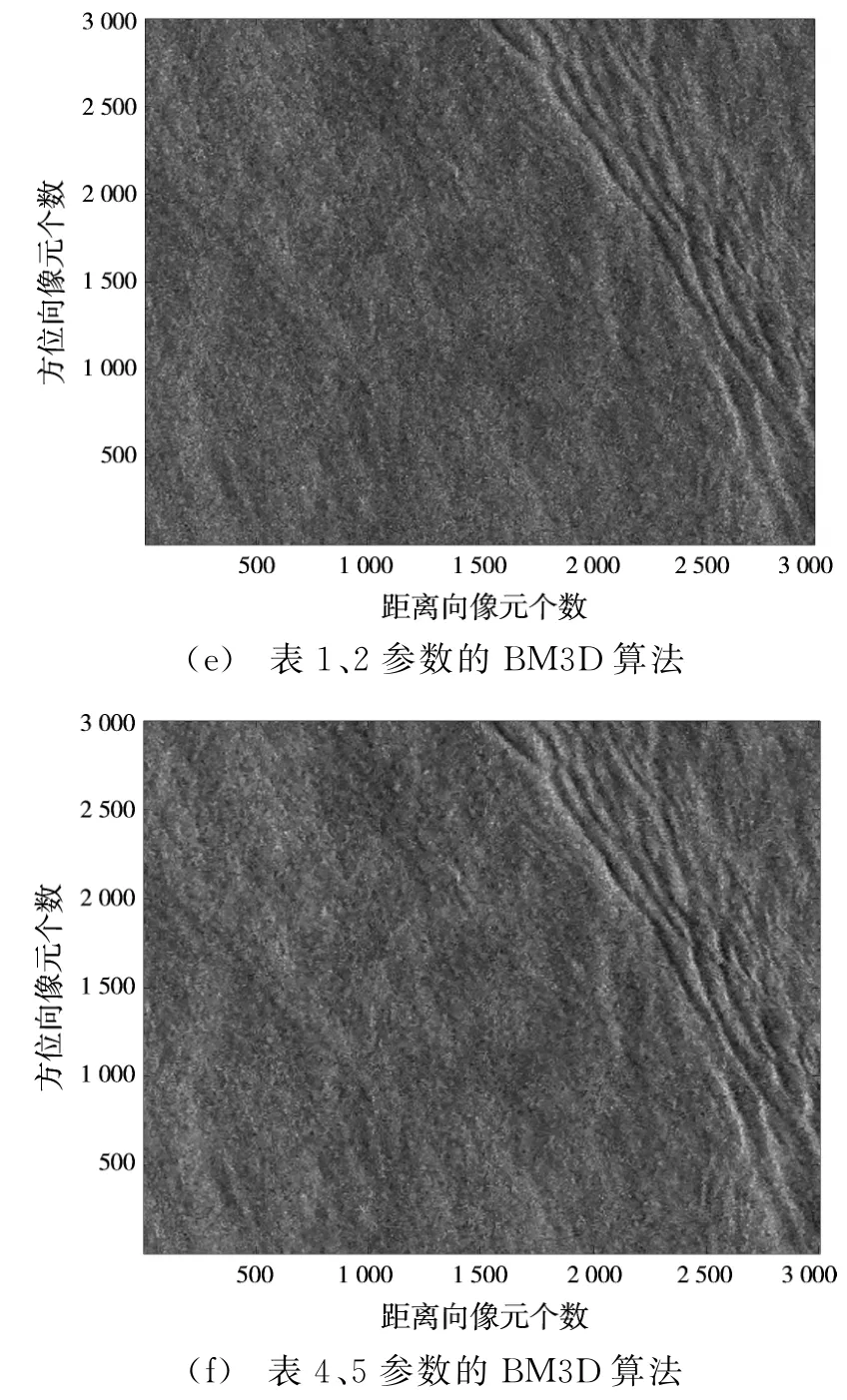
图11 去噪图像对比

[1]徐颖,周焰.SAR图像相干斑抑制研究进展[J].计算机工程与应用,2013,49(20)：210-216.

[2]YAROSLAVSKY L P,EGIAZARIAN K O,ASTOLA J T.Transform Domain Image Restoration Methods：Review,Comparison and Interpretation[C]∥Proceedings of SPIE 4304.Nonlinear Image Processing and Pattern Analysis XII.[S.l.]：[s.n.],2001：155-169.

[3]陈建宏,赵拥军,黄洁,等.改进的多视PolSAR非局部均值滤波算法[J].测绘科学技术学报,2014,31(5)：496-501.

[4]袁珍,林相波,王新宁.滤除图像中混合噪声的LES模型[J].信号处理,2013,29(10)：1329-1335.

[5]谢志昌,尹东,孙涛.基于块匹配的迭代滤波SAR图像去噪[J].光电工程,2015,42(1)：65-71.

[6]HOU Yingkun,ZHAO Chunxia,YANG Deyun,et al.Comments on“Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering”[J].IEEE Trans on Image Processing,2011,20(1)：268-270.

[7]刘向乐,冯象初.小波域三维块匹配图像去噪[J].计算机工程与应用,2010,46(16)：185-187.

[8]王永兴,蒲亦非,巩晓倩,等.分数阶三维块匹配去噪算法[J].计算机应用研究,2015,32(1)：287-290.

[9]DABOV K,FOI A,KATKOVNIK V,et al.Image Denoising with Block-Matching and 3D Filtering[C]∥Proceedings of SPIE 6064.Image Processing：Algorithms and Systems,Neural Networks,and Machine Learning.[S.l.]：[s.n.],2006：1155-1164.

[10]BUADES A,COLL B,MOREL J M.Nonlocal Image and Movie Denoising[J].International Journal of Computer Vision,2008,76(2)：125-138.

[11]DABOV K,FOI A,KATKOVNIK V,et al.Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering[J].IEEE Trans on Image Processing,2007,16(8)：2082-2094.

[12]黄牧,黄文清,李俊柏,等.基于BM3D图像去噪算法的参数研究[J].工业控制计算机,2014,27(10)：99-101.

[13]赖施成,贾泂.基于块内邻域相关度的图像噪声估计[J].计算机与现代化,2009(12)：82-88.