基于PHD的多目标检测前跟踪改进方法∗

柳 超,关 键,黄 勇,王国庆

(1.海军航空工程学院电子信息工程系,山东烟台264001;

2.中国人民解放军92853部队,辽宁葫芦岛125106;

3.海军航空工程学院信息融合技术研究所,山东烟台264001)

0 引言

多目标检测前跟踪问题是当前微弱目标检测和数据融合领域研究的热点和难点问题,其难点主要体现在多目标环境下往往需要复杂的数据关联[1-2]。文献[3]提出了一种基于粒子滤波的多目标检测前跟踪方法,虽然可以避免数据关联,但是当目标数大于2个时,状态转移矩阵的讨论和计算都变得非常复杂,很难推广应用到目标数更多的场合。

近年来,基于有限集统计学理论(Finite Set Statistics Theory,FISST)的多传感器多目标跟踪方法得到了快速发展。这种方法通过随机有限集建模并利用集合的微积分运算推导出最优多目标贝叶斯滤波器,成功地规避了数据关联所带来的困难和麻烦。2003年,Mahler提出了概率假设密度(Probability Hypothesis Density,PHD)滤波器[4],其实质是随机集多目标状态在其后验概率密度下的一阶矩,相比最优多目标贝叶斯滤波器,PHD滤波器的运算复杂度有很大降低;之后,Vo给出了PHD滤波器的两种收敛实现方式：序贯蒙特卡洛PHD[5],也称概率假设密度粒子滤波(Particle Filter PHD,PF-PHD),和高斯混合PHD[6](Gaussian Mixture PHD,GM-PHD),使得基于FISST的多目标跟踪方法向工程应用迈进了一大步。

在PHD的检测前跟踪应用方面,Punithakumar K在文献[7]中首次将PF-PHD应用于红外图像的多目标TBD中,提出了PF-PHD-TBD方法。该方法引入多目标跟踪的思想,建立起目标的运动模型和传感器测量模型,在信噪比较低的情况下取得了较好的效果,证明了PFPHD-TBD方法在多个微弱目标检测及跟踪方面的有效性。由于该方法对目标数目和状态的估计精度还不够高,文献[8-12]等又各自从不同角度对PF-PHD-TBD算法进行改进,并分别取得了一定效果。

目前,PF-PHD-TBD性能表现不佳的原因,除了信号层观测模型建立不准确导致的测量值不满足理论假设外,其仅仅采用基本粒子滤波实现对PHD近似也是一个重要原因。尤其当目标维数较高时,不仅计算复杂,而且对权重起作用的因素往往只是与测量值有直接关联的状态矢量,与测量无关的状态矢量没有被充分利用,由此导致粒子权重之和即目标的数目估计不准确,从而造成聚类不稳定和状态估计精度低等问题。Rao-Blackwellised粒子滤波(RBPF)[13-15]被认为是通过边缘化线性变量减少状态空间维数的有效办法。与基本粒子滤波相比,它将目标的状态空间进行降维分解,分别运用线性与非线性滤波器进行处理,显著降低了粒子状态维数,减少了所需粒子数和计算量,并且充分利用各维状态矢量的信息,提高了状态估计精度。在RBPF滤波与随机有限集结合方面,文献[16-17]分别作出了尝试,将RBPF应用于多目标的跟踪,取得了不错的效果,但是目前尚未见到RBPF应用于随机集多目标检测前跟踪的相关文献。因此,本文提出一种结合RBPF的PFPHD-TBD方法,用于改进随机集框架下多目标检测前跟踪的性能。

1 状态模型及观测模型建立

1.1 目标运动模型

假设在k时刻目标的数目为N k,目标的状态为5维向量：

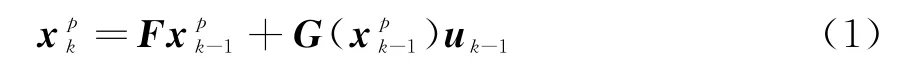
式中,F为状态转移矩阵,u k为独立的高斯白噪声。u k～N(0,Q k),其中Q k为噪声协方差。包含所有目标的观测集合为

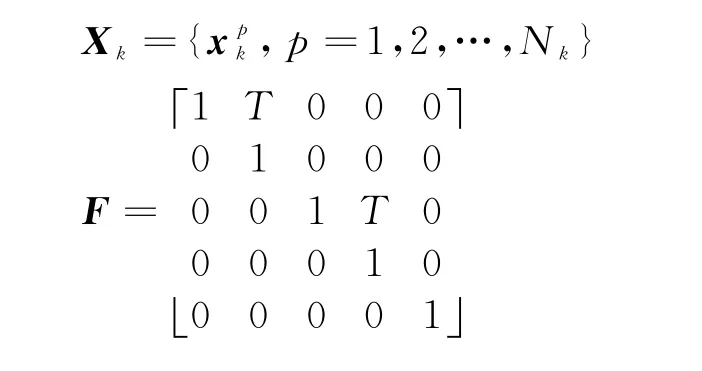
1.2 传感器观测模型

将回波信号表示为距离-多普勒-方位域的观测数据。设单元(i,j,l)(i=1,…,Nr,j=1,…,Nd,l=1,…,Nb,其中Nr,Nd和Nb分别表示距离、多普勒和方位的维数)处的功率观测值z(i,j,l)k为

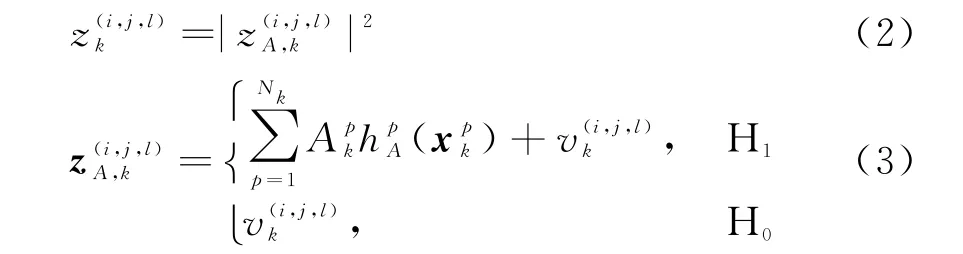
式中,H1,H0分别表示存在和不存在目标,为(i,j,l)处的观测噪声。若以,…,Nr,j=1,…,Nd,l=1,…,Nb}表示k时刻的所有量测,则联合似然函数为

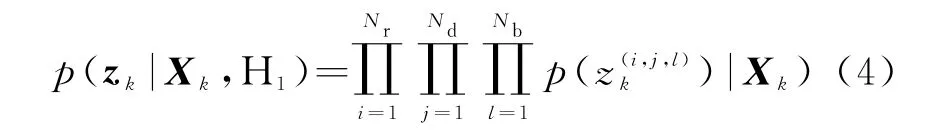
如果用Cr(s k),Cd(s k),Cb(s k)分别表示目标实际影响到的区域,则联合似然比的计算可简化为

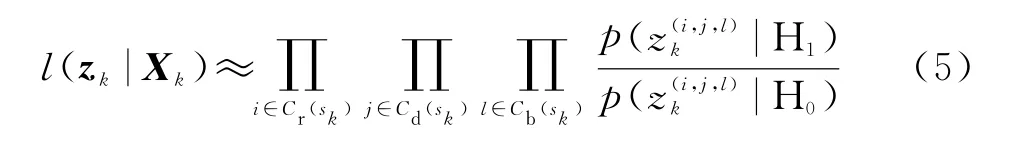
2 PF-PHD-TBD算法

在k-1时刻用一组有权重的粒子来表示目标的后验概率分布：

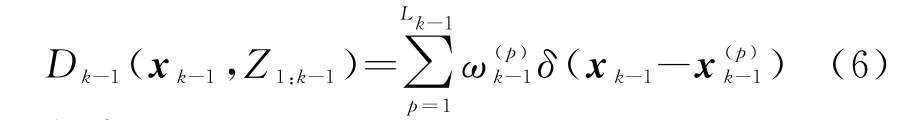
状态预测：

设k-1时刻有L k-1个粒子,k时刻新生粒子的采样数为J k,则预测密度为

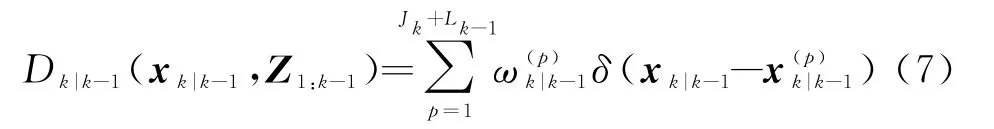
其中,对于存活粒子p=1,2,…,L k-1,按下式采样：

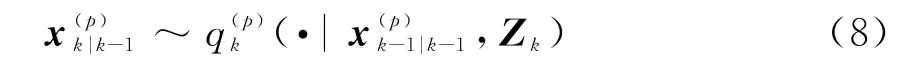
并计算其权重为

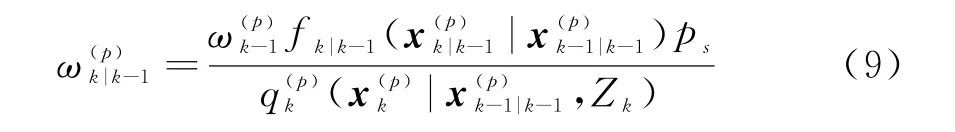
对于新生粒子p=L k-1+1,…,L k-1+J k,按下式采样：

并计算其权重为

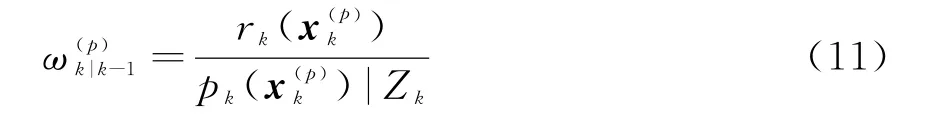
状态更新：

对于k时刻粒子p=1,…,L k-1+J k的更新权重可由下式计算：

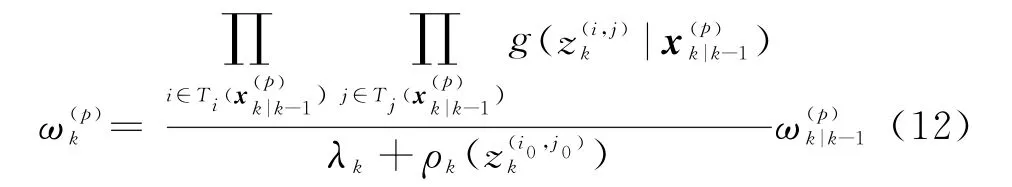
式中,λk为杂波分布的归一化常数,通常设为1,

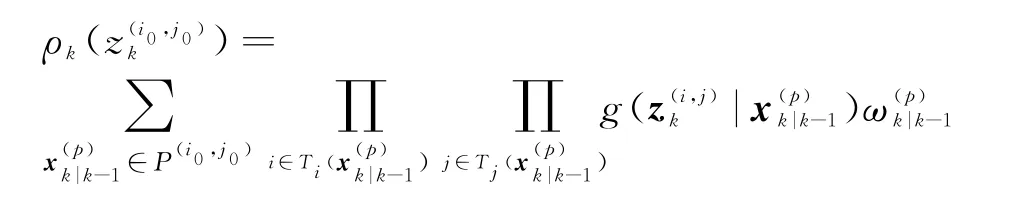
任一分辨单元(i0,j0)内粒子集合为

3 RBPF-PHD-TBD算法

将RBPF滤波与PF-PHD-TBD方法相结合,其主要思想是在粒子的预测和更新过程中,用RBPF取代基本粒子滤波,充分利用线性状态与非线性状态的关联特性,提高权重计算的准确度。其详细计算步骤如下：

步骤1 状态预测

对于k时刻“存活”粒子,先将其状态向量进行分割,,和分别表示向量x k在k时刻的线性和非线性部分,则粒子的状态方程和测量方程改写如下：

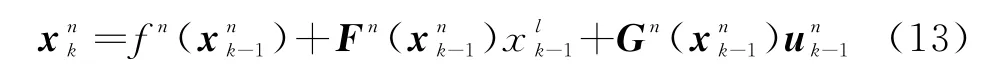
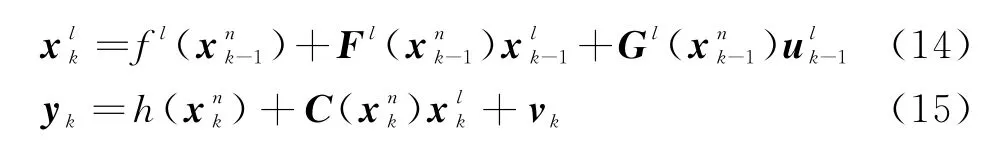
式中,;v k～N(0,R k)。

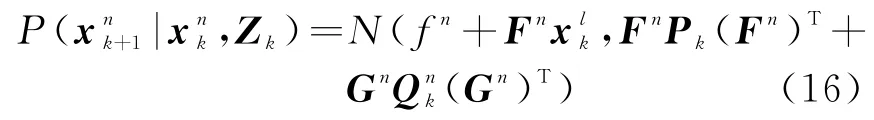
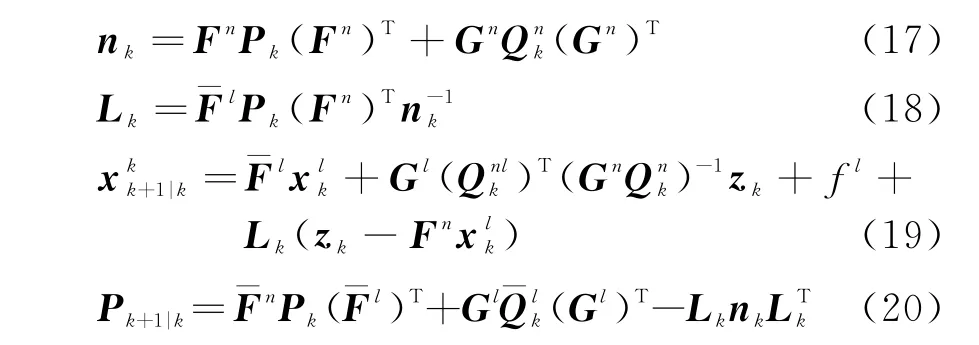
对所有的k时刻“存活”粒子,根据式(9)计算粒子的权重。

对于k时刻“新生”粒子,根据“新生”粒子初始化方法求取其状态分布和协方差,即

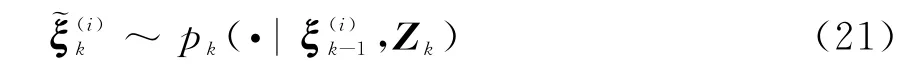
步骤2 状态更新

对于k+1时刻所有的“存活”粒子和“新生”粒子,根据式(12)计算粒子的权重,经过重采样之后提取权重较大的粒子的非线性状态作为更新后粒子的非线性状态;然后,对粒子线性部分的均值和协方差作卡尔曼滤波更新：

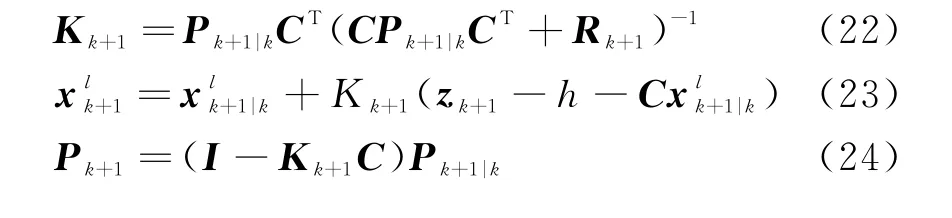
4 仿真验证

假设在雷达的观察区域内存在4个目标,各个目标在不同的时刻出现和消失,即目标数是时变的;4个目标的幅度是固定的,且都设为20;背景噪声方差根据目标功率和信噪比产生,信噪比计算公式为SNR=10 lg(P/2σ2),且SNR=9 dB;仿真时间为40帧,当前目标在下一时刻的存活概率为e k|k-1=0.95;不考虑目标分裂的情况,每一帧新生目标数目服从均值0.2的泊松过程;设定初始存活粒子数L k=2 000,每一帧新生粒子采样数J k=2 000,初始存活粒子与新生粒子均服从观测区域上的平均分布。观察区域大小为40 km×60 km。具体场景设置如表1所示。

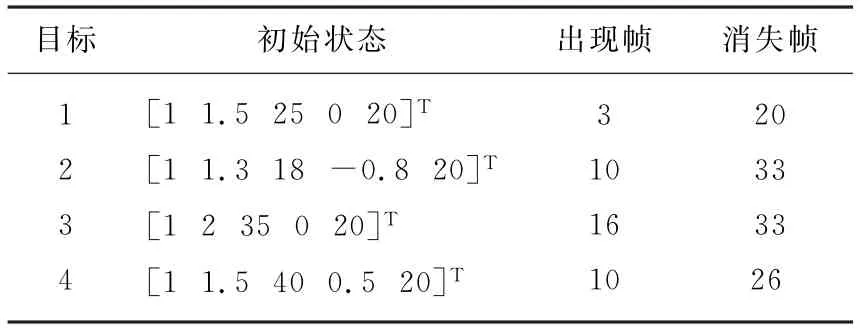
表1 目标运动状态设定

目标满足近似匀速运动模型,

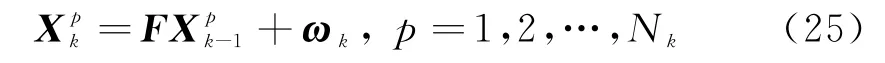
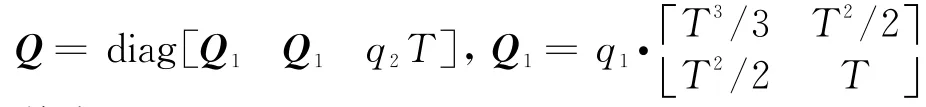
根据RBPF滤波思想可以将目标状态改写为X k=[x n,x l]T,其中x n=[x y I]表示与量测有关 的 目 标 位 置 与 强 度 信 息,表 示 独 立于量测的目标速度信息。改写后的动态方程为

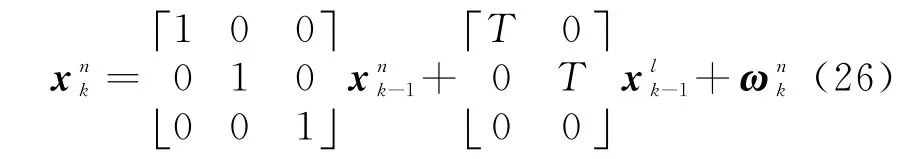
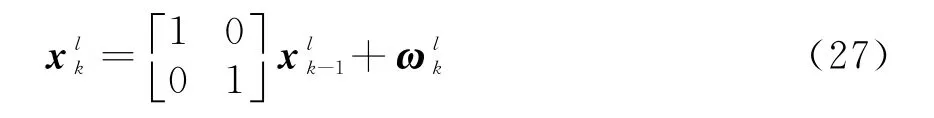
通过将目标的状态方程和量测方程与式(13)～(15)比较可以得到各个状态转移矩阵如式(28)所示;将式(28)中各公式代入式(16)～(24)可对RBPF-PHD-TBD的算法步骤进行简化。

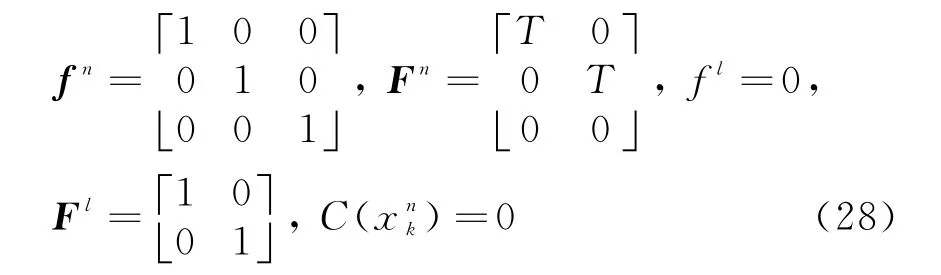
对于单目标检测前跟踪,其评价指标通常为最小均方误差;对于多目标检测前跟踪,其评价指标不容易定义,这是因为算法在估计每一个目标状态的同时还要估计目标的数目(集合的势),而真实目标状态的集合和估计得到的目标状态集合的势并不一定相等。目前评估多目标跟踪性能的方法有很多,比如最优子模式指派距离,Hausdorff距离和 Wasserstein距离等。 本文中采用Wasserstein距离,其定义为任意两个非空子集^X,X上,

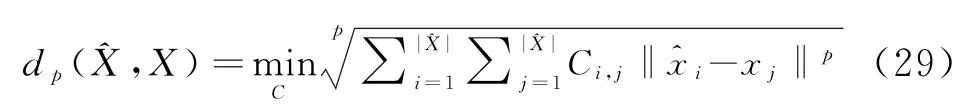
仿真结果如图1～图5及表2所示。

图1为两种算法分别对目标进行跟踪得到的粒子云状态。其中,深色的表示PF-PHD-TBD,浅色的表示RBPF-PHD-TBD。可以看到,两种算法都能较好地检测并跟踪到目标,但是PF-PHD-TBD出现了许多错误的粒子云,将会输出错误点迹,而RBPFPHD-TBD的粒子云与目标位置完全相符,不会输出错误点迹;并且,就粒子云的体积来看,RBPFPHD-TBD明显小于PF-PHD-TBD,即粒子分布更加集中,这是由于其状态估计的协方差更小。图2为对粒子提取状态后分解到两个坐标轴之后的跟踪点迹,深色的表示PF-PHD-TBD,浅色的表示RBPF-PHD-TBD。可以看到,与图1所示本质上一致,即两种算法都能跟踪上目标,但是PF-PHD-TBD会输出许多错误点迹,从而造成虚警。

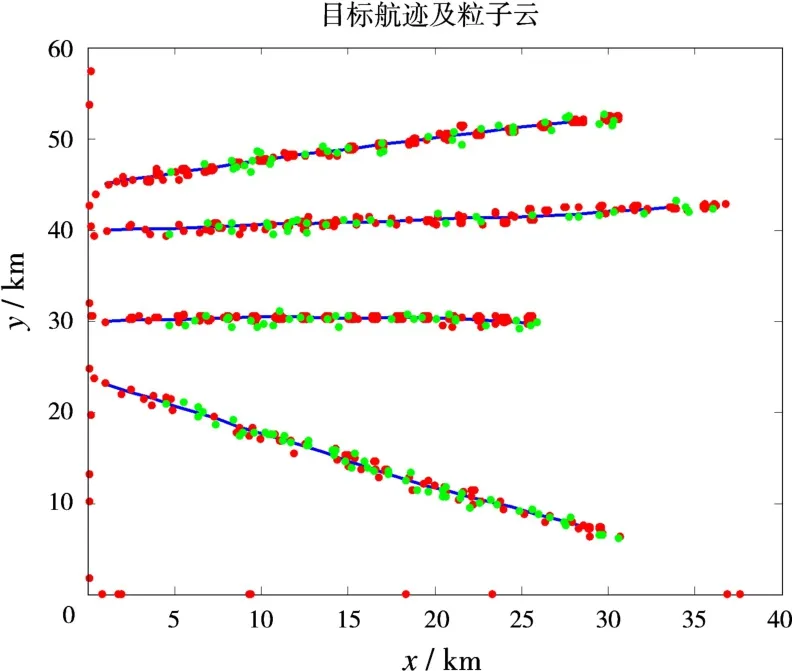
图1 目标跟踪的粒子云

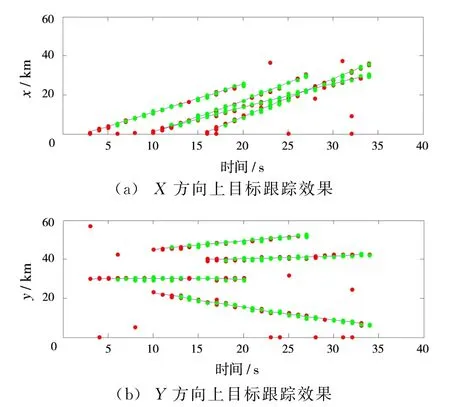
图2 分解后目标跟踪效果

图3为10次仿真后两种算法估计的目标数目平均值,从总体上看,RBPF-PHD-TBD的估计更加准确,与目标真实数目更加接近,这是由于其充分利用了各维状态信息,通过状态之间的关联实现粒子权重的更准确计算。

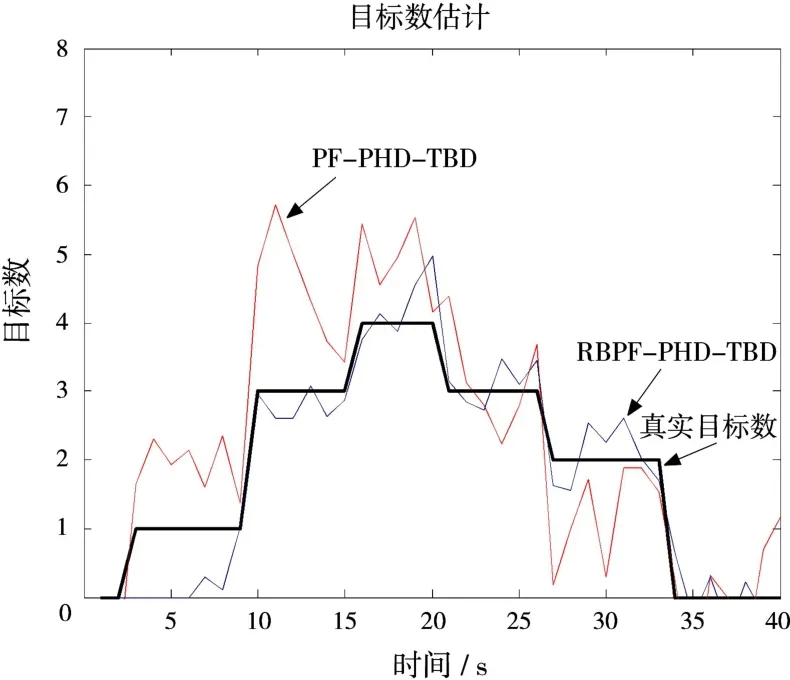
图3 目标数估计

从上述3张图中还可以看到,PF-PHD-TBD对目标数目的变化非常灵敏,一是能够在接近目标出现的时刻作出数目估计,并跟踪上目标;二是在有目标消失的时刻也响应迅速,但是却存在目标估计数变化剧烈、估计不准确的问题。相比之下,RBPF-PHD-TBD在开始时刻则有几帧延迟,需要多帧积累之后才作出响应,在其他时刻,对目标数目变化的响应也比较稳健,因此当有目标出现或消失时变化并不像PF-PHD-TBD一样剧烈。

图4为10次仿真中脱靶距离比较,可以看到在目标存在的大部分时刻,RBPF-PHD-TBD的跟踪误差都明显小于PF-PHD-TBD。

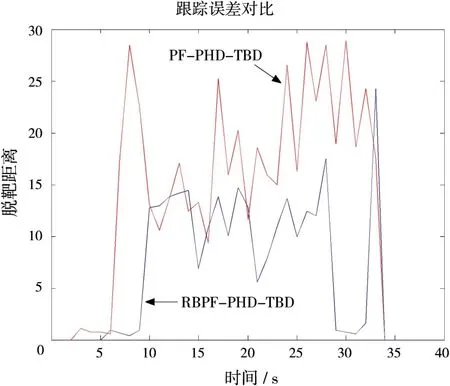
图4 Wasserstein距离

对两种算法的运行时间进行统计,求出10次实验中的运行时间并取平均值。所用电脑配置为：处理器,Core i5-4570 3.20GHz;操作系统,Win7旗舰版64位(Direct X 11);内存,8 GB(DDR3 1 600 MHz)。

表2为10次实验的平均运行时间,可以求出RBPF-PHD-TBD的运行时间大致为PF-PHDTBD的37.8%。图5为每一次实验的运行时间,其中横轴上序号11表示的是10次实验的平均运行时间。从表2与图5可以看到,采用RBPF滤波显著降低了算法的计算负担,提高了实时性。

表2 两种算法平均运行时间

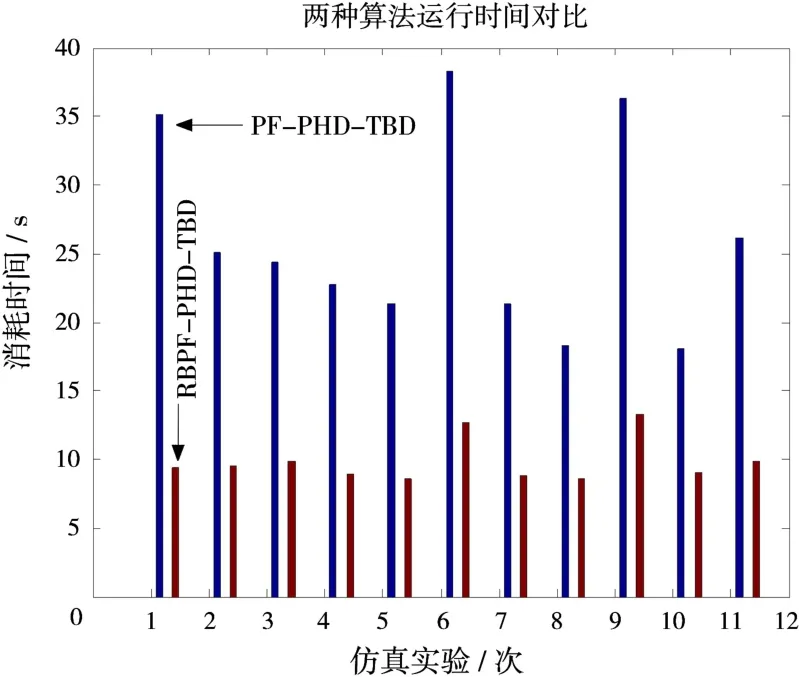
图5 两种算法运行时间

5 结束语

本文提出了一种采用Rao-Blackwellised粒子滤波的PHD多目标检测前跟踪改进方法。该方法将目标的多维状态空间进行分解,分别用线性和非线性滤波器进行跟踪,降低了传统PF-PHD-TBD的运算复杂度,使其运算时间降低为原来的大约37.8%;同时,由于充分利用了各维状态信息及状态关联特性,其对目标数目的估计更加准确,状态估计方差更小,粒子云更加集中,跟踪精度更高。

[1]王云奇,孔令讲,易伟,等.一种耦合检测和JPDA滤波的多目标跟踪算法[J].雷达科学与技术,2014,12(2)：143-148.

WANG Yuqi,KONG Lingjiang,YI Wei,et al.Integration of Detection with JPDAF for Multi-Target Tracking[J].Radar Science and Technology,2014,12(2)：143-148.(in Chinese)

[2]尹帅,袁俊泉,吴顺华,等.一种改进的JIPDA多目标跟踪算法[J].雷达科学与技术,2014,12(3)：285--290.

YIN Shuai,YUAN Junquan,WU Shunhua,et al.An Improved JIPOA Algorithm for Multi-Target Tracking[J].Radar Science and Technology,2014,12(3)：285-290.(in Chinese)

[3]BOERS Y,DRIESSEN J N.Multitarget Particle Filter Track-Before-Detect Application[J].IEE Proceedings Radar,Sonar and Navigation,2004,151(6)：351-357.

[4]MAHLER R.Multitarget Bayes Filtering via First-Order Multitarget Moments[J].IEEE Trans on Aerospace and Electronics Systems,2003,39(4)：1152-1178.

[5]VO B N,SINGH S,DOUCET A.Sequential Monte Carlo Methods for Multitarget Filtering with Random Finite Sets[J].IEEE Trans on Aerospace and Electronics Systems,2005,41(4)：1224-1245.

[6]VO B N,MA W K.The Gaussian Mixture Probability Hypothesis Density Filter[J].IEEE Trans on Signal Processing,2006,54(11)：4091-4104.

[7]PUNITHAKUMAR K,KIRUBARAJAN T,SINHA A.A Sequential Monte Carlo Probability Hypothesis Density Algorithm for Multitarget Track-Before-Detect[C]∥17th Conference on Signal and Data Processing of Small Targets,San Diego,CA：SPIE,2005：1-8.

[8]HABTEMARIAM B K,THARMARASA R,KIRUBARAJAN T.PHD Filter Based Track-Before-Detect for MIMO Radars[J].Signal Processing,2012,92(3)：667-678.

[9]林再平,周一宇,安玮.改进的概率假设密度滤波多目标检测前跟踪算法[J].红外与毫米波学报,2012,31(5)：475-480.

[10]占荣辉,刘盛启,欧建平,等.基于序贯蒙特卡罗概率假设密度滤波的多目标检测前跟踪改进算法[J].电子与信息学报,2014,36(11)：2593-2599.

[11]林再平,周一宇,安玮,等.基于概率假设密度滤波平滑器的检测前跟踪算法[J].光学学报,2012,32(10)：1-8.

[12]LEHMANN F.Recursive Bayesian Filtering for Multitarget Track-Before-Detect in Passive Radars[J].IEEE Trans on Aerospace and Electronics Systems,2012,48(3)：2458-2480.

[13]胡振涛,付春玲,刘先省.基于RB粒子滤波的多传感器目标跟踪融合算法[J].光电子·激光,2012,23(3)：566-571.

[14]GONZALEZ-DUARTE S,CHACON-MURGUIA M I.Rao-Blackwellized Particle Filter for Multiple Object Tracking in Video Analysis[C]∥11th International Conference on Electrical Engineering,Computing Science and Automatic Control,Campeche：IEEE,2014：978-985.

[15]赵增顺,林艳艳,冯翔,等.基于高斯粒子群优化的RBPF滤波算法[J].计算机应用研究,2015,32(2)：423-426.

[16]VIHOLA M.Rao-Blackwellised Particle Filtering in Random Set Multitarget Tracking[J].IEEE Trans on Aerospace and Electronics Systems,2007,43(2)：689-705.

[17]庄泽森,张建秋,尹建君.Rao-Blackwellised粒子概率假设密度滤波算法[J].航空学报,2009,30(4)：698-705.