一类幂指函数的导数及极限公式的推导
2016-01-09刘家保,余国锋,朱家明
一类幂指函数的导数及极限公式的推导
刘家保1,余国锋2,朱家明3
( 1.安徽新华学院公共课程部,安徽合肥230088;2.安徽工商职业学院教务处,安徽 合肥231131;
3.安徽财经大学统计与应用数学学院,安徽蚌埠233030)
[摘要]通过对一般幂值函数y=u(x)v(x),(u(x)>0)的求导,推导出更复杂的幂指函数y=f(x)u(x)v(x),(f(x),u(x)>0)的求导公式与极限运算,得出了极限运算定理,并通过实例验证其正确性.
[关键词]幂指函数;导数公式;极限[收稿日期]2015-08-05
[基金项目]安徽省重点自然科学
[作者简介]刘家保(1982-),男,安徽六安人,安徽新华学院公共课程部副教授,博士,主要从事复杂网络与图论的研究.
[中图分类号]O171 [文献标识码]A
0引言
设函数f(x)和g(x)为区间D上的连续函数,其中f(x)>0,x∈D称形如y=f(x)g(x)的函数为定义在D上的幂指函数.幂指函数是一类特殊的函数,对于幂指函数的导数和极限的求法,有很多相关的研究成果[1-8].对于更复杂的幂指函数y=f(x)u(x)v(x),(f(x),u(x)>0)在经济管理中也经常出现,但对于这类幂指函数的求导和求极限运算一直是个难点,故本文总结了复杂幂指函数导数的求法,并给出了幂指函数各种类型未定式的极限求法.
1幂指函数的导数求法
1.1求幂指函数y=f(x)u(x)v(x),(f(x),u(x)>0)的导数
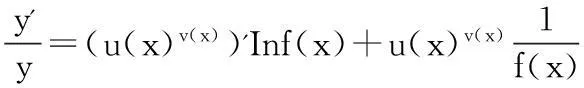
方法2:对y=f(x)u(x)v(x),(f(x),u(x)>0)两边同时取对数,即Iny=u(x)v(x)Inf(x),然后两边同时再取对数,即In(Iny)=v(x)Inu(x)+In(Inf(x)),两边同时再关于求导,即可得:
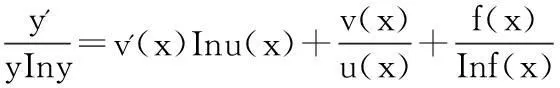
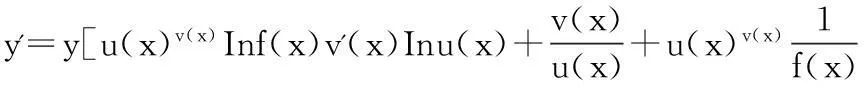
例1:设y=xxx,求y'.
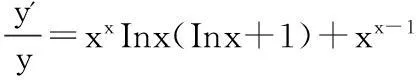
两边同乘以,可得y'=xxx[xxInx(Inx+1)+xx-1].
方法2:公式法:公式中f(x)=u(x)=v(x)=x,代入上式可得y'=xxx[xxInx(Inx+1)+xx-1].
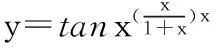

2幂指函数的极限求法

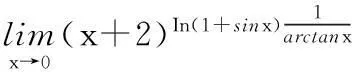

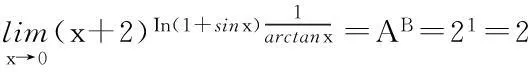
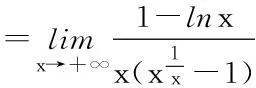
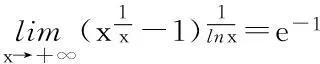
3小结
幂指函数是一类非常重要的函数,它在实际生活中经常遇到.因此,更进一步地了解和掌握幂指函数的各种性质,对解决一些实际问题非常重要.
参考文献
[1] 陈传璋, 金福临.数学分析(上)[M].北京:高等教育出版社,1983:81-93.
[2] 张勇军.一类幂指函数求导公式的推导[J].海南大学学报,2012,2(1):18-20.
[3] 蔡俊亮等.一类幂指函数列的分析性质[J].高等数学研究,2012,4(2):10-12.
[4] 程裕强.关于型幂指函数极限的快捷方法[J].阜阳师范学院学报,2013,2(1):19-21.
[5] 韩新社.高等数学[M].合肥:中国科学技术大学出版社,2006:1-24.
[6] 邹国辉.一类幂指函数问题的探讨——以幂指函数y=xx为例[J].九江学院学报,2012,(1):121-122.
[7] 张喜善,周雪艳.幂指函数极限与导数的求法[J].山西财经大学学报,2013,4(35):169-172.
[8] 王建莉.关于幂指函数的研究[J].黑龙江科技信息,2014,28:140-144.
[责任编辑:房永磊]
Derivation of Power Exponential Function Derivate and Limit Formula
LIU Jia-bao1,YU Guo-feng2,ZHU Jia-ming3
(1. Department of Public Courses,Anhui Xinhua University,Hefei 230088,China;2. Academic Affairs
Office,Anhui Business Vocational College,Hefei 231131,China;3. Institute of statistics and applied
mathematics.Anhui university of finance and economics, Bengbu , 233030,China)
Abstract:Based on the derivation methods of general power exponent function and the derivation of y=u(x)v(x),(u(x)>0),the correct derivation method and limit formula for y=f(x)u(x)v(x),(f(x),u(x)>0)were obtained.
Key words:power exponential function,derivative formula,limit
