支持向量机核函数选择研究与仿真

2016-01-08梁礼明,钟震,陈召阳

计算机工程与科学 2015年6期

支持向量机核函数选择研究与仿真*

梁礼明，钟震，陈召阳

(江西理工大学电气工程与自动化学院，江西赣州 341000)

摘要：支持向量机是一种基于核的学习方法，核函数选取对支持向量机性能有着重要的影响，如何有效地进行核函数选择是支持向量机研究领域的一个重要问题。目前大多数核选择方法不考虑数据的分布特征，没有充分利用隐含在数据中的先验信息。为此，引入能量熵概念，借助超球体描述和核函数蕴藏的度量特征，提出一种基于样本分布能量熵的支持向量机核函数选择方法，以提高SVM学习能力和泛化能力。数值实例仿真验证表明了该方法的可行性和有效性。

关键词：支持向量机；核函数；样本分布；先验信息；能量熵

中图分类号：TP181 文献标志码：A

doi:10.3969/j.issn.1007-130X.2015.06.015

收稿日期：*2014-05-18;修回日期：2014-09-18

基金项目：国家自然科学基金资助项目(5136501)；江西省自然科学基金资助项目(20132BAB203020)；江西省教育厅科学技术研究项目(GJJ13430)

作者简介:

通信地址：341000 江西省赣州市红旗大道86号江西理工大学电气工程与自动化学院

Address:School of Electrical Engineering and Automation,Jiangxi University of Science and Technology，86 Hongqi Avenue,Ganzhou 341000,Jiangxi,P.R.China

Research and simulation of kernel function selection for support vector machine

LIANG Li-ming，ZHONG Zhen，CHEN Zhao-yang

(School of Electrical Engineering and Automation,Jiangxi University of Science and Technology,Ganzhou 341000,China)

Abstract:Support vector machine (SVM)is a kind of learning method based on kernel. Kernel function selection has significant influence on the performance of SVM, so how to effectively select the kernel function is an important problem in the field of SVM research. At present most of the kernel function selection methods neither consider the characteristics of data distribution, nor make full use of the implicit prior information in the data. We introduce a concept of energy entropy; along with the super sphere description and measurement features of kernel function, we put forth a method of kernel function selection based on the energy entropy of sample distribution so as to improve the learning ability and generalization ability of SVM. Simulations on numerical examples show that the method is feasible and effective.

Key words:SVM;kernel function；sample distribution；prior information；energy entropy

1引言

支持向量机SVM(Support Vector Machine)以统计学习理论为基础，具有完备的理论基础和严格的理论体系，能够解决有限样本的学习问题[1]。由于这一方法具有许多优良特性，如较强的模型泛化能力、不会陷入局部极小点以及很强的非线性处理能力等，因而成为近年来受到广泛关注的一类学习机器方法，在诸多领域如模式识别、回归估计、数据挖掘、生物信息等均取得了成功的应用。SVM建立在结构风险最小化原则基础之上，其核心思想之一是引入核函数技术，巧妙地解决了在高维特征空间中计算的“维数灾难”等问题。由于核函数决定了SVM的非线性处理能力，因此核函数及其参数的选择在SVM中占据着举足轻重的地位，也是SVM研究热点方向之一[2]。然而，不同的核函数所呈现出的特性各异，选择不同的核函数会导致SVM的推广性能有所不同。针对具体问题如何有效地选择(或构造)合适的核函数，是支持向量机研究领域的一个重要问题。目前，SVM核函数的选择大多是靠人工估计，根据经验进行选择，缺乏相应的理论指导，显然存在很大的随意性和局限性。因此，构建出一种能结合给定具体问题的样本数据先验信息的SVM核函数选择机制，对于SVM技术的发展和核方法的完善有着积极的指导意义。文献[3，4]基于样本数据分布特征给出了SVM训练集呈圆形、环形、球状、柱状分布的核函数测试选择方法，但实际问题中数据集的分布特征是多种多样的，需进一步改进其算法，使之具有通用性，是一个值得继续研究的内容。为此，本文引入能量熵的概念，借助超球体描述和核函数蕴藏的度量特征，提出了一种基于具体问题的样本数据分布能量熵的SVM核函数选择方法。该方法能根据样本先验信息指导选择SVM核函数，避免人为指定核函数类型，并具有直观性强、操作简便等特点，对于SVM核函数选择方法的完善以及SVM学习能力和泛化能力的提高有着积极的实用价值。

2理论基础

定理1样本数据隐含目标问题预先未知的分布特征信息。

显然，在实际的样本数据中，通常都隐含着目标问题预先未知的信息[3,4]，但大多数核选择方法都不考虑数据的分布特征，没有充分利用隐含在数据中的先验信息。

定理2不同的核函数蕴藏的几何度量特征各异，选择不同的核函数导致SVM泛化能力存在差异[5～7]。

定义1如果存在着从Rn到Hilbert空间H的变换:

(1)

使得:

其中(·)表示空间H中的内积，称定义在Rn×Rn上的函数K(x1,x2)是Rn×Rn的核函数。

下面以常用的具有局部特性的高斯径向基核函数KGauss和具有全局特性多项式核函数KPoly为例进行分析。

定义2以σ为参数的高斯径向基核函数:

(2)

是核函数。

定义3设d为正整数，则d阶齐次多项式函数

(3)

和d 阶非齐次多项式函数

(4)

都是核函数。

核函数K(x1,x2)的几何性质，由核函数的几何度量决定。如:

(1)黎曼度量：

(5)

(2)距离度量:

(6)

(3)角度度量:

cosF(x1,x2)=

(7)

则对于：

(1)高斯径向基核函数KGauss：

黎曼度量为:

(8)

距离度量为:

(9)

角度度量为:

(10)

KGauss性质表现为：

①KGauss呈现局部特性，即相互之间距离较近的数据点对核函数的值产生影响。

②所有样本数据点上的黎曼度量都是相等的。

③黎曼度量和距离度量是一致的。

④特征空间中的黎曼度量、距离度量和角度度量不会随着输入空间的正交变换和平移变换而改变。

⑤如果保持了输入空间的距离相似性，则对于输入空间中的单位向量也保持了角度的相似性。

(2)多项式核函数KPoly:

黎曼度量为：

当i=j时，

(11)

当i≠j时，

(12)

距离度量为:

(13)

角度度量为:

cosF(x1,x2)=cosd(x1,x2)

(14)

KPoly性质表现为：

①KPoly呈现全局特性，对测试点附近以及离测试点较远的整个数据点都有作用，即对单位球内的点起到减少模的作用，对单位球外的点起到扩大模的作用。

②KPoly将输入空间的原点映成特征空间的原点，且是特征空间原点的唯一原象。

③KPoly将输入空间中过原点的直线映射成特征空间中过原点的直线。当d是偶数时，映射成过原点的射线。

④特征空间的黎曼度量、距离度量和角度度量不会随着输入空间的正交变换而改变，但输入空间的平移会影响特征空间的黎曼度量、距离度量和角度度量，也就是说，特征空间的几何度量依赖输入空间的原点。

通过对KGauss和KPoly各自所蕴含的黎曼度量、距离度量和角度度量分析得知，不同的核函数会促使SVM学习能力不同，也为SVM核选择提供指导，如当需要保持输入空间的距离相似性时，选择高斯径向基核函数；当需要保持输入空间的角度相似性时，选择多项式核函数。

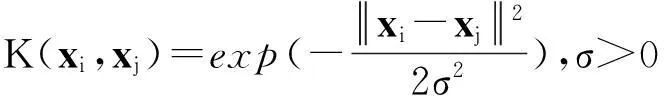
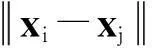
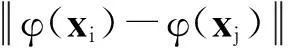
定理3表明了特征空间中的两个数据点之间的Euclidean距离仅是相应输入空间Euclidean距离的单调增加函数，这就意味着不能期望在特征空间中任意改变样本数据点之间的相互位置关系。

定理4支持向量机在L1-范数或L2-范数下平分最近点原理和最大间隔原理是等价的。

BennettKP[9]证明了上述两个原理的等价性，即它们能得到相同的最优分类超平面，并指出平分最近点原理具有更直观的几何意义，也为支持向量机的对偶问题给出了很好的几何解释。

定理5输入空间内的样本数据可视为受整个数据集的信息力作用的物理微粒，每一个微粒上的作用力是相同类或者不同类之间微粒对的作用力总和[10]。

基于距离的度量在机器学习与模式分类的诸多技术中起着重要的作用。在线性代数中，度量是定义在集合的元素之间的距离的函数。在微分几何中，度量用来定义在向量空间上的一种结构。定义合适的度量，不仅能处理欧氏距离，而且能在流形存在的情况下获得较好的效果[11]。

3算法框架

基于以上理论基础，本文提出了一种基于样本分布能量熵的支持向量机核函数选择方法。主要包括：样本数据预处理、样本数据的超球体描述、样本数据分布特征描述和分布特征判别结果四部分。

3.1样本数据预处理

3.2样本数据的超球体描述

样本数据的超球体描述的基本思想是，用以半径尽可能小的球体把样本数据全部包含起来，并以最小超球的边界作为界限对数据进行分类和描述[12～17]。

超球体描述的目标函数为:

(15)

(16)

式(15)、(16)的优化问题的解可由下面的拉格朗日函数的鞍点给出：

(17)

式(17)可转化成对偶问题:

(18)

式(18)可变成求其Wolf对偶问题的最大值：

(19)

其中，K(xi,xi)=〈φ(xi)·φ(xi)〉，K(xi,xj)=〈φ(xi)·φ(xj)〉。

式(19)为二次规划问题，通过QP优化方法得到Lagrange乘子，可确定球心和半径。

3.3样本数据分布特征描述与判别

根据设计好的超球体，接下来可以对样本数据的分布进行判别。

(20)

其中，l为样本总个数，M为能量熵Sj小于R2/4的样本数。

设定一阈值k*，当k≤k*时，则判别为样本数据呈现全局分布特性；当k>k*时，则可判别为样本数据呈现局部分布特性。对于k*的取值，本文在仿真测试的时候进行过k*取不同值的实验。k*取值偏高，会使得一些本身更倾向局部分布特征的样本数据被判为全局分布特征；k*取值偏低，会使得一些本身更倾向全局分布特征的样本数据被判为局部分布特征，从而不能正确地选择核函数。综合考虑，选择k*的值为0.5，这样能较准确地进行样本分布特征的判别。经过仿真验证，实验结果与判别结果是一致的。

3.4SVM核函数选择机制

根据样本分布特征判别函数所得样本分布特性，结合核函数所蕴藏的度量特性选择SVM核函数类型。由此可以建立一个核函数选择机制：当k>k*时，则选取高斯径向基核函数KGauss；当k≤k*时，则选取多项式核函数KPoly。

4实例仿真与分析

本文算法流程如图1所示。实验仿真所用的数据均来自UCI数据库，且为带标签的数据。SVM分类采用的是台湾大学林智仁(Lin Chih-Jen)教授等开发设计的LIBSVM工具箱。本次仿真的实验环境为运用软件Matlab R2009a，运行于Intel Pentium/2.79 GHz、2 GB内存的PC。本实验中取阈值k*=0.5，并随机选取每组样本数据的80%作为训练集，其余20%用作测试集。

Figure 1　Flow chart of SVM kernel function choice method 图1　支持向量机核函数选择方法流程图

4.1实验仿真

4.1.1样本数据分布特征判别

本文从UCI数据库中随机选取六组数据进行实验仿真。首先对样本进行预处理，使其范数小于1，防止维数灾难；然后对其进行超球体描述，根据式(19)计算其球心及半径；最后样本数据分布特征判别，根据构建的样本分布判别函数式(20)计算k，再根据已设定的阈值k*判别各样本数据分布特征。各数据集的规模、球心坐标、半径及分布判别结果如表1所示。

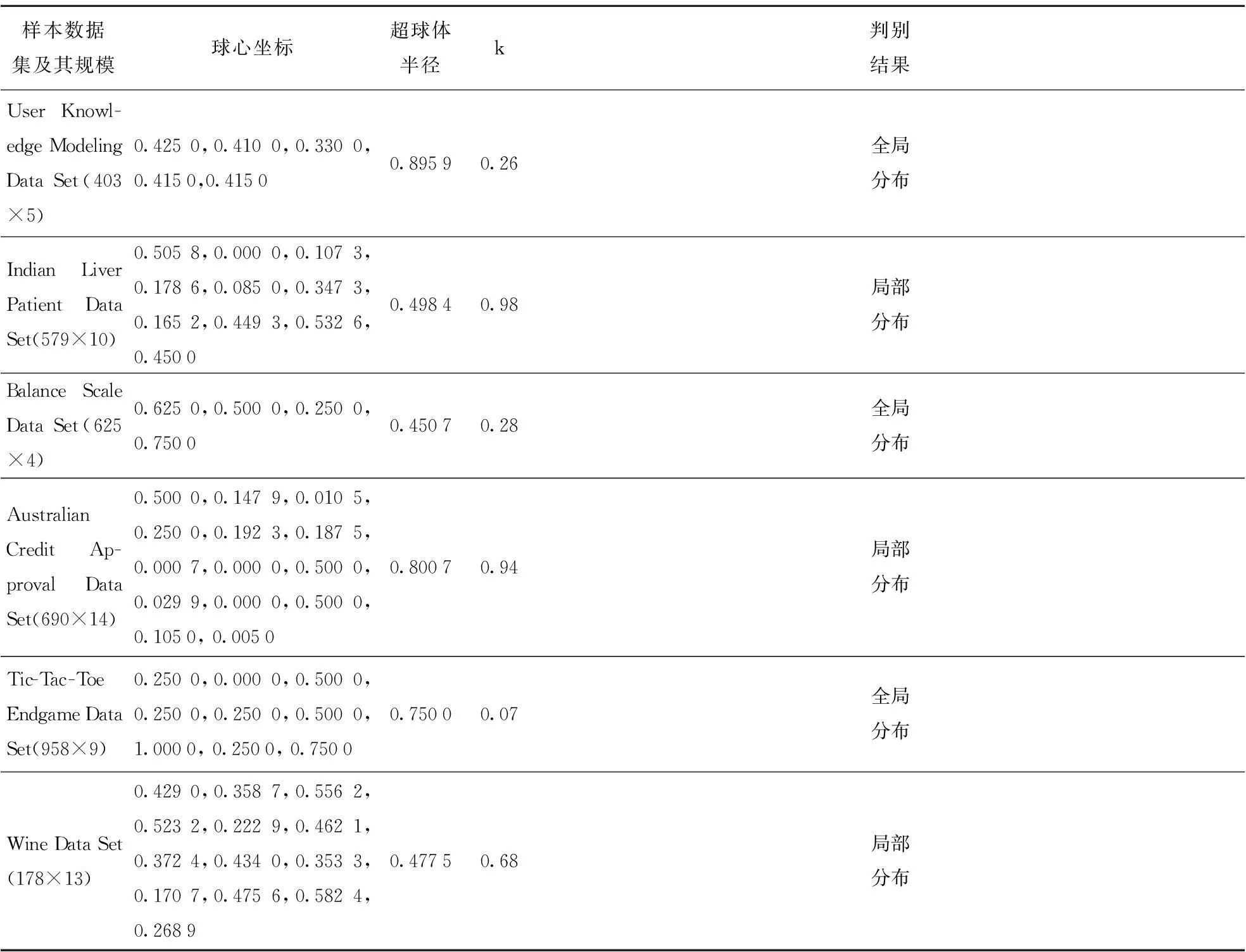
Table 1　Sample data distribution

4.1.2样本数据仿真测试

运用具有全局特性的多项式核函数和局部特性的RBF径向基核函数，对以上六组样本数据分布特征判别结果进行测试验证。六组实例中，每组随机进行三次训练集、测试集的选取，测其分类效果，计算每组数据各核函数分类效果平均值。实例中SVM模型参数优化均采取粒子群算法进行寻优，各样本数据分类测试结果以及实验时间如表2所示。

从表1、表2中可以得出结论：

(1)采用建议优先选择的核函数类型所得的分类正确率要优于不建议采用的核函数类型，其差异程度甚至高达10%之多。究其原因有三：一是每组样本数据都隐含着不尽相同的统计分布特征；二是不同的核函数几何度量特征表现各异；三是SVM分类效果的好坏取决于特征空间中的样本之间的Euclidean距离，而样本点在特征空间中的Euclidean距离与其相应输入空间Euclidean距离紧密相关。因此，在实际应用中需充分挖掘隐含在样本数据中的先验信息，然后结合核函数各自的度量特征选择(或构造)合适的核函数，以促进SVM泛化能力最大化。

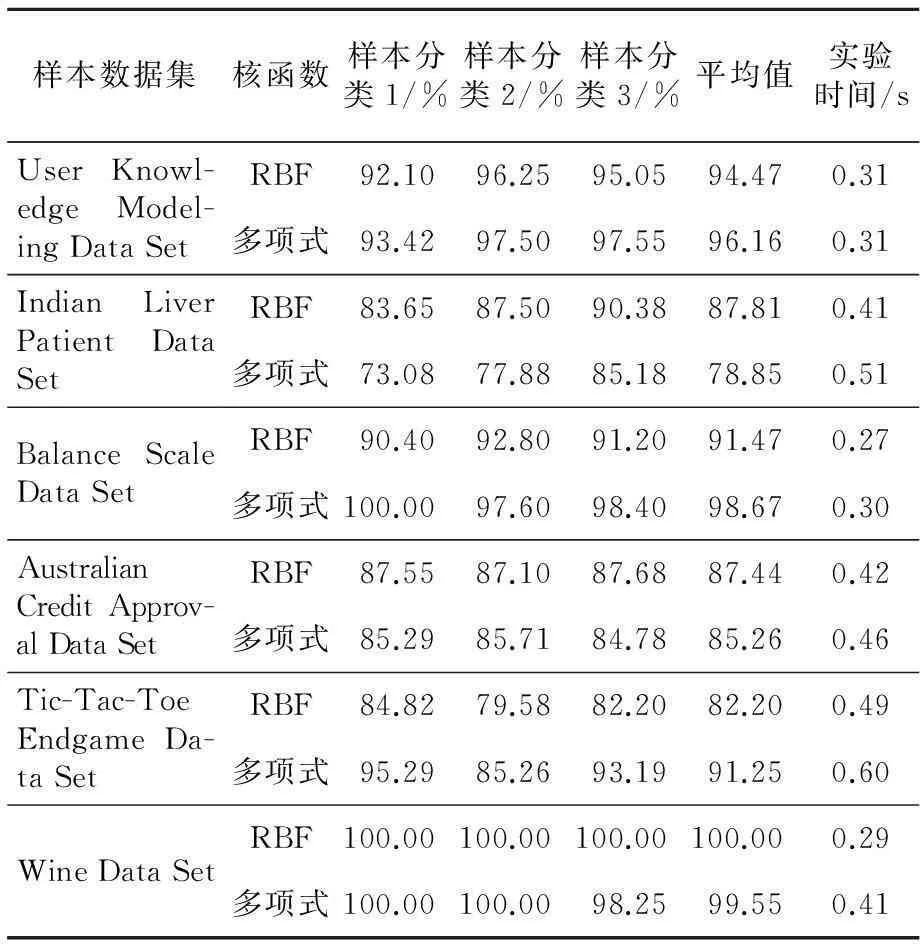
Table 2　Sample data simulation tests

(2)从上述仿真实例结果来看，本文提出的基于样本与超球体球心欧氏距离度量的能量熵分布判别函数能较好地表征样本统计分布特征，为后续的SVM核函数选择奠定基础。

(3)具有全局特性的多项式核函数和局部特性的径向基核函数的SVM预测算法运行时间相当且耗时少，实时性较好，多项式核函数运行时间略长于径向基核函数。

(4)对于一个具有l个样本的训练集，求解SVM的QP问题的时间复杂度为O(l3)、空间复杂度为O(l2)。本文所提出的基于样本分布能量熵的信息判别需要进行l(l+1)/2次比较，因此，基于样本分布能量熵的SVM核函数选择算法时间复杂度为O(l3+(l+1)/2)，仍为多项式级。从算法复杂度角度考虑，本文提出的算法是合理的。

4.2样本数据对比分析

本文随机选取其他文献[12,18]中所用的数据进行仿真测试对比，数据集有Australian Credit Approval Data Set、Breast Cancer Wisconsin (Original) Data Set、Statlog (Heart) Data Set、Car Evaluation Database四组。经过样本数据分布的判别，三组样本数据均呈局部分布特性。分类测试结果平均值与文献[12,18]的对比如表3所示。

Table 3　Classification Comparison of the same set of

注：表中“1”为其他文献结果，“2”为本文结果。

通过四组实例仿真与对比可以看出，前三组其他文献在相同数据的分类结果要低于应用本文方法的分类测试结果。数据集Breast Cancer Wisconsin(Original)Data Set中，本文实验的两种核函数分类结果差值要优于其他文献。数据Australian Credit Approval Data Set和Statlog (Heart) Data Set数据呈局部分布，但其他文献的分类结果RBF核函数要低于多项式核函数，而在本文实验中，RBF核函数要优于多项式核函数。其他文献的RBF核函数可以达到一个更好的分类结果。

第四组数据集Car Evaluation Database中数据呈全局分布。文献[18]中多项式核函数的分类结果却明显低于RBF核函数的分类结果，本文所做的相同数据分类测试多项式优于其RBF分类结果，所以其并没有充分发挥多项式核函数的性能，没有选择针对该数据性能更加优的核函数。

5结束语

以上介绍SVM核函数选择方法运用样本数据蕴含的先验信息，结合核函数的度量特征，引入能量熵概念，借助超球体描述提出一种基于样本数据分布特征核函数选择方法。这种基于样本数据分布特征核函数选择方法，是一种有指导性的SVM核函数选择实用方法，克服了传统的SVM模型选择方法中人为指定核函数类型而导致模型不能达到最优性能的缺点，并具有运算速度快、非常适合实时在线SVM模型预测控制场所等特点。通过相应的实例仿真验证，表明了该方法的可行性和有效性，丰富了核函数选择方法，有助于SVM学习能力和泛化能力的提高，具有一定的推广价值。此外，在实际工程问题中，数据集的分布是极其丰富的，有时用单一核函数难以准确刻画其分布特征，如在本文的基础上增加或改进核函数选择形式，如组合核函数，使之描述更加全面，将是本文下一步研究的延伸方向。

参考文献:

[1]Deng Nai-yang,Tian Ying-jie.Support vector machine theory,algorithm and expand[M].Beijing:Science Press,2009.(in Chinese)

[2]Ding Shi-fei,Qi Bing-juan,Tan Hong-yan.An overview on theory and algorithm of support vector machines[J].Journal of University of Electronic Science and Technology of China,2011,40(1):2-10.(in Chinese)

[3]Tao Jian-wen,Wang Shi-tong.Local learning based support vector machine[J].Control and Decision,2012,27(10):1510-1515.(in Chinese)

[4]Liang Li-ming,Feng Xin-gang,Chen Yun-nen,et al.Method of selection kernel function based on distribution characteristics of samples[J].Computer Simulation,2013,30(1):323-328.(in Chinese)

[5]Luo Lin-kai,Ye Ling-jun,Zhou Qi-feng.Geometric measures and properties of commonly used kernel functions[J].Journal of Xiamen University,2009,48(6):804-807.(in Chinese)

[6]Thierman J S,Hallaj I M. Apparatus and method for geometric measurement:U.S. Patent Application 12/784,694[P]. 2010-05-21.

[7]Sohelf A,Karmakar G C,Dooleyls S,et al.Geometric distortion measurement for shape coding:A contemporary review[J].ACM Computing Surveys(CSUR),2011,43(4):29.

[8]Wang Ting-hua.Research on model selection for support vector machine[D].Beijing:Beijing JiaoTong University,2009.(in Chinese)

[9]Bennett K P,Bredensteiner J.Duality and geometry in SVM classifiers[C]//Proc of the 17th International Conference on Machine Learning,2000:5764.

[10]Kevi N,Zhou S,Chellappa R.From sample similarity:Probabilistic distance measure in reproducing kernel hilbert space[J].IEEE Transactions on Pattern and Machine Analysis Intelligence,2006,28(6):917-929.

[11]Liu Song-hua.Low-rank decomposition of kernel matrix and informative energy metric in kernel space[D].Xi’an:Xidian University,2011.(in Chinese)

[12]Luo Lin-kai.Research on kernel selection of support vector machine[D].Xiamen:Xiamen University,2007.(in Chinese)

[13]Zhao Feng,Zhang,Jun-ying,Liu Jing.An optimizing kernel algorithm for improving the performance of spport vector domain description[J].Acta Automatica Sinica,2008,34(9):1122-1127.(in Chinese)

[14]Xu Tu,Luo Yu,He Da-ke.SMO trainning algorithm for hypersphere one-class SVM[J].Computer Science,2008,35(6):178-180.(in Chinese)

[15]Li Yu,Zheng Min-juan,Cheng Guo-jian.Research on classification method based on support vector data description[J].Computer Engineering,2009，35(1)：235-236.(in Chinese)

[16]Zhang Hui-min,Chai Yi.Non-equidistant margin hypersphere SVM[J].Computer Engineering and Application,2011，47(11)： 19-22.(in Chinese)

[17]Wen Chuan-jun,Zhan Yong-zhao,Chen Chang-jun.Maximal-margin minimal-volume hypersphere suppot vector machine[J].Control and Decision,2010,25(1):79-83.(in Chinese)

[18]Song Hui,Xue Yun,Zhang Liang-jun.Research on kernel function selection simulation based on SVM[J].Computer and Modernization,2011(8):133-136.(in Chinese)

参考文献：附中文

[1]邓乃扬,田英杰. 支持向量机—理论、算法与拓展[M]. 北京:科学出版社,2009.

[2]丁世飞,齐丙娟,谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报，2011,40(1):2-10.

[3]陶剑文,王士同. 局部学习支持向量机[J]. 控制与决策,2012,27(10):1510-1515.

[4]梁礼明,冯新刚,陈云嫩,等. 基于样本分布特征的核函数选择方法研究[J]. 计算机仿真,2013,30(1):323-328.

[5]罗林开,叶凌君,周绮凤. 常用核函数的几何度量与几何性质[J]. 厦门大学学报,2009，48(6):804-807.

[8]汪廷华. 支持向量机模型选择研究[D]. 北京：北京交通大学,2009.

[11]刘松华. 核矩阵低秩分解与核空间信息能度研究及应用[D]. 西安：西安电子科技大学,2011.

[12]罗林开.支持向量机的核选择[D].厦门：厦门大学，2007.

[13]赵峰,张军英,刘敬. 一种改善支撑向量域描述性能的核优化算法[J]. 自动化学报,2008,34(9):1122-1127.

[14]徐图,罗瑜,何大可. 超球体单类支持向量机的SMO训练算法[J]. 计算机科学,2008,35(6):178-180.

[15]李瑜,郑敏娟,程国建. 基于支持向量数据描述的分类方法研究[J]. 计算机工程,2009，35(1)：235-236.