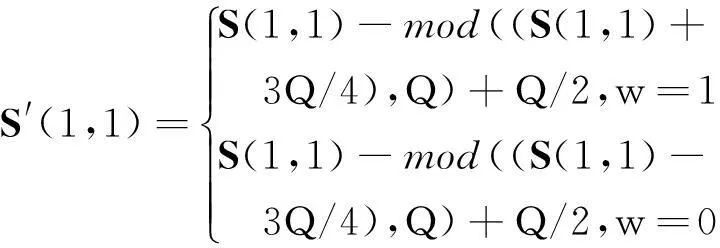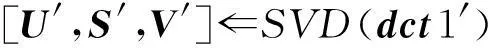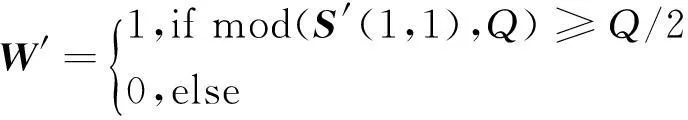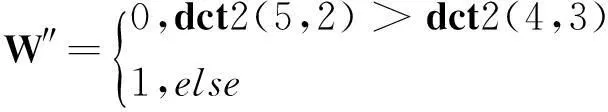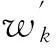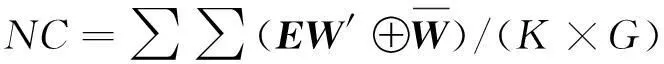基于3D-DCT和SVD的鲁棒彩色图像水印算法

基于3D-DCT和SVD的鲁棒彩色图像水印算法*

熊祥光，韦立，谢刚

(贵州师范大学数学与计算机科学学院，贵州 贵阳 550001)

摘要：在数字图像水印领域，水印算法主要集中于灰度图像，且提出的大部分彩色图像水印算法往往仅在亮度分量或在彩色图像的每一通道中嵌入水印，未能充分利用彩色图像的冗余空间，影响了水印的透明性和鲁棒性。针对此问题，提出了一种新颖的基于三维离散余弦变换和奇异值分解的彩色图像水印算法。算法先对水印图像进行预处理和对彩色图像进行互不重叠的分块；其次对每一分块进行三维离散余弦变换；最后选择对三维离散余弦变换系数的第一分量进行奇异值分解。嵌入水印时，对三维离散余弦变换系数第一分量的最大奇异值和第二分量分别采用量化和关系的嵌入方法嵌入水印。提取水印时，分别采用量化和关系提取算法提取水印并进行比较，选取相似值高的水印图像作为最终提取的水印。实验结果表明，提出的算法具有较好透明性的同时，具有抵抗常规信号处理和模糊、扭曲及锐化等攻击的能力。

关键词：彩色图像水印；三维离散余弦变换；奇异值分解；关系；量化；鲁棒性

中图分类号：TP391.41 文献标志码：A

doi:10.3969/j.issn.1007-130X.2015.06.010

收稿日期：*2014-05-15;修回日期：2014-08-11

基金项目：国家自然科学基金资助项目(61309006);贵州省科学技术厅、贵州师范大学联合科技基金资助项目(黔科合LH字[2014]7041号)

作者简介:

通信地址：550001 贵州省贵阳市贵州师范大学数学与计算机科学学院

Address:School of Mathematics and Computer Science,Guizhou Normal University,Guiyang 550001,Guizhou,P.R.China

A robust color image watermarking algorithm based on 3D-DCT and SVD

XIONG Xiang-guang,WEI Li,XIE Gang

(School of Mathematics and Computer Science,Guizhou Normal University,Guiyang 550001,China)

Abstract:In the field of digital image watermarking, watermarking algorithms mainly focus on gray images, whereas most of color images watermarking algorithms usually embed watermarking only in the luminance component or in each channel of color image separately. These algorithms are unable to make full use of the redundant space of color images, thus affecting the watermarking’s transparency and robustness. To solve these problems,we propose a novel color image watermarking algorithm based on the three-dimensional discrete cosine transform (3D-DCT) and the singular value decomposition (SVD). Firstly, the watermarking image is pre-processed and the color image is subdivided to non-overlapping blocks.Secondly, we perform the 3D-DCT for each block and apply the SVD in the first component of the 3D-DCT coefficients. We use the quantization method and the relationship method to embed watermarking in the largest singular value and the second component of 3D-DCT coefficients respectively at the embedding watermarking stage.At the watermarking extraction stage, we extract the watermarking image using the quantization method and the relationship method separately and the results are compared. The result with higher correlation value is chosen as the final extracted watermarking. Experimental results show that the proposed algorithm has good transparency and the ability to resist common signal processing and fuzzy, distorted, sharpening attacks.

Key words:color image watermarking;three-dimensional discrete cosine transform;singular value de-composition;relationship;quantization;robustness

1引言

随着网络技术和多媒体技术的飞速发展，数字水印技术己成为多媒体领域的研究热点。当前在图像水印领域，绝大多数的水印算法都是在灰度图像中嵌入水印，即使原始的载体图像是彩色的，往往也是先对其进行色彩空间的变换，再在亮度分量或在彩色图像的每一通道或某一通道中嵌入水印信号。

文献[1]使用主成分分析技术对调色板中的颜色进行排序，得到奇、偶索引两个调色板，根据嵌入的水印取值与颜色索引的奇偶性嵌入水印。文献[2]分别在RGB彩色图像的每一通道中采用关系的方法嵌入水印信号。文献[3]利用发送分集技术的思想，将经过预处理后的水印嵌入到彩色图像的红、绿和蓝通道中。文献[4]先对彩色图像的每一通道进行离散余弦变换，再采取“加性”的嵌入策略在每一个通道中嵌入水印。文献[5，6]选择在彩色图像绿色分量中嵌入水印。文献[7]先利用扩频技术将水印信号生成体水印信号，再对体水印信号和载体数据分别进行分块三维离散余弦变换，采用“加性”的嵌入方法嵌入水印。实验表明，该算法具有较好的透明性和鲁棒性，但是该算法由于在提取水印时需要原始的体数据，使该算法的适用范围受到一定的限制。文献[8]先分别对每一分块的红、绿和蓝通道进行提升小波变换和对低频子带进行离散余弦变换，再将水印自适应嵌入到直流系数中。文献[9,10]提出基于三维离散余弦变换的视频水印算法，实验表明这两种算法都具有较好的透明性和鲁棒性。

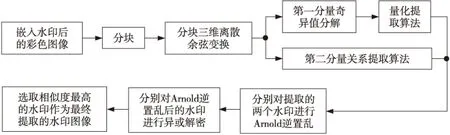
从上述文献可以看出，大部分的彩色图像水印算法都是在彩色图像的每一个通道或某一通道中嵌入水印，未能充分利用彩色图像的冗余空间，导致水印的透明性和抵抗攻击的能力不佳。为此，结合三维离散余弦变换和奇异值分解的优点，提出一种新颖的彩色图像水印算法。在嵌入水印阶段，先对水印信号进行预处理和对载体图像进行分块；其次对每一分块进行三维离散余弦变换和对三维离散余弦变换系数的第一分量进行奇异值分解；最后对奇异值分解后的最大奇异值和三维离散余弦变换后的第二分量分别采用量化和关系的嵌入策略嵌入预处理后的水印。在提取水印阶段，先分别使用量化和关系的提取策略在相应的嵌入位置提取水印；其次对提取的水印进行Arnold逆置乱和异或运算得到解密后的水印；最后通过计算提取的水印图像与原始水印图像的相似性，选取相似值高的图像作为最终提取的水印图像。实验结果表明，该算法不仅具有较好的透明性，而且对多种攻击也具有较强的鲁棒性，具有一定的应用价值。

2三维离散余弦变换及逆变换

设三维数据块V的大小分别为nx、ny、nz，f(x,y,z)表示三维数据块V在(x,y,z)处的数据值，F(a,b,c)表示该三维数据块对应的三维离散余弦变换系数，则三维离散余弦变换的计算公式如下[11]：

(1)

其中，

相应地三维离散余弦逆变换的计算公式如下[11]：

(2)

其中，C(a)、C(b)和C(c)的意义与三维离散余弦变换公式(1)中的相同。

3提出的彩色图像水印算法

3.1水印图像的预处理

为了增强水印的安全性，在嵌入水印之前，先对水印进行异或加密和Arnold置乱，详细的加密和置乱过程如下。

(1)选取初始值x0，利用logistic混沌映射产生混沌序列xk。

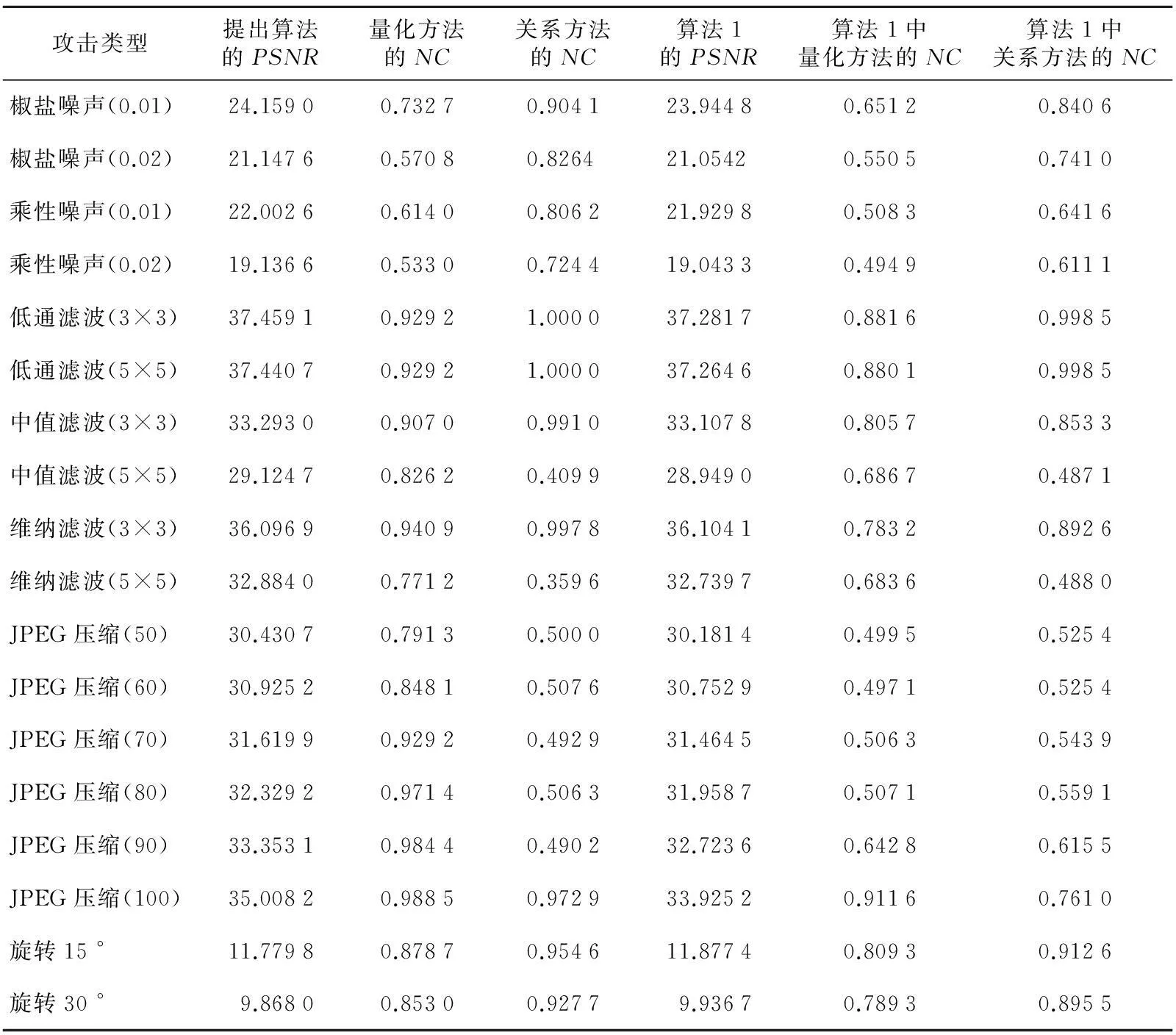
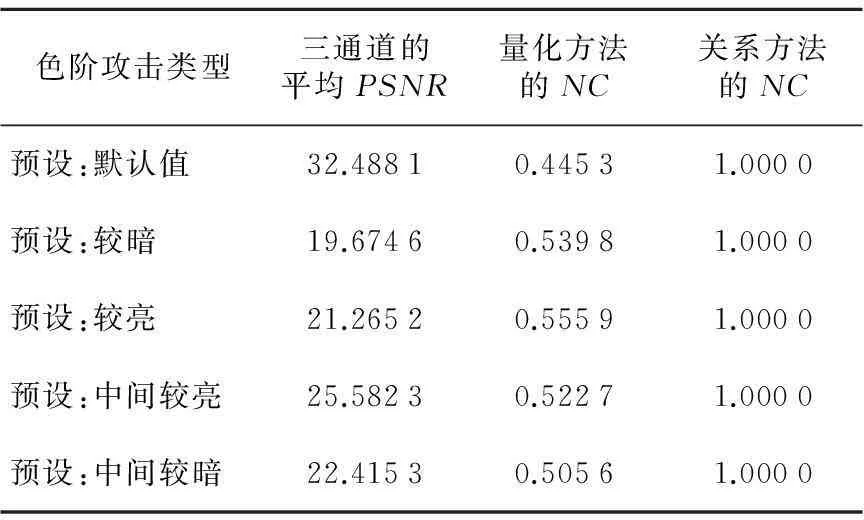
(3)

其中，k=0,1,2,…;0

(4)

(5)

其中，符号⊕表示异或运算。

(4)将异或加密后的一维序列pk转换为二维，再选定迭代次数t对其进行Arnold置乱，得到待嵌入的二值水印信号。

解密算法与加密算法过程基本相同。在进行解密时，应先进行Arnold逆置乱，再进行异或运算。另外，需要知道混沌序列的初始值x0和Arnold置乱的迭代次数t，否则不能正确地恢复嵌入的二值水印信号。

Figure 2　Watermarking embedding process 图2　水印嵌入过程

对大小为64×64标识 “贵州师大”的二值图像采用上面的方法进行异或加密和Arnold置乱处理，得到一幅杂乱无章的图像，如图1所示。图1c和图1d分别是迭代次数t正确时，初始值x0=0.123和初始值x0=0.123 001时恢复的图像。从图1c和图1d可见，即使初始值仅相差0.000 001，也不能正确地恢复原始的二值图像，从而增强了图像的安全性。若还想进一步提高图像的安全性，可采用AES(AdvancedEncryptionStandard)或其他加密算法对二值图像的像素进行加密后，再进行Arnold置乱。

Figure 1　Encryption and decryption of the binary images 图1　二值图像的加密和解密

3.2水印嵌入算法

水印嵌入过程如图2所示。

水印嵌入算法的详细步骤如下：

(1)水印图像的预处理。采用3.1节的加密和置乱方法对二值水印图像W进行预处理，得到异或加密和Arnold置乱后的二值水印图像。嵌入水印时，实际使用的是预处理后的水印图像。

(2)载体图像分块。设RGB彩色图像I每一分量的大小为M×M，分块的大小为8×8，则对三维的RGB彩色图像进行互不重叠的分块后，每一分块B的大小为8×8×3，可将载体图像分成(M×M)/(8×8)块。

(3)分块三维离散余弦变换。采用公式(1)对每一分块B进行三维离散余弦变换，得到三维的离散余弦变换系数DCT。

DCT⟸3D-DCT(B)

(6)

其中，3D-DCT(·)表示对分块B进行三维离散余弦变换。

(4)分块奇异值分解。选择分块三维离散余弦变换系数DCT的第一分量DCT(:,:,1)，设为dct1,并对其进行奇异值分解[12]。

[U,S,V]⟸SVD (dct1)

(7)

其中，SVD(·)表示奇异值分解，U和V分别表示奇异值分解后的两个正交矩阵，S表示对角矩阵。

(5)采用量化嵌入方法嵌入第一个水印。设奇异值矩阵Si的第一个系数为Si(1,1)，采用公式(8)嵌入预处理后的二值水印图像。

(8)

其中，S′(1,1)表示嵌入水印后的系数，w表示一位二值水印位，Q表示水印嵌入强度，影响水印的透明性和鲁棒性，符号mod(·)表示取模运算。

(6)分块逆奇异值分解。先将嵌入水印后的奇异值S′(1,1)替换S(1,1)，再将步骤(4)奇异值分解生成的两正交矩阵U和V与矩阵S进行逆奇异值分解，得到嵌入水印后的第一分量。

dct1⟸U*S*(V)T

(9)

其中,符号*表示矩阵的乘法运算，上标T表示矩阵的转置运算。

(7)采用关系嵌入方法嵌入第二个水印。选择分块三维离散余弦变换系数DCT的第二分量，设为dct2。对于8×8的系数块，选择调整位置为(4，3)和(5，2)的系数的大小关系嵌入水印(也可以选择其他位置的系数对嵌入水印)，详细的嵌入算法如下：

Figure 3　Watermarking extraction process 图3　水印提取过程

ifw=0 // 待嵌入的一位水印

if(dct2(5,2)

dct2(5,2)⟺dct2(4,3) // 交换两个系数

end

else

if(dct2(5,2)>dct2(4,3))

dct2(5,2)⟺dct2(4,3) // 交换两个系数

end

end

if(dct2(5,2)>dct2(4,3))

if(dct2(5,2)-dct2(4,3)

dct2(5,2)=dct2(5,2)+K/2

dct2(4,3)=dct2(4,3)-K/2

(10)

end

else

if(dct2(4,3)-dct2(5,2)

dct2(4,3)=dct2(4,3)+K/2

dct2(5,2)=dct2(5,2)-K/2

(11)

end

end

其中,K为预定义的阈值，影响水印的透明性和鲁棒性，本文选取K的值为20。为了增强嵌入水印的透明性和鲁棒性，还可根据载体图像的特性自适应选取。

(8)对每一分块调整后的系数进行三维离散余弦逆变换，得到含水印的分块B′。

B′⟸3D-IDCT(DCT)

(12)

其中，3D-IDCT(·)表示进行三维离散余弦逆变换。

(9)重复步骤(3)～(8)，直到所有的水印信号嵌入完毕后，得到最终含水印的彩色图像I′。

3.3水印提取算法

该算法的水印提取过程非常简单，不需要原始载体彩色图像和原始水印图像的参与，是一种盲水印算法。水印提取过程如图3所示。

水印提取算法的详细步骤如下：

(1)含水印图像分块。根据嵌入时分块的大小，对大小为M×M的含水印RGB彩色图像I′(可能已受到有意或无意的攻击处理)进行互不重叠的8×8分块，得到(M×M)/(8×8)个子块。

(2)分块三维离散余弦变换。采用公式(1)对每一分块B′进行三维离散余弦变换，得到三维的离散余弦变换系数DCT′。

DCT′⟸3D-DCT(B′)

(13)

(3)分块奇异值分解。选择分块三维离散余弦变换系数DCT′的第一分量dct1′，并对其进行奇异值分解。

(14)

(4)采用量化提取方法提取第一个水印。设奇异值矩阵S′的第一个系数为S′(1,1)，采用公式(15)提取第一个未解密和未逆Arnold置乱的二值水印图像W′。

(15)

(5)采用关系提取方法提取第二个水印。选择分块三维离散余弦变换系数DCT′的第二分量dct2，采用如下的规则提取第二个未解密和未逆Arnold置乱的二值水印图像W″。

(16)

(9)采用归一化互相关系数NC(NormalizeCorrelation)来客观评价提取的水印与原始水印的相似性，NC值越高，表明提取的水印失真越小，与原始的水印图像越相似。NC的计算公式如下：

(17)

(10)利用公式(17)分别对提取的二值水印图像EW′和EW″计算与原始二值水印图像的相似值，选取相似值最高的二值水印图像作为最终提取的水印图像。

4仿真实验结果

4.1透明性测试

提出的算法在Windows 7和Matlab 2007b平台下进行仿真实验，量化嵌入方法的嵌入强度Q取值为60，关系嵌入方法的嵌入强度T为20。载体图像为两幅大小为512×512的真彩色标准Airplane和Sailboat图像(图4中已将彩色图像转换为灰度图像)，分别如图4a和图4b所示。水印图像大小为64×64标识“贵州师大”的二值图像，如图4c所示。图4d和图4e是嵌入水印后的图像，图4f是从含水印的Airplane图像提取的图像。从提取的水印图像可见，当含水印的彩色图像未受到任何的攻击时，能完整地提取嵌入的二值水印图像。

Figure 4　Experimental results of transparency 图4　透明性实验结果

采用峰值信噪比PSNR(Peak Signal to Noise Ratio)来客观评判含水印的图像与原始图像的差别，PSNR值越大，表明水印的不可感知性就越好。PSNR的计算公式如下：

(18)

其中，M和N分别表示载体图像的长和宽，I和I′分别表示原始图像和嵌入水印后的图像,Imax表示原始图像像素的最大值。

为了验证算法的不可感知性，在彩色图像R分量离散余弦变换的直流系数中和位置为(4，3)与(5，2)的系数中分别采用量化和关系的嵌入方法嵌入水印(以下简称算法1)。相同条件下，实验结果如表1所示。从图4和表1可以看出，嵌入水印后的彩色图像满足不可感知性的要求。与算法1相比，提出的算法具有更好的透明性。

Table 1　Experimental results of transparency

4.2抗常规信号处理能力测试

对含水印的两幅彩色图像分别进行多种常规信号处理攻击实验，都具有较好的鲁棒性。限于篇幅，下面以嵌入水印后的Airplane彩色图像为例，进行诸如滤波、JPEG压缩(品质百分数分别为50，60，…，100)、旋转(先顺时针旋转x°，再逆时针旋转x°)等多种攻击实验，实验结果如表2所示。从表2可见，对于大部分的攻击，关系嵌入算法比量化嵌入算法的鲁棒性更强，但对于JPEG压缩攻击，量化嵌入算法的鲁棒性强于关系嵌入算法。在PSNR基本相当的条件下，该算法抵抗常规信号处理的能力明显强于算法1。

4.3抗Adobe Photoshop能力测试

Adobe Photoshop作为一款专业的图像编辑

Table 2　Experimental results against common signal processing attacks

软件，大部分的图像往往需要经过Adobe Photoshop软件的处理，因此嵌入水印后的图像应该也要能抵抗这种处理。实验中，选择Adobe Photoshop CS4软件先对含水印的图像进行诸如亮度与对比度调整、色阶、曲线、曝光度、滤镜、模糊、扭曲及锐化等处理，然后在处理后的图像中提取水印，实验结果如表3～表7所示。从实验结果可以看出，基于量化的嵌入算法抵抗该类处理的能力较弱，但基于关系的嵌入算法具有较强的抵抗该类攻击的能力。

Table 3　Experimental results

Table 4　Experimental results against level attacks

Table 5　Experimental results against curve attacks

Table 6　Experimental results against

Table 7　Experimental results against

4.4与文献[2]算法的比较

文献[2]采用关系的嵌入方法分别在RGB彩色图像的每一通道中嵌入水印信号。为了与该算法具有可比性，相同条件下，调整嵌入强度，使采用两种方法嵌入的图像的PSNR值大体相当(该算法的平均PSNR为42.852 3，文献[2]的平均PSNR为42.464 8)，相应的实验结果如表8所示(提出的算法和文献[2]中的算法都是选择最好的NC值)。从表8可以看出，提出的算法具有更优越的性能。

5结束语

结合三维离散余弦变换和奇异值分解的优点，提出了一种基于三维离散余弦变换和奇异值分解

Table 8　Performance comparison with reference [2]

的与常见彩色图像水印方案不同的水印算法。该算法未进行色彩空间的转换和未在彩色图像的每一通道或某一通道中嵌入水印，而是将彩色图像当作体数据进行分块的三维离散余弦变换。嵌入水印时，对三维离散余弦变换系数第一分量的最大奇异值和第二分量分别采用量化和关系的嵌入策略嵌入水印。提取水印时，先提取两个水印图像并分别计算与原始水印图像的相似性，选取相似值高的水印图像作为最终提取的水印。仿真实验表明，该算法具有较好的透明性，基于量化的嵌入方法抵抗JPEG压缩的能力较好，但抵抗其他攻击的能力比基于关系的嵌入方法的抗攻击能力弱。与采用同样的嵌入方法在单通道中嵌入水印相比，该算法能充分利用体数据的冗余空间，具有更优越的透明性和鲁棒性。由于提出的算法选取相似值高的图像作为最终提取的水印图像，因此该算法具有抵抗多种攻击的能力，对彩色图像的版权保护具有一定的应用价值。

参考文献:

[1]Piyu T, Hu Yu-chen, Chang Chin-chen. A color image watermarking scheme based on color quantization[J]. Signal Processing, 2004, 84(1):95-106.

[2]Xiong Xiang-guang, Wang Duan-li. Color image watermarking scheme based on HVS and coefficient in DCT domain [J]. Computer Engineering & Science, 2014, 36(2):311-316.(in Chinese)

[3]Li Xiao-qiang, Xue Xiang-yang. Multi-channel based watermarking scheme for color image[J]. Chinese Journal of Computer, 2004, 27(9):1238-1244.(in Chinese)

[4]Bami M, Bartolim F, Piva A. Multichannel watermarking of color images[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2002, 12(3):142-156.

[5]Liu Lian-shan, Li Ren-hou, Gao Qi. DWT-based color image watermarking scheme of embedding watermarking into the green components[J]. Journal on Communications, 2005, 26(7):62-67.(in Chinese)

[6]Guo Qiao-dan,Wu Xi-sheng.A blind watermarking algorithm of color image based on SVD[J]. Computer Engineering & Science, 2012, 34(11):109-113.(in Chinese)

[7]Liu Wang,Jiang Shou-da,Sun Sheng-he.Robust watermarking for volume data based on 3D-DCT[J]. Acta Electronica Sinica, 2005, 33(12):2174-2177. (in Chinese)

[8]Xiong Xiang-guang,Wang Li,Wang Duan-li.Color video watermarking algorithm based on lifting wavelet transform and DCT[J]. Application Research of Computer, 2013, 30(4):1191-1193.(in Chinese)

[9]Hui Y H, Cheng H Y, Wen H H. A video watermarking technique based on pseudo-3D DCT and quantization index modulation[J]. IEEE Transactions on Information Forensics and Security, 2010, 5(4):625-637.

[10]Narendra K S,Chetan K R,Shivanandr D.A 3D-DCT based robust and perceptual video watermarking scheme for variable-temporal length video sequence[J].World Journal of Science and Technology, 2012, 2(10):65-69.

[11]Rao K, Yip R. Discrete cosine transform:Algorithms, advantages, applications[M]. Boston:Academic Press Inc, 1990.

[12]Liu R, Tan T. An SVD-based watermarking scheme for protecting rightful ownership [J]. IEEE Transactions on Multimedia, 2002, 4(1):121-128.

参考文献：附中文

[2]熊祥光, 王端理. 基于HVS和关系的DCT域彩色图像水印方案[J].计算机工程与科学, 2014, 36(2):311-316.

[3]李晓强, 薛向阳. 基于多通道的彩色图像水印方案[J].计算机学报，2004, 27(9):1238-1244.

[5]刘连山, 李人厚, 高琦.基于DWT的彩色图像绿色分量数字水印方案[J].通信学报，2005, 26(7):62-67.

[6]郭巧丹, 吴锡生. 基于SVD的彩色图像盲水印算法[J].计算机工程与科学, 2012, 34(11):109-113.

[7]刘旺, 姜守达, 孙圣和.基于三维DCT变换的体数据鲁棒数字水印嵌入算法[J].电子学报, 2005, 33(12):2174-2177.

[8]熊祥光, 王力, 王端理. 基于提升小波变换和DCT的彩色视频水印算法[J].计算机应用研究, 2013, 30(4):1191-1193.

熊祥光(1984-),男,贵州织金人，硕士，讲师，CCF会员(E200022762M)，研究方向为数字水印和图像处理。E-mail:xxg0851@163.com

XIONG Xiang-guang,born in 1984,MS,lecturer,CCF member(E200022762M)，his research interests include digital watermarking, and image processing.

韦立(1981-),男,广西都安人，博士，研究方向为可计算性与计算复杂性。E-mail:weilikb@163.com

WEI Li,born in 1981,PhD,his research interests include computability, and computational complexity.

谢刚(1980-),男,贵州六盘水人，博士，副教授，研究方向为软件工程。E-mail:48263091@qq.com

XIE Gang,born in 1980,PhD,associate professor,his research interest includes software engineering.