一种新的有监督的局部保持典型相关分析算法
2016-01-08潘荣华,陈秀宏,曹翔
一种新的有监督的局部保持典型相关分析算法*
潘荣华,陈秀宏,曹翔
(江南大学数字媒体学院,江苏 无锡 214122)
摘要:从模式识别的角度出发,在局部保持典型相关分析的基础上,提出一种有监督的局部保持典型相关分析算法(SALPCCA)。该方法在构造样本近邻图时将样本的类别信息考虑在内, 由样本间的距离度量确定权重,建立样本间的多重权重相关,通过使同类内的成对样本及其近邻间的权重相关性最大,从而能够在利用样本的类别信息的同时,也能保持数据的局部结构信息。此外,为了能够更好地提取样本的非线性信息,将特征集映射到核特征空间,又提出一种核化的SALPCCA(KSALPCCA)算法。在ORL、Yale、AR等人脸数据库上的实验结果表明,该方法较其他的传统典型相关分析方法有着更好的识别效果。
关键词:局部保持;典型相关分析(CCA);特征提取;人脸识别
中图分类号:TP391.4 文献标志码:A
doi:10.3969/j.issn.1007-130X.2015.06.021
收稿日期:*2014-02-27;修回日期:2014-06-11
基金项目:国家自然科学基金资助项目 (61373055)
作者简介:
通信地址:214122 江苏省无锡市江南大学数字媒体学院
Address:School of Digital Media,Jiangnan University,Wuxi 214122,Jiangsu,P.R.China
Anewsupervisedlocalitypreservingcanonicalcorrelationanalysisalgorithm
PANRong-hua,CHENXiu-hong,CAOXiang
(SchoolofDigitalMedia,JiangnanUniversity,Wuxi214122,China)
Abstract:From the angle of model recognition, based on Canonical Correlation Analysis (CCA) we propose a new supervised locality preserving canonical correlation analysis (SALPCCA) based on the ALPCCA. By leveraging the useful information of class label, we can expediently construct the nearest neighbor graph and build multi-weighted correlation between samples. Through maximizing the weighted correlation between corresponding samples and their near neighbors belonging to the same classes, the SALPCCA effectively utilizes the class label information and preserves the local manifold structure of the data. Besides, we also propose a kernel SALPCCA (KSALPCCA) based on the kernel methods to better extract the nonlinear features of the data. The experimental results on the face databases of ORL, Yale and AR show that the proposed algorithm has better performance compared with the traditional canonical correlation analysis methods.
Keywords:localitypreserving;canonicalcorrelationanalysis(CCA);featureextraction;facerecognition
1引言
在传统的模式分类问题中,通常能获得一组目标的一组数据来进行分类并做出最终的决策,该组数据形成了被称之为单模的原始特征数据,而从一组目标中获得的多组数据则形成了称之为多模的原始特征数据。近年来,典型相关分析CCA(CanonicalCorrelationAnalysis)[1]作为一种多模的特征提取方法,受到了越来越多的重视和关注。SunQuan-sen等人在文献[2]中对此进行了分析与研究,通过单模数据建立多模数据,使得CCA在人脸识别等领域的应用成为可能。CCA通过最大化两组成对样本之间的相关性从而得到两组典型相关特征,成功解决了模式识别领域的相关问题。CCA是一种全局的线性特征提取方法,由于全局的线性特征提取方法无法有效地提取非线性特征,因此采用这种方法进行非线性学习时,必然会导致欠学习的问题。为了解决这一问题,人们将核方法(KernelMethod)[3,4]应用于CCA,提出了KCCA(KernelCCA)[5,6],它是通过隐式的非线性映射将两组数据分别映射到高维空间,从而能够将低维空间中的非线性问题映射成高维空间中的线性问题,再利用核技巧在高维空间中进行CCA计算,因此该方法能够有效地提取人脸的非线性特征,可以更好地解决人脸识别中的非线性问题。然而,CCA和KCCA同样都没有利用训练样本的类别信息,均是无监督学习。为了充分利用样本的类别信息,判别型典型相关分析DCCA(DiscriminantCCA)[7]被提出,它充分考虑了同类样本与不同类样本之间的相关关系,在实现内类差别最小的同时使得类间的差别最大,类别信息的引入使得DCCA算法相比CCA算法有着更好的识别效果。广义典型相关分析GCCA(GeneralizedCCA)[8],则是将最小化类内散布矩阵作为类信息的同时加入了监督信息,在一定程度上提高了算法的分类识别性能。以上方法只考虑了数据的全局性质,并没有考虑样本数据的局部流形信息。子模式典型相关分析SpCCA(Sub-patternCCA)[9]将局部特征与全局特征的相关性作为判据,达到了融合局部和全局信息的双重效果,同时通过子模式的划分,不仅有效地解决了小样本问题,并较好地描述了人脸识别中的非线性问题。局部保持投影LPP(LocalityPreservingProjections)[10]既提取了样本的特征又保持了样本的局部流形结构,因而具有一些常用流形学习方法的共同优点。局部保持典型相关分析LPCCA(LocalityPreservingCCA)[11]是将局部保持投影的思想引入到CCA,以近邻样本之间的相关取代了全局样本之间的相关,有效地通过线性方式解决了非线性问题,但是LPCCA仍属于无监督学习,文献[12]通过引入监督信息对LPCCA做了一定的改进。
为了更好地挖掘样本局部结构的多样性特征,WangFeng-shan等人[13]提出了一种新的局部保持典型相关分析算法(ALPCCA),它将局部邻域信息融合到CCA中,在高维人脸识别中有着更好的分类效果。但是,ALPCCA也属于无监督学习,为了在保持局部流形结构的同时加入有利于分类的鉴别信息,本文提出了一种有监督的局部保持典型相关分析算法SALPCCA(SupervisedALPCCA)。本文算法在构造样本近邻图时将样本的类别信息考虑在内,避免算法将非同类样本中的相关信息错误地引入,影响最后投影特征的提取。由样本间的距离度量确定权重,建立样本间的多重权重关系,能够增强算法对非典型样本的鲁棒性。利用核方法,在核特征空间中提取样本的非线性特征,提出KSALPCCA(KernelSALPCCA)算法,进一步提高算法解决非线性问题的能力。
2典型相关分析及其相关算法
2.1典型相关分析
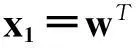
(1)
这里,E表示期望,Sxx和Syy分别表示x和y的协方差矩阵,Sxy表示x和y之间的互协方差矩阵。
2.2判别型典型相关分析
判别型典型相关分析(DCCA)是在传统的典型相关分析的基础上,充分考虑了同类样本和不同类样本之间的相关性及其对分类的影响,它所提取的特征在实现最大化同类样本之间相关性的同时最小化不同类样本之间的相关性,有利于模式分类。
设X与Y为两组特征集,本文均将其表示成矩阵的形式。x∈X⊂Rp和y∈Y⊂Rq分别为其中的两个特征矢量,DCCA的鉴别准则可以表示为:
(2)
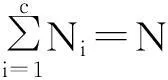
2.3核典型相关分析

(3)
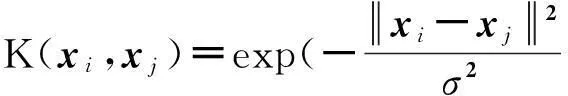
2.4一种最新的局部保持典型相关分析
局部保持典型相关分析(LPCCA)在高维数据上的鉴别能力并不理想,从而在一定程度上限制其在人脸识别中的应用。与LPCCA不同,一种新的局部保持典型相关分析(ALPCCA)直接对最原始的CCA的目标函数改进得到,其鉴别准则表示如下:
(4)
其中:
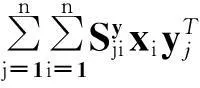
X(I+Sx+Sy)YT
其中,X与Y是两个样本集的矩阵形式,协方差矩阵Cxx和Cyy的定义与CCA中相同;NE(xi)为样本xi∈X的k近邻集,NE(yi)类似;Sx和Sy为相似矩阵,tx与ty为两个可调整的参数,其与LPCCA中的含义相同。I为单位矩阵。
在ALPCCA算法中,当Sx和Sy的所有元素都为零时,ALPCCA就等价于CCA,所以ALPCCA算法是通过额外地加入近邻样本的相关性在CCA中植入了邻域信息;而在LPCCA算法中,当Sx和Sy的所有元素均为1时,即将所有的元素都加入邻域,此时LPCCA等价于CCA,所以LPCCA是通过去除非近邻样本的相关性而在CCA中植入邻域信息,因此LPCCA算法的性能在很大程度上依赖于相似矩阵的计算。然而,在人脸识别问题中,样本的维数往往都很高,相似矩阵Sx和Sy很难估算准确,这在一定程度上影响了LPCCA算法的识别效果。而ALPCCA算法同时使用了局部邻域信息和协方差矩阵,从而能够很好地缓解由相似矩阵计算的不精确所造成的影响,使得该方法比LPCCA有着更好的识别效果。
3有监督的局部保持典型相关分析
3.1有监督的ALPCCA算法
ALPCCA相比LPCCA有着明显的优势,但与一些有监督的算法如DCCA相比,识别效果却明显不足。究其原因是因为ALPCCA在选取近邻时没有考虑样本的类别信息,因而很可能引入不同类别样本中的错误相关信息,从而导致错误的分类,分类环境越是复杂,这种情况越为明显。因此,本文将样本的类别信息引入ALPCCA,试图提出一种有监督的局部保持典型相关分析算法。
DCCA是在CCA的基础上考虑样本的类别信息,使得同类中的所有样本之间建立相关性,是一种有监督算法。但是,DCCA认为同类样本之间的相关性相等,而一般情况下,同类样本之间的相关性会随着样本之间距离的变化而有所不同,样本间的距离越小,相关性越大,反之,相关性则越小,因此DCCA不能很好地描述一些非线性问题。而ALPCCA充分利用了样本的局部邻域信息,考虑了样本之间的距离与相关性的关系,能够较好地描述一些非线性问题,但却没有利用样本的类别信息,是一种无监督算法。因此,结合DCCA和ALPCCA各自的优势,综合考虑样本的局部邻域信息与类别信息,在样本的同类内建立邻域权重相关,提出一种有监督的局部保持典型相关分析(SALPCCA),从根本上消除了ALPCCA算法在不同类样本间建立错误的相关对分类造成的影响,使得从样本中提取的特征更为有效,更有利于最后的分类。同时,SALPCCA以近邻间的权重相关取代了DCCA中同等视之的类内相关,并且以距离作为权重度量的依据,从而能够很好地抑制噪声对算法稳定性的影响,增强了算法的鲁棒性。本文算法具体描述如下。
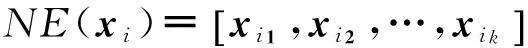
(5)
其中,c(xi)表示xi的类别。
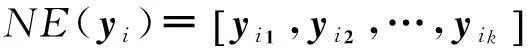
(6)
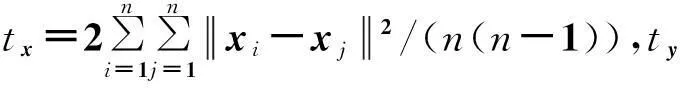
其次,让样本集X中的样本及其近邻样本与样本集Y中相应的样本及其近邻样本建立权重相关。于是,SALPCCA的鉴别准则可以表示为:
(7)
其中,
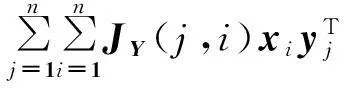
XJYYT=X(I+JX+JY)YT
上述准则亦可表示为以下优化模型:
(8)
利用Lagrangian方法可以将上述优化问题转化为如下的广义特征值分解问题:
(9)
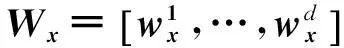
利用特征矩阵Wx和Wy通过以下两种特征提取策略进行特征提取:
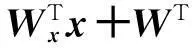
(10)
(11)
由此可以得到两种不同的融合特征。两种特征融合策略用FS1和FS2表示,分别对应于式(10)和式(11)中的两种组合方式。
最后,分类策略采用基于特征矩阵的最近邻分类器进行分类。
综上所述,SALPCCA的算法求解步骤如下:
步骤1输入已标准化的训练样本集X及其对应的样本集Y。
步骤2按照式(5)和式(6)式的方法构造X和Y的类内k近邻矩阵JX和JY。
步骤3根据式(9)式计算投影矩阵Wx和Wy。
步骤4利用式(10)和式(11)式分别进行特征提取,并采用最近邻分类器进行分类。
3.2核化的SALPCCA算法
为了更好地提取样本的非线性特征,利用核方法,将SALPCCA进行推广得到核SALPCCA算法(KSALPCCA)。KSALPCCA不仅利用样本的类内近邻信息将全局非线性问题转化为若干局部线性问题,有效地解决了人脸识别中的全局非线性问题,同时通过利用核技巧能够更有效地提升算法处理非线性问题的能力。因而,本文的算法能有效地刻画人脸识别中的非线性问题,可以提取到鉴别性更强和更能反映样本分布情况的投影轴,具有更好的识别效果。


(12)
采用上节中类似的方法可以求得投影矩阵:

进一步可以得到:
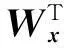
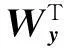
最后做类似于式(10)和式(11)的特征融合,并采用最近邻分类器进行分类。

Figure 1 Sample images from the face database ORL,Yale,AR,respectively 图1 ORL、Yale、AR部分人脸示例图像
4实验与结果分析
4.1人脸库
为验证SALPCCA、KSALPCCA算法的有效性,分别在ORL、Yale、AR三个人脸数据库中进行仿真实验,并与SLPCCA、ALPCCA、LPCCA以及DCCA等算法进行比较。
ORL人脸数据库[14]包括了40个人的人脸图像,每人10幅图像,分别拍摄于不同的时间和光照条件下,具有不同的表情和面部细节。本文实验中随机选取每个人的5幅图像作为训练样本空间X,剩余部分用作测试。利用原图像四级小波分解后的低频分量作为Y。
Yale人脸数据库[15]包含15个人的人脸图像,每人11幅,包括光照方向(左、右和正面)、眼睛、表情变化(正常、愉快、悲伤、困乏、惊讶和眨眼)共165幅灰度图像,图像尺寸为120×91像素。每人选取5幅图像作为训练样本空间X,其余6幅作测试。同样对原图像进行四级小波分解的低频分量作为Y。
AR人脸数据库[16]由126个人(男70人,女56人)的4 000余幅彩色图像构成,每人26幅图像,每幅图像的大小为50×40像素,分为两组,每组13幅,拍摄时间间隔为两周,分别反映了人脸的表情、光照和遮挡的变化。本实验中,选择AR人脸库中的前120个人标号为1~7、14~20的14幅没有遮挡的图像进行人脸识别实验,并随机选取每人的5幅图像作为训练样本空间X,其余作测试。对原图像进行三级小波分解的低频分量作为Y。
4.2实验结果
实验中统一采用Daubechies正交小波对原图像进行分解以获取低频分量,然后利用主成分分析PCA(PrincipalComponentAnalysis)对样本进行降维以解决小样本问题。近邻数目统一设定为训练样本数减1。算法中的核函数选择高斯核函数,X与Y特征集中的核参数σx与σy为标量,其数值在103左右通过交叉验证来确定。传统的PCA与LDA算法通过直接串联后提取特征进行实验。在每个人脸库中分别随机地进行10次独立实验,实验结果见表1~表3。
从表1~表3的实验结果可以看出,本文算法在三个人脸库中的识别率都要高于其他相关算法。

Table 1 Average recognition accuracy of different algorithms on ORL face database

Table 2 Average recognition accuracy of different algorithms on Yale face database

Table 3 Average recognition accuracy of different algorithms on AR face database
有监督算法SLPCCA、SALPCCA的识别率均要高于其相对应的无监督算法LPCCA、ALPCCA,可见类别信息的引入消除了不同类样本间建立错误的相关对分类问题造成的影响,提高了算法的识别效果。在DCCA、SLPCCA和SALPCCA三种有监督算法中,SALPCCA算法的识别率在三个人脸数据库中均高于其他两种算法,这也体现了本文算法同时考虑类内邻域信息和协方差矩阵的优势。KSALPCCA算法的识别率普遍都要高于SALPCCA,可见核化之后的算法更有效地提取了样本的非线性信息,对识别率有一定的提高。由表2可见,由于Yale人脸库中图像数据较少,KSALPCCA也很难提取到更多有利于鉴别的信息,因此KSALPCCA与SALPCCA的识别率相差不大。另外,在ORL人脸库中,由于该数据库中同类别的人脸变化相对不大,因此LPCCA也取得了相对不错的识别率;而在Yale和AR人脸库上,人脸的变化相对较为复杂,LPCCA很难获得较理想的识别率。对比两种特征融合策略可以发现,一般情况下,FS2特征融合策略的识别效果都优于FS1。
图2给出了三个人脸库中各个算法的平均识别率随特征维数变化的趋势,由于PCA和LDA与其他算法结果差距较大,因此为了增强图表的可读性它们不在图表中显示。同时为了统一比较,以下实验均采用FS2的特征融合方式。

Figure 2 Variation of the average recognition rates along with dimensionality on ORL,Yale,AR face databases 图2 六种算法在三个人脸数据库上的 平均识别率随维数变化的示意图
从图2a可以看出,随着特征维数的增加,各个算法的识别率都有所上升,当特征维数增加到一定程度时,识别率会保持在一个相对稳定的水平。观察图2b可以发现,由于DCCA算法受样本类别总数的限制,其最大特征维数只能取到15,这在一定程度上限制了算法的性能,因此其识别效果不如SLPCCA和SALPCCA算法。在图2b和图2c中,识别率先随着特征维数的增加而上升,当识别率达到峰值时,一些算法的识别率会随着特征维数的增加反而有所下降,尤其是LPCCA下降的最为明显,由于其最初提出的目的并不是针对模式分类问题,因此它受维数变化的影响较大且识别效果不理想。但是,本文的算法同时考虑了样本的类内近邻权重相关信息和协方差矩阵,保持了样本的局部流形信息,使得SALPCCA的高维特征中包含了较少的噪声信息,同时核化后的KSALPCCA进一步提升了算法处理非线性问题的能力,因此识别率会随着维数的增加而保持在一个相对较高、较稳定状态。
为了证明本文算法对近邻数k选择的鲁棒性,统一在人脸数据较为丰富的Yale和AR人脸数据库中进行对比实验。实验结果如图3所示。
观察图3的两幅图可以发现,LPCCA算法的识别率随着k的变化波动很大,对近邻数k的选择很敏感。而ALPCCA算法由于其同时考虑了局部邻域信息和协方差矩阵,因此受近邻数的影响并不大,这也体现了ALPCCA算法相对于LPCCA算法的优势。有监督的SLPCCA和SALPCCA算法则表现得更为稳定,可见类别信息的引入,从根本上避免了算法在不同类样本间建立错误的相关,有效地提升了算法的性能,增强了算法的鲁棒性。再仔细观察SALPCCA与ALPCCA算法不难发现,SALPCCA算法在识别率和对k选择的鲁棒性上都要优于ALPCCA算法,这也证明了本文算法的有效性。
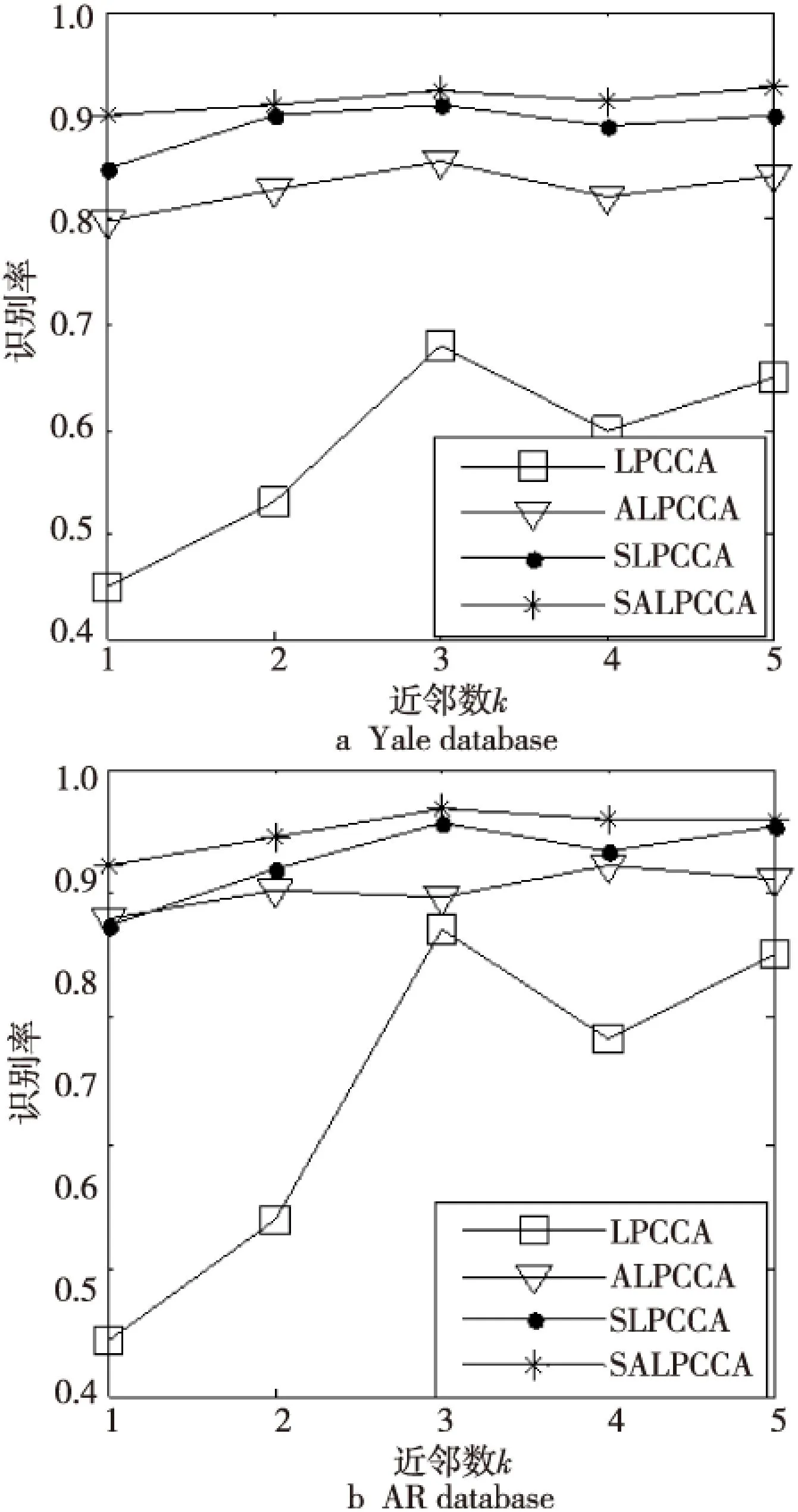
Figure 3 Classification accuracy versus different values of the number of neighbors k in LPCCA, ALPCCA, SLPCCA and SALPCCA on Yale and AR databases 图3 LPCCA,ALPCCA,SLPCCA和SALPCCA 四种算法在Yale和AR两个人脸数据库上的 平均识别率随近邻数k变化的示意图
5结束语
本文以ALPCCA为基础,在考虑样本的类别信息的同时引入近邻样本间权重相关的概念,通过使类内的成对样本与其近邻样本的权重相关性最大,提出了一种有监督的局部保持典型相关分析(SALPCCA)算法,并利用核方法进行核化,提出核化的有监督局部保持典型相关分析(KSALPCCA)。在ORL、Yale、AR人脸库上的实验结果表明,本文的算法相比ALPCCA、SLPCCA、LPCCA以及其他算法有着更好的识别效果和鲁棒性。
参考文献:
[1]HotellingH.Relationsbetweentwosetsofvariates[J].Biometrika, 1936, 28(3):321-377.
[2]SunQuan-sen,ZengSheng-gen,LiuYan,etal.Anewmethodoffeaturefusionanditsapplicationinimagerecognition[J].PatternRecognition, 2005, 38(12):2437-2448.
[3]BoserBE,GuyonIM,VapnikVN.Atrainingalgorithmforoptionalmarginclassifiers[C]//Procofthe5thAnnualACMWorkshoponComputationalLearningTheory, 1992:1.
[4]NelloC,JohnST.Supportvectormachinesandotherkernelbasedmethods[M].Cambrige:CambrigeUniversityPress,2000.
[5]LaiPL,FyfeC.Kernelandnonlinearcanonicalcorrelationanalysis[J].InternationalJournalofNeuralSystems, 2000,10(5):365-377.
[6]MelzerT,ReiterM,BischofH.Appearancemodelsbasedonkernelcanonicalcorrelationanalysis[J].PatternRecogniton,2003,36(9):1961-1971.
[7]SunTing-kai,ChenSong-can,YangJing-yu,etal.Asupervisedcombinedfeatureextractionmethodforrecognition[C]//ProcoftheIEEEInternationalConferenceonDataMining, 2008:1043-1048.
[8]SunQuan-sen,LiuZheng-dong,HengPheng-ann,etal.Atheoremonthegeneralizedcanonicalprojectivevectors[J].PatternRecognition, 2005, 38(3):449-452.
[9]HongQuan,ChenSong-can,NiXue-lei.Sub-patterncanonicalcorrelationanalysiswithapplicationinfacerecognition[J].ActaAutomaticaSinica, 2008, 34(1):21-30.(inChinese)
[10]HeXiao-fei,YanShui-cheng,HuYu-xiao,etal.Facerecognitionusinglaplacianfaces[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2005, 27(3):328-340.
[11]SunTing-kai,ChenSong-can.LocalitypreservingCCAwithapplicationstodatavisualizationandposeestimation[J].ImageandVisionComputing, 2007, 25(5):531-543.
[12]HouShu-dong,SunQuan-sen,XiaDe-shen.Supervisedlocalitypreservingcanonicalcorrelationanalysisalgorithm[J].PatternRecognitionandArtificialIntelligence, 2012, 25(1):144-149. (inChinese)
[13]WangFeng-shan,ZhangDao-qiang.Anewlocality-preservingcanonicalcorrelationanalysisalgorithmformulti-viewdimensionalityreduction[J].NeuralProcessLett, 2013, 37(2):135-146.
[14]SamariaFS,HarterAC.Parameterisationofastochasticmodelforhumanfaceidentification[C]//Procofthe2ndIEEEWorkshoponApplicationsofComputerVision, 1994:138-142.
[15]BelhumeurPN,HepanhaJP,KriegmanD,etal.EigenfacesVsFisherfaces:Recognitionusingclassspecificlinearprojection[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 1997, 19(7):711-720.
[16]MartinezA,BenaventeR.TheARfacedatabase[R].TechnicalReport24,Barcelona,Spain:ComputerVisionCenter(CVC), 1998.
参考文献:附中文
[9]洪泉,陈松灿,倪雪蕾.子模式典型相关分析及其在人脸识别中的应用[J].自动化学报,2008,34(1):21-30.
[12]侯书东,孙权森,夏德深.一种监督的局部保持典型相关分析算法[J].模式识别与人工智能,2012,25(1):144-149.

潘荣华(1989-),男,江苏吴江人,硕士生,研究方向为数字图像处理和模式识别。E-mail:prh__@126.com
PANRong-hua,bornin1989,MScandidate,hisresearchinterestsincludeimageprocessing,andpatternrecognition.

陈秀宏(1964-),男,江苏泰兴人,博士,教授,CCF会员(E200017407M),研究方向为数字图像处理和模式识别。E-mail:xiuhongc@jiangnan.edu.cn
CHENXiu-hong,bornin1964,PhD,professor,CCFmember(E200017407M),hisresearchinterestsincludeimageprocessing,andpatternrecognition.

曹翔(1990-),男,江苏南通人,硕士生,研究方向为数字图像处理和模式识别。E-mail:540034496@qq.com
CAOXiang,bornin1990,MScandidate,hisresearchinterestsincludeimageprocessing,andpatternrecognition.
