基于改进的Mean Shift鲁棒跟踪算法

2016-01-08徐海明,黄山,李云彤

计算机工程与科学 2015年6期

基于改进的MeanShift鲁棒跟踪算法*

徐海明1，黄山1,2，李云彤1

(1.四川大学电气信息学院，四川成都 610065;2.四川大学计算机学院，四川成都 610065)

摘要：Mean Shift跟踪算法在目标尺度变化大和被遮挡时存在较大的缺陷。针对这一问题，提出了一种基于多级正方形匹配的自适应带宽选择和分块抗遮挡的目标跟踪算法。该算法采用目标中心点的离散程度和增量试探法计算出可能的变化尺度，然后采用多级正方形匹配法预测目标的运动趋势，将巴氏系数最大者的尺度作为Mean Shift核函数新的带宽。同时，对前景目标进行分块，根据子块的遮挡程度自适应改变子块权重并按一定准则融合有效子块的跟踪结果。实验结果表明，该算法具有很好的鲁棒性。

关键词：Mean Shift；目标跟踪；多级正方形匹配；分块

中图分类号：TP391.41 文献标志码：A

doi:10.3969/j.issn.1007-130X.2015.06.019

收稿日期：*2014-07-14;修回日期：2014-09-24

作者简介:

通信地址：610065 四川省成都市四川大学望江校区基础教学楼B217

Address:Room B217,Basic Teaching Building,Wangjiang Campus,Sichuan University,Chengdu 610065,Sichuan,P.R.China

ArobusttrackingalgorithmbasedonimprovedMeanShift

XUHai-ming1,HUANG Shan1,2,LIYun-tong1

(1.CollegeofElectricalEngineeringandInformation,SichuanUniversity,Chengdu610065;

2.CollegeofComputerScience,SichuanUniversity,Chengdu610065,China)

Abstract:The Mean Shift algorithm has a defect in handling moving targets with large scale change or being obscured. In order to solve this problem, we propose a bandwidth-adaptive and anti-blocking tracking algorithm based on multi-level square matching and fragment. The proposed algorithm uses the centroid deviation of the target model and the bandwidth trials method to compute the possible scales. The motion trend of the target is predicted through the multi-level square matching method, and the scale of the largest Bhattacharyya distance of the candidate targets is selected as the new bandwidth of the Mean Shift kernel function. At the same time, we divide the target into several fragments, adaptively change their weights according to the degree of being obscured, and then fuse the results of effective fragments under certain rules. Experimental results show that this algorithm has good robustness performance on tracking targets.

Keywords:MeanShift;objecttracking;multi-levelsquarematching;fragment

1引言

基于MeanShift的跟踪算法本质上是一种梯度下降方法，对该算法进行迭代直至收敛到相似性函数的局部极大值。ComaniciuD等人[1]提出的MeanShift算法就是利用目标的颜色直方图和MeanShift向量寻找到最相似的团块区域，以此作为目标在当前帧中的真实位置。

现阶段在MeanShift算法方面主要研究了以下几个问题：(1)原始MeanShift算法在跟踪运动目标的过程中带宽是固定不变的，因此不适合用于跟踪目标有尺度变化的情况；(2)当运动前景目标和背景的颜色比较相似时，MeanShift算法由于过度依赖于运动目标的颜色信息，容易导致跟踪丢失；(3)MeanShift跟踪算法是用巴氏(Bhattacharyya)系数来度量候选模型和目标模型之间的相似程度，它对光照变化很敏感，跟踪会不准确[2]；(4)当目标在复杂环境被遮挡时，原始MeanShift算法获得的运动目标的中心坐标误差会很大。文献[3]提出了一种基于MeanShift和Kalman预测的带宽自适应跟踪算法，该算法以Kalman预测目标在下一帧中的位置作为MeanShift迭代初始位置，同时采用增量试探法自动调节带宽，以适应目标的尺度变化。该算法有效地解决了MeanShift算法对尺度变化的适应问题。文献[4]用K-S相似性度量准则对边缘方向直方图和RGB直方图的特征权值进行融合，提高了前景目标与背景颜色相似情况下的跟踪效果。文献[5]对跟踪目标分块，并在跟踪过程中对子块的权重及相应的模板及时更新，有效地提高了运动目标尺度变化及遮挡情况下的跟踪精度。

针对跟踪过程中目标尺度变化和遮挡情况，本文在分析了这些局限性的基础上，采用MeanShift算法作为主体跟踪算法，提出了一种基于多级正方形匹配的自适应带宽选择和分块抗遮挡的目标跟踪算法。实验结果表明，该算法具有较强的鲁棒性和较高的跟踪准确性。

2MeanShift算法

MeanShift算法是利用无参估计的方法，通过对初始目标模板和候选模板间相似性程度的比对进行一系列的迭代，直至收敛找到最优的匹配，从而达到缩小搜索范围、实现跟踪的目的。

(1)初始目标模型描述。

(1)

(2)

(2)候选模型的描述。

如果在当前帧中得到的运动目标的中心点的坐标为y0，那么在下一帧及以后的图像序列中，可能包含有运动目标的区域称之为候选模型区域，记候选区域的中心点的坐标为yi，该候选区域中的像素用xi来表示(i=1,2,…,nh)：

(3)

其中Ch参照式(2)可归一化为常数：

(4)

(3)相似性度量函数。

巴氏距离最为直观的几何意义就是两个向量之间的夹角的余弦值，文献[2]中明确阐述了采用巴氏(Bhattachayrya)系数作为Mean Shift 跟踪算法中的直方图相似性度量的优越性。

巴氏系数，定义为：

(5)

(4)目标定位。

(6)

其中，权值ωi为：

(7)

(8)

经过一系列迭代运算，最终能找到最优的中心。

3优化MeanShift算法

3.1带宽自适应选择

在目标尺寸逐渐缩小时，增量试探法往往可以得到较好的尺度变换效果。然而，当目标尺寸逐渐增大时，带宽的尺寸却很难扩大，反而经常会越来越小[6]。对运动目标尺度变化做了一定的研究后，本人提出了对目标尺度变化趋势预测的多级正方形法，结合目标中心的离散程度和增量试探法的目标尺度更新策略，实现了对尺度变化的运动目标跟踪。

(1)利用权值来统计中心点位置的离散程度[7]。

(9)

其中,xi为候选模板中心点位置，wi为对应第i个候选模板的中心点对目标中心点的权重，y1为由候选模板中心点位置求得的加权平均值，以此作为目标模板中心。

(10)

其中，dev即统计学中的标准差，度量候选模板中心对目标中心的离散程度。

(11)

其中，devpre为上一帧目标中心的离散程度，计算公式与式(10)一致。

(12)

在式(11)和(12)中，Hpre、Wpre为上一帧目标模板的高和宽，H、W为预估计当前帧图像中标示运动目标区域的高和宽。通过统计跟踪框内候选目标的中心位置的离散程度来相应地改变下一帧中搜索候选目标的中心位置的范围，如果统计出来的当前离散程度与上一帧离散程度大，就按比例扩大在下一帧中候选目标中心位置的搜索范围的大小；如果统计出来的当前离散程度比上一帧离散程度小，就按比例缩小在下一帧中候选目标中心位置的搜索范围的大小；如果统计出来的当前离散程度比上一帧离散程度相等，就保持在下一帧中候选目标中心位置的搜索范围的大小。

(2)四级同心正方形组的建立。

如图1所示，四层正方形的边长比例设定为l3∶l2∶l1∶l0=4∶3∶2∶1。最外层正方形的边长为初始模板中标示运动目标区域的矩形框的宽W和高H之间的最小值。即：

l3=Min(H，W)

(13)

同样在候选模板区域上的质心点也即MeanShift算法收敛点处也建立四级正方形。通过上述四级同心正方形组在初始目标模板上分割出四个区域，分别为Region_A0、Region_A1、Region_A2、Region_A3；同样以MeanShift算法收敛点(即候选模板)为中心，建立四级同心正方形组，分割出四个区域，分别为Region_B0、Region_B1、Region_B2、Region_B3。如图1和图2所示。

Figure 1　Length and zoning of the fourth-level square 图1　四级正方形区域划分与边长

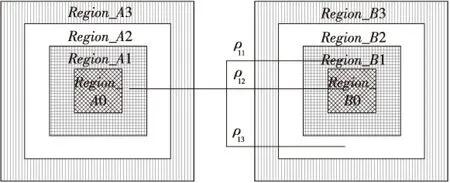
Figure 2　Square matching between candidate target and initial model 图2　候选模板和初始模板间的正方形组匹配图

视频序列中运动目标面向摄像机运动，其尺寸变大，初始目标模板中的区域Region_A1对应的像素点应该大部分对应地扩散到候选目标区域Region_B2；如果运动目标尺寸变小，初始目标模板中的区域Region_A1对应的像素点应该大部分对应地收缩到候选目标区域的Region_B0。如图2，用代表区域Region_Ai和区域 Region_Bj建立模型间的巴氏距离。目标尺度的变化和Region_A1与Region_Bi{i=0,1,2}之间的变化关系：

可以得出如下结论：当运动目标的尺度几乎没有变化时，ρ10、ρ11、ρ12三者之中ρ11最大，同时ρ21、ρ22、ρ23三者之中ρ22最大。因为目标尺度没有变化，那么区域Region_A1和区域Region_B1之间的直方图模型匹配度最高，对于Region_A2和区域Region_B2之间也是如此；同理，运动目标的尺度缩小时，相应区域Region_A1中表征运动目标的特征收缩到区域Region_B0中，因此，ρ10和ρ21取到最大值；同理，运动目标尺度增大时, ρ12和ρ23应该取到最大值。因此通过回字形区域的直方图相似度间的关系可以用来确定运动目标的尺度变化的趋势。

(3)找算法收敛点。

在当前帧中采用MeanShift算法找到收敛点，即当前帧中的候选目标的中心点，以该中心点为中心，分别以上一帧目标模板的宽Wpre和高Hpre，采用增量试探法中建立矩形的方式分别建立三个矩形：高分别为H1、Hpre、H2，宽分别为W1、Wpre、W2。其中H1= Hpre×(1-ɑ)，H2= Hpre×(1+ɑ)，W1= Wpre×(1-ɑ)，W2= Wpre×(1+ɑ)。再建立以式(11)和式(12)中预测的当前帧中目标模板的宽w和高h，采用增量试探法中建立矩形的方式分别建立三个矩形：高分别为h1、h、h2，宽分别为w1、w、w2。其中h1=h×(1-ɑ)；h2=h×(1+ɑ)；w1=w×(1-ɑ)；w2=w×(1+ɑ)。本文中ɑ 取值为10%。

(4)距离决策机制。

在选取初始模板的同时要记录其中心点的位置坐标(xorigin,yorigin)。在当前帧中采用MeanShift算法找到收敛点，即当前帧中的候选目标的中心点(x1,y1)。在该点处，分别计算ρ10、ρ11、ρ12、ρ21、ρ22、ρ23。若ρ12>ρ10,ρ12>ρ11且ρ23>ρ21，ρ23>ρ22，表明运动目标的尺度变大，对Hpre、H2、h、h2这四个尺度进行对比，巴氏距离最大者就是尺度最优者，作为当前帧中运动目标的尺度也就是新的核函数的带宽。若ρ11>ρ10,ρ11>ρ12,且ρ22>ρ21，ρ22>ρ23，表明当前的目标尺度无较大变化，因此对Hpre、H1、H2、h、h1、h2这六个尺度对比，巴氏距离最大者就是尺度最优者，作为当前帧中运动目标的尺度也就是新的核函数的带宽。若ρ10>ρ11，ρ10>ρ12,且ρ21>ρ22，ρ21>ρ23，表明运动目标的尺度变小，对Hpre、H1、h、h1这四个尺度对比，巴氏距离最大者就是尺度最优者，作为当前帧中运动目标的尺度也就是新的核函数的带宽。

采用目标中心点的离散程度和增量试探法计算出几个目标的可能变化尺度，然后采用多级正方形匹配的方法对目标的运动趋势进行预测，把巴氏系数最大者的尺度作为核函数新的带宽，得到较好的尺度变换效果。

3.2分块抗遮挡

传统的MeanShift算法模型过分依赖于颜色直方图，丢失了目标各个部分的空间位置信息，导致跟踪目标被遮挡时效果不佳。本文对目标进行分块，实际上就是更好地使用跟踪目标的空间信息，使MeanShift算法具有更好的鲁棒性。常用分块选择为图3a和图3b结合的方式，这种分块方式需要对每帧做两次不同方向的分块，计算量较大。

本文在跟踪过程中将目标分割成多个互不遮挡的矩形子块，如图3c所示。对每一个矩形子块都将目标颜色信息作为跟踪依据，减弱跟踪窗口中和遮挡程度高的子块的权重，并按一定准则融合有效子块的跟踪结果，最后求得整个跟踪目标在该帧中的中心坐标，达到跟踪效果最佳的目的。对于整体遮挡面积在70%左右的情况，图3c的分块方式仍可以保证两个子块能够具有比较好的跟踪效果。

Figure 3　Methods of fragment 图3　分块方法

基于分块的MeanShift跟踪算法框架下的每个子块都是一个独立的目标。对每个子块跟踪结束后，计算每个候选子目标与原来子目标之间的相似性程度。设ρj为第j个子分块的巴氏系数，选出候选子目标与原子目标最相似的子块，即巴氏系数最大的子块的运动信息作为整个目标的运动信息。然后用整个目标的新位置来更新其他子块的位置，再对下一帧进行处理。但是，当目标受到遮挡时，仅仅依赖于一个子块的跟踪位置来确定整个目标的位置是有一定风险的[8]，有时会产生跟踪漂移的情况，所以要综合考虑多个子块的跟踪情况。当ρj<ρ_th时认为子块j所在区域有遮挡情况出现，本文取ρ_th=0.7。记下没有被遮挡子块的数目Nnon，如果Nnon≥1，则候选目标的位置由相似性程度最高子块j′的位置与其他未被遮挡子块的位置加权来决定：

(14)

其中，yj是每个子块在MeanShift迭代收敛后的位置，devij是每个子块的中心相对整体目标中心的偏移，w表示权重，本文取0.8。当Nnon=0时，表示所有候选目标中的子块与原子块之间的相似性程度都较小，候选目标位置就由所有子块按各自相似性程度加权来决定：

(15)

3.3实验结果

(1)实验环境。

为了验证本文算法的效果，我们对四川大学基础教学楼B座的同一段监控视频进行了不同的实验，分别使用原始MeanShift算法、基于增量试探的MeanShift算法以及本文提出的改进算法对运动目标进行跟踪实验，并对其做了跟踪效果分析。

该实验在英特尔酷睿2双核T5550 1.83GHz笔记本处理器，2GB内存配置下的PC上，使用OPENCV2.4.9与VS2010的开发平台，采用C/C++语言进行编程实现，视频图像的大小为320×240。

(2)尺度变化跟踪实验结果及算法比对。

视频中的目标与摄像机的距离远近使得其对应图像的尺寸呈远小近大的现象[9]。实验图中F代表当前帧数，由于三种算法手动开始框的第一帧都一样，所以只用图4a一幅图表示初始帧结果图。图4b是原始MeanShift算法的跟踪结果，由于原始算法带宽固定不变，所以跟踪时不能自适应改变跟踪框的大小。图4c为文献[3]的算法，能对跟踪框自适应改变大小，但是跟踪效果欠佳。图4d为本文算法，对尺度变化的目标跟踪的结果较好。

Figure 4　Results of scale change 图4　尺度变化结果

对比基于增量试探法的MeanShift算法和本文的改进算法的跟踪误差大小，采用文献[10]定义的指标进行量化比较。其量化公式为：

(16)

FPRi越小，就说明第i帧图像中跟踪结果越准确。

Table 1　FPR i from different algorithms

从表1中计算所得FPRi结果可以看出，当目标尺度发生变化时，文献[3]跟踪算法效果比传统MeanShift算法要好，本文提出的算法比文献[3]算法的效果更佳。

(3)抗遮挡跟踪实验结果及算法比对。

图5是使用文献[3]算法跟踪目标的结果图，当有遮挡时(如第726帧小部分遮挡，第732帧中大部分遮挡)，目标中心的定位存在很大的误差。图6是本文提出的算法，能很好地反映目标变化的尺寸，同时对目标中心定位准确，而且抗遮挡效果较好。

Figure 5　Results of reference [3] 图5　文献[3]算法结果

Figure 6　Results of the proposed algorithm 图6　本文算法结果

算法第707帧第726帧第732帧第995帧文献[3]算法1.36672.26672.38384.3433本文改进算法1.34331.57671.58733.4476

(4)复杂背景环境实验结果及算法分析。

该实验是银行门口的监控视频，图7是使用文献[3]算法在复杂环境下跟踪目标的结果图，当有遮挡且背景颜色相近时，目标中心的定位存在很大的误差，且遮挡情况严重时(F=3 336)直接跟丢目标了。图8是本文算法，鲁棒性效果较好。

Figure 7　Results of reference [3] in chaotic environment 图7　复杂背景下文献[3]算法结果

从表2和表3中计算所得FPRi结果可以看出，基于文献[3]跟踪算法对有遮挡情况和离摄像头较近尺度变化较大时的跟踪效果不佳。本文提出的算法在对目标尺度变化大并有遮挡情况时的跟踪的误差要比文献[3]算法小得多，符合预期期望。

Figure 8　Results of the proposed algoritym in chaos environment 图8　复杂背景下本文算法结果

算法第3279帧第3305帧第3314帧第3336帧文献[3]算法1.45261.77541.72351.9231本文改进算法1.45264.87965.28338.0121

从表4耗时数据可以看出，本文提出的算法虽然在对目标尺度变化大并有遮挡情况时的跟踪的精度能符合预期期望，但是计算量以及本文算法所耗费的时间远大于文献[3]算法，这是本文改进算法的一个不足之处。

Table 4　 Time cost of different

4结束语

针对MeanShift算法本身无法对核函数带宽进行自适应的更新的缺陷，提出了目标中心的离散程度与多级正方形匹配结合的核函数带宽的更新策略。利用目标中心点的离散程度和增量试探法计算出几个目标的可能变化尺度；然后采用多级正方形匹配计算各回字形区域之间的巴氏距离来预测目标的尺度变化趋势；然后对该趋势下的几个目标尺度进行巴氏距离比对，巴氏距离最大者为当前核函数的带宽，即目标的尺度。而且跟踪过程中还对前景目标实行分块跟踪，更好地使用跟踪目标的空间信息，这样能有效地抵抗不同面积遮挡，进一步增强了算法的鲁棒性。实验使用基于增量试探法的MeanShift算法和本文提出的改进算法对运动目标进行跟踪实验，并对其做了跟踪效果分析，证明了该算法的有效性。但是，该算法耗时较大。接下来，我们将研究降低算法的时间复杂度，从而进一步提升跟踪算法的高效率，为将来的运动行为分析打好基础。

参考文献:

[1]ComaniciuD,MeerP.Meanshift:Arobustapproachtowardfeaturespaceanalysis[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,2002,24(5):603-619.

[2]ComaniciuD,RameshV,MeerP.Real-timetrackingofnon-rigidobjectsusingMeanShift[C]//ProcofIEEEConferenceonComputerVisionandPatternRecognition,2000:142-149.

[3]WangWen-jiang,HuangShan,ZhangHong-bin.Bandwidth-adaptivetrackingalgorithmbasedonMeanShiftandKalmanprediction[J].ComputerEngineering&Science,2013,35(5):87-92.(inChinese)

[4]ZhouFang-yan,TangJian,HeJin-song.Adaptivemulti-featurecombinationobjecttrackingbasedonblocking[J].ComputerEngineering,2013,39(4):239-242.(inChinese)

[5]DongWen-hui,ChangFa-liang,LiTian-ping.Adaptivefragments-basedtargettrackingmethodfusingcolorhistogramandSIFTfeatures[J].JournalofElectronics&InformationTechnology,2013,35(4):770-776.(inChinese)

[6]PengNing-song,YangJie,LiuZhi,etal.AutomaticselectionofkernelbandwidthforMeanShiftobjecttracking[J].JournalofSoftware, 2005,16(9):1542-1550.(inChinese)

[7]JeyakarJ,BabuRV,RamakrishnanKR.Robustobjecttrackingwithbackground-weightedlocalkernels[J].ComputerVisionandImageUnderstanding,2008,112(3):296-309.

[8]GuXing-fang.Robustobjecttrackingusingfragments-basedMeanShiftandforeground/backgroundinformation[J].JournalofHangzhouDianziUniversity,2011,31(6):75-78.(inChinese)

[9]LiY,ZhaoW.Adaptiveupdatingofkernelband-widthforMean-Shifttracking[J].JournalofComputationalInformationSystems,2012,8(22):9569-9579.

[10]LiPei-hua,XiaoLi-juan.MeanShiftbasedobjecttracking

withsimilarityandaffinetransformations[J].JournalofImageandGraphics,2011,16(2):258-266.(inChinese)

[11]LiPei-hua.AnimprovedMeanShiftalgorithmforobjecttracking[J].ACTAAutomaticaSINICA,2007,33(4):347-354.(inChinese)

参考文献：附中文

[3]王文江,黄山,张洪斌. 一种基于MeanShift和Kalman预测的带宽自适应跟踪算法[J]. 计算机工程与科学,2013,35(5):87-92.

[4]周芳燕,唐建,何劲松. 基于分块的自适应多特征融合目标跟踪[J]. 计算机工程,2013,39(4):239-242.

[5]董文会,常发亮,李天平. 融合颜色直方图及SIFT特征的自适应分块目标跟踪方法[J]. 电子与信息学报,2013,35(4):770-776.

[6]彭宁嵩,杨杰,刘志,等.MeanShift跟踪算法中核函数窗宽的自动选取[J]. 软件学报,2005,16(9):1542-1550.

[8]顾幸方. 基于分块与前景/背景信息的MeanShift目标跟踪[J]. 杭州电子科技大学学报,2011,31(6):75-78.

[10]李培华,肖莉娟. 基于MeanShift的相似性变换和仿射变换目标跟踪算法[J]. 中国图形图像学报,2011,16(2):258-266.

[11]李培华. 一种改进的MeanShift跟踪算法[J]. 自动化学报,2007,33(4):347-354.