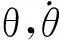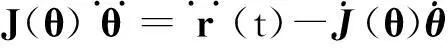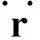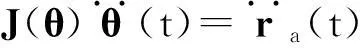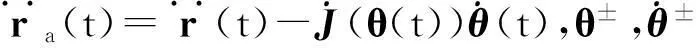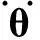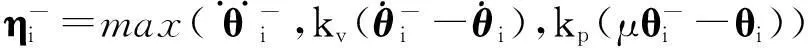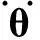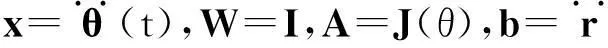多连杆机械臂加速度层最小运动规划和控制策略

多连杆机械臂加速度层最小运动规划和控制策略*

肖林1，严慧玲2，周文辉1，廖柏林1

(1.吉首大学信息科学与工程学院，湖南 吉首 416000;2.吉首大学数学与统计学院，湖南 吉首 416000 )

摘要：为实现多连杆机械臂在加速度层最小运动规划和控制，提出了一个基于最小加速度范数的运动控制策略.该方案通过二次规划的描述，考虑机械臂的关节角、关节速度和关节加速度极限约束，在运动控制过程中规避了机械臂的物理极限.为高效地控制机械臂运动，提出计算复杂度较低的迭代控制算法.六连杆机械臂仿真实验结果验证了最小加速度方案及其迭代控制算法的有效性.

关键词：多连杆机械臂；加速度层；运动控制方案；控制算法;二次规划

文章编号：1007-2985(2015)06-0044-05

中图分类号：TP24文献标志码：A

DOI:10.3969/j.cnki.jdxb.2015.06.011

收稿日期：*2015-06-11

基金项目：国家自然科学基金资助项目(61503152)；吉首大学校级课题(15JDX020)；吉首大学实验室开放基金资助项目(JDLF2015013)；湖南省教育厅优秀青年项目(15B192)，吉首大学实验教学改革研究资助项目(2015SYJG034)；吉首大学2015年大学生研究性学习和创新性实验计划资助项目

作者简介：肖林(1986—)，男，湖南邵阳人，吉首大学信息科学与工程学院讲师，博士，主要从事人工智能、机器人和神经网络等研究.

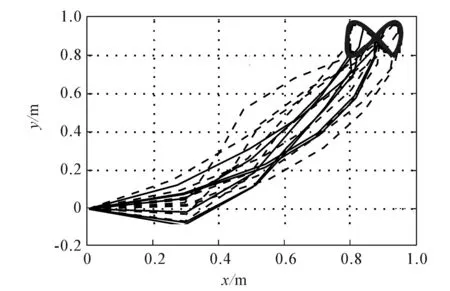
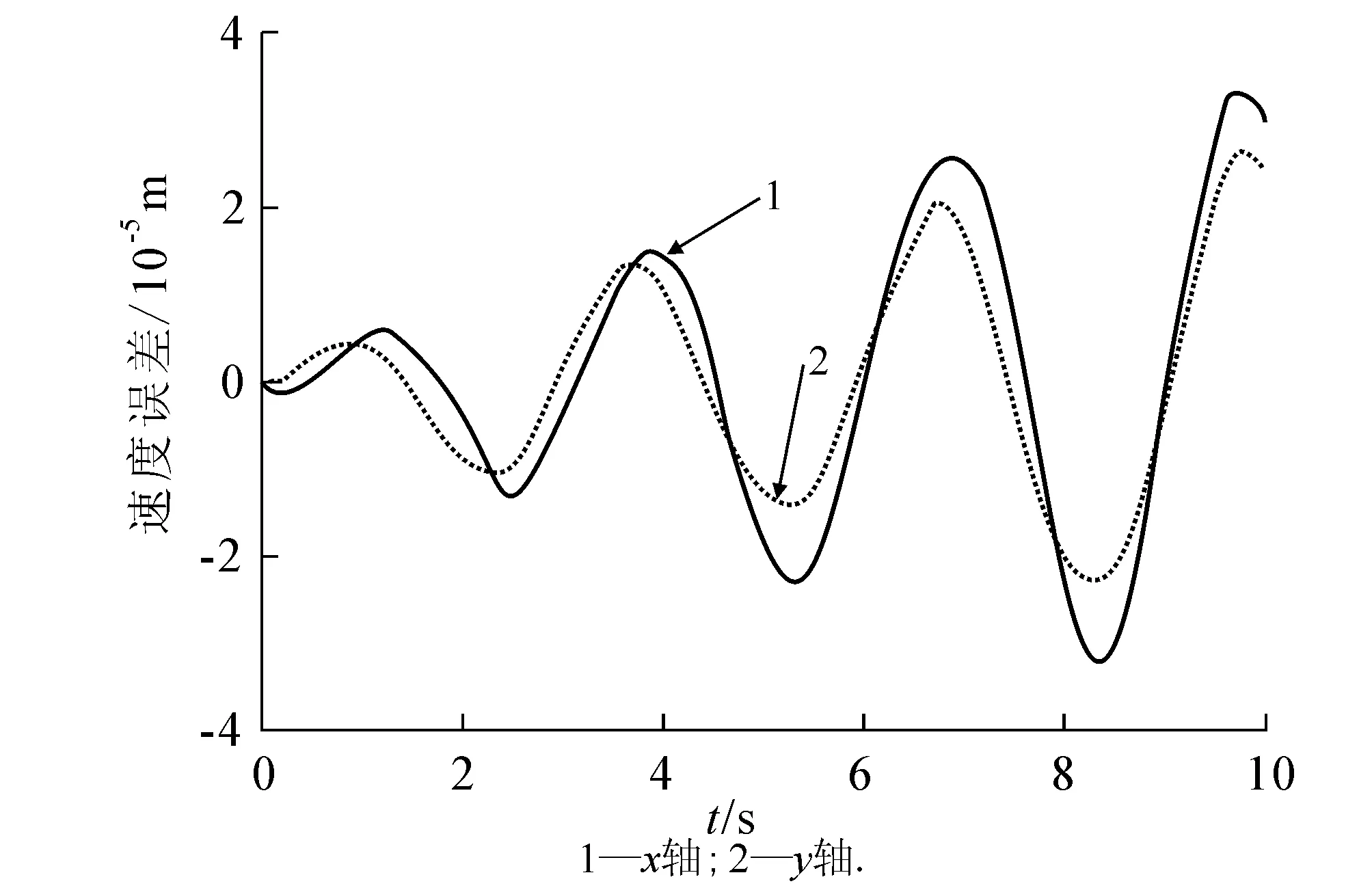
社会的进步与科技的发展，促使人类迫切期望能从重复、繁重和危险的劳动工作中解放出来.机器人技术的出现使得这一切逐渐变为现实.在冗余机器人运动学的研究中，正运动学给定关节变量，由已知的函数映射关系能唯一确定末端执行器的位置；逆运动学给定机械臂的末端执行器的位置变量r(t)∈Rm，则可求解机械臂的关节变量θ(t)∈Rn.对对冗余机械臂来说，m

作为机器人技术中的一个方向，冗余度机械臂的运动规划与控制研究在国内外都有相应的研究与发展[2-3].传统的做法是采用基于伪逆的方案，将问题的解变换为一个最小范数解加上一个同类解.该方案的优点是形式简单，缺点是在处理不等式约束上有困难，而且它会遇到算法奇异情况而生成不可行解.目前大多数的研究都是集中在速度层面上，这对于一些在加速度层面上控制的机械臂而言，就不再有效了.

考虑到伪逆方法无法在不等式基础上解析冗余度问题，笔者提出基于二次规划的冗余度解析方案.该冗余度方案是在加速度层进行解析的，它不仅可以包含角速度关节约束和速度关节约束，而且可以包含加速度关节约束，从而能有效地解决机械臂在加速度层上运动规划和控制的问题.

1加速度层运动规划和控制方法

1.1 前向运动学理论

f(θ)=r(t)，

(1)

其中f(·)：Rn→Rm为一个连续的、非线性的多对一映射.对于一个给定的冗余机械臂，函数f(·)的结构和参数是已知的.因此，对(1)式求微分就可以得到在速度层上求解冗余度解析问题的一阶微分方程：

(2)

1.2 最小加速度方案

考虑机械臂的物理约束，在加速度层提出基于二次规划的冗余度解析方案.该方案对于冗余机械臂而言，既可以实现机械臂的最小加速度运动控制，也能够保证机械臂的关节变量保持在它的极限范围内.

最小化问题(Ⅰ)：

其受约束条件为

(3)

θ-≤θ(t)≤θ+，

(4)

(5)

(6)

1.3 方案等效转换策略

(7)

η±的第i对元素分别定义为

经过以上等效变换，最小加速度运动控制方案问题(Ⅰ)，(3)—(6)式就可以转换成为一个标准的二次规划：

最小化问题(Ⅱ)：

其受约束条件为

Ax=b，

(8)

η-≤x≤η+，

(9)

2迭代控制算法的开发

对于标准的二次规划问题，可以调用Matlab里面的“quadprog”函数直接求解，但因其包容面太广，求解效率不是特别高.笔者开发一个更加有效的离散时间迭代控制算法来求解标准二次规划问题(Ⅱ)和(8)，(9)式.

在对偶决策变量的辅助下，根据对偶理论，对偶二次规划问题可以从标准的原二次规划问题(Ⅱ)和(8)，(9)式推导而来.为了减少离散时间迭代控制算法的计算复杂程度，仅需要定义(8)式的对偶决策变量.由文献[4-5]可以得到如下2个结论：

(1)若二次规划问题存在最优解，则求解二次规划问题(Ⅱ)和(8)，(9)式等效于求解如下的线性变分不等式：

(u-u*)T(Mu*+p)≥0.

(10)

原对偶决策变量u∈Rn+m和它的双端u±∈Rn+m定义为

其中：y∈Rm为(8)式的对偶变量，1v=(1,…,1)T代表的是由“1”组成的向量，常数ϖ=1010∈R可用来在数值上取代+∞.增广矩阵M和增广向量p定义为

(2)若二次规划问题存在最优解，则求解线性变分不等式(10)等效于求解如下的分段线性投影方程：

PΩ(u-(Mu+p))-u=0.

(11)

其中PΩ(·):Rn+m→Ω是空间RN到集合Ω的一个分段投影算子，其第i个元素定义为

至此，求解二次规划问题(Ⅱ)和(8)，(9)式就可以等效于求解分段线性投影方程(11).为了求解分段线性投影方程(11)，受文献[4-5]中算法的启发，定义一个向量取值的误差函数

e(u)=u-PΩ(u-(Mu+p)).

(12)

显然，求解分段线性投影方程(11)就等效于求方程(12)的一个零点.

(13)

由(13)式迭代控制算法产生的序列{uk}，对所有的u*∈Ω*，须满足

且序列{uk}能全局收敛到解u*上，它的前n个元素构成了二次规划问题(Ⅱ)和(8)，(9)式的最优解x*∈Rn.通过分析迭代控制算法(13)的计算复杂度，不难发现，在1次迭代内，它仅需要2N2+3N+1个乘法和2N2+5N-2加法操作，可以大大降低计算复杂度.

3仿真试验

其中：fx(θ(0))，fy(θ(0))分别为初始位置向量f(θ(0))的x轴和y轴的元素分量；ψ表示该方程的设计参数，且ψ=8cm.六连杆机械臂跟踪∞类型的路径跟踪任务仿真试验结果如图1—5所示.

图1　平面六连杆机械臂的运动跟踪轨迹

平面六连杆机械臂的整个运动跟踪过程如图1所示.从图1可知，平面六连杆机械臂完成了一个∞类型的路径跟踪任务.平面六连杆机械臂实际的跟踪轨迹和期望路径的对比如图2所示.通过对比可以发现，跟踪轨迹和期望路径是完全重合的.跟踪轨迹和期望路径对应的位置误差和速度误差如图3，4所示.从图3，4可知，位置误差和速度误差的x轴和y轴取值都小于4×10-5m，这个误差值说明文中所提出来的控制算法十分有效.平面六连杆机械臂的末端执行器在整个过程中的角速度ω变化如图5所示.从图5可知，在最后时刻，末端执行器的最终速度为0.如果最终速度不为0，那么机械臂的末端执行器在任务执行的最后时刻不会立即停下来.

图2　实际跟踪轨迹和期望路径的对比

图3　实际跟踪轨迹和期望路径的位置误差对比

图4　实际跟踪轨迹和期望路径的速度误差对比

图5　平面六连杆机械臂的末端执行器速度变化曲线

4结论

最小加速度范数的运动控制方案考虑到各种关节的物理极限，采用离散时间迭代控制算法求解了标准二次规划问题.平面六连杆串联机械臂的试验仿真结果表明，最小加速度运动方案在控制规划中行之有效，且实际的跟踪轨迹和期望的路径的位置误差控制在一个非常低的数量级内(4×10-5m).

参考文献：

[1]李海丰，王怀超.基于建筑特征及二维地图的复杂城市场景中移动机器人视觉定位算法.计算机应用,2014,34(9):2 557-2 561.

[2]张万绪，张向兰，李莹.基于改进粒子群算法的智能机器人路径规划.计算机应用,2014,34(2):510-513.

[3]简毅，张月.移动机器人全局覆盖路径规划算法研究进展与展望.计算机应用,2014,34(10):2 844-2 849.

[4]HE B.Solving a Class of Linear Projection Equations.Numerische Mathematik,1994,68(1):71-80.

[5]HE B,LIAO L Z.Improvements of Some Projection Methods for Monotone Nonlinear Variational Inequalities.Journal of Optimization Theory and Applications,2002,112(1):111-128.

[6]XIAO Lin,ZHANG Y.Acceleration-Level Repetitive Motion Planning and Its Experimental Verification on a Six-Link Planar Robot Manipulator.IEEE Transactions on Control Systems Technology,2013,21(3):906-914.

MinimumMotionPlanningandControlofAcceleration-Velocity

LevelforMulti-LinkRobotArms

XIAOLin1,YAN Huiling2,ZHOU Wenhui1,LIAO Bolin1

(1.CollegeofInformationScienceandEngineering,JishouUniversity,Jishou416000,HunanChina;2.Collegeof

MathematicsandStatistics,JishouUniversity,Jishou416000,HunanChina)

Abstract:To realize the minimum motion planning and control of multi-link robot arms at the acceleration-velocity level,a norm-based minimum acceleration movement control scheme is proposed and investigated.Different from other schemes,the proposed scheme involves the joint-angle,joint-velocity,and joint-acceleration constraints via using quadratic program formulation.Thus,the redundant robot arms can avoid the physical constraints during motion control process.In addition,in order to control the movement of robot arms effectively,an iterative control algorithm with less computation complexity is developed.Finally,a planar six-link manipulator is employed as an experimental platform to track an ∞-type path task.Simulative results verify the effectiveness of the minimum acceleration scheme and the corresponding iterative control algorithm.

Keywords:multi-linkmanipulators;acceleration-velocitylevel;motioncontrolscheme;controlalgorithm;quadraticprogram

(责任编辑陈炳权)