周期调制倾斜光晶格中单粒子混沌输运特性

周期调制倾斜光晶格中单粒子混沌输运特性*

朱博，林娟萍，钟宏华

(吉首大学物理与机电工程学院，湖南 吉首 416000)

摘要：研究周期调制倾斜光晶格中单粒子的混沌动力学行为，在强调制强度情形下探讨了混沌对粒子量子输运的影响.仿真分析结果表明，只有当调制频率与晶格倾斜度相匹配时，才会发生混沌帮助量子隧穿现象，否则混沌帮助局域化.外场调制方法能有效地操控粒子的量子输运.

关键词：混沌；庞加莱截面；周期调制；量子输运

文章编号：1007-2985(2015)06-0035-05

中图分类号：O562文献标志码：A

DOI:10.3969/j.cnki.jdxb.2015.06.009

收稿日期：*2015-10-25

基金项目：国家自然科学基金资助项目(11465008);湖南省自然科学基金资助项目(2015JJ2114);湖南省教育厅重点资助项目(14A118)

作者简介：朱博(1990—),男,湖南慈利人,吉首大学物理与机电工程学院硕士研究生,主要从事量子物理及其应用研究 通信作者：钟宏华(1983—),男,湖南长沙人,吉首大学物理与机电工程学院副教授,博士，主要从事冷原子物理研究.

经典混沌系统中的量子隧穿和量子输运已成为目前研究的热点.周期调制的双阱体系和光晶格体系是研究上述热点问题的混沌系统[1-5].通过调节调制频率和光晶格的倾斜度，可以有效操控体系的局域化和非局域化.局域化是光晶格体系所特有的典型现象，包括动力学局域化、安德森局域化、遂穿相干破坏.众所周知，安德森局域化与无序有关，而周期调制光晶格中混沌可以代替安德森局域化的无序去引起量子输运的动力学局域化.最近研究发现，量子隧穿的隧穿率的提高与调节经典混沌区域的周期调制有直接联系.随后大量的理论和实验证实了经典混沌的确可以提高量子遂穿率[3-4,7].以前的结果显示，混沌要么帮助局域化，要么帮助非局域化，并形成2种截然相反的结论[10].TANJ等[11]在弱调制光晶格体系下，利用微扰理论探索了能否通过调节参数使混沌帮助局域化的同时，帮助非局域化的问题.笔者进一步研究强调制光晶格体系下混沌对局域化和非局域化的影响，提出了利用外场调制去操控粒子量子输运的方法.

1理论模型

考虑一个单粒子囚禁在周期调制的倾斜光晶格中，相应的哈密顿量为[11]

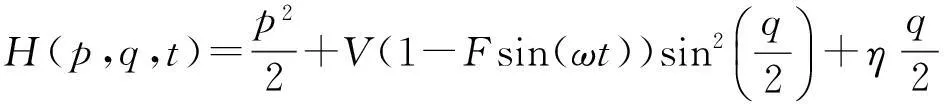
(1)

2体系的混沌与规则区域

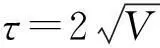
(2)

对于(2)式，当驱动强度F和η/V的值较小时，ε(q,τ)可以看作是一项微扰.其微扰解q(τ)可以写成零阶异宿解q0(τ)和一阶混沌解q1(τ)之和[3-4]，即q(τ)=q0(τ)+q1(τ).基于微扰解可以通过梅尔尼科夫函数去判定体系的混沌和规则区域[9,11,14]，但是对于调制强度F的值相对较大时，ε(q,τ)不能当作微扰项，梅尔尼科夫判据不再适用，需通过数值计算坐标q和动量p的经典庞加莱截面去判定体系是否处于混沌区域还是规则区域[1-2].体系坐标算符q和动量算符p的经典庞加莱截面为

体系关于坐标q和动量p的庞加莱截面如图1所示.

图1　体系关于坐标q和动量p的经典庞加莱截面

为了展示体系的混沌和规则参数区域，选取参数V=5,πη=2，图1a,1b,1c的调制频率ω=2，图1d,1e,1f频率的调制频率ω=5，图1a,1d的调制强度F=0.63,图1b,1e的调制强度F=1.5,图1c,1f的调制强度F=2.

从图1a,1b,1c可知，对于共振参数[11-13]ω=πη=2，随着调制强度F的增加，体系更容易进入高混沌区域.图1a为文献[11]中的微扰情形，本研究仿真结果和微扰处理给出的分析结果一致.图1d,1e,1f的调制给出了ω=5的非共振情形，通过比较发现，对于相同的调制强度F，非共振参数情形体系更容易处于规则区域.因此，为了研究混沌对粒子量子输运的影响，本研究主要考虑共振区域和共振区域附近的参数情形.

3混沌对粒子的量子输运影响

利用最近邻紧束缚近似方法，描述系统量子动力学的哈密顿量(1)式可改写为[5,12]

(3)

其中：|n表示局域在格点n处的Wannier态；J(t)表示相邻格点i,j之间的耦合系数[15]，其表达式为

Wannier态矢|j可写为

|j.

(4)

将体系的量子态写为|ψ(t)an(t)|n，并利用文献中解析求解几率幅an(t)的方法,可解析地给出粒子在格点n处的几率为

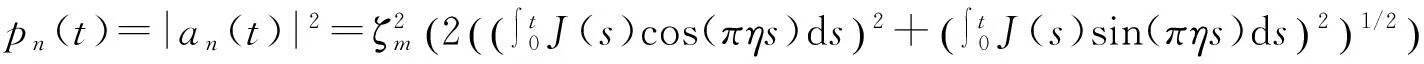
(5)

其中ζm表示第1类m阶贝塞尔函数，相应的初始条件为p0(0)=1,pn≠0(0)=0.为了满足最近邻紧束缚条件，选取光晶格深度V=5，结合(4)，(5)式可求得相邻格点i,j之间耦合系数为

J(t)=-0.028 6-0.016 5Fsin(ωt).

不同频率下粒子在格点n处几率pn(t)随时间演化见图2(F=2,πη=2).对于不同的调制频率ω，粒子在光晶格中分别出现局域化、周期振荡、非局域化现象.对于共振参数ω=πη=2，体系处于高混沌区域(图1c)，混沌可帮助粒子量子隧穿(图2a).当偏离共振频率的偏移量Δω=0.02，即调制频率ω=2.02时，粒子在相邻晶格中周期地振荡，只是振荡周期比较长(图2b)，振荡周期随Δω的增加而减小(图2c).当Δω增加到一定值以后，粒子将完全局域在初始晶格，不发生量子遂穿(图2d).

图2　粒子在光晶格中的动力学演化

定义粒子囚禁在格点n处的几率对时间的平均值为

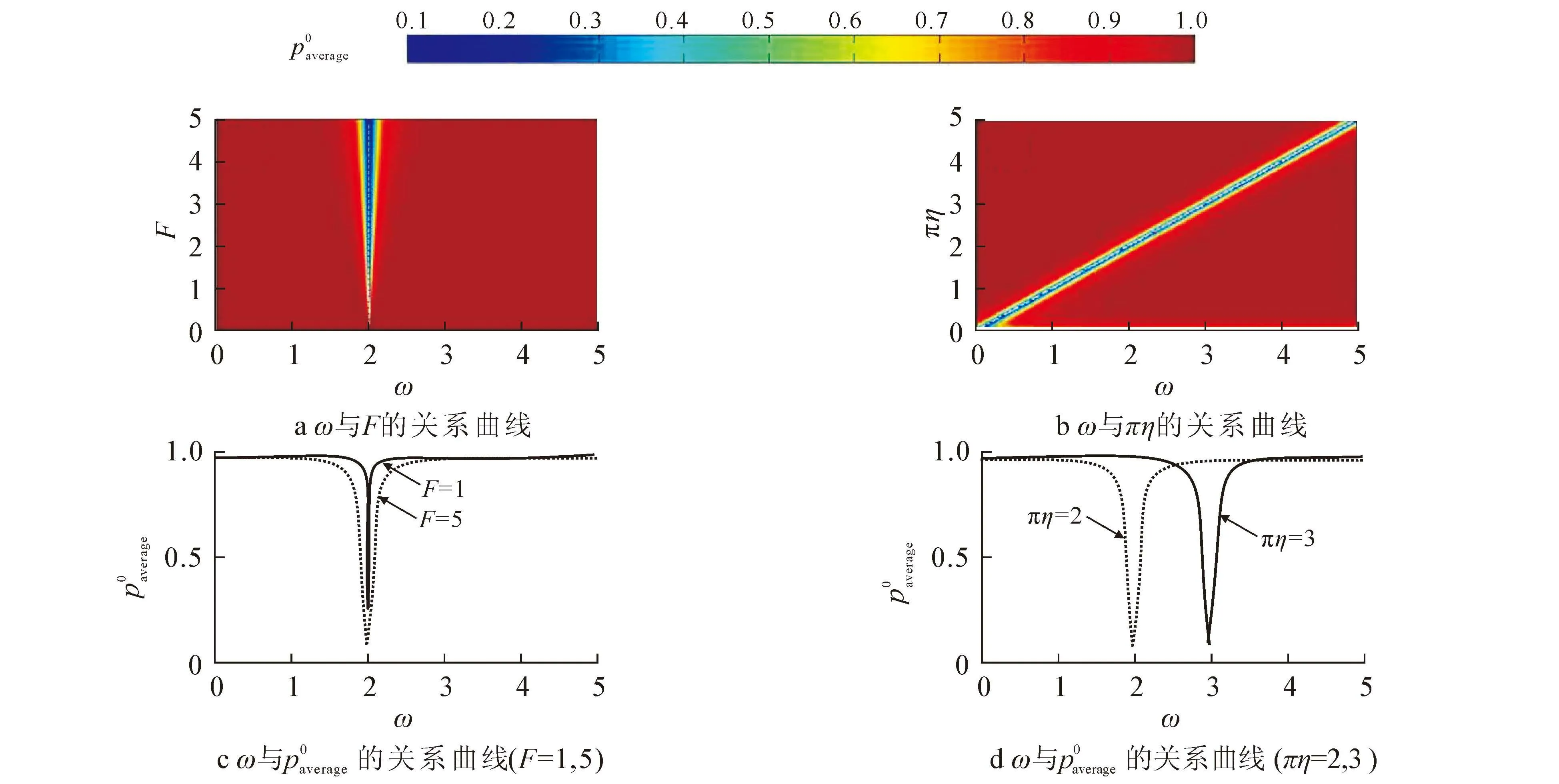
图3　参数F，ω，πη对粒子占据初态平均几率p 0 average的影响

4结语

对于周期调制倾斜光晶格中的单粒子体系，利用庞加莱截面数值给出了体系的混沌区域和规则区域.对于共振参数情形，随着调制强度的增加，体系更容易进入高混沌区域；对于相同的调制强度，非共振参数情形时体系更容易处于规则区域.仿真结果表明，对于不同的调制频率ω，粒子在光晶格中可以出现局域化、周期振荡、非局域化现象.只有当调制频率与晶格倾斜度相匹配时，才会发生混沌帮助量子隧穿现象，否则混沌帮助局域化.因此，通过调节外场调制可以有效地操控粒子的量子输运.

参考文献：

[1]STECKDA,OSKAYWH,RAIZENMG.ObservationofChaos-AssistedTunnelingBetweenIslandsofStability.Science,2001,293(5 528):274-278.

[2]HENSINGERWK,TRUSCOTTAG,UPCROFTB,etal.AtomsinanAmplitude-ModulatedStandingWave-DynamicsandPathwaystoQuantumChaos.JournalofOpticsB:QuantumSemiclassicalOptics,2000,2(5):659-667.

[3]BARTUCCELLIM,CHRISTIANSENPL,PEDERSENNF,etal.PredictionofChaosinaJosephsonJunctionbytheMelnikov-FunctionTechnique.PhysicalReviewB,1986,33(7)：4 686-4 691.

[4]CHONGG，HAIW，XIEQ.SpatialChaosofTrappedBose-EinsteinCondensateinOne-DimensionalWeakOpticalLatticePotential.Chaos,2004,14(2)：217-223.

[5]DUNLAPDH,KENKREVM.DynamicLocalizationofaChargedParticleMovingUndertheInfluenceofanElectricField.PhysicalReviewB,1986,34(6)：3 625-3 633.

[6]ANDERSONPW.AbsenceofDiffusioninCertainRandomLattices.PhysicalReview,1958,109(5)：1 492-1 505.

[7]GROSSMANNF,JUNGP,DITTRICHT,etal.TunnelinginaPeriodicallyDrivenBistableSystem.ZeitschriftFurPhysicalB,1991,84(2)：315-325.

[8]ZHOUZ，HAIW，DENGY,etal.ChaoticTransportofaMatter-WaveSolitoninaBiperiodicallyDrivenOpticalSuperlattice.Chaos,SolitonsFractals,2012,45(11)：1 423-1 429.

[9]MELNIKOVVK.OntheStabilityoftheCenterforTimePeriodicPerturbations.TransactionsoftheMoscowMathematicalSociety,1963,12：1-57.

[10]ARTUSOR，BORGONOVIF，GUARNERII,etal.PhaseDiagramintheKickedHarperModel.PhysicalReviewLetter,1992,69(23)：3 302-3 305.

[11]TANJintao，LUGengbiao，LUOYunrong,etal.DoesChaosAssistLocalizationorDelocalization?[J/OL].Chaos,2014,24(4)：043114.http://dx.doi.org/10.1063/1.4898332.

[12]CHENYuao,NASCIMBNESYLVAIN,AIDELSBURGERMONIKA,etal.ControllingCorrelatedTunnelingandSuperexchangeInteractionswithAC-DrivenOpticalLattices[J/OL].PhysicalReviewLetter,2011,107(21)：210405.http://www.doc88.com/p-59033035900.html.

[13]MARuichao,TAIMERIC，PREISSPHILIPPM,etal.Photon-AssistedTunnelinginaBiasedStronglyCorrelatedBoseGas[J/OL].PhysicalReviewLetter,2011,107(9)：095301.http://www.docin.com/p-373660879.html.

[14]HAIW，LIUX，FANGJ,etal.ControllingCorrelatedTunnelingandSuperexchangeInteractionswithac-DrivenOpticalLattices.PhysicalLetterA,2000,275(1/2)：54-59.

[15]JAKSCHD，BRUDERC,CIRACJI,etal.ColdBosonicAtomsinOpticalLattices.PhysicalReviewLetter,1998,81(15)：3 108-3 111.

ChaoticTransportforSingleParticleinTilted

OpticalLatticewithPeriodicalModulation

ZHUBo,LINGJuanping,ZHONGHonghua

(CollegeofPhysicsandElectromechanicalEngineering,JishouUniversity,Jishou416000,HunanChina)

Abstract:The chaotic dynamic behavior of single particle in the tilted optical lattice with periodical modulation is explored,and the effect of chaos on quantum transport is studied under the strong modulating case.The chaos is found to assist quantum tunneling only when the modulation frequency matches with the gradient of lattice;otherwise,the chaos promotes localization.Therefore,the quantum transport of the particle can be manipulated via adjusting periodical modulation.

Keywords:chaos;Poincarésection;periodicalmodulation;quantumtransport

(责任编辑陈炳权)