确定OWA算子权重的2个新模型

确定OWA算子权重的2个新模型*

谢婉莹，成央金，杨柳，白玉龙

(湘潭大学数学与计算科学学院，湖南 湘潭 411105)

摘要：提出了2个新的模型来确定OWA算子的权重.新的模型根据最小化任意相邻权重间的差距的思想而提出，在给定和值时，通过求解非线性规划问题来确定OWA算子的权重.用一个算例与其他确定权重的模型进行对比，说明2个新模型的可行性.

关键词：OWA算子；权重；和值；模型

文章编号：1007-2985(2015)06-0014-04

中图分类号：F222.1文献标志码：A

DOI:10.3969/j.cnki.jdxb.2015.06.004

收稿日期：*2015-04-27

基金项目：国家自然科学青年

作者简介：谢婉莹(1993—)，女，河南汝南人，湘潭大学数学与计算科学学院硕士，主要从事决策分析研究；央成金(1965—)，男，湖南娄底人，湘潭大学数学与计算科学学院教授，硕士，主要从事运筹学研究.

Ronald R Yager定义的OWA算子为不确定环境下的决策分析问题提供了一个统一的结构体系.不同的决策准则，如最大最大准则(乐观准则)、最小最小准则(悲观准则)、等可能准则及Hurwicz准则，有不同的OWA算子权重.确定权重是在决策分析过程中应用OWA算子的至关重要一环.Michael O’Hagan提出了一个最大熵方法，这个方法是在给定和值时，通过求解一个非线性约束优化问题来确定权重的，其中熵作为非线性规划的目标函数，预先给定的和值作为约束条件，得到的权重和OWA算子分别称为最大熵权重和最大化熵OWA算子.Dimitar Filev等分析了最大熵方法的一些性质.Robert Fullér等认为最大熵模型可以转化为一个多项式进行分析求解.Ronald R Yager[4-6]给出了量词引导集成方法.Filev D等提出了指数平滑法，得到指数OWA算子.David F Nettleton等提出了遗传算法.近来，Robert Fullér等提出了一个最小方差方法获得最小方差OWA算子权重.刘新旺等[10]提出了一个参数几何方法确定最大熵权重.王应明等[11]通过建立一个线性规划模型提出了最小差方法确定OWA算子权重.Gholam R Amin等[12]对最小差方法作了一个扩展延伸.

笔者根据OWA算子的一些基本性质，提出求解OWA算子权重的2个新模型.给定和值后，通过LINGO求解一个非线性规划来确定OWA 算子的权重.

1OWA算子及权重确定方法

OWA算子的权重向量主要由2个函数决定:一个是离差，一个是和值.分别定义如下：

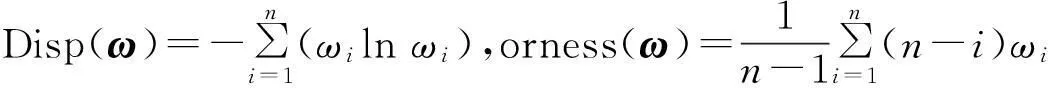
离差代表概率分布函数的熵，和值属于区间[0,1]，代表决策者的乐观度.和值越接近1，则OWA算子越接近“or”算子;和值越接近0，则OWA算子越接近“and”算子;权重越均匀散开，则OWA算子越接近0.5.

文献中提出最大熵的方法，通过求解如下非线性约束优化模型来确定OWA算子的权重：

文献[13]中提出最大Renyi熵模型，通过求解如下非线性优化模型来确定OWA算子的权重：

文献中提出如下最小方差法：

王应明等[11]在给定和值的条件下，提出最小最大偏差方法：

可以化简为一个线性规划模型来求解.Amin G R将上述模型扩展为如下形式：

(1)

下文将分析这些模型的共性，并提出2个新的模型确定OWA算子的权重.

2确定OWA算子权重的新模型

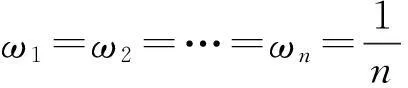
(ⅰ)α=0时，ω=(0，0，…，0，1)T，F(a1，a2，…，an)=max[a]i]；

α=1时，ω=(1，0，…，0，0)T，F(a1，a2，…，an)=min[a]i]；

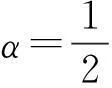
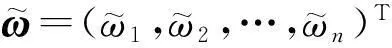
(ⅲ)若i

基于这些特点，提出如下2个新模型确定OWA算子的权重：

(2)

(3)

可以看出这2个模型均是非线性的，能根据LINGO求解.2个模型并不适于α=0及α=1的情形，但可以用α=0.000 1与α=0.999 9近似得到.

3算例

这里通过一个算例与模型(1)对比，说明2个新模型的可行性.假设n=6，计算对应不同和值α=0，0.1，0.2，0.3，…，0.8，0.9，1的OWA算子的权重.

表1　模型(1)确定的OWA算子的权重

表2　模型(2)确定的OWA算子的权重

表3　模型(3)确定的OWA算子的权重

比较表1—3各自的最优OWA算子权重发现，模型(2)，(3)与模型(1)得到的权重是非常接近的，并且满足之前提到的确定OWA 算子权重的模型的共性，说明了这2个模型的可行性.

4结语

参考文献：

[1]MICHAEL O’HAGAN.Aggregating Template or Rule Antecedents in Real-Time Expert Systems with Fuzzy Set Logic//Proceedings of the 22nd Annual IEEE Asilomar Conference on Signals，Systems and Computers.San Jose,CA:Maple Press,1989.

[2]DIMITAR FILEV，RONALD R YAGER.Analytic Properties of Maximum Entropy OWA Operators.Information Sciences，1995，85(1/2/3):11-27.

[3]ROBERT FULLÉR，PETER MAJLENDER.An Analytic Approach for Obtaining Maximal Entropy OWA Operator Weights.Fuzzy Sets and Systems，2001，124(1):53-57.

[4]RONALD R YAGER.On Ordered Weighted Averaging Aggregation Operators in Multicriteria Decisionmaking.IEEE Transactions on Systems Man and Cybernetics，1988，18(1):183-190.

[5]DONALD R YAGER.Families of OWA Operators.Fuzzy Sets and Systems，1993，59(2):125-148.

[6]DONALD R YAGER.Quantifier Guided Aggregation Using OWA Operators.International Journal of Intelligent Systems，1998，11(1):49-73.

[7]FILEV D，DONALD R YAGER.On the Issue of Obtaining OWA Operator Weights.Fuzzy Sets and Systems，1998，94(2):157-169.

[8]DAVID F NETTLETON，VICENÇ TORRA.A comparison of Active Set Method and Genetic Algorithm Approaches for Learning Weighting Vectors in Some Aggregation Operators.International Journal of Intelligent Systems，2001，16(9):1 069-1 083.

ROBERTFULLÉR，MAJLENDERPÉTER.OnObtainingMinimalVariabilityOWAOperatorWeights.FuzzySetsandSystems，2003，136(2):203-215.

[10]LIUXinwang，CHENLianghua.OnthePropertiesofParametricGeometricOWAOperator.InternationalJournalofApproximateReasoning，2004，35(2):163-178.

[11]WANGYingming，CELIKPARKAN.AMinimaxDisparityApproachforObtainingOWAOperatorWeights.InformationSciences，2005，175(1/2):20-29.

[12]GHOLAMRAMIN，ALIEMROUZNEJAD.AnExtendedMinimaxDisparitytoDeterminetheOWAOperatorWeights.ComputersandIndustrialEngineering，2006，50(3):312-316.

[13]PÉTERMAJLENDER.OWAOperatorswithMaximalRényiEntropy.FuzzySetsandSystems，2005，155(3):340-360.

[14]WANGYingming，LUOYing，LIUXinwang.TwoNewModelsforDeterminingOWAOperatorWeights.ComputersandIndustrialEngineering，2007，52(2):203-209.

TwoNewModelsforWeightDeterminationofOWAOperator

XIEWanying，CHENGYangjin，YANGLiu，BaiYulong

(DepartmentofMathematicsandComputationalScience，XiangtanUniversity，Xiangtan411105，HunanChina)

Abstract:This paper proposes two new models for OWA weight determinination based on the minimized disparity of two adjacent weights.The nonlinear optimization problem is solved to obtain the OWA operator weights under a given orness level.Finally，the paper presents a numerical illustration to compare the two models with other models and demonstrate their feasibility.

Keywords:OWAoperator;operatorweights;orness;model

(责任编辑向阳洁)