基于Bootstrap原理的立靶密集度估计

基于Bootstrap原理的立靶密集度估计

彭峰生，舒林森，宁玮

(陕西理工学院 机械工程学院， 陕西 汉中 723000)

[摘要]阐明了Bootstrap抽样的理论和方法，着重对该方法的置信区间等参数估计作了详细研究，应用该方法进行了火炮射击立靶密集度估计实例分析，结果表明该方法对小样本参数估计问题有较高的实用价值。

[关键词]统计与概率；Bootstrap理论；Monte Carlo抽样；参数估计；立靶密集度

[文章编号]1673-2944(2015)05-0066-04

[中图分类号]O212.2

收稿日期：2015-03-19

基金项目：陕西省教育厅科学研究计划项目(15JK1142)

作者简介：彭峰生(1972—)，男，陕西省汉中市人，陕西理工学院高级工程师，博士，主要研究方向为复杂机电系统分析。

长期以来，小子样参数估计和统计分析问题困扰着许多工程实践工作，一些重大项目的试验样机数量很少，一般只有有限的几个，甚至只有唯一的一件样机。这种情况下，通过现场试验测试的数据十分宝贵而有限。如何在少量测试数据的条件下，找出数据的统计特性和规律，为样机的改进提供指导依据，给工程试验数据分析人员带来挑战。

Bootstrap方法[1-2]由美国统计学家Efron首次系统地提出，该方法并不需要对总体分布作假设或事先推导估计量的解析式，它要做的仅仅是重构样本并不断计算估计值，本质上是一种非参数方法[3]。在分布类型未知的情况下，Bootstrap方法为我们提供了解决此类问题的另一种有效思路。

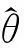
本文通过研究Bootstrap方法和有关统计参数估计的理论，采用样本数据重复抽样的方法增大研究对象的数据样本容量，在此基础上提出参数估计的方法和步骤，并给出参数估计的误差分析与估计办法。最后通过一个工程实例的小样本条件下数据参数估计计算，初步验证了所提出的方法。

1Bootstrap方法参数估计原理

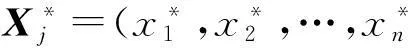
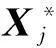
样本参数θ是分布函数F的函数，记作θ=θ(F)。当我们将样本看作总体来处理时，样本分布函数的估计参数应该是总体参数的一个良好估计。参数估计的步骤如下[6]：

(2)重复(1)中的过程B次，B是一个足够大的整数，由此获得了B个容量为n的Bootstrap样本；

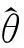
2Bootstrap抽样的置信区间

大多数统计推断涉及到分布参数的估计。最常见的是近似置信区间估计，就是使用样本参数确定特殊区间的一种方法[7]。理想的区间有如下两个特性：(1)该区间包含了参数θ；(2)区间相对来说是较窄的。区间的两个端点称作上、下置信限，它们是随机样本的函数，因而也是随机变量。因此，由一个样本计算出的区间不一定包含θ。当然，如果采用一种合适的区间估计法，不断地重复取样，那么将从每个随机产生的估计区间之中，确定得到以概率C包含参数θ的估计区间。置信度C定义为置信区间包含θ的近似概率。因此，如果C很大(接近于1)，则我们完全可以确信由单个样本计算出的置信区间包含参数θ。

2.1　标准置信区间

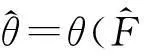
(1)

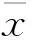
(2)

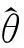
(3)

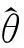
(4)

这里η～N(0，1)，当样本容量n→+∞时，称之为标准正态分布。标准置信区间是根据η～N(0，1)分布推导出来的。

还可得到另一个更好的近似估计，设

(5)

式(5)表明η服从于n-1个自由度的t分布。定义置信度为100(1-α)%的标准置信区间为

(6)

这里α=1-C称为显著性水平。

2.2　百分位置信区间

3应用Bootstrap方法分析火炮射击密集度

火炮用相同的射击诸元对立靶进行多发射击，靶平面上弹着点的分布称为弹着散布。大量统计试验表明：单管火炮的射弹立靶散布服从正态分布[6]。

所有弹着点的平均坐标称为散布中心。以散布中心为坐标原点O，铅直向上为Y坐标，水平向右为Z坐标，建立直角坐标系ZOY。假设射弹散布在Z和Y轴相互独立，则射弹散布服从独立二维正态分布，其分布密度为f(z,y)，即：

(7)

式中z和y分别为弹着点在Z和Y轴上的坐标，σz和σy分别为弹着点在Z和Y轴上散布的均方差。

通过坐标变换可得

(8)

r和θ仍然为独立随机变量，且有

(9)

称r为弹着点的瑞利半径，一定的半径表示一条等概率密度椭圆线。式(8)和(9)就是用瑞利半径表示的弹着散布概率密度的数学表达式[8]。

某型自动炮通过靶场射击试验，取得一组立靶密集度数据(单位：m)：0.732，0.864，0.627，0.563，0.926，0.684，0.981。假设系统误差为0，则由式(2)得标准差σ=0.840 m，弹丸落入瑞利半径R为1.5 m的圆内的概率可由下式求出：

(10)

采用基于Bootstrap方法的蒙特卡洛仿真方法，通过仿真得到一组立靶密集度数据(单位：m)：0.685，0.669，0.673，0.907，0.589，0.801，0.602，0.724，0.826，0.705。将仿真数据与靶场测试试验数据组合，得到一组新的试验数据：0.732，0.864，0.627，0.563，0.926，0.684，0.981，0.685，0.669，0.673，0.907，0.589，0.801，0.602，0.724，0.826，0.705。

同理，假定系统误差为0，则由式(2)得σ=0.770 m，弹丸落入瑞利半径R为1.5 m的圆内的概率可由下式求出：

(11)

显然，通过基于Bootstrap方法的蒙特卡洛仿真方法增加试验数据后，可以明显提高参数评估的置信度水平。

4结束语

Bootstrap抽样分析方法对于解决小样本问题参数估计有独特的优势。其方法简单，可操作性强，只要对初始样本多次重复随机抽样，就可构成容量大的分析样本，从而便于构成统计量。该方法分析精度高，收敛快。

需指出的是，该方法估计参数对初始样本有较强的依赖性。Bootstrap方法是一个复杂的过程，若重复这个过程，每次得到的结果会有轻微的差别。该方法的优点是无需任何样本总体的分布假定，即可获得某一感兴趣的分布参数估计。

[参考文献]

[1]BRADLEY E.Bootstrap methods:another look at the jackknife[J].The Annals of Statistics,1979,7(1):1-26.

[2]BRADLEY E,ROBERT T.An introduction to the Bootstrap[M].New York:Chapman & Hall Ltd,1993.

[3]MOONEY C Z,DUVAL R D.Bootstrapping:A Nonparametric approach to statistical inference[J].Journal of the American Statistical Association,1993(2):427.

[4]BERGES J O.Statistical Decision Theory[M].New York：Springer-Verlay Press，1986.

[5]SHALIZI C.The Bootstrap[J].American Scientist,2010,98(3):186-190.

[6]唐雪梅,张金槐,邵凤昌,等.武器装备小子样试验分析与评估[M].北京:国防工业出版社,2001:7-11,221-224.

[7]金星,洪延姬,沈怀荣,等.可靠性数据计算及应用[M].北京:国防工业出版社，2003.

[8]彭峰生,廖震强,王涛.有脱靶弹时自动火炮立靶密集度估计[J].弹道学报,2008,20(1):66-70.

[责任编辑：张存凤]

Crowding level of vertical target parameters estimation based on Bootstrap sampling

PENG Feng-sheng,SHU Lin-sen,NING Wei

(School of Mechanical Engineering, Shaanxi University of Technology, Hanzhong 723000, China)

Abstract:The paper concentrates on developing the using of Bootstrap sampling methods and relative theories. The crowding level of vertical target of an automatic gun is studied carefully as a real example to explain the usage of the methods. It proves that Bootstrap sampling method is of great value in parameters estimation of small sampling problems.

Key words:statistics and probability;Bootstrap theory;Monte Carlo sampling;parameters estimating;crowding level of the vertical target