房地产风险投资复杂网络与网络间的混沌同步

房地产风险投资复杂网络与网络间的混沌同步

张伟，常娟，毛北行

(郑州航空工业管理学院 数理系， 河南 郑州 450015)

[摘要]将房地产风险投资建模为复杂网络混沌系统，研究了房地产投资风险复杂网络之间的混沌同步问题，基于混沌同步控制理论和Lyapunov函数方法，采用驱动-响应同步策略，给出了误差系统同步的一个充分条件，实现了两个复杂网络之间的混沌同步。

[关键词]复杂网络；房地产；混沌同步

[文章编号]1673-2944(2015)05-0070-03

[中图分类号]O415.5; O157.5

收稿日期：2015-04-03

基金项目：国家自然科学基金数学天元基金资助项目(11226337)；河南省科技厅基础与前沿计划项目(142300410410)；河南省高等学校重点科研项目(15B110011)

作者简介：张伟(1978—)，男，山东省菏泽市人，郑州航空工业管理学院讲师，硕士，主要研究方向为复杂网络与混沌同步。

房地产系统引起了众多学者的关注，文献[1-2]研究了房地产投资风险分析与防范，文献[3]研究了房地产风险投资的评估、评价和管理，但都没有建立房地产复杂网络的数学模型。另一方面，混沌同步是研究的热点问题并取得了很多成果[4-6]，而关于房地产复杂网络混沌同步问题的相关研究还相对不是很多。文献[7]将房地产风险投资系统建模为Lorenz方程组，研究了该类混沌系统的同步问题，但该种模型粗略，与实际吻合性不高。文献[8]建立了一个非线性成本函数下的投资模型，并研究了该模型的稳定性问题，但并没有进一步研究混沌问题。文献[9]将房地产系统建模为细胞神经网络模型，研究了该模型的稳定性分析问题，但并没有进一步研究它的混沌同步问题。文献[10]研究了一类不确定参量复杂网络与网络间的混沌同步问题，但研究的不是房地产问题。本文研究了房地产投资风险时滞复杂网络之间的混沌同步问题，通过设计适当的控制输入，不但实现了两个复杂网络之间的混沌同步，而且网络内部节点之间的耦合强度也被同时确定下来。当房地产投资系统出现混沌现象时，通过调节控制信号，能够及时对房地产金融投资策略做出调整，实现房地产投资系统的协调发展。

1主要结果

考虑如下房地产风险投资系统构成的复杂网络：

(1)

其中xi(t)，xi(t-τ)分别代表t，t-τ时刻市场上房地产开发的数量，i=1，2，…，N；fj(xj(t))，fj(xj(t-τ))分别代表t，t-τ时刻市场上房子的售价；αi1，αi2是网络内部节点之间的耦合强度；aij，bij是表示网络拓扑结构的耦合矩阵A，B的矩阵元。将(1)式描述的房地产复杂网络作为目标网络，受控的响应网络取下列形式：

(2)

其中βi1，βi2是响应网络内部节点之间的待定耦合强度，ui为控制输入。

定义系统的误差为ei(t)=yi(t)-xi(t)，则误差的一阶导数为

条件1 (1)‖fj(yj(t))-fj(xj(t))‖≤η1‖yj(t)-xj(t)‖；

(2)‖fj(yj(t-τ))-fj(xj(t-τ))‖≤η2‖yj(t-τ)-xj(t-τ)‖。

定理1若满足矩阵不等式：

(3)

其中A,B为系统的耦合矩阵。设计

(4)

其中ρi为调控参量，γi1=αi1η1，γi2=αi2η2，响应网络中待定的耦合强度βi1，βi2的自适应律：

(5)

则两个房地产风险投资复杂网络(1)与(2)是混沌同步的。

证明构造Lyapunov函数

求导得

设计适应律

设计控制输入

根据前面条件1，很容易得到：

所以

其中：ξ=[‖e1(t)‖,‖e2(t)‖,‖e3(t)‖,…,‖eN(t)‖]T，η=[‖e1(t-τ)‖,‖e2(t-τ)‖,…,‖eN(t-τ)‖]T。

2数值算例

以市场上两个开发商为例，其中x1(t)，x2(t)为两个开发商在t时刻开发的楼盘数量，τ为时间滞后常数，上述房地产风险投资系统对应的状态方程为：

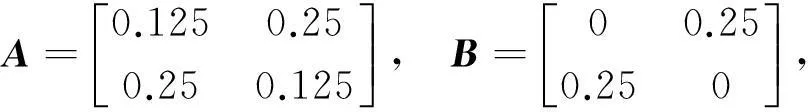
以上述二阶节点为例，其对应的响应系统为：

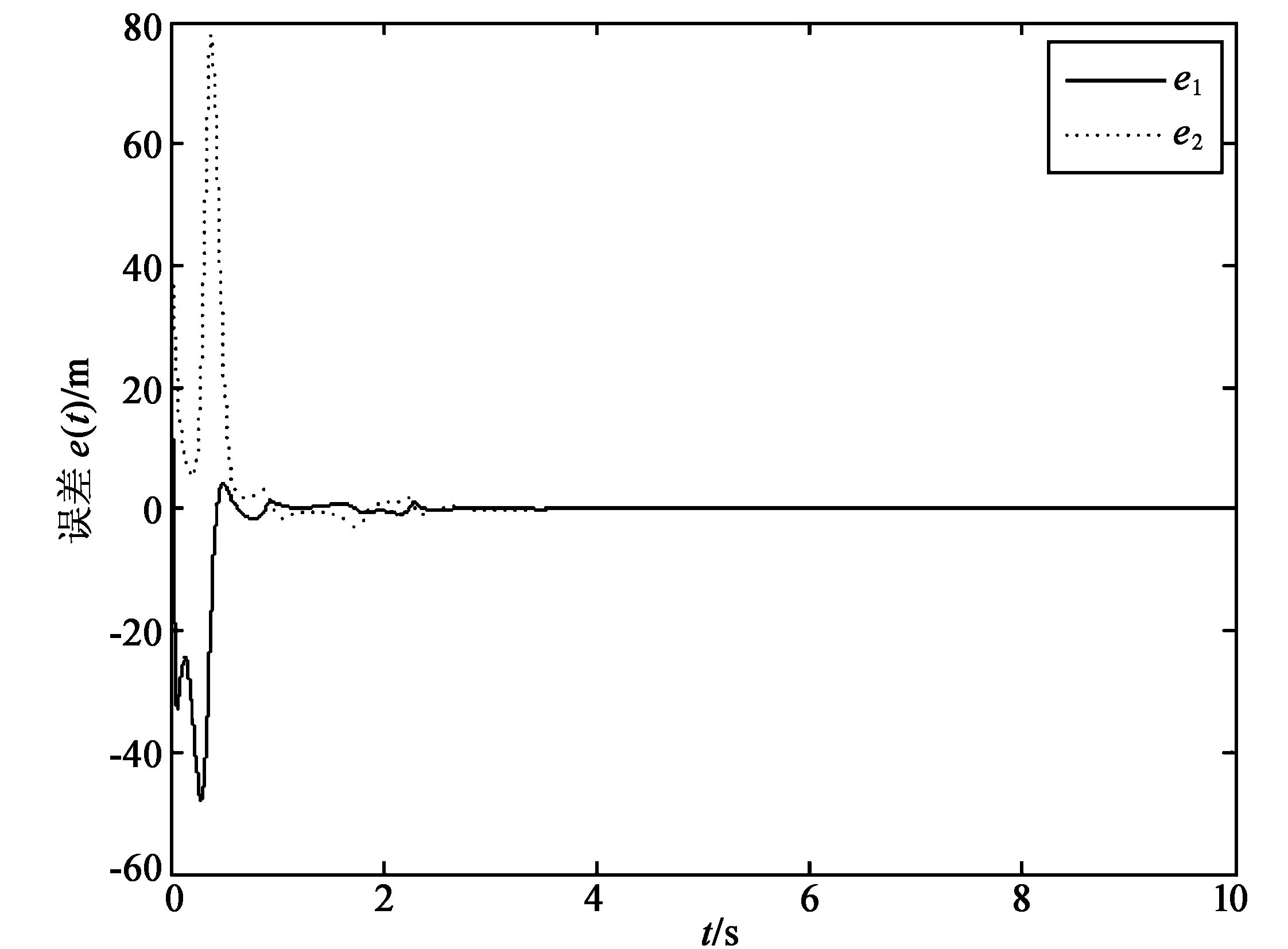
图1　系统的误差响应曲线

系统误差如图1所示。从图中可以看到，在系统达到同步以前，系统误差曲线相差很大，随着时间的推移，当t>0.245 s以后，系统的误差渐趋于零。

3结论

本文实现了房地产投资驱动系统与经济增长响应系统的同步，当房地产投资系统出现混沌现象时，通过调节控制信号，能够及时地对房地产金融投资策略做出调整，实现房地产投资系统的协调发展。

[参考文献]

[1]阮萍,陈志敏.对房地产与投资风险的认识[J].经济问题探索,2000,34(4)：16-19.

[2]张建旭.房地产投资风险分析与防范研究[J].经营与管理,2008,27(1)：23-25.

[3]JANNADI O A,ALMISKARI S.Risk Assessment in Construction[J].Journal of Construction Engineering and Management,2003,132(5)：1331-1335.

[4]卞秋香,姚洪兴.复杂网络的线性广义同步[J].系统工程理论与实践,2011,31(7)：1334-1340.

[5]LORENZ H W,NUSSE H E.Chaotic Attractors,Chaotic Saddles and Fractal Basin Boundaries：Goodwin’s Nonlinear Accelerator Model Reconsidered[J].Chaos Solitons and Fractals,2002,13(5)：957-965.

[6]毛北行,孟金涛.离散复杂网络系统的混沌同步[J].郑州大学学报：理学版,2013,45(3)：9-12.

[7]刘静岩,韩文秀.房地产投资的混沌同步研究[J].天津大学学报：自然科学与工程技术版,2002,35(5)：586-588.

[8]姚洪兴,王国栋.一类房地产投资模型的复杂性分析[J].统计与决策,2008(1)：55-57.

[9]姚洪兴,王娜娜.房地产风险投资模型的稳定性分析[J].统计与决策,2010(11)：41-49.

[10]张檬,吕翎,吕娜,等.结构与参量不确定的网络与网络之间的混沌同步[J].物理学报,2012,61(22)：5081-5085.

[责任编辑：谢 平]

Chaos synchronization between complex networks of the real estate systems

ZHANG Wei,CHANG Juan,MAO Bei-xing

(Department of Mathematics and Physics, Zhengzhou Institute of Aeronautical Industry Management,Zhengzhou 450015, China)

Abstract:This paper gives the complex networks chaos model on real estate investment systems. Chaos synchronization between complex networks of the real estate system is studied in the paper. The sufficient conditions for achieving chaos synchronization of the errors systems are derived using drive-response strategy based on chaos synchronization theory and Lyapunov function approach. The chaos synchronization between two complex networks is realized.

Key words:complex networks； real estate；chaos synchronization