自动连结链聚类算法

自动连结链聚类算法

李隘优

( 闽西职业技术学院 计算机系,福建 龙岩 364021 )

摘要：针对传统聚类算法存在时间性能低效且需要输入参数的缺点，本文提出了一种自动连结链聚类新算法.该算法在确立数据的基础上,通过计算数据点与各顶点的距离并加以排序形成不同群组，然后快速搜寻出它们的相邻点形成连结链网络，再根据连结链的平均距离删除过长的连结链，从而达到聚类的目的.实验结果表明,本文算法与DBSCAN及Single-Link算法具有相同的聚类效果，但执行时间约仅为这两种算法的10%.

关键词：自动连结链； 聚类算法； 象限； 网络

收稿日期：2015-06-28

作者简介：李隘优(1980—)，男，讲师，研究方向为算法分析与设计.

文章编号：1004-4353(2015)03-0254-03

中图分类号：TP309.3

Automatic link-chain clustering algorithm

LI Aiyou

(DepartmentofComputer,MinxiVocational&TechnicalCollege,Longyan364021,China)

Abstract：Time performance for shortcomings and inefficiencies of traditional clustering algorithms require input parameters,this paper proposes a new algorithm. The algorithm on the basis of the data side established by the distance calculation of data points and the vertices and be able to sort the formation of different groups,and then quickly find out their adjacent points form a network link chain,according to the average distance is too long and then delete the link chain link chain,which serve the purpose of clustering. Experimental results show that the execution time of the automatic link chain clustering algorithm accounts for about 10% of the common algorithm.

Key words： automatic link-chain; clustering algorithm; quadrant； network

0引言

群集分析技术[1]由于能够明显突出群体间的差异性，因此被广泛应用于图像识别、数据压缩、影像处理、空间分析和生物信息特征分析等领域.但目前大多群集分析技术算法需要事先给出(或输入)一个或多个参数，而确定适当的这些参数本身就不是一件易事，这不仅加大了聚类分析过程的复杂度，有时也影响了聚类结果[2].例如K-Means聚类算法[3]中，必需代入参数k以确立所要聚类的群体数，并需要反复尝试及验算，才能得到较好的聚类结果，计算量非常大.这类代入参数的聚类算法需建立一套参数范围估算的验算公式，才能有效地执行群集分析.鉴于此，本文引入自动连结链聚类算法(automatic link-chain clustering algorithm，ALC Algorithm)，它无需输入参数，也无需反复针对聚类结果加以尝试及验算.实验表明，该算法既保证了聚类的准确率，又提高了聚类的速度.

1自动连结链聚类(ALC)算法

自动连结链聚类算法是近年来兴起的一个简单聚类方式，它有别于基于阶层式聚类法[4]、基于密度聚类法[5]、基于网格聚类法[6]及基于模型式聚类法[7]，但与分割式聚类法[8]接近.ALC算法在分割群体之前，每一个数据点必需找到各个象限中与它最接近的数据点，然后连结各点形成连结链网络.因此，从网络中很容易就能发现数据点间的分布关系，通过删除过长的连结链，就能达到快速分割群体的目的.本文重点讨论如何在这些数据群中，不输入任何参数且只需使用少量的计算就能建立起连结链网络结构.

ALC算法的具体步骤如下：

1)找出数据点边界顶点.寻找出数据点分布的边界，以边界的顶点作为排序基准点.如对于图1所描绘的数据分布，根据数据点分布的情况寻找数据点的边界，并以A、B、C、D点作为数据的边界顶点.

图1　样本分布边界点

2)数据点对边界顶点排序，形成不同群组.如将图1中数据集合中的数据点分别对边界顶点A、B、C、D进行排序，即计算所有的数据点与A、B、C、D点的欧氏距离(Euclideandistance)：

其中k为维度；用计算出的距离加以排序形成不同群组，群组排序结果以SortA、SortB、SortC、SortD表示.

3) 快速搜寻邻点,形成连结链网络.要存储一个连结链网络数据就必须定义一个数据结构，以便记录连结链网络信息.从任一个数据点开始，根据上面所获得的排序群组来搜寻每个象限中最接近(相邻)的点并计算出它们之间的距离，如果该象限中没有找到相邻的点则以NULL表示；重复上述步骤，直到每个数据点都在每个象限中找到它的相邻的点.最终生成的连结链网络结构如图2所示.

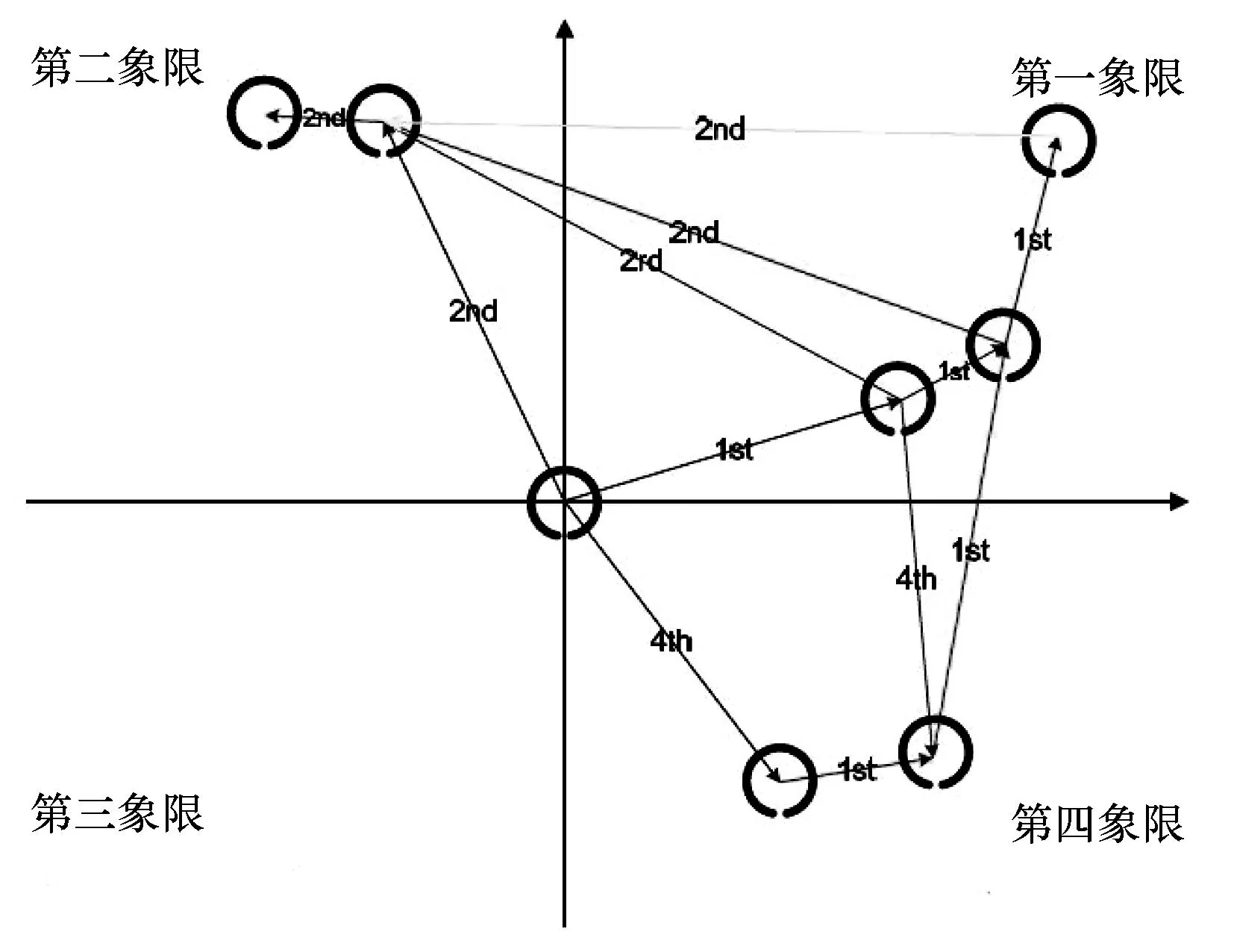
图2　连结链网络生成图

快速搜寻相邻点的方法,如图3所示，以P点搜寻第一象限相邻的点为例，在排序群C序列中找到与P相邻的排序点P2，以P2在排序群C序列中的位置作为搜寻范围的起点；在排序群A序列中找到与P相邻的排序点P1，以P1在排序群C序列中的对应位置作为搜寻范围的终点；在排序群C中，由P2(起点)到P1(终点)间的范围为搜寻范围(图3中虚线所绘区域)，将大幅度地减少寻找相邻点所需要比对数据点的次数，可大大缩短计算机的运算时间.

图3　P点搜寻第一象限的最近点

4)计算连结链的平均距离.生成连结链网络后，必须进行数据分析才可进一步进行聚类.根据所有的连结链的距离(即数据点间的差异性)计算出所有连结链的平均值(DAVG)，并以此作为聚类的标准.

其中Des∈(DesA,DesB,DesC,DesD)，N为有效的连结链总数.

5)删除过长的连结链.根据聚类的评估标准值DAVG进行聚类，删除连结链网络中所有连结链距离大于DAVG的数据，被删除的数据点归到不同的群组中，存在连结链关系的数据点归为同一群组，从而使数据产生群聚，形成聚类效果.

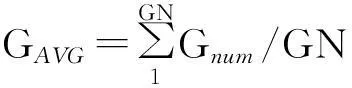
2实验与分析

为分析ALC算法的性能，与传统Single-Link算法、DBSCAN算法进行了对比分析.聚类算法执行时间的实验设计：分别输入500、1000、1500、2000、2500、3000、3500、4000、4500、5000个随机样本点，数据集合为二维坐标点，数据数值范围为±200，分别使用ALC、DBSCAN、Single-Link聚类算法进行群集分析，其中DBSCAN、Single-Link聚类算法分别参考文献[5]与文献[4].由ALC进行群集分析之后，将所得到的DAVG作为DBSCAN算法的Eps及Single-Link算法的Threshold参数值.不同算法执行时间的结果如表1所示.

表1　不同聚类算法执行时间的比较

由表1可知，3种聚类法都能将非固定形状样本数据分出相同的群组数量，但DBSCAN及Single-Link算法都需反复调整Eps及Threshold参数值才能得到较佳的聚类效果.3种聚类算法的效果虽然相同，但执行效率上ALC算法所消耗的时间远小于DBSCAN和Single-Link算法，如图4所示.

图4　不同算法执行时间的比较

3结论

本文提出的自动连结链聚类算法克服了其他聚类算法使用参数而对聚类结果及效率产生不良影响的问题，在不需要输入参数的情况下，通过引入自动连结链的方法，增加了数据点的线性可分概率，即扩大了数据类之间的差异，从而提高了聚类的质量.实验表明，该算法与Single-Link聚类算法及DBSCAN聚类算法具有相同的聚类效果，但其执行时间仅为这两种算法的10%，大大节省了运算时间.由于目前的研究只针对了二维数据样本上的聚类实验，高维度以及其他形态的数据集有待今后进一步地研究.

参考文献：

[1]张晓伟.聚类算法及在搜索引擎系统中的应用[D].哈尔滨：哈尔滨理工大学，2014.

[2]Mali U,Bandyopadhyay S. Genetic algorithm-based clustering technique[J]. Pattern Recognition,2000,33(9):1455-1465.

[3]王辉,张望,范明.基于集群环境的K-Means聚类算法的并行化[J].河南科技大学学报(自然科学版),2008,29(4):42-45.

[4]赵玉艳,郭景峰,郑丽珍,等.一种改进的BIRCH分层聚类算法[J].计算机科学,2008,35(3):180-183.

[5]熊忠阳,吴林敏,张玉芳.针对非均匀数据集的DBSCAN过滤式改进算法[J].计算机应用研究,2009,26(10):3721-3723.

[6]Song B C,Ra J B. A fast search algorithm for vector quantization using L2-norm pyramid of codewords[J]. IEEE Transactions Image Processing,2002,59(11):10-15.

[7]Jim Z C Lai,Yi-Ching Liaw. Fast-searching algorithm for vector quantization using projection and triangular inequality[J]. IEEE Transactions Image Processing,2004,13(12):1554-1562.

[8]吴昌友,王福林,马力.采用链路聚类的动态网络社团发现算法[J].西安交通大学学报,2014，48(8):73-79.