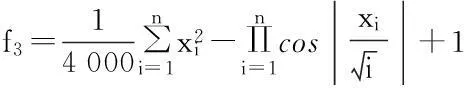基于HKBFO优化神经网络的悬索桥动载识别
2016-01-08陈修辉,孙铭霞
基于HKBFO优化神经网络的悬索桥动载识别
陈修辉1,孙铭霞2
( 1.青岛理工大学 琴岛学院,山东 青岛 266106; 2.长春光华微电子设备工程中心有限公司,吉林 长春 130000 )
摘要:为提高BP神经网络对桥梁动载识别的效果,提出了一种基于分层菌王觅食算法(HKBFO)的桥梁动载识别方法.该算法首先进行“交叉”复制操作,再类比人大代表选举过程进行分层寻优.数值模拟证明,HKBFO算法优于BFO算法,可用于桥梁动载识别.
关键词:分层菌王觅食算法; 神经网络; 悬索桥; 动载识别
收稿日期:2015-07-21
作者简介:陈修辉(1983—),男,讲师,研究方向为运动稳定性与控制.
文章编号:1004-4353(2015)03-0257-04
中图分类号:TU312+.1
Identification of moving load on the suspension bridge based on HKBFO optimized neural network
CHEN Xiuhui1,SUN Mingxia2
( 1.QingdaoCollege,QingdaoTechnologicalUniversity,Qingdao266106,China; 2.ChangchunGuanghua
Micro-ElectronicsEquipmentEngineeringCenterCo.Ltd.,Changchun130000,China)
Abstract:In order to improve the effect of BP neural network on the moving load identification of bridge,a new method of moving load identification method based on the Hierarchical King Bacteria Foraging Optimization algorithm (HKBFO) is proposed. The algorithm first carried on the “cross” copy operation,and then by the analogy of the election process of the People’s Congress conducted hierarchical optimization. The numerical simulation showed that HKBFO is better than BFO,and can be used for bridge moving load identification.
Key words: Hierarchical King Bacteria Foraging Optimization algorithm (HKBFO); neural network; suspension bridge; identification of moving load
桥梁结构在交通中的作用日趋重要,其可靠性对社会和经济的发展有着重大的影响.就目前桥梁结构而言,其结构日趋轻型化,跨度日趋增大化,而在桥梁上运行的车辆载重量和速度也都在不断地提高,极易导致桥梁结构的疲劳损伤甚至破坏,因此桥梁动载识别具有重要的研究意义和应用价值[1-3].根据桥梁的挠度、应变等响应识别桥梁动载已有很多学者对此进行研究,并取得了一些成果,例如:S.S.Law等[4-5]分别利用时域法和频时域法研究了桥梁动载识别;F.T.K.Au等[6]采用二分之一车辆模型对连续梁上移动荷载进行了识别;陈锋等[7]和尤琼等[8]分别利用函数拟合法研究了桥梁动载识别;李忠献等[9]利用BP神经网络识别了桥梁动载;陈震等[10]采用截断广义奇异值分解法研究了桥梁移动荷载识别.近年来,利用BP神经网络进行桥梁动载识别成为常用的方法之一,此方法的关键在于如何训练神经网络,即确定神经网络的拓扑结构和神经网络参数,其中神经网络参数(包括权值和阈值)的确定尤为关键.传统的神经网络参数确定方法中,多存在寻优速度慢、鲁棒性较差、易陷入局部早熟等问题[11-12],对此,本文拟采用分层菌王觅食算法来确定网络参数,并通过数值模拟来验证本文方法的有效性.
1分层菌王觅食算法
细菌觅食算法[13-14](Bacteria Foraging Optimization algorithm,BFO)是由K.M.Passino于2002年提出的一种仿生随机搜索算法,主要包括趋向操作(chemotaxis)、复制操作(reproduction)和迁徙操作(elimination and dispersal),由于其构造简单、易于理解而成为智能算法中的研究热点,并且被广泛应用于诸多优化问题中.但基本BFO算法存在优化精度不高,收敛速度慢,易陷入局部早熟等缺陷,并且在进行复制操作时也只是个体的简单重复,并没有充分利用到最优个体的信息.为此,本文将当前群体中适应度值最优的细菌称为菌王(the king of bacteria,KB),复制操作时每个新细菌都由菌王和当前细菌“交叉”产生,且采用分层结构,底层由一系列子群体构成,顶层由各个底层子群体的子菌王组成,从而提出一种分层菌王觅食算法(Hierarchical King Bacteria Foraging Optimization algorithm,HKBFO).
为充分利用最优细菌个体(菌王)的信息,在进行复制操作时不再是简单的淘汰较差的一半细菌,而是自身复制较优的一半细菌,同时为了提高群体的多样性,在复制操作时按以下方式进行:
设群体的细菌数为N,复制时先将细菌按适应度值由优至劣进行排序,然后直接淘汰较差的N/4细菌,自身复制较好的N/4细菌,然后用较好的N/4细菌替代较差的N/4细菌,中间的N/2细菌按下式进行“交叉”复制:
Pi+N/4(j,k+1,l)=λ·(Pi+N/4(j,k,l)+
(1-λ)·PK(j,k,l)),
Pi+N/4(j,k+1,l)=(1-λ)·Pi+N/4(j,k,l)+
λ·PK(j,k,l),
类比于各级人大代表的选举过程,本文提出了分层的菌王觅食算法.算法的底层由S个彼此独立子群体组成,每个子群体均采用上述的菌王觅食算法进行优化计算;底层各子群体的菌王构成顶层的群体,顶层群体仍采用菌王觅食算法进行优化计算,以加快收敛速度.分层菌王觅食算法的主要操作流程为:
1) 初始化.初始化包括子群体的个数S,每个子群体的细菌数N,细菌的维数D,游动参数Ns,趋向次数Nc,复制次数Nre,迁徙次数Ned,迁徙概率ped,步长C;
2) 设置循环变量.子群体变量h从1循环至S,趋向变量从1循环至Nc,复制变量从1循环至Nre,迁徙变量从1循环至Ned;
3) 底层子群体循环.每个子群体h均按基本算法完成趋向和迁徙操作,按上述复制算法完成复制操作,再从每个子群体中分别得到一个最优细菌个体(即底层子菌王),共S个底层子菌王个体,由此完成底层循环.
4) 顶层群体循环.用得到的S个底层子菌王构成顶层群体,仍按基本算法完成趋向和迁徙操作,按上述复制算法完成复制操作,由此得到顶层群体的最优个体(即顶层菌王),算法结束.
下面选用3个典型BenchMark测试函数来验证HKBFO算法的有效性,分别为:
1)Schaffer函数:
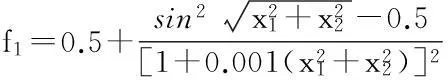
-10≤xi≤10,i={1,2},
其在(0,0)处取得全局最小值0.
2)Ackley函数:
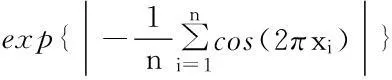
-32 其在(0,0,…,0)处取得全局最小值0. 3)Griewank函数: -600 其在(0,0,…,0)处取得全局最小值0. BFO算法和HKBFO算法中各循环参数的初始值均相同,每个测试函数利用2种算法均计算10次,并取最优解的平均值,寻优精度对比分别见表1—表3. 表1 Schaffer函数对比结果 表2 Ackley函数对比结果 表3 Griewank函数对比结果 2数值模拟 某悬索桥主跨为888m,桥面净宽为33m,加劲梁用扁平单箱单室钢箱梁,矢跨比为1/10.5.主塔塔高为147.5m,两根主缆间距为33m,每根主缆由110股预制平行钢丝索组成.吊索采用骑跨式钢丝绳,间距为12m,每道吊索由4股钢丝绳组成.将该桥的主塔视为底端固定上方自由的支撑杆件,两边锚碇视为固定端.该桥的ANSYS有限元模型如图1所示. 将作用在悬索桥上的车载简化为2个时变力,假定分别为: F1=8000(1+0.1sin(10πt)), F2=10000(1-0.1sin(10πt)). 车辆由桥的左端沿直线匀速移动至桥的右端,沿车辆移动方向看,F1、F2分别代表车辆的前后轮载(单位为N),轴距为3m,移动速度为30m/s,运行路线为距桥面右边11m,直至离开桥面为止,其中, 图1 悬索桥ANSYS有限元模型示意 在桥面上选取9个点,坐标分别为(-222,6.6),(-222,0),(-222,-9.9),(0,6.6),(0,0),(0,-9.9),(222,6.6),(222,0),(222,-9.9)来测量桥面的挠度响应,采样频率为100Hz;用ANSYS数值计算得到的响应替代实测响应.将计算得到的响应作为神经网络的输入向量,以车载数值作为神经网络的输出向量构建测试样本库.再假定车载分别为: 各车载的各个属性与前述相同,同样选取相同的9个坐标位置和采样频率,用得到的相关数据构建训练样本. BP神经网络输入层单元数为9,隐含层单元数取为19,输出层单元数为2,输入层与隐含层之间选取Sigmoid传递函数,隐含层与输出层之间选取线性传递函数,神经网络参数共有230个(9×19+19+19×2+2=230个),即HKBFO算法中细菌个体维数D=230.子群体个数S=20,每个子群体细菌数N=30,趋向次数Nc=30,游动参数Ns=5,复制次数Nre=10,迁徙次数Ned=4,迁徙概率ped=0.25,步长C=0.02.采用相同的初始化参数,依次按照BFO算法和HKBFO算法确定神经网络参数,训练神经网络.将测试样本库带入训练完成后的神经网络,得到车辆荷载识别结果,如图2和图3所示.神经网络正确识别率是指相对误差小于或等于10%的样本数在测试样本集中所占的比例.按照BFO算法和HKBFO算法优化神经网络所得到的车辆荷载识别结果的神经网络正确识别率如表4所示. 图2 HKBFO优化网络识别结果 图3 BFO优化网络识别结果 算法荷载识别率车前轮车后轮BFO64.2870.62HKBFO84.1686.75 3结论 对比图2和图3,再由表4可知,利用HKBFO优化神经网络的识别结果比BFO优化神经网络的识别结果更准确.尽管本文方法得到了更好的识别结果,但仍不够理想,尤其是在车辆荷载上下桥时,其主要原因是:1)神经网络中参数初值是随机给定的,并没有理论依据;2)神经网络中的参数太多,网络拓扑结构过于复杂;3)样本库太过庞大,且样本的典型性和代表性不够好.为此,今后笔者将在参数初值给定和样本选取上作进一步地探讨. 参考文献: [1]田志勇,唐茂林,蒲黔辉.宁波庆丰桥静、动载试验研究[J].桥梁建设,2012,42(5):31-36. [2]欧耀文,周朝阳.某大跨度钢管混凝土拱桥静动载检测、病害及其加固分析[J].郑州大学学报(工学版),2013,34(5):31-37. [3]孔德森,陈永坡,李纯洁,等.液化场地斜直交替群桩-土-桥梁结构动力特性分析[J].山东科技大学学报(自然科学版),2014,33(5):77-82. [4]Law S S,Chan T H T,Zeng Q H. Moving force identification: a time domain method[J]. Journal of Sound and Vibration,1997,201:1-22. [5]Law S S,Chan T H T,Zeng Q H. Moving force identification: a frequency and time domain analysis[J]. Journal of Dynamic Systems,Measurement and Control ASME,1999,12:394-401. [6]Au F T K,Jiang R J,Cheung Y K. Parameter identification of vehicles moving on continuous bridges[J]. Journal of Sound and Vibration,2004,269(12):91-111. [7]陈锋,袁向荣,李明.移动载荷识别的B-样条函数逼近法[J].石家庄铁道学院学报,2003,16(1):11-14. [8]尤琼,史治宇.基于区间B样条小波有限元的移动荷载识别[J].工程力学,2011,28(5):35-40. [9]李忠献,陈锋,王波.基于BP神经网络的桥上移动荷载分阶段识别方法[J].工程力学,2008,25(9):85-92. [10]陈震,余玲.基于截断GSVD方法的桥梁移动荷载识别[J].振动与冲击,2014,33(10):97-100. [11]姜建国,周佳薇,郑迎春,等.一种双菌群细菌觅食优化算法[J].深圳大学学报(理工版),2014,31(1):43-51. [12]Chatzis S P,Koukas S. Numerical optimization using synergetic swarms of foraging bacterial populations[J]. Expert Systems with Application,2011,38(12):15332-15343. [13]梁艳春,吴春国,时小虎,等.群智能优化算法理论与应用[M].北京:科学出版社,2009:157-159. [14]金敏,鲁华祥.一种遗传算法与粒子群优化的多子群分层混合算法[J].控制理论与应用,2013,30(10):1231-1238.