一类二阶q-对称差分方程两点边值问题解的存在性

*通信作者：侯成敏(1963—)，女，教授，研究方向为微分方程与离散动力系统.

一类二阶q-对称差分方程两点边值问题解的存在性

徐佳宁，龚学，吴凡，侯成敏*

( 延边大学理学院 数学系，吉林 延吉 133002 )

摘要：研究了一类二阶q-对称差分方程两点边值问题解的存在性.首先,利用Bananch空间压缩映像原理获得了解的存在唯一性结果；其次，在一定的边界条件下，通过假设非线性项具有超线性和次线性性，建立了该问题存在正解的充分性条件.

关键词：q-对称差分方程； 边值问题； 不动点； 超线性和次线性

收稿日期：2015-06-07

文章编号：1004-4353(2015)03-0189-07

中图分类号：O175

Existence of solutions for a class ofq-symmetric difference equation two points boundary value problem

XU Jianing,GONG Xue,WU Fan,HOU Chengmin*

(DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,China)

Abstract：We considered the existence of solutions for a class of the two points boundary value problem of q-symmetric difference equation. First,we obtained the existence and uniqueness of solutions by using the generalized Banach contraction principle. Then under some boundary value conditions,sufficient conditions of existence of positive solutions are established in both the superlinear and sublinear cases.

Key words：q-symmetric difference equation; boundary value problem; fixed point; superlinear and sublinear

0引言

2010年，M.El-Shabed等[1]研究了二阶差分方程边值问题:

-u″=a(t)f(u(t)),0≤t≤1;

(1)

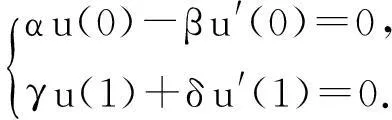
(2)

其中函数f,a以及式(2)中的常系数满足一定的条件.在超线性和次线性的情况下，M.El-Shabed等建立了问题(1)—(2)正解的存在性条件.2013年，Yang Wengui[2]研究了如下q-差分方程的边值问题:

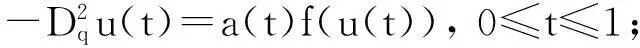
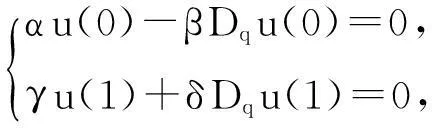
利用压缩映射原理及锥的伸拉缩定理获得了其正解的存在性.受上述工作启发，本文考虑如下二阶q-对称差分方程的边值问题:

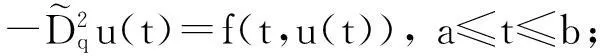
(3)

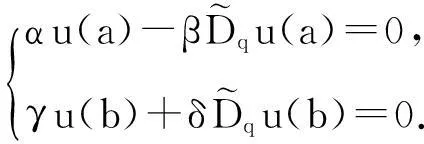
(4)

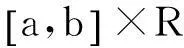
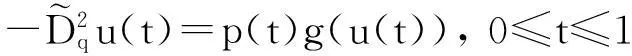
(5)

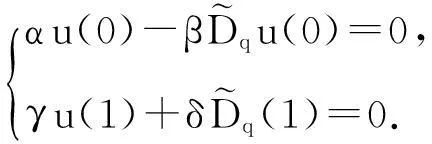
(6)

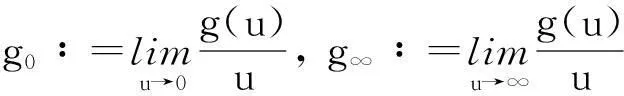
1预备知识

假设q∈(0,1)，则称B是(q,q-1)-几何的，如果对每一个x∈B，有qx,q-1x∈B.

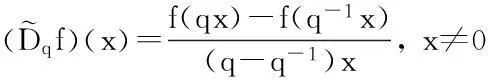
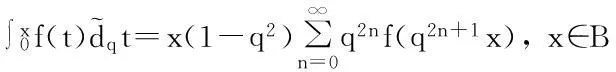
莱布尼兹公式和q-对称分部积分公式分别为：

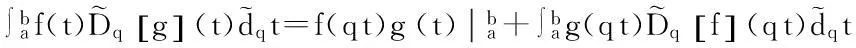
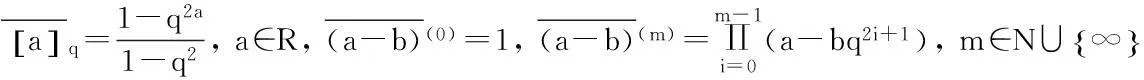
引理1[12]设X是一个巴拿赫空间，T∶X→X是一个完全连续算子，并且符合V={u⊂X|u=μTu,0<μ<1}是有界的，则T在X中有一个不动点.

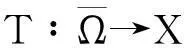
证明首先,考虑a=0时的情形.由定义2，有：

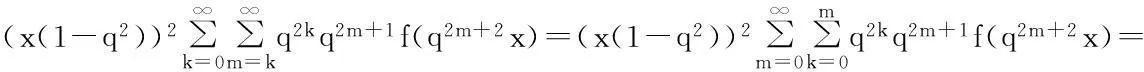
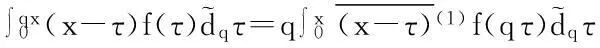
其次，考虑a≠0时的情形.由定义2，并利用a=0时的结论有

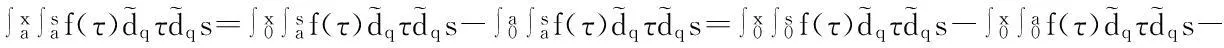
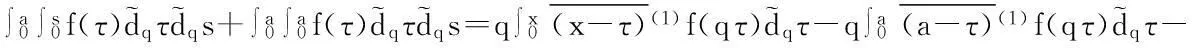
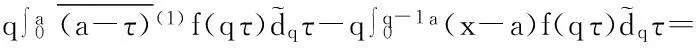
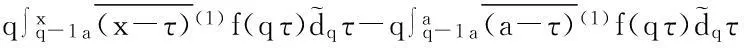
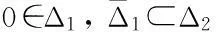
1) ‖Ax‖≤‖x‖,∀x∈K∩∂Δ1且‖Ax‖≥‖x‖,∀x∈K∩∂Δ2;

2) ‖Ax‖≥‖x‖,∀x∈K∩∂Δ1且‖Ax‖≤‖x‖,∀x∈K∩∂Δ2.

2格林函数及存在性定理

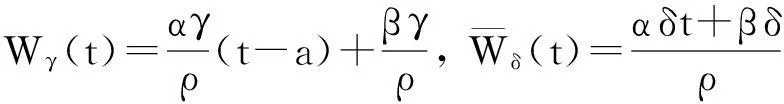
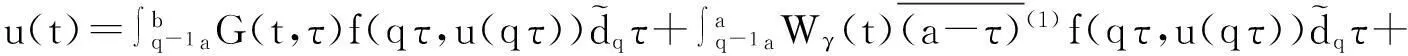
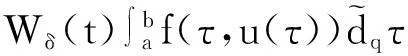
证明,则.由边界条件(4),有：

αC2-βC1=0,

(7)

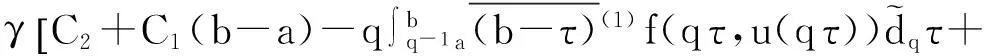
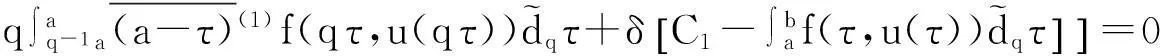
(8)

解方程(7)—(8),得

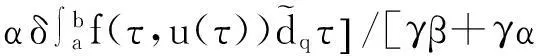
于是有

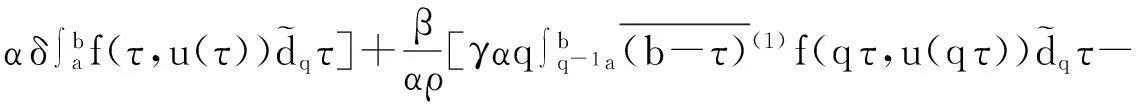
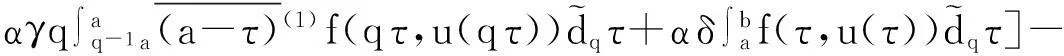
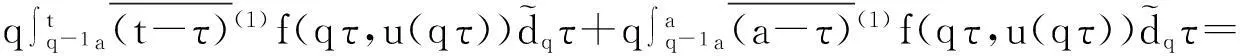
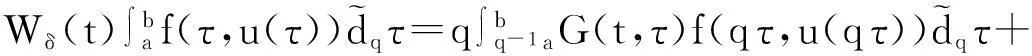
推论1边值问题(5)—(6)的解为

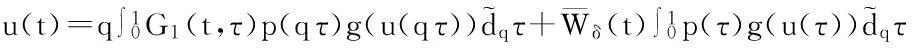
(9)

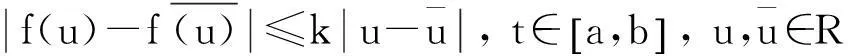
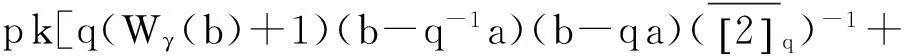
(10)

则边值问题(3)—(4)在[a,b]上有唯一解.

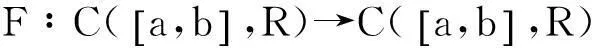
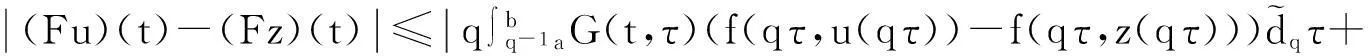
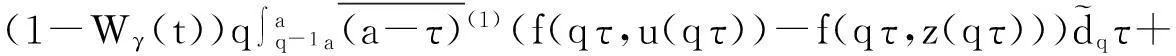
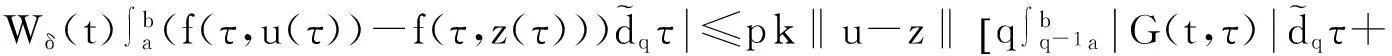
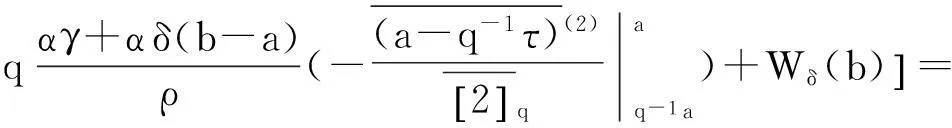
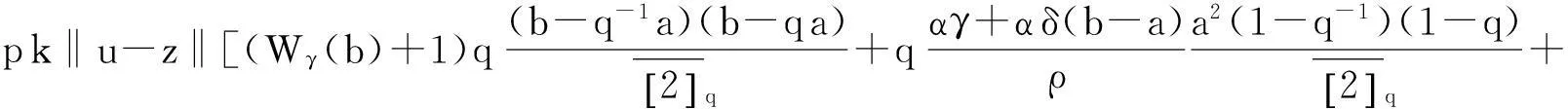
Wδ(b)(b-a)]<1.

由条件(10)知F是一个压缩映射，因此存在唯一的不动点,即边值问题(3)—(4)有唯一解.

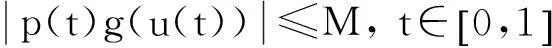
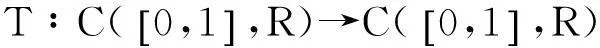
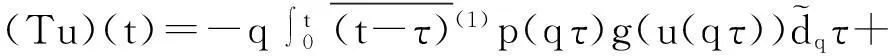
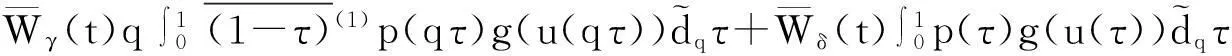
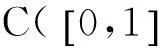
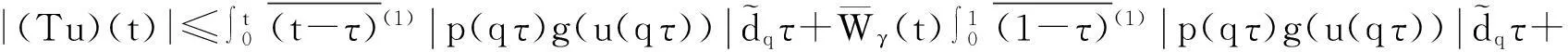
由此证明了‖(Tu)(t)‖≤M2.

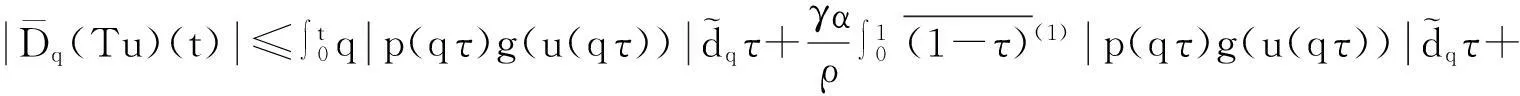
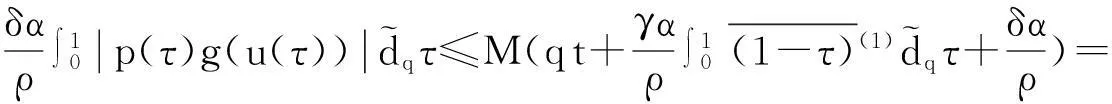
通过以上证明，再由引理2知，算子T至少有一个不动点，由此证明了问题(5)—(6)至少有一个解.

证明，又因G1(1,τ)=0，所以.当τ>t时，

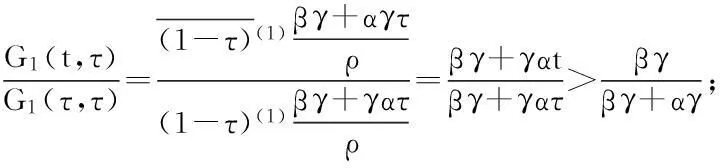
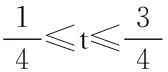
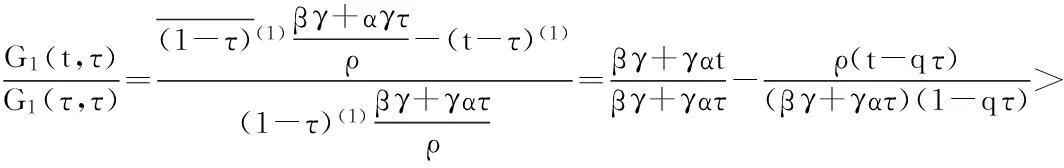
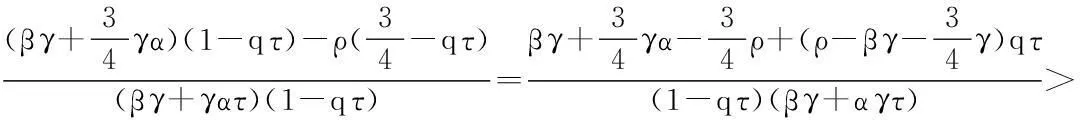
引理7A是一个正算子，即A(K)⊂K时u∈K.

证明显然Au(t)≥0,利用引理6得

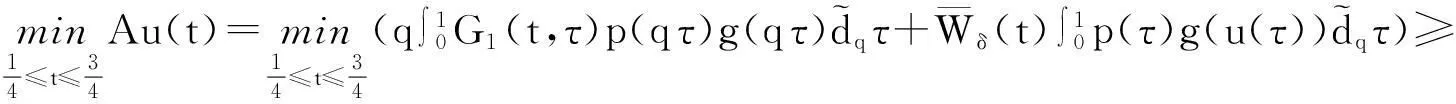
定理3问题(5)—(6)在超线性和次线性的情况下至少存在一个正解.

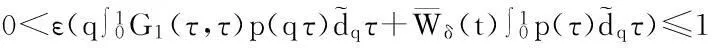
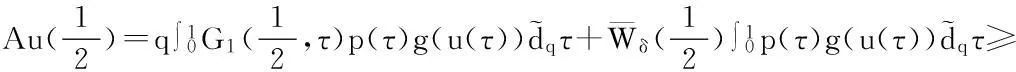
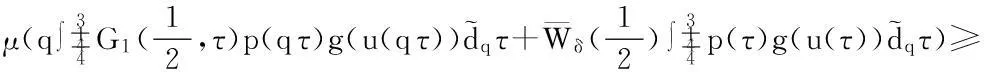
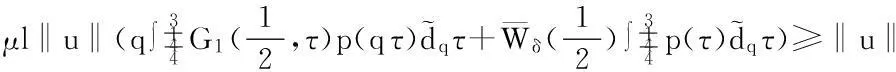
由此证明了当u∈K∩∂Δ2时，‖Au‖≥‖u‖.

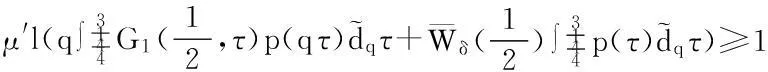
综上，当u∈K且‖u‖=δ2′时，可得到‖Au‖≤‖u‖,u∈K∩∂Δ2′，由此得出A有一个不动点.

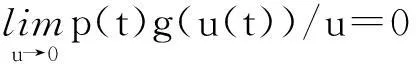
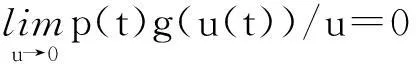
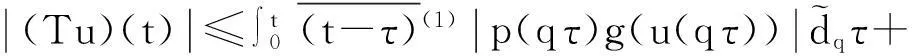
参考文献：

[1]El-ShabedM,HassanHA.Positivesolutionsofq-differenceequation[J].ProcAmerMathSoc,2010,138:1733-1738.

[2]YangWengui.Anti-periodicboundaryvalueproblemsinvolvingnonlinearfractionalq-differenceequations[J].MalayaJournalofMatematik,2013,4(1):107-114.

[3]JacksonFH.Onq-funtionsandacertaindifferenceoperator[J].TransRoySocEdin,1908,46:253-281.

[4]JacksonFH.Onq-definiteintegrals[J].QuartJPureandApplMath,1910,41:193-203.

[5]StromingerA.Informationinblackholeradiation[J].PhysRerLett,1993,71:3743-3746.

[6]YoumD. q-Deformedconformalquantummechanics[J].PhysRevD,2000,62:095009.

[7]LavagnoA,SwamyNP. q-Deformedstructuresandnonextensivestatistics:acomparativestudy[J].PhysicaA:StatisticalMechanics&ItsApplications,2002,305(1):310-315.

[8]BooleG.CalculusofFiniteDifferences[M].NewYork:ChelseaPublishingCompany,1957.

[9]ErnstT.Thedifferenttonguesofq-calculus[J].ProcEstAcadSci,2008,57(2):8199.

[10]KacV,CheungP.QuantumCalculus[M].NewYork:Springer,2002.

[11]KoekockR,LeskyPA,SwarttouwRF.HypergeometricOrthogonalPolynomialsandTheirq-Analogues[M].Berlin:SpringerMonographsinMathematics, 2010.

[12]SmartDR.FixedPointTheorems[M].Cambridage:CambridageUniversityPress,1980.