基于阈值改进的小波变换在高铁变形分析中的应用

袁明月，文鸿雁，周　吕，陈冠宇(桂林理工大学a.广西矿冶与环境科学实验中心; b.测绘地理信息学院; c.广西空间信息与测绘重点实验室，广西桂林　541004)



基于阈值改进的小波变换在高铁变形分析中的应用

袁明月，文鸿雁，周吕，陈冠宇
(桂林理工大学a.广西矿冶与环境科学实验中心; b.测绘地理信息学院; c.广西空间信息与测绘重点实验室，广西桂林541004)

摘要:对小波变换阈值函数算法进行了改进，并实现了高铁变形数据的去噪处理，使得去噪后均方根误差相对于改进前明显减小，信噪比相对于改进前明显增大，改进效果明显。算例表明，用Kalman滤波模型对改进阈值函数小波去噪结果进行预测，预测效果较好，说明本文改进方法是一种有效的去噪方法，可以用于建筑物变形分析预处理。

关键词:小波变换;阈值;去噪;变形分析; Kalman滤波

小波变换是一种时－频分析方法，具有低熵性、多分辨率、去相关性和选基灵活性的特点，小波去噪是低通滤波和特征提取的结合，去噪效果明显。1995年D. L. Donoho提出阈值法小波去噪，包括硬阈值和软阈值法［1］。为了克服传统阈值法的缺点，本文在软、硬阈值法去噪的基础上，提出了一种改进阈值函数去噪方法，并对某高铁一监测点实测沉降变形数据进行去噪实验，即用小波变换对变形信号进行消噪，提取信号。结果证明，该改进阈值函数滤波方法较传统阈值函数法有更好的滤波效果。

1　小波变换去噪

1. 1小波阈值法去噪

小波阈值法去噪的基本思想是:选择合适的阈值对小波函数分解后的信号进行处理，使低于该阈值的小波系数变为零，当高于或等于该阈值时，将对应的小波系数予以保留，从而使信号中的噪声得到有效抑制［2］。

阈值函数是对小波系数进行处理的方法，包括硬阈值法、软阈值法。

设对叠加了高斯白噪声的有限长度信号，某尺度j时小波变换系数yj= Ajf( x)可表示为

其中: xj为原始信号的小波变换系数; zj为一个标准的高斯白噪声，服从正态分布。

硬阈值法:

软阈值法:

1. 2阈值函数改进算法

软、硬阈值法虽然都得到广泛应用，但是此方法也有不足之处，如:硬阈值函数的不连续性使得重构信号产生振荡;在软阈值中| yj|＞δ时，^xj与yj总存在恒定偏差，并且因为减小了绝对值大的小波系数，还会导致信号边缘模糊。基于上述考虑，本文在传统阈值函数法的基础上对阈值函数进行了改进，其改进表达式如下:

式中，a∈［0，1］为可变参数。

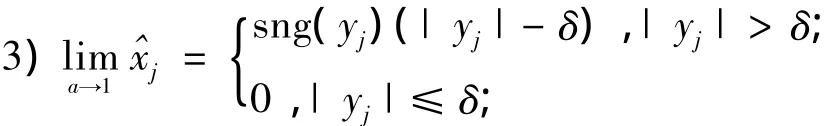
4)当a = 1时，阈值函数等效于软阈值函数。由以上分析以及图1可知，参数a取不同的值，改进阈值函数的发展方向会呈现不同的趋势，但始终是一条不间断的折线: a = 0时，改进阈值函数曲线包括硬阈值函数的曲线;当a = 1时，改进阈值函数曲线即为软阈值函数曲线。该方法既解决了软阈值函数产生恒定偏差的问题，又克服了硬阈值函数不连续的问题，新阈值函数兼有软、硬阈值函数的优点，可以通过调节a，直至达到最佳去噪效果。

由图2可知随a的增大，信噪比曲线先增大后减小，因此选择合适的参数才能达到最优的去噪效果。结合信噪比、信号均方差、光滑度等方面选择a =0. 011时的滤波为最优滤波。

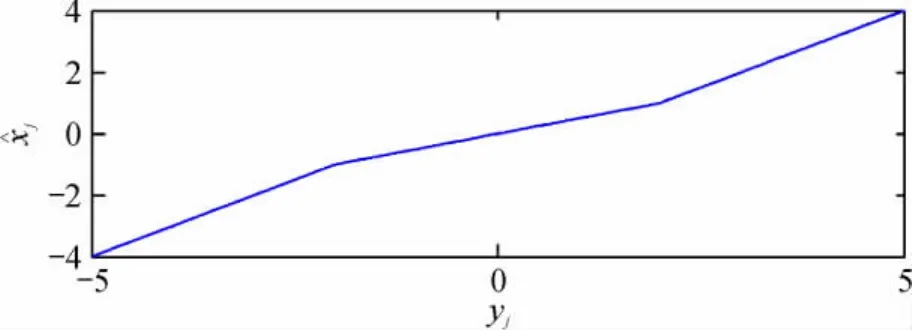
图1　改进阈值函数(其中a =0.5，δ=2)Fig. 61Improved threshold function ( a =0.5，δ=2)

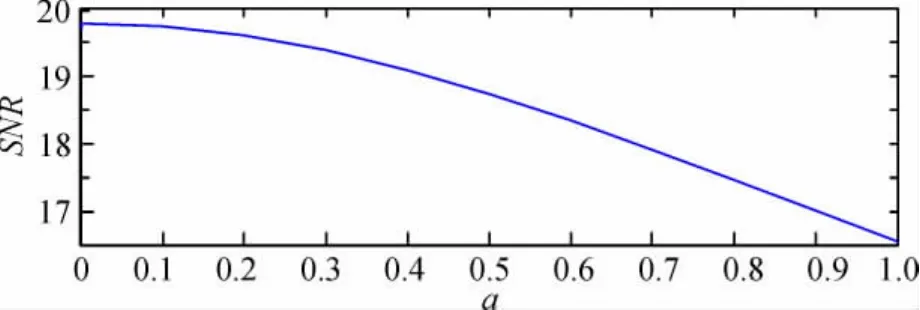
图2　改进阈值法不同参数a的信噪比Fig. 62SNR of improved threshold method by different a

2　Kalman滤波模型的建立

对于离散时间线性随机系统的卡尔曼滤波，其数学模型由状态方程与观测方程构成，离散化形式可以表示为［2］

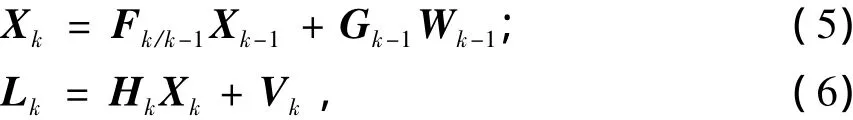
式中: Xk为系统k时刻的状态向量; Fk/k－1为系统从k－1时刻到k时刻的状态转移矩阵; Gk－1为系统k－1时刻的动态噪声矩阵; Wk－1为系统k－1时刻的动态噪声，其协方差矩阵为Qk; Lk是系统k时刻的观测向量; Hk是系统k时刻的观测矩阵; Vk为系统k时刻的观测噪声，其协方差为Rk。

根据最小二乘原理，推出随机离散线性系统的Kalman滤波递推公式［2］:

状态向量的一步预测

状态向量的一步预测方差阵

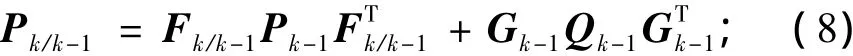
状态向量的估计值

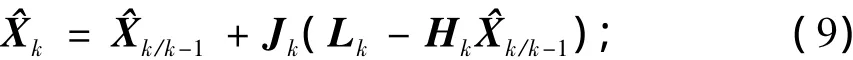
状态向量的估计值的方差矩阵

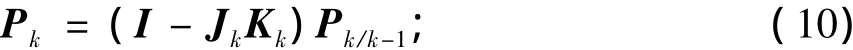
J是滤波增益矩阵

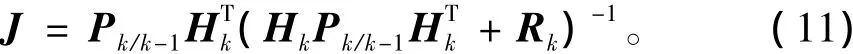
式中，Rk是系统的观测噪声方差阵。

Kalman滤波是一种动态数据处理方法，其滤波方程是一组递推计算公式，计算过程是不断预测、修正的过程，特别适合变形监测数据的动态处理［3］。

3　应用实例

3. 1小波去噪

以某高铁一监测点变形监测数据为例，基于Matlab软件平台下编程实现小波去噪，本文采用了db4小波，对信号进行了4层分解，用软、硬阈值以及改进阈值函数3种方法进行去噪。去噪曲线与实测值曲线比较如图3～图5所示。图3表明，软阈值法得到的去噪信号比较光滑，但将一些有用的信号当作随机噪声被滤掉，失真较大，边缘比较模糊，滤波效果不佳;图4表明，硬阈值法去噪后得到的曲线保留了一些有规律起伏变化信息，效果优于软阈值;从图5可以看出，改进阈值函数去噪曲线与原始信号曲线更逼近，能真实地反映变形趋势，滤波效果较好。总体上，改进阈值函数去噪曲线与原始信号的曲线的逼近程度较软、硬阈值函数法更高，即信号特征保留的更加完整，能更真实的反映变形情况。

为了从数值上说明改进阈值函数法去噪效果，比较几种方法的信噪比( SNR)与均方根误差( RMSE)，如表1所示。

可以看出，软阈值函数法信噪比为18. 339 5，低于硬阈值函数法，而改进阈值函数法信噪比最高为19. 775 7，且改进阈值函数法的去噪信号均方差最小为0. 097 4，硬阈值函数法以及软阈值函数法均高于改进阈值函数法。以上表明，改进阈值函数具有更好滤波精度，去噪效果较佳，在变形监测数据处理方面具有较好的应用价值。

3. 2 Kalman滤波模型预测

基于上节小波改进阈值法滤波结果进行变形分析预测。首先利用Kalman滤波模型分别对小波改进阈值法滤波结果以及原始数据的前41期数据建模进行拟合，后5期作为预测序列，然后对比模型预测效果，结果如图6、图7所示。

可以看出，Kalman滤波模型对小波改进阈值法滤波结果以及原始数据的拟合效果都比较好，但是对小波改进阈值法滤波结果的拟合效果更好、预测精度更高;改进阈值函数小波去噪是对变形信号进行消噪，使信号特征保留的更加完整，能够更真实的反映变形情况，有利于对后期进行变形分析与预测，提高预测精度。

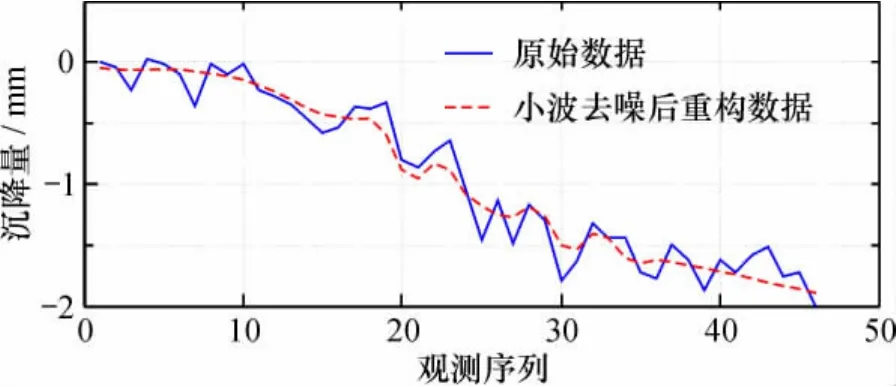
图3　软阈值函数法处理结果与原始数据对比Fig. 63Comparison of soft threshold function method and original data

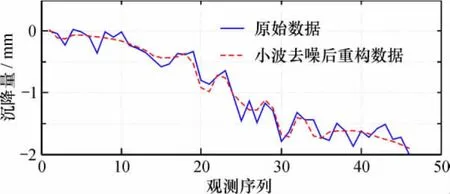
图4　硬阈值函数法处理结果与原始数据对比Fig. 64Comparison of hard threshold function method and original data

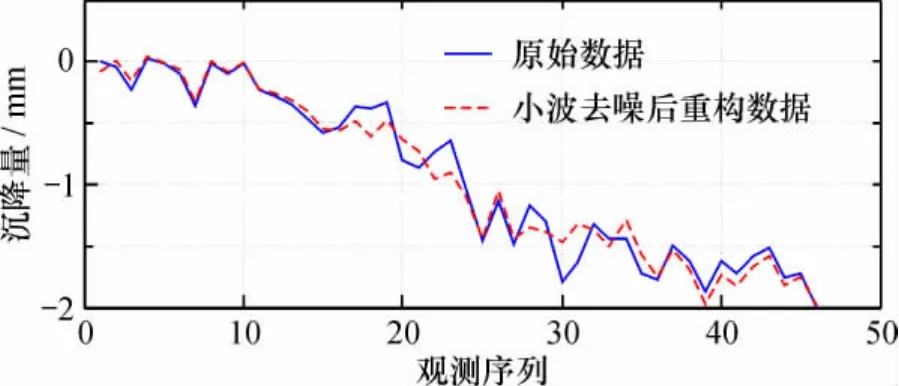
图5　改进阈值函数法处理结果与原始数据对比Fig. 65Comparison of improved threshold function method and original data

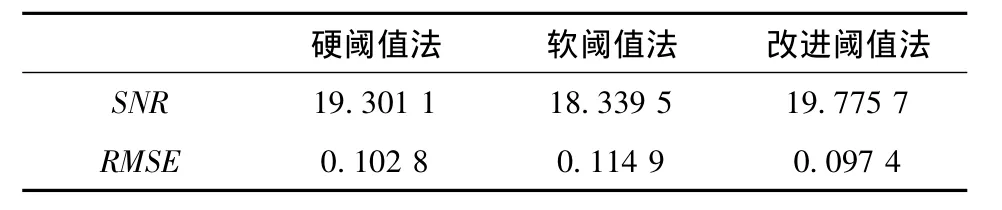
表1　3种阈值法去噪的均方根误差与信噪比Table 1　RMSE and SNR of denoising in three threshold methods

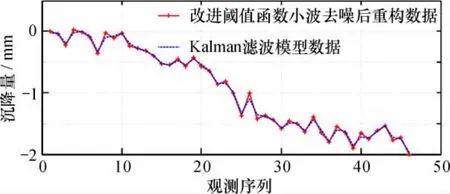
图6　改进阈值函数法处理结果与经Kalman滤波模型拟合、预测值对比Fig. 66Comparison of improved threshold function method and values and predictions of Kalman filtering model

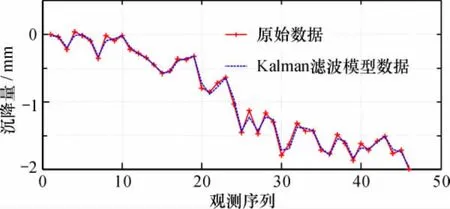
图7　原始数据与经Kalman滤波模型拟合、预测值对比Fig. 67Comparison of original data and values and predictions of Kalman filtering model

本文采用后验差检验法中的后验差比值C和小误差概率P对模型的精度进行评判，评判结果如表2所示。

表2　两种Kalman滤波模型预测模型的精度对比表Table 2　Comparison of precision of two methods

由模型的精度表2可知，两个模型的预测精度均能够达到一级，且小误差概率达到100%，但对小波改进阈值法滤波结果的后验差比值是对原始数据预测结果的后验差比值的84. 5%，说明基于改进阈值法去噪后的数据进行变形分析预测可信度更高，具有更好的优越性和应用价值。

4　结论

本文提出了一种对传统小波改进阈值函数的算法，并用MATLAB编程实现软、硬阈值函数与改进阈值函数法去噪。实验结果证明:

( 1)改进阈值函数法与传统软、硬阈值函数法相比，有效地抑制了信号波形失真，去噪曲线与原始数据曲线更加逼近，具有更好的可信度。

( 2)从信噪比和均方根误差的角度看，改进阈值函数法信噪比最高，原始信号与估计信号的均方根误差最小，消噪信号更接近于原始信号，能够有效地识别信号和噪声，较好地消除噪声并且保留特征信号，去噪效果明显改善，适合于变形监测数据的去噪处理，具有很好的应用价值。

( 3)用Kalman滤波模型对改进阈值函数法处理结果的后5期进行预测，预测效果更好，证明本文的改进阈值函数法有效并具有可行性，可以作为在变形分析预测中的一种数据预处理方法。

参考文献:

［1］李弼程，罗建书．小波分析及其应用［M］．北京:电子工业出版社，2003: 165－169．

［2］朱云芳，戴朝华，陈维荣．小波消噪阈值选取的一种改进方法［J］．电测与仪表，2005，42 ( 7) : 4－6．

［3］文鸿雁，张正禄．非线性小波变换阈值法去噪改进［J］．测绘通报，2006 ( 3) : 18－21．

［4］陈冠宇，文鸿雁，周吕，等．基于Kalman滤波下的高铁隧道沉降变形评估方法［J］．桂林理工大学学报，2013，33 ( 4) : 671－676．

［5］文鸿雁．小波多分辨分析在变形分析中的应用［J］．地壳形变与地震，2000，20 ( 3) : 27－32．

［6］文鸿雁，张正禄．小波分析与傅里叶变换相结合在探测周期性变形中应用［J］．测绘通报，2004 ( 4) : 14－16．

［7］王磊，张福海，王纲，等．高铁桥梁下明挖隧道施工安全分析［J］．施工技术，2013，42 ( 5) : 72－74，106．

［8］徐宁寿．随机信号估计与系统控制［M］．北京:北京工业大学出版社，2001: 135－154．

［9］钱曾波，朱述龙．基于小波变换的图像变焦技术［J］．解放军测绘学院学报，1994，11 ( 3) : 171－174．

［10］江世宏．MATLAB语言与数学实验［M］．北京:科学出版社，2007．

Application of high-speed railway deformation analysis based on improved wavelet threshold value

YUAN Ming-yue，WEN Hong-yan，ZHOU Lyu，CHEN Guan-yu
( a. Guangxi Scientific Experiment Center of Mining，Metallurgy and Environment; b. College of Geomatics and Geoinformation; c. Guangxi Key Laboratory of Spatial Information and Geomatics，Guilin University of Technology; Guilin 541004，China)

Abstract:An improved algorithm of wavelet transform threshold function is proposed，by the denoising processing of high-speed rail deformation data．Compared with previous methods，this algorithm reduces the denoising a lot．When RMSE is decreased，the signal-to-noise is obviously increased．A prediction is made for the improved threshold function wavelet denoising by Kalman filter model．This improved method is proved to be an effective denoising method and can be applied to the pretreatment of the building deformation analysis．

Key words:wavelet; the threshold value; denoising; deformation; Kalman filter

通讯作者:文鸿雁，博士，教授，glitewhy@163. com。

作者简介:袁明月( 1990—)，女，硕士研究生，研究方向:变形监测与数据处理，770695716@ qq. com。

基金项目:国家自然科学基金项目( 41461089) ;广西“八桂学者”专项经费项目;广西空间信息与测绘重点实验室项目(桂科能130511402; 1207115－06) ;广西自然科学基金项目( 2014GXNSFAA118288) ;广西矿冶与环境科学实验中心项目( KH2012ZD004) ;广西研究生教育创新计划项目( YCSZ2014151; YCSZ2012083)

收稿日期:2014－03－11

doi:10. 3969/j．issn. 1674－9057. 2015. 01. 016

文章编号:1674－9057( 2015) 01－0107－04

文献标志码:A

中图分类号:P228

引文格式:袁明月，文鸿雁，周吕，等．基于阈值改进的小波变换在高铁变形分析中的应用［J］．桂林理工大学学报，2015，35 ( 1) : 107－110．