双涡卷Jerk非线性系统混沌电路设计
2016-01-07陈娇英彭宇宁唐英姿广西大学电气工程学院南宁50004广西工业职业技术学院南宁5000广西师范学院南宁5000
陈娇英,彭宇宁,唐英姿( .广西大学电气工程学院,南宁 50004; 2.广西工业职业技术学院,南宁 5000; .广西师范学院,南宁 5000)
双涡卷Jerk非线性系统混沌电路设计
陈娇英1,2,彭宇宁1,唐英姿3
( 1.广西大学电气工程学院,南宁530004; 2.广西工业职业技术学院,南宁530001; 3.广西师范学院,南宁530001)
摘要:为进一步探讨非线性混沌系统的可控规律,实现对混沌现象的利弊进行有效控制,根据双涡卷Jerk混沌系统状态方程,采用模块化电路设计理论设计了双涡卷Jerk非线性混沌电路,并使用Matlab软件仿真其数学模型,Multisim软件仿真其硬件电路。仿真结果证明:设计的双涡卷非线性混沌电路能产生与数学模型仿真结果一致的混沌波形,验证了所设计双涡卷Jerk混沌电路的正确性。
关键词:非线性系统;双涡卷Jerk混沌电路;模块化电路设计理论
混沌系统是一门交叉学科,属于物理、数学和控制的交叉研究领域[1]。混沌自20世纪90年代以来一直都是非线性学科研究的热点。正如人类如果没有发现“黑色黄金”——石油的价值所在,今天就不会拥有如此发达的交通工具——飞机;如果人类没有认识到电磁感应现象,就不会有现在的万家灯火和高科技。混沌现象广泛存在于各种非线性控制系统中。广泛地发现混沌现象,探索新型混沌系统,用电子器件构造和演示混沌现象,做出典型混沌系统的实物模型,在演示器上寻找和研究混沌系统控制方法,通过模拟寻求共性,实时控制趋利避害,具有一定的现实意义和实用价值。
笔者采用直接观测法[2]对混沌系统进行研究,分析混沌现象产生的原因及原理,通过动力学系统的数值和器件仿真相轨迹在相空间中随时间的变化及状态方程中变量随时间的走向,对数值器件仿真和硬件电路图产生的混沌相图进行对比,总结混沌的规律。用模块化电路设计方法设计双涡卷Jerk非线性系统混沌电路,从仿真结果相图中观察变量运动的轨迹,得到完整清晰的双涡卷Jerk混沌波形。
1 双涡卷Jerk混沌系统数学模型
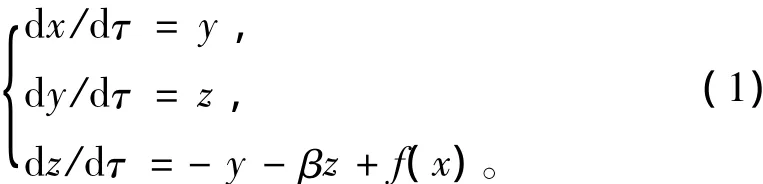
双涡卷Jerk非线性混沌系统是2000年美国科学家J C Sportt提出来的[3-4],其无量纲状态方程为式中的各参数取值:β为0. 45~0. 7,x、y、z、τ均为无量纲变量。当式f( x) = | x |-1时,该状态方程将产生单涡卷混沌现象;而当f( x) = sgn( x)-x时,该状态方程将产生双涡卷混沌现象。非线性函数f( x) = sgn( x)-x为锯齿波,而F( x) = sgn( x)是阶梯波,由此可知锯齿波和阶梯波其实只是通过增加或者减少一个线性函数便可以实现两者之间的相互转换。如果将锯齿波的函数f( x) = sgn( x)-x改成由阶梯波函数F( x) = sgn( x)来代替,则式( 1)变换为

2 数学模型Matlab仿真
利用Matlab软件对双涡卷Jerk系统的数学表达式式( 2)进行仿真(取β= 0. 5)。在仿真前需要对仿真时间T、步长Step和双踪示波器的坐标范围进行适当的调整,以便对波形进行观察和分析。
从图1所示的仿真波形可以观察到清晰的双涡卷混沌波形。在双涡卷系统数学模型仿真中发现,虽然β在0. 45~0. 7间任意取值时产生的波形有所不同,但是都能产生稳定相似的混沌波形;如果β的取值不在此范围内,将不会产生混沌波形,而会产生以下的两种情况:
①当β<0. 45时仿真的波形将向外发散,无法形成稳定的混沌波形;
②当β>0. 7时,仿真的波形将由外向内运动逐渐终止,最后也无法形成稳定的混沌波形。
可见,混沌系统参数对混沌系统的初值有决定性作用。如果系统各参数取值不当或者有微小的变化,随着混沌轨迹的不断变化将会产生巨大偏差,最终将不能产生标准的混沌波形或者波形将消失。参数取值的不同对混沌造成的影响,证明了混沌系统的可控性。混沌系统表面看上去都是一些无规则、杂乱无章的运动轨迹,并没有什么规律可言,但其系统内部是遵循一定的规律的,运动轨迹始终在一定范围内作非线性运动,似乎有一种无形的吸引力在约束它。对此可以利用混沌现象原理对一些非线性系统进行控制,利用类似“混沌吸引子”系统将难以控制的非线性动力学控制在安全稳定的范围之内,使之发挥有利作用,同时去除造成危害的部分。

图1 双涡卷Jerk系统数学模型仿真波形Fig. 61Jerk system state equation simulation phase diagram
3 双涡卷Jerk混沌电路的设计
采用模块化电路设计方法[5-9],设计过程主要分为3个步骤。
1)进行变量的比例压缩变换。通常所用的运算放大器芯片的电源电压为±15 V,而运算放大器的线性动态范围是±13. 5 V,所以首先利用Matlab对该系统进行仿真,观察该系统相图中的变量是否超出线性动态范围(±13. 5 V)。如果没有超出这个范围,则该系统无量纲方程不需要作比例压缩变换;如果超出这个范围就需要作变量比例压缩变换。在对双涡卷系统的状态方程进行数学仿真过程中可以观察到图1中各相图的变量变化范围都没有超过运算放大器±13. 5 V的动态范围,因此在进行电路设计时不需要对状态方程作变量比例压缩。
2)作时间尺度的变换、微分-积分转换、标准化处理。对状态方程进行积分-微分的转换及时间尺度的变换,然后将积分方程标准化,得到的状态方程:

其中: R0、C0为积分时间常数; f( x) = sgn( x)-x为非线性函数,其模块电路设计如图2所示。
3)根据标准积分方程设计出相应的模块化电路。系统模块化电路设计如图3所示。运算放大器采用LF353P型号,芯片采用±15 V双电源供电方式;电阻采用固定阻值的电阻和可调电位器,主要是方便对电路中的可调系数进行调整,同时通过对可调电位器的调整探索参数变换对于整个混沌系统的影响。

图2 非线性函数电路图Fig. 62Diagram of nonlinear function circuit
4 系统电路Multisim仿真
在Multisim仿真软件中,对图3双涡卷Jerk系统电路进行仿真。电容采用无极性电容。电路及元件参数见图3。仿真结果在泰克示波器上输出(图4),输出波形图见图5。
将电路输出的混沌波形与Matlab数值仿真的混沌波形图1进行对比,结果表明两种仿真的波形是一致的,说明所设计的电路是正确的。

图3 双涡卷Jerk系统模块电路图Fig. 63Jerk system module circuit diagram

图4 双涡卷Jerk混沌系统硬件电路3个输出端波形仿真Fig. 64Three output waveform simulation of Jerk system hardware circuit
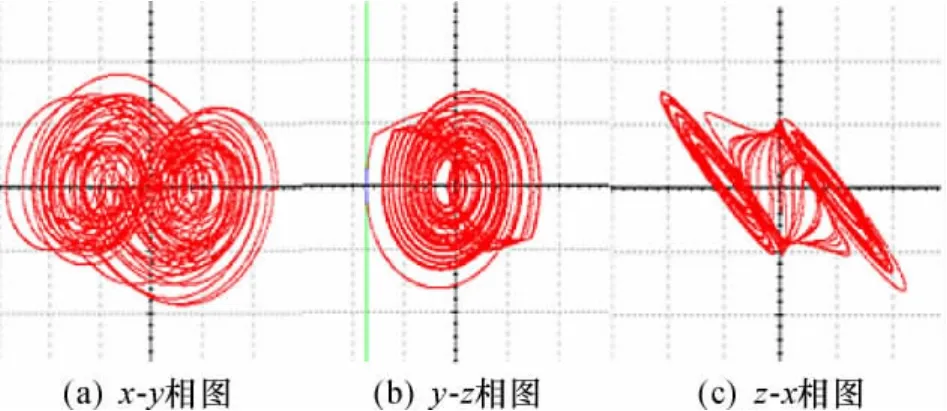
图5 双涡卷Jerk混沌系统硬件电路仿真Fig. 65Jerk system hardware circuit chaos waveforms phase diagram
5 结论
本文研究了双涡卷Jerk混沌系统模块化电路的设计方法。通过Matlab数值仿真、Multisim器件仿真的对比,找出了混沌系统的一般规律以及参数取值的不同对混沌造成的影响,证明了双涡卷Jerk混沌系统的可控性。对非线性控制领域发掘更多新的混沌系统和混沌现象,对混沌的利弊实现有效控制,减少混沌现象对人类的影响有一定参考价值。特别是就电力系统而言,掌握对混沌现象的控制方法和手段、探索混沌现象的应用前景具有很大的实际意义。
参考文献:
[1]Agiza H N,Yassen M T.Synchronization of Rossler and Chen chaotic dynamical systems using active control[J].Physics Letters A,2001,278 ( 4) : 191-197.
[2]Ma C Y,Wang L S,Yin Z,et al.Sliding mode control of chaos in the noise-perturbed permanent magnet synchronous motor with non-smooth air-gap[J].Mining Science and Technology ( China),2011,21 ( 6) : 835-838.
[3]Yu J P,Chen B,Yu H S,et al.Adaptive fuzzy tracking control for the chaotic permanent magnet synchronous motor drive system via backstepping[J].Nonlinear Analysis: Real World Applications,2011,12 ( 1) : 671-681.
[4]Li T Y,Yorke J A.Period three implies chaos[J].The A-merican Mathematical Monthly,1975,82 ( 10) : 985-992.
[5]禹思敏.混沌系统与混沌电路[M].西安:西安电子科技大学出版社,2011.
[6]黄曼磊,刘宏达,许梦琪.柴油发电机组并联运行的混沌振荡分析[J].哈尔滨工程大学学报,2012,33 ( 2) : 192-196.
[7]王学梅,张波.H桥直流斩波变换器边界碰撞分岔和混沌研究[J].中国电机工程学报,2009,29 ( 9) : 22-27.
[8]刘崇新.一个超混沌系统及其分数阶电路仿真实验[J].物理学报,2007,56 ( 12) : 6865-6873.
[9]孙连新,王忠林,韩敬伟.一个新的三维混沌系统分析及电路实现[J].四川兵工学报,2010,31( 2) : 116-118.
Chaotic circuit design for double turbination Jerk nonlinear system
CHEN Jiao-ying1,2,PENG Yu-ning1,TANG Ying-zi3
( 1. College of Electrical Engineering,Guangxi University,Nanning 530004,China; 2. Guangxi Vocational and Technical Institute of Industry,Nanning 530001,China; 3. Guangxi Normal Institute,Nanning 530001,China)
Abstract:In order to explore the control rule of nonlinear chaotic system and realize the pros and cons of chaos phenomenon under effective control,based on double turbination Jerk chaos system state equation,and the theory of modular circuit design,double turbination Jerk nonlinear chaotic circuit is introduced,its mathematical model by Matlab software simulation,Multisim software simulation of hardware circuit.The simulation results prove that the design of double turbination nonlinear mathematical model for the simulation results is in agreement with the chaotic circuit and can produce chaotic waveform.The correctness of the design of double turbination Jerk chaotic circuit has also been verified,with reference for the control and application of the chaotic phenomenon in the future.
Key words:modular circuit design theory; dual-scroll chaotic nonlinear phenomena demonstrator; Matlab and Multisim simulation
作者简介:陈娇英( 1966—),女,硕士,副教授,研究方向:电力系统分析与控制,cjy-6647@163. com。
基金项目:广西自然科学基金项目(桂科基0663022)
收稿日期:2014-12-08
doi:10. 3969/j.issn. 1674-9057. 2015. 01. 035
文章编号:1674-9057( 2015) 01-0213-04
文献标志码:A
中图分类号:TM13
引文格式:陈娇英,彭宇宁,唐英姿.双涡卷Jerk非线性系统混沌电路设计[J].桂林理工大学学报,2015,35( 1) : 213-216.
