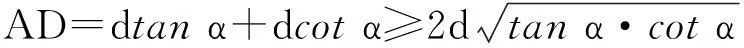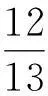问题解决循环模式下的高中物理一题多解

问题解决循环模式下的高中物理一题多解

张建斌柴春琪

(嘉兴市第一中学 浙江 嘉兴314050)

摘 要：本文根据斯滕伯格的问题解决循环模式，简述基于一题多解的高中物理问题解决循环模式及其应用，并结合一题多解培养学生的问题解决能力.

关键词：问题解决高中物理一题多解

收稿日期：(2014-12-12)

现代认知心理学认为问题解决是人在没有明显的解决方法的情况下,将给定情境转化为目标情境的认知过程,也就是问题解决是有目的的认知活动.问题解决具有以下3个基本特性:(1)目的的指向性,问题解决具有明确的目的性,问题解决活动必须是目的指向的活动,它总是要达到某个特定的终结状态;(2)操作的顺序性,问题解决必须包括心理操作过程的序列;(3)认知操作,问题解决的活动必须通过人的认知活动来完成.

对于高中生而言,习题教学是培养问题解决能力的重要途径之一,一个好的习题对于学生而言就是一个科学问题,犹如一个科学问题对于科学家而言就是一道习题一样.学生求解较复杂的物理习题,本质上就是问题解决的过程.尽管物理学中习题解答过程的陈述与心理学中问题解决的一般描述所用叙述语不同,但两者对解决问题过程的陈述还是相近的.结合斯滕伯格的问题解决循环模式,笔者提出如图1所示的高中物理习题解答的“问题解决循环”模式.

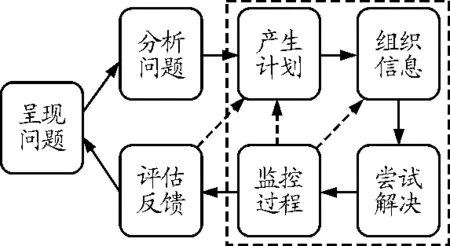
图1　物理习题解答中的“问题解决循环”模式

1基于一题多解的高中物理问题解决循环模式

1.1呈现问题

【题目】(2008年高考全国卷Ⅰ理综第21题)一束由红、蓝两单色光组成的光线从一平行玻璃砖的上表面以入射角θ射入,穿过玻璃砖自下表面射出.已知该玻璃对红光的折射率为1.5,设红光与蓝光穿过玻璃砖所用的时间分别为t1和t2,则在θ从零逐渐增大至90°的过程中

A. t1始终大于t2

B. t1始终小于t2

C. t1先大于后小于t2

D. t1先小于后大于t2

1.2分析问题

分析问题是解决问题的第一步.对问题的分析主要集中在“已知什么”与“要达到什么目的”.引导学生分析问题的教学步骤一般是:教师先示范给学生看如何分析问题,然后和学生一起分析问题,最后让学生独立分析问题.初次接触上题时,师生共同分析可以得到的相关信息如下.

已知:(1)红、蓝光在上表面的入射角均为θ;(2)玻璃对红光的折射率为1.5;(3)红光穿过平行玻璃砖的时间t1;(4)蓝光穿过平行玻璃砖的时间t2.

总目标:θ从零增大至90°的过程中,比较t1和t2的大小关系.

1.3产生计划

习题解答的计划应包括总的目标，如何解决问题以及解决问题需要哪些策略和能力.学生如果在习题解答前有了一个计划,他们解决问题的活动就是理性的.如题中要比较时间,则可以根据逆向推理来制定计划，如图2所示.

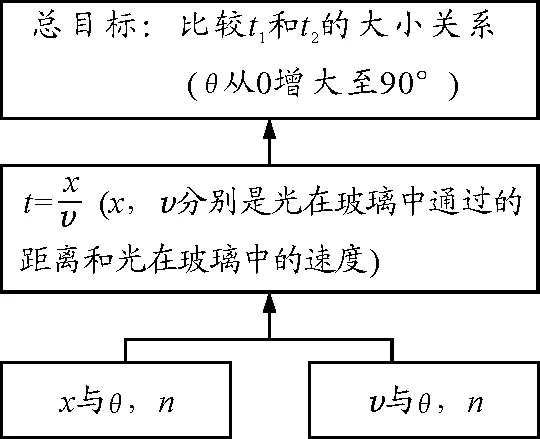
图2　目标分解示意图

1.4组织信息

要想解决一个特定的问题,学生必须具有一定的知识和能力储备,要能回忆已有的信息或获得新的信息,从而缩短目标状态与起始状态之间的距离.如题中分目标的突破,需要一定的知识基础,这可以从已有的知识结构中直接调用.结合图3,可以调用的相关信息如下(说明:红光和蓝光对应的物理量分别用脚标1，2加以区分).

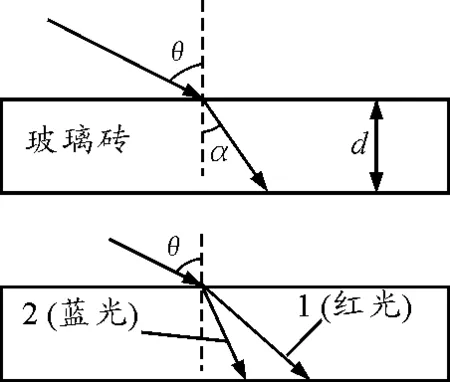
图3　光路图

信息1: n2> n1=1.5;

信息2: α2max<α1max<45°;

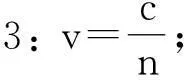
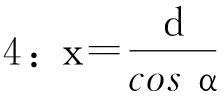
1.5尝试解决

利用各种信息并发挥自己的思维能力,产生一个问题解决的方案,并对物理习题进行尝试性解答.如

令

其中0≤sin2θ≤1,n≥1.5.

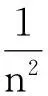
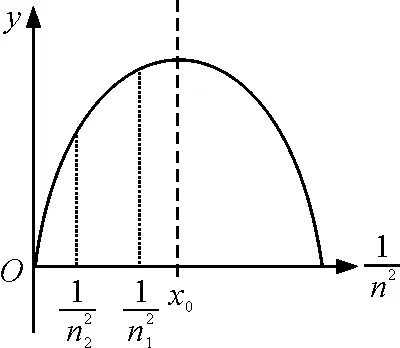
图4　函数y(x)图像

则

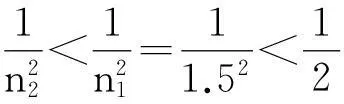
因此y1>y2,从而得到题设条件下始终有t1

点评:此解法凸显极强的数学功底,具有清晰的解题思路,但可能“时不我待”.

1.6监控过程

在习题解答过程中,有效的问题解决者不仅在解决问题后反思,而且更重要的是监控自己解决问题的每一步,以确保最快、最有效地达到解决问题的目标.上述求解过程保留了折射率,显得复杂繁琐,难度较高,肯定不是最佳方案.其实仔细分析会发现

方案1:消去变量α(即上述解法)

方案2:消去变量n

因为

所以α2max<α1max<45°,即在θ从零增大至90°的过程中

2α2<2α1<90°

sin2α2

则t1

点评：方案2能很好地考查运用数学工具解决物理问题的能力,但要求仍较高且物理“味道”较淡!

1.7评估反馈

就像问题解决需要监控一样,也需要对问题解决进行评估.通过评估,新问题才会被识别,已有的知识能力结构才能得到补充和完善.评估反馈可能意味着问题解决的结束,也可能是问题解决的开始.

如在本题的实际教学中,学生提出可以用惠更斯原理(介质中任一波面上的各点,都可以看做发射子波的波源,其后任意时刻,这些子波在波前进方向的包络面就是新的波面)来求解.

如图5所示, ABE为某一时刻的波面,AC为红光在介质中的路径,其所需时间等于光在真空中从B到D的时间(图中AC垂直于CD);AF为蓝光在介质中的路径,所需时间等于光在真空中从E到G的时间(图中AF垂直于FG),且BD和EG相互平行.所以只要比较BD和EG的大小关系,即通过比较D,G的位置关系就可以得到t1和t2的大小关系.

图5　红光、蓝光折射示意图

由图可得

当α=45°时取等号.

由题意可知α蓝<α红<45°,所以图5所示是符合题设条件的,即D在G的左侧(BD < EG),因此t1

点评:利用惠更斯原理分析解决此题,既加深了对已学知识的理解,又促进了学生运用数理方法解决问题的能力,有利于提升学生问题解决的能力.

虽然高中物理习题解答的“问题解决循环”模式包括上述7个步骤,但在实际的物理习题解答过程中,各步骤之间的顺序不是固定的,成功的物理习题解答是上述步骤的灵活使用.

2基于问题解决能力培养的一题多解

让学生掌握问题解决的常规步骤,有利于提高他们问题解决的能力.H.J.Klausmeier(美国威斯康辛大学)提出了问题解决的常规步骤,如图6所示.

图6　 Klausmeier提出的问题解决步骤

对应习题教学的步骤就是:审题—析题—解题—思题.从心理学范畴来说,培养问题解决能力主要从以下几个方面进行.

2.1逻辑推理能力

问题解决需要借助于推理进行,所以推理能力发展水平的高低直接影响一个人问题解决的能力.高中物理教学可以借助一题多解来训练逻辑推理能力.

【例1】设有一架直升飞机以加速度a从地面由静止开始竖直向上起飞,已知飞机在上升过程中每秒的耗油量V0=pa+q(p和q均为常量).若直升飞机欲匀加速上升到某一高度处,且耗油量最小,则其加速度为

解法1:设经过时间t,直升飞机耗油量为V，有

点评:解法1侧重于数学求极值,解法2则利用单位制相关知识进行逻辑推理,回避了复杂的数学运算.

2.2扩大知识面

学生掌握了问题解决的常规步骤后,如果有丰富的知识,对于提高学生问题解决能力有很大的作用.

【例2】如图7所示,一质量为m的物体恰能在一个质量为M,倾角为θ的斜面体上沿斜面匀速下滑.当对物体施加如图所示的恒力时,地面与斜面体之间的摩擦力如何?

图7

分析:物体沿斜面匀速运动,则μ=tanθ.

解法1:先对物体分析,再考虑斜面在水平方向的受力.

解法2:引入“摩擦角”.

令摩擦因数μ等于某一角度α的正切值,即μ=tanα,这个α角称为摩擦角.摩擦角是正压力FN与最大静摩擦力Fm(一般认为等于滑动摩擦力)的合力R与接触面法线间的夹角.

物体原来匀速运动,所以R与重力mg等大反向,摩擦角等于斜面倾角,即α=θ.

当施加外力后,只要物体仍沿斜面下滑,始终有Ff=μFN,即R方向不变,所以物体对斜面作用力竖直向下,斜面与地面间不存在摩擦力.

拓展提升:物体原来沿斜面匀速下滑,当力F作用于物体上时,则地面与斜面间摩擦力为零(物体仍沿斜面下滑).

练习(2010年嘉兴市物理竞赛卷):如图8所示,用绳通过定滑轮牵引物块,使物块在水平面上从图示位置开始沿地面做匀速直线运动,若物块与地面间的动摩擦因数μ<1,滑轮的质量及摩擦不计,则在物块运动过程中,以下判断正确的是

A．绳子拉力与物块重力的合力将保持不变

B．绳子拉力将不断增大

C．地面对物块的摩擦力与地面对物块支持力的合力不断增大

D．物块重力与地面对物块支持力的合力不断减小

图8

点评:“摩擦角”的引入,可以使物块受到的4个力(重力、支持力、摩擦力与绳子拉力)转化为“三力问题”,且一力恒定(重力G),一力方向不变(支持力与摩擦力的合力R),另一力(绳子拉力F)方向改变引起R与F的变化.这就将其纳入已有知识结构(三力问题).

2.3注意掌握好的问题解决策略

好的问题解决策略，是长期问题解决的经验总结，它对于解决特定问题很有效.因此教师要经常教给学生一些好的问题解决策略，同时教师还要鼓励学生自觉地总结自己解决问题时所用的策略.

2.3.1合理选择研究对象

例2(题见前面)的第3种解法如下.

解法3:选择斜面为研究对象,考虑斜面与地面间的摩擦力问题,只要研究物体对斜面的正压力与摩擦力在水平方向上的分力大小关系即可.因为

fx=fcosθ=μFNcosθ=

FNtanθcosθ=FNsinθ=FNx

所以地面对斜面的摩擦力为零.

2.3.2合理选择解题方法

【例3】一条笔直的公路上依次设置3盏交通信号灯L1，L2，L3,其中L2与L1相距80m,L3与L1相距120m.每盏信号灯显示绿色和红色的时间间隔都是20s和40s.L1与L3同时显示绿色,L2则在L1显示红色经历了10s时开始显示绿色,规定车辆通过3盏信号灯经历的时间不得超过150s.若有一辆匀速向前行驶的汽车通过L1的时刻正好是L1刚开始显示绿色的时刻,则此汽车能不停顿地通过3盏信号灯的最大速率______m/s;若一辆匀速向前行驶的自行车通过L1的时刻是L1显示绿色经历了10s的时刻,则此自行车能不停顿地通过3盏信号灯的最小速率是______m/s.

分析:只需在x-t图(如图9所示)上标出绿灯时间,找出符合要求的图线使之穿过L2与L3的绿灯时间区域,其斜率即对应要求的加速度.

图9　3个灯显示绿色的示意图

(1)每盏信号灯显示绿色的时间间隔都是20s,显示红色的时间间隔都是40s;

(2)L1与L3同时显示绿色,L2则在L1显示红色经历了10s时开始显示绿色.

点评:在问题解决过程中,要善于合理选择研究对象与解决问题的方法.

2.4提高思维水平——多角度审视问题

在问题解决的过程中,如何进行有效地思考才能使问题得到较好地解决呢?这就需要一个人不断地提高思维的水平.

【例4】可视为质点的小球从斜面顶端以初速度v0水平抛出,最后仍落在斜面上,求小球在运动过程中与斜面的最远距离.

解法1:推论法(略)

解法2:分解法(考虑小球在垂直斜面方向的运动,略)

解法3:解析法

图10

配方求极值得

点评:在解决问题的过程中,不能老用一种方法去试图解决眼下的问题,而忽略了其他的可能性.学生应灵活机动地进行思维训练,学会从多个角度审视问题.

练习:已知O，A，B，C为同一直线上的4个点,A与B间的距离为l1,B与C间的距离为l2，一物体自O点由静止出发,沿此直线做匀加速运动,依次经过A，B，C 3点,已知物体通过AB段与BC段所用的时间相等.求O与A的距离.(思路:基本公式法;推论法;图像法.)

解法1:打包过渡性未知量aT2.

解法2:纳入初速度v0=0,简化列式.

解法3:利用t2-t1=t3-t2,发挥时间的桥梁作用.

解法4:利用“纸带公式”,涉及相同时间的两段位移问题,会优先调用“纸带公式”.

解法5:利用“比例数据”.初速

度v0=0或末速度vt=0的匀变速运动分段类问题,可考虑利用比例数据解题.

解法6:利用“平均速度公式”,化平均为瞬时.

解法7:图像法.公式法有困难时,总能想起还有图像法.

3结束语

问题解决循环模式下的 “一题多解”,一方面让学生掌握问题解决的常规步骤并利用它分析、解决问题,有利于提高问题解决的能力;另一方面能在实现习题知识技能价值的同时,突显过程与方法、情感态度与价值观的课程目标.当然,不掌握有关的事实、技能和技术,不掌握物理学的基本知识和技能,就什么问题都解决不了,也就谈不上通过一题多解来培养学生的问题解决能力.

同时，高中物理习题的“一题多解”应与“一题多变”、“多题一解”相结合,以使习题发挥更大的功效.

参 考 文 献

1R.J.Sternberg.CognitivePsychology.FortWorth:HarcourtBraceCollegePublishers

2张大均.教育心理学.北京:人民教育出版社,2006

3物理课程教材研究开发中心.普通高中课程标准实验教科书 物理·选修3-4.北京:人民教育出版社,2010.40～42