基于氯盐最不利侵蚀下锈蚀RC框架结构时变地震易损性研究

第一作者郑山锁男，教授，博士生导师，1960年4月生

基于氯盐最不利侵蚀下锈蚀RC框架结构时变地震易损性研究

郑山锁，杨威，秦卿，李磊,邓国专

(西安建筑科技大学土木工程学院，西安710055)

摘要：基于一维Fick第二定律，采用DuraCrete规范中钢筋锈蚀初始时刻的概率预测模型，并基于概率统计的钢筋直径预测模型，计算不同龄期下RC结构中钢筋的锈蚀深度。基于修正斜压场理论并以锈蚀深度为单变量，对不同龄期下受压区锈胀开裂混凝土峰值应力进行计算；根据锈蚀深度对钢筋本构和Mander约束混凝土本构模型中相关参数进行了修正。于地震易损性模型中引入时间参数，建立含时间参数的RC结构地震易损性模型。最后，基于上述材料力学性能退化模型，采用基于力的纤维塑性铰模型，建立三层RC平面框架结构数值模型，并结合本文所提出的时变地震易损性模型，给出了三层平面RC框架0、5、10和15年龄期的易损性曲线和曲面。所提研究方法可用于既有RC框架结构生命周期内的抗震性能及损失预测分析。

关键词：氯离子；RC框架结构；IDA方法；地震易损性分析；多龄期；SeismoStruct

基金项目：国家科技支撑计划(2013BAJ08B03)；国家自然科学基金(50978218，51108376)；教育部高等学校博士学科点专项科研基金(20136120110003)；陕西省科研项目(2012K12-03-01，2011KTCQ03-05，2013JC16)

收稿日期：2014-01-08修改稿收到日期：2014-04-16

中图分类号:TU375

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.006

Abstract:Based on a one-dimensional Fick’s second law and the probability prediction model of initial corrosion time in DuraCrete Code, the remaining reinforcement diameters were calculated by the Statistical formula. Considering the cracking and spalling in the compressed concrete of compression zone caused by reinforcement corrosion, the modified compression-field (MCF) was used to predict the peak value of compressive strength by the function of the single-factor time-dependent remaining reinforcement diameters. Concerning parameters of the material constitutive models of corroded reinforcement and Mander confine concrete were also modified by the remaining reinforcement diameters. At the same time, the time-dependent fragility model was developed for corroding reinforced concrete (RC) frame designed according to the Chinese Code with a merger between a probabilistic model for chloride-induced corrosion and fragility model for undamaged RC frames. Finally, with the forced-based fiber plastic hinge model, the software SeismoStruct was employed to build the numerical model of the three-floor plane frame. Based on the material degradation models presented above, the time-dependent fragility curves and surfaces of three-floor RC frame in four ages(i.e., non-corroded (t=0), 5, 10and 15 years), corresponding to different performance levels, were depicted by the incremental dynamic analysis(IDA) method. This method may be employed to predict service-life and life-cycle cost analysis of RC frame structures

Study on time-dependent seismic fragility analysis of RC frame structures corroded by the most disadvantageous chloride attack

ZHENGShan-suo,YANGWei,QINQing,LILei,DENGGuo-zhuan(School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China)

Key words:chloride; RC frame; IDA method; seismic fragility analysis; multi-age; Seismo Struct

RC结构耐久性损伤领域中，氯离子侵蚀环境下RC结构钢筋锈蚀成为导致结构性能退化的首要因素，目前国内外对于氯离子侵蚀环境下RC结构抗震性能的研究重点主要集中于RC构件锈层次抗震性能的衰减规律，而对于RC整体结构抗震性能的研究还未曾涉及，究其原因主要由于RC整体结构中各构件侵蚀程度呈现空间性和时间性，对于服役RC结构仅能通过现场实测得到结构中各个构件的锈蚀程度，然后在借助于有限元软件建模分析RC整体结构的抗震性能衰减规律。基于以上研究现状，作者提出基于氯盐最不利侵蚀环境下RC整体结构的抗震性能研究，将结构中各构件锈蚀程度按此构件处于理想最不利侵蚀状态下构件的锈蚀程度计算即忽略结构中构件锈蚀程度的空间分布，并考虑时间对结构锈蚀程度的影响，对于考虑耐久性损伤的RC整体结构进行了基于构件层次的结构数值建模方法进行了初步探究。

鉴于此，本文选取RC框架结构，将钢筋时变锈蚀引入结构地震易损性分析中，旨在得到多龄期框架结构的时变地震易损性曲线。结合箍筋与纵筋的锈蚀量相关规律的研究成果，考虑RC结构处于正常使用状态标准下的工作性能，作者认为仅有必要对纵筋锈蚀率低于10%的RC框架结构进行数值建模，因为钢筋锈蚀率低于10%时，锈蚀钢筋的粘结性能降低的并不明显，因此本文在数值建模中并没有考虑锈蚀钢筋的粘结性能劣化。

目前国内外对于锈蚀钢筋混凝土结构的数值模拟方法主要有以下二种：

(1)基于实体单元建模[1]，从材料层面，通过修改材料的本构关系，实现锈蚀钢筋混凝土梁柱的数值建模，定量的分析锈蚀构件的静力及抗震性能随着构件劣化程度的变化规律。

(2)基于截面弯矩-曲率关系的塑性铰模型[2]，通过截面分析软件(Xtract、Semap等)得到RC梁柱塑性铰的模型，接着对其进行简化(两折线、三折线)，采用现有商业有限元软件Sap2000、Capp及Midas等进行Pushover静力非线性分析。

综上所述，本文提出采用可以考虑弯矩-轴力耦合的基于材料的纤维塑性铰模型，对轻微锈蚀RC三层多龄期框架进行了增量动力(IDA)分析，建立结构时变地震易损性曲线。由于氯离子侵蚀及锈蚀模型的不确定性，文中对于龄期的假定、材料强度的折减模型及截面的缩减模型，均选取了概率预测模型，旨在能够更加真实的反应既有RC结构地震易损性的时变特性。

1RC结构使用年份预测

为确定开始锈蚀的时间，扩散模型取为基于一维的fick第二定律[3]，在时刻t深度为x时氯离子的浓度表达式：

(1)

式中：CS为表面的氯离子的浓度，erf(·)为误差函数，D扩散系数，t为从建造开始结构的服役龄期。

1.1钢筋临界锈蚀时间计算理论

DuraCrete[4]考虑测量参数的不确定性、环境条件的不同及模型的不确定性，提出了氯离子作用下钢筋锈蚀开始时间的概率模型，计算公式如下：

Tcorr=

(2)

式中：X1为fick第二定律理想化模型的不确定参数；Ke为环境因子；t0养护时间；Kt计算氯离子扩散系数D0的影响因子；Kc为养护时间的修正系数；dc混凝土保护层厚度；Ccr为氯离子的浓度；Cs氯离子在钢筋的表面的浓度；n为老化因子；Cs表示为W/b的线性函数，计算公式为Cs=ACS(w/b)+εcs，式中ACS、εcs为模型参数，w/b为修正后水灰比；令z=1-Ccr/Cs，则erf-1(z)为误差函数的逆矩阵，可表示如下：

(3)

1.2钢筋锈蚀深度计算理论

由于钢筋锈蚀速度与诸多自身与外部环境均有关系，诸如：混凝土保护层厚度、水灰比、配筋率等设计参数、构件所处结构中的位置及外部环境的变化，且缺乏钢筋锈蚀速度随时间变化情况的现场测量数据，因此本文采用Choe[5]提出的基于概率的钢筋直径预测模型，计算公式如下：

(4)

式中：Tf=Tcorr+dbi{dc/[1.050 8(1-w/c)-1.64]}1/0.71；dbi在t=0时钢筋初始直径；w/c为水灰比；dc为保护层厚度；t为钢筋混凝土结构的使用年份。

上述基于概率的锈蚀钢筋直径预测模型，预测结果为某一环境下锈蚀钢筋剩余直径的平均值，由此所得各种材料参数的退化也为均值。

2材料耐久性衰变规律

2.1受压区混凝土力学性能退化规律

通过减少位于保护层混凝土单元的强度和延性，来考虑受压区混凝土的裂缝和碎裂的影响。Vecchio等[6]提出的模型认为，受压混凝土强度的减少取决于横向平均拉应变的大小，而横向平均拉应变则引起构件的纵向微裂缝，受压区混凝土强度衰减模型计算式：

(5)

ε1=(bf-b0)/b0

(6)

式中：b0为初始状态时截面的宽度(没有出现锈蚀裂缝)；bf为由于锈蚀开裂后梁截面的宽度。梁宽度的增加量可以通过如下式近似估计：

bf-b0=nbarswcr

(7)

式中：nbars为顶层钢筋的数量(受压钢筋)；wcr为对于一个给定的锈蚀程度x的总的裂缝宽度。

与受压区混凝土强度折减规律类似，混凝土抗拉强度计算公式如下：

(8)

Molina 等[7]提出的锈蚀深度x和裂缝宽度wcr之间的就算关系如下式：

(9)

式中：υrs为锈蚀膨胀系数；μicorr为单位周长上的裂缝宽度；对于υrs的取值情况，Molina等取为2。

2.2核心区约束混凝土力学性能退化规律

箍筋直径的锈蚀导致核心区混凝土约束系数的降低，本文采用Mander等[8]混凝土约束本构模型计算约束混凝土强度，混凝土的极限压应变计算公式如下：

(10)

式中：fyh为箍筋的屈服强度，εsyh为箍筋最大拉应力时拉应变，ρv为箍筋的体积配箍率，fcc为约束混凝土的强度。

约束混凝土的强度fcc的计算式如下：

(11)

式中：fc为无约束混凝土的抗压强度；fl′为混凝土的有效侧向约束应力。

2.3锈蚀钢筋力学性能退化规律

对于锈蚀后钢筋的力学性能退化规律按照如下式[9]考虑：

(12)

(13)

(14)

εsuc=e-2.501ηsεsu0

(15)

(16)

式中：Es0为钢筋的弹性模量；ηs为钢筋锈蚀率；fy0,fu0分别为未锈蚀钢筋的屈服强度、极限强度；fyc,fuc分别为锈蚀钢筋的名义屈服强度、名义极限强度；εsy0，εsu0，εsh0分别为未锈蚀钢筋的屈服应变、极限应变和强化应变；εsc，εsuc，εshc分别为锈蚀钢筋的屈服应变、极限应变和强化应变；ηs,cr光圆钢筋取10%，变形钢筋取20%。上述公式的适用条件为ηs<80%。

2.4锈蚀框架梁柱塑性铰长度计算理论

基于构件层次的RC框架整体结构数值建模过程中，考虑钢筋锈蚀及混凝土开裂对框架宏观梁柱单元塑性铰长度的影响，按照公式(17)(18)定义未锈蚀与锈蚀后框架梁柱单元塑性铰区域长度[10]：

lp=0.08Ls+0.022dpfy

(17)

(18)

3锈蚀RC框架时变地震易损性模型

结构风险等于灾害的年发生概率乘以相应的结构年预期损伤，式如下：

Rs=Probability×Damage

(19)

文中仅考虑全寿命周期下结构的风险，鉴于存在两种潜在的危险(钢筋的锈蚀及地震激励)，将式(19)中Probability拆成如下两部分：

Probability=P(corr)×P(seism)

式中：P(corr)和P(seism)分别表示某种锈蚀水平和某一强度地震发生的年超越概率，两者相互独立。因此，同时考虑结构锈蚀和地震危害下结构的风险计算式如下：

Rs=P(corr)×P(seism)×Damage

(20)

为对近海既有RC框架结构进行损失评估，须同时考虑环境引起的RC框架结构中钢筋锈蚀与遭遇地震作用的影响，为此提出如下考虑钢筋锈蚀的RC框架地震易损性模型。

3.1概率地震需求模型

(21)

式中：α(t)、β(t)为结构某一龄期的回归参数，IM为地震动强度指标，鉴于多龄期结构的第一阵型周期随龄期的变化规律不确定，因此本文中选用PGA作为地震动强度指标。对上式两边取对数得：

(22)

式中：a(t)、b(t)均为常数，a(t)=lnα(t)、b(t)=β(t)，可通过结构的增量动力分析数据结果统计回归得到。对数正态分布的标准差σ为：

(23)

式中：di(t)为t时刻第i个地震动的需求值。

根据式(21)~(23)，结构概率地震需求计算公式为：

Pd(t)=P[D(t)≥d(t)|IM]=

(24)

此概率地震需求模型，未考虑结构几何模型与材料的不确定性。

3.2概率地震能力分析

结构概率地震抗震能力分析(seismic capacity)就是确定针对某个特定破坏极限状态或性能水平的界限值。由于文中未考虑结构几何模型与材料的不确定性，因此把结构的抗震能力当作是确定性的，不考虑结构能力的不确定性。选取最大层间位移角θmax作为结构损伤指标，θmax取1%、2%和4%作为三种损伤状态对应的RC平面框架结构极限状态指标，见表1。

表1　FEMA 356 [12]定义的不同性态水平的层间位移角限值

3.3结构地震易损性分析

结构的地震易损性是指结构在不同水平的地震作用下，发生不同程度破坏的可能性或者说是结构达到某个极限状态(性能水平)的概率，如下式所示：

Fragility(t)=P[D(t)≥C(t)|IM]

(25)

假定t时刻结构的地震需求D(t)与地震能力C(t)均服从对数正态分布[13]，结构特定阶段的失效概率Pf表示为：

Pf(t)=P[D(t)≥C(t)|IM]=

(26)

将式(21)代入式(26)可以改写为如下形式：

Pf(t)=P[D(t)≥C(t)|IM]=

(27)

(28)

式中：m(t)和ζ(t)分别为全寿命周期内t时刻的地震易损性函数的中位值(单位g)和结构地震易损性函数的对数标准差，DS为损伤状态。

3.4地震易损性曲面

根据式(28)绘制各龄期的地震易损性曲线，为对任意龄期结构的失效概率进行预测，将0、5、10与15年结构易损性函数中的均值m(t)和方差ζ(t)进行多项式拟合，建立以地震动强度指标PGA，结构龄期及失效概率作为坐标的易损性曲面，具体拟合与易损性曲面绘制过程详见算例。

4算例

按照我国规范采用结构设计通用软件PKPM(2010版本)，设计一三层框架结构。柱网采用6 m×6 m，平面布置如下图1所示。层高均为3.3 m。抗震设防烈度为8度，设计基本地震加速度为0.2 g，地震分组为第一组，场地类别为Ⅱ类，为二级框架。

框架顶层恒荷载、活荷载分别取9.0 kN/m2、0.5 kN /m2；标准层恒荷载、活荷载分别取为8 kN /m2、2 kN /m2。混凝土等级均为C40。钢筋材料使用情况为：梁柱纵筋均采用HRB335级，箍筋采用HPB235；楼板厚度均采用120 mm，纵横向板筋均采用HPB235。

4.1结构设计资料

设计平面和立面规则RC空间框架结构，选取其主轴方向一榀平面框架(见图1)进行IDA分析。楼层重量按照(l.0×恒载十0.5×活载)折算，梁上均布荷载和节点集中荷载参照PKPM程序导出结果取值，框架受力简图如图2，框架梁、柱截面尺寸、各楼层梁端、柱端配筋面积详见表2。

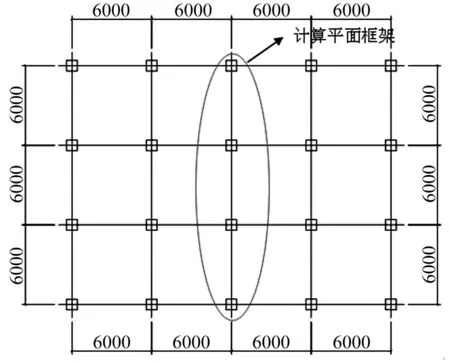
图1　三层框架结构平面布置图 Fig.1 Layout plan of three-floor frame structure

图2　三层框架受力简图 Fig.2 Load diagram of three-floor frame structure

框架名称层号梁尺寸(mm×mm)梁端配筋上下柱尺寸(mm×mm)柱配筋(单侧)边柱中柱1218+4Φ202Φ18+2Φ20三层2300×500(C40)2Φ16+4Φ182Φ18+2Φ20400×400(C40)218+2Φ221Φ16+2Φ1832Φ16+4Φ162Φ18+2Φ20

4.2材料本构

混凝土采用Mander约束混凝土本构关系，钢筋采用Menegotto-Pinto钢筋本构模型。三层平面RC框架结构梁柱塑性铰长度均取为0.8倍截面高度。

4.3龄期假定

根据第2小节相关内容可知，只要确定钢筋的锈蚀深度，即可根据式(5)~(16)，计算以下折减系数：

(1)纵筋与箍筋截面的折减系数，及由此导致的核心区约束混凝土约束系数的降低；

(2)钢筋极限变形与混凝土极限应变的折减系数；

(3)受压区开裂混凝土强度的折减系数。

本文假定RC结构所处环境参数见表3，RC框架梁柱构件保护层厚度取为20 mm。

表3　环境参数取值

根据表2和3，参考DuraCrete规范[4]确定公式中相关参数的取值，根据式(2)计算箍筋、纵筋表面开始锈蚀临界时间Tcorr分别为0.034年、0.098年，基于式(4)计算钢筋剩余直径。由第2小节可知，分析中采用式(9)对锈蚀裂缝宽度Wcr进行预测，并通过式(5)计算受压区混凝土强度折减系数，预测结果见表4。

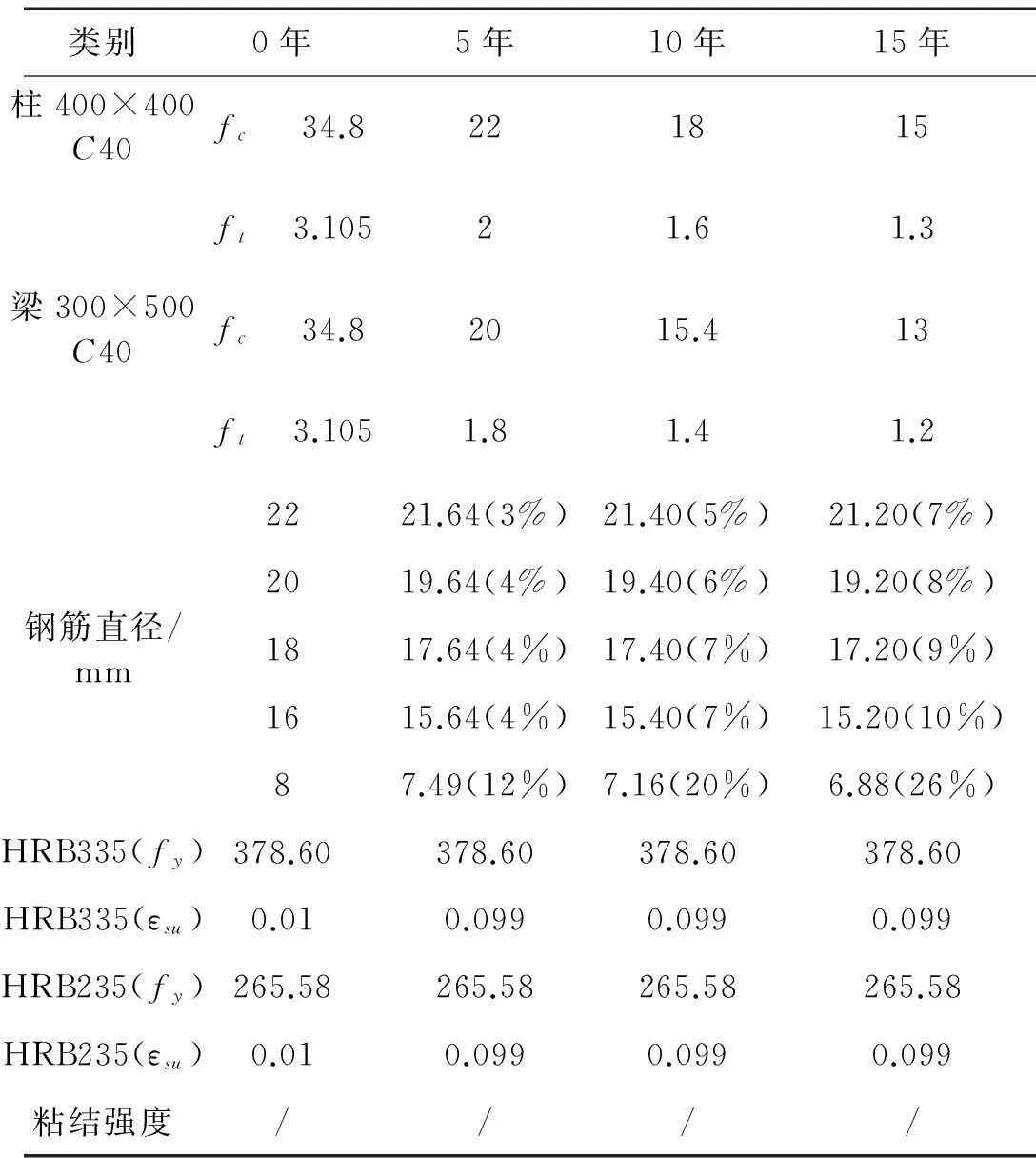
表4　四种龄期下的材料性能

注：括号内为相应的质量损失，钢筋直径单位(mm)，混凝土及钢筋强度单位(MPa)

为便于数值建模分析，经简化(忽略钢筋直径不同的影响)本文对龄期为5、10和15年的钢筋截面面积分别进行4%、7%和9%的缩减；保护层混凝土强度折减系数按表4取值。Capozucca等[14]通过理论分析和试验验证，得出锈蚀RC梁受压区混凝土峰值应力的锈胀开裂损伤系数η取值为0.4~0.67，同表4中锈胀开裂混凝土强度折减系数相吻合。η的计算式为：

(29)

对于纵向受力钢筋(HRB335)，因为锈蚀率均在10%以下[15]，因此可以不考虑钢筋的屈服强度和极限应变的变化并忽略锈蚀钢筋粘结强度的退化；对于截面削弱较多的箍筋(≥12%)，仅考虑箍筋截面减小造成的核心区混凝土约束系数的降低。为此，对于5、10和15年的箍筋剩余直径分别取为7.49mm、7.16mm和6.88mm，受压区开裂混凝土极限压应变按照式(10)计算，核心区约束系数按照Mander公式计算，见式(11)。AbdelsamieElmenshawi(2012)等[16]认为塑性铰长度与构件剪跨比、纵向受拉钢筋直径和屈服强度、箍筋配箍率和屈服强度和截面极限抗剪承载力有关；由于截面的极限抗剪承载力和配箍率同时减小，因此建模中忽略虑塑性铰长度随龄期的变化，采用式(17)计算。

4.4RC平面框架的IDA分析

建立数值模型如图3所示，所选取的11条地震动记录见表5。

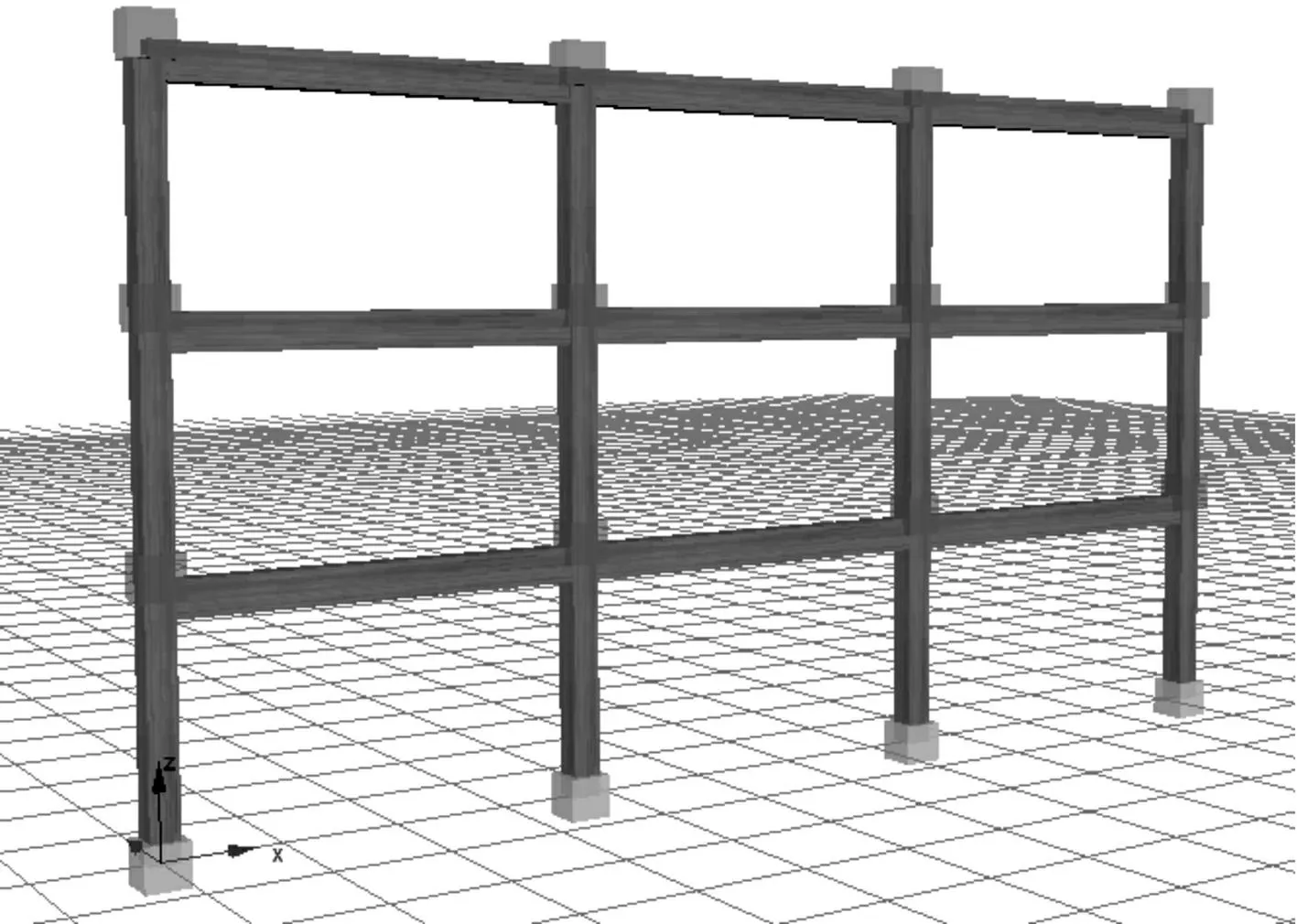
图3　平面框架数值模型 Fig.3 Numerical model of plane frame

根据第3小节的时变地震易损性模型，对不同龄期RC框架结构体系进行IDA分析。根据公式(28)得到，0、5、10及15年RC框架结构地震易损性函数的中位数及方差见表6；对应于IO、LS及CP状态下4个龄期的易损性曲线见图4；不同PGA下(对应于小震、中震、大震及特大震)，不同龄期RC框架结构各性能极限的超越概率见表7。

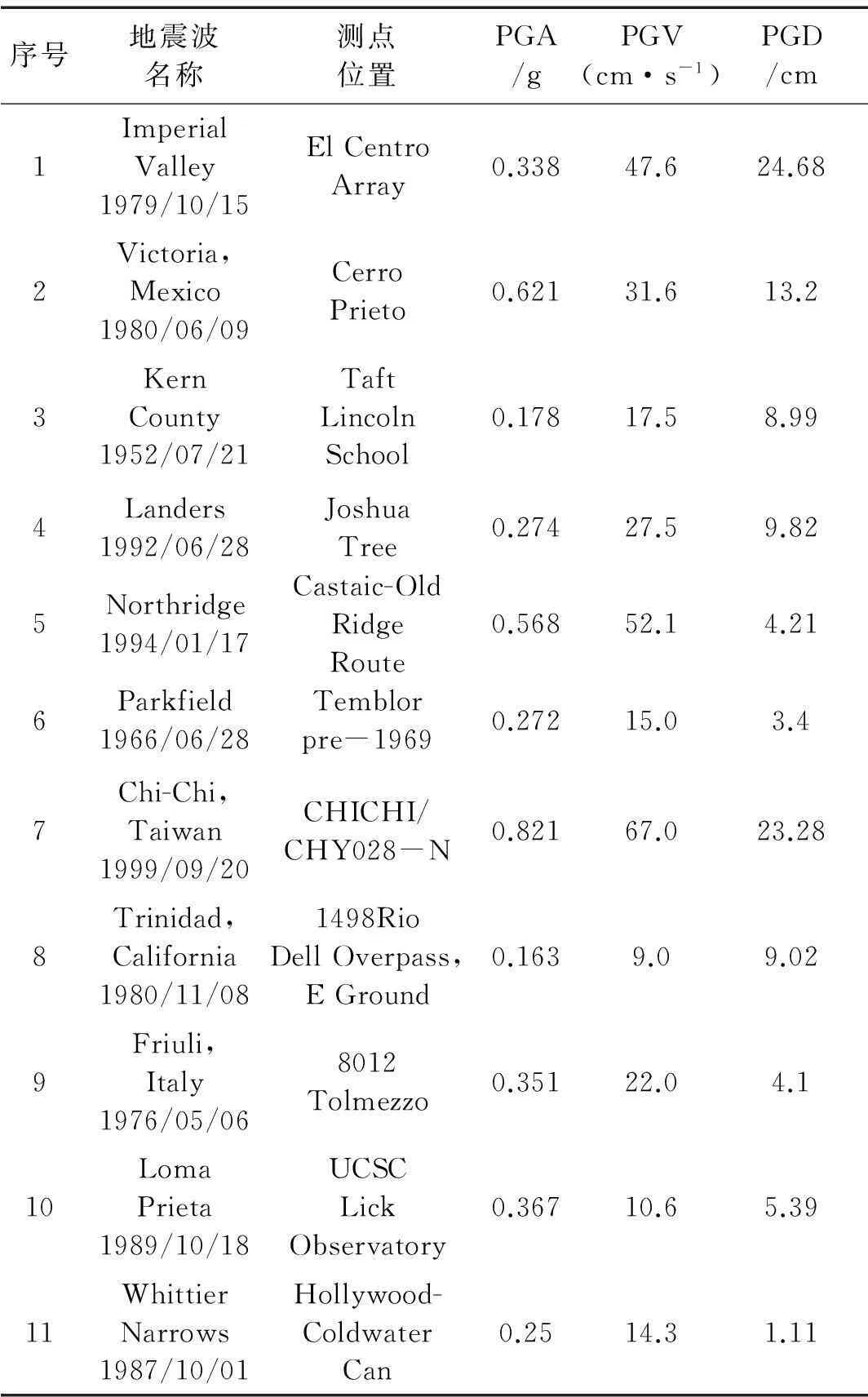
表5　地震动记录

图4　三层RC框架各极限状态的时变易损性曲线 Fig.4 Time-dependent fragility cures of three-floor frame at each limit state

时间(年)性能水平IOLSCPm(t)ζ(t)m(t)ζ(t)m(t)ζ(t)00.2250.8940.5500.8941.3450.89450.2060.8670.4940.8671.1830.867100.1940.8070.4410.8071.0030.807150.1760.7690.3870.7690.8530.769

从图4和表7可知，相同状态下结构的失效概率随着龄期的增大而增大，比如PGA为0.2g时，0年三层RC结构超越IO状态的超越概率为44.84%、超越LS状态的为12.91%，超越CP状态的为1.34%；5年三层RC结构超越IO状态的超越概率为48.6%、超越LS状态的为14.92%，超越CP状态的为2.05%；10年三层RC结构超越IO状态的超越概率为51.71%、超越LS状态的为16.45%，超越CP状态的为3%；15年三层RC结构超越IO状态的超越概率为56.05%、超越LS状态的为21.94%，超越CP状态的为5.6%，因此CP状态下结构的超越概率对龄期最为敏感，LS次之，IO最小。

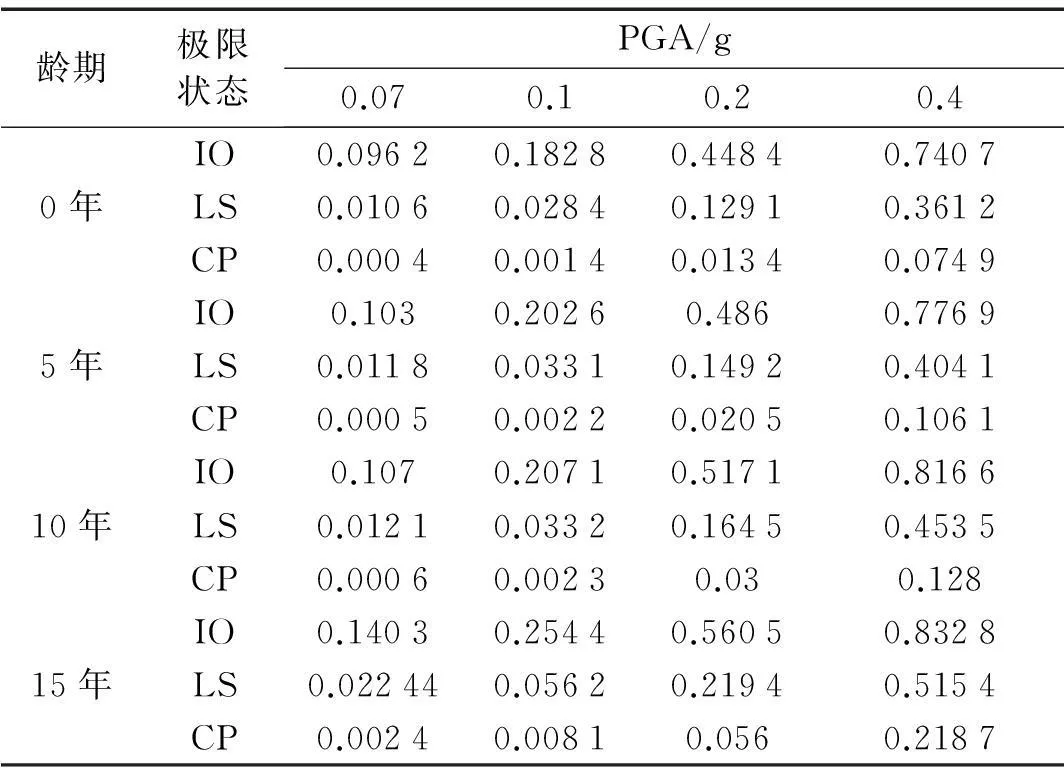
表7　不同PGA下各极限状态(IO、LS和CP)的超越概率

为将离散的时间点变成连续的时间区间，根据Enright等[17]提出的桥梁抗力随时间退化符合二次多项式关系，此处也认为RC框架抗力随时间的退化关系符合二次多项式拟合关系即：

Parameter(t)=at2+bt+c

(30)

将m(t)、ζ(t)按照以上二项式进行拟合，拟合曲线如图5和6所示，参数a、b和c的取值见表8所示。将拟合后所得系数代入式(28)，得到连续化的结构地震易损性曲线计算公式：

P[DS|PGA]=

(31)

根据式(31)和表8，以PGA、超越概率P及时间t建立三维坐标系，得到0到15年三层RC结构IO、LS及CP状态下的空间易损性曲面，如图7所示。

图5　m(t)二项式拟合曲线 Fig.5 Binomial fitting curve of m(t)

图6　ζ(t)二项式拟合曲线 Fig.6 Binomial fitting curve of ζ(t)

图7　三种状态下RC框架时变地震易损性曲面 Fig.7 Time-dependent fragility surface at each limit state (IO、LS and CP)

表8　中位数和方差的二次拟和值

5结论

(1)基于钢筋锈蚀深度概率预测模型和修正修压场理论，以锈蚀箍筋、纵筋、受压区锈胀开裂混凝土及核心区约束混凝土为对象，综合各既有材料退化模型，预测了各龄期下材料的退化后力学性能，与现有单一缩减纵筋直径的数值建模方法相比，考虑钢筋锈胀退化机理更加准确，多龄期RC结构数值建模方法更加合理。

(2)将时间参数引入经典地震易损性模型中，推导了结构地震时变易损性模型的计算公式；

(3)选取合适的单元，实现了一3层平面框架的数值建模。基于时变易损性模型，通过二项式拟合将离散的易损性曲线连续化，给出0~15年区间内任意时刻结构的失效概率，在三维坐标轴上绘制出了相应的易损性曲面，为既有RC结构的直接经济损失及风险实时评估，提供了研究思路。

(4)结构构件锈蚀的空间分布具有复杂性与离散性，本文对结构中的所有构件采用的都是最不利锈蚀状态，其实是在数值建模上进行了简化，仅能得到整体结构处于最不利侵蚀作用下的易损性变化规律。因此今后对于考虑耐久性损伤的整体结构的地震易损性研究，要考虑构件锈蚀空间分布的离散性、结构抗震性能的随机性，获得更为精确的结构

参考文献

[1]Hanjari K Z, Kettil P, Lundgren K. Analysis of mechanical behavior of corroded reinforced concrete structures[J]. ACI Structural Journal, 2011, 108(5): 523-541.

[2]Yalciner H, Sensoy S, Eren O. Time-dependent seismic performance assessment of a single-degree-of-freedom frame subject to corrosion[J]. Engineering Failure Analysis, 2012, 19: 109-122.

[3]Tuutti K. Corrosion of steel in concrete swedish[D]. Stockholm:Cement and Concrete Research Institute; 1982.

[4]DuraCrete. Statistical quantification of the variables in the limit state functions[M]. The European Union Brite EuRam 3 contract BRPR-CT95-0132 Project BE95-1347 Report no BE95-1347/R7 May 2000.

[5]Choe D E, Gardoni P, Rosowsky D, et al. Probabilistic capacity models and seismic fragility estimates for RC columns subject to corrosion [J]. Reliability Engineering and System Safety 2007; 93:383-393.

[6]Vecchio F J, Collins M P. The modified compression-field theory for reinforced concrete elements subjected to shear[J]. ACI Journal, 1986, 83(22): 219-231.

[7]Molina F J, Alonso C, Andrade C. Cover cracking as a function of rebar corrosion: Part 2-Numerical model [J]. Materials and Structures, 1993, 26(9): 532-548.

[8]Mander J B, Priestley M J N, Park R. Theoretical stress-strain model for confined concrete[J]. Journal Structural Engineering, ASCE, 1988,114(8):1804-1826.

[9]张伟平, 商登峰, 顾祥林. 锈蚀钢筋应力-应变关系研究析[J]. 同济大学学报(自然科学版), 2006, 34(5): 586-592.

ZHANG Wei-ping, SHANG Deng-feng, GU Xiang-lin. Stress-strain relationship of corroded steel bars [J]. Journal of Tongji University(Natural Science), 2006, 34(5): 586-592．

[10]Paulay T, Priestley M J N. Seismic design of reinforced concrete and masonry buildings [M].New York: Wiley Interscience, 1992.

[11]Cornell C A，Jalayer F， Hamburger R O，et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering ASCE，2002，128(4)：526-533.

[12]FEMA356. Prestandard and commentary for the seismic rehabilitation of buildings, Prepared by the American Society of Civil Engineers for the Federal Emergency Management Agency, Washington, D.C. Publ. No. 356.

[13]Sucuoglu H, Yucemen S，Gezer A，et al. Statistical evaluation of the damage potential of earthquake ground motions [J]. Structural Safety，1999，20(4): 357-378.

[14]Capozucca R, Cerri M N. Influence of reinforcement corrosion-in the compressive zone—on the behaviour of RC beams [J]. Engineering Structures, 2003, 25(3): 1575-1583.

[15]Lundgren K, Kettil P, Hanjari K Z, e tal. Analytical model for the bond-slip behaviour of corroded ribbed reinforcement [J]. Structure and Infrastructure Engineering, 2012,8: 157-169.

[16]Elmenshawi A, Brown T,El-Metwally S. Plastic hinge length considering shear reversal in reinforced concrete elements [J]. Journal of Earthquake Engineering, 2012, 16(2): 188-210.

[17]Enright M P, Frangopol D M.Condition prediction of deteriorating concrete bridges using Bayesian updating[J]. Journal of Structural Engineering ASCE, 1999, 125(10):1118-1125.