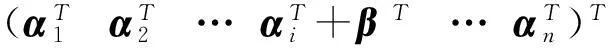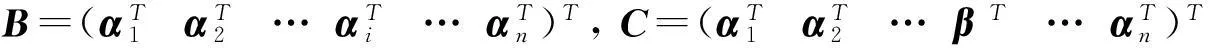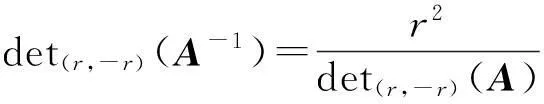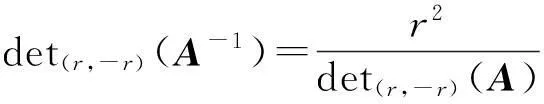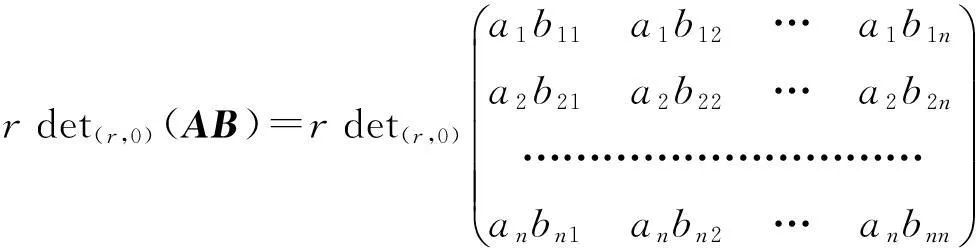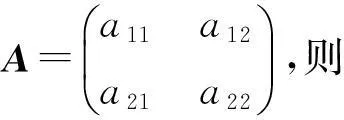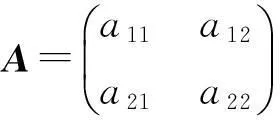由平面方向决定的新型行列式

由平面方向决定的新型行列式

侯汝臣,朱用文,王燕

(烟台大学数学与信息科学学院, 山东烟台264005)

[摘要]设F是一个域.任给F中的一对元素(k1,k2)，给出了(k1,k2)-型行列式的定义.我们指出通常的行列式恰是(1,-1)-型.研究了这些(k1,k2)-行列式的性质，指出和通常行列式的相同和不同之处.刻画了一些特殊的(r,-r)-型, (r,0)-型和(r,r)-型行列式的性质.

[关键词]方阵； 行列式； (k1,k2)-型行列式

[收稿日期]2014-11-20；[修改日期] 2014-12-17

[基金项目]国家自然科学基金(11371307)；烟台大学教学改革研究项目(2012C091, 2014C047)

[中图分类号]O151.22[文献标识码]C

1引言

在线性代数中，方阵A所对应的行列式|A|是一个非常重要的常数.自从莱布尼茨1683年在有记载论文中首次提到行列式到现在，行列式在理论和应用上都取得了丰富成果，参考[1],[2],[3]等.丰富和完善行列式理论的一个重要方向是对行列式理论进行推广性研究.例如，超多项式理论，拟多项式理论，量子多项式理论等等，参考[4],[5],[6]等.本文定义了一种新型行列式,发现这种行列式是通常行列式的一种自然且新颖的推广.对这种新型行列式的性质进行了深刻研究，相当于对通常行列式的性质从一个新的角度进行了全新理解.这样，在教学工作中，我们会引领学生以发散型思维考虑问题，加深对行列式的理解.

若1,2,…,n是n个紧邻自然数，则1,2,…,n按大小关系有自然的序.设i1,i2,…,in是1,2,…,n的 一个排列，则可以定义i1,i2,…,in的逆序数τ(i1,i2,…,in).

设F是一个域，A=(aij)n×n是定义在F上的一个方阵,A所对应的行列式定义为

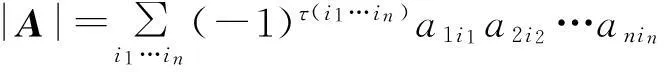
注意到n阶行列式是n!项的和, 每一项与1,2,…,n的一个排列对应，确切的说，同时与排列和排列的逆序数对应.受这种观察的启发，作为通常行列式概念的推广，在本文中给出(k1,k2)-型行列式的定义，其中k1,k2∈F.用P(n)表示1,2,…,n的所有排列组成的集合.

定义1.1设k1,k2∈F, 在P(n)上定义一个映射φ(k1,k2)如下：设σ∈P(n),定义

定义1.2设A=(aij)n×n是域F上的一个方阵,k1,k2∈F,定义

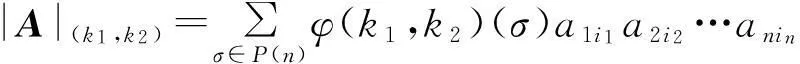
其中σ=i1i2…in.

称|A|(k1,k2) 为A所对应的(k1,k2)-型行列式.也用det(k1,k2) (A)表示A所对应的(k1,k2)-型行列式.注意到det(1,-1)(A)恰好是|A|.所以以上定义的(k1,k2)-型行列式确实是通常行列式的一种推广.根据定义注意到det(0,0)(A)=0.本文将刻画一般(k1,k2)-型行列式和通过赋予k1,k2具体的值得到的一些特殊(k1,k2)-型行列式的性质.如果没有特别指出，规定所有的矩阵都定义在数域F上.

2(k1,k2)-型行列式的性质

设π∈P(n), 规定π所代表的1,2,…,n的排列为π(1)π(2)…π(n).首先注意到, 给定 A=(aij)n×n,k1,k2∈F,有

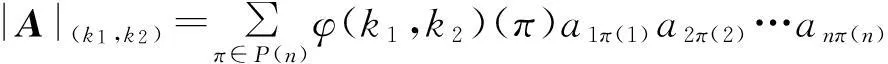
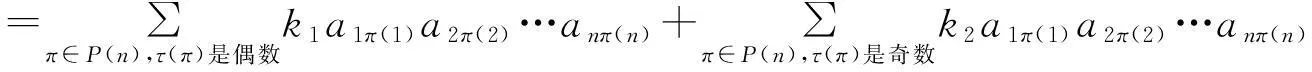
定理2.1如果A是一个n阶方阵,k1,k2∈F,并且k1≠0, 那么

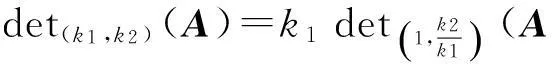
相似的, 如果k2≠0,那么

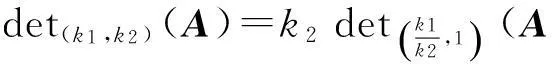
证如果k1≠0, 那么

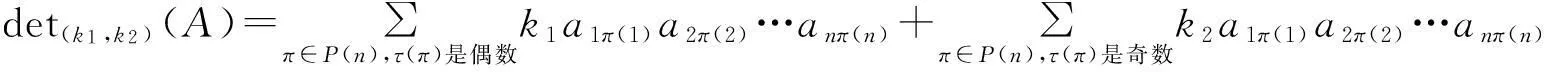
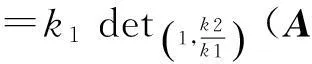
k2≠0情况相似可证. 定理证毕.

如果k1∶k2=k3∶k4，由定理2.1，作为从所有n阶方阵构成的集合到数域F的算子,会有det(k1,k2) 和det(k3,k4) 成固定的比例，所以称(k1,k2)-型行列式为由平面方向决定的行列式.

命题2.2如果A是一个n阶方阵,k1,k2,k3,k4∈F那么

det(k1+k2,k3+k4) (A)=det(k1,k3) (A)+det(k2,k4) (A).

证因为

=det(k1,k3) (A)+det(k2,k4) (A),

所以命题得证.

定理2.3如果A是一个n阶方阵,AT是A的转置矩阵,k1,k2∈F,那么

det(k1,k2) (A)=det(k1,k2) (AT).

证如果能证明det(k1,k2) (AT)中的任意加法项存在于det(k1,k2) (A)中, 那么因为(AT)T=A ，所以det(k1,k2) (A)中的任意加法项也位于det(k1,k2) (AT) 中,因此det(k1,k2) (A)和det(k1,k2) (AT)有相同的加法项，这样就证明了结论. 根据(k1,k2)-型行列式的定义，这是容易证明的.例如, 假设τ(π)是偶数,k1a′1π(1)a′2π(2)…a′nπ(n)是det(k1,k2) (AT)中的一个加法项,在P(n)中存在σ使得

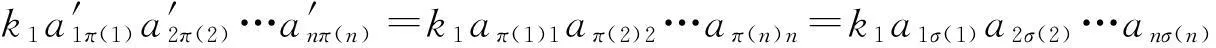
容易证明τ(σ)也是偶数, 因此det(k1,k2) (A)中有这个加法项.证毕.

根据定理2.3知道和方阵A的行相关的det(k1,k2) (A)的性质也对A的列成立.所以为了简便起见，我们只阐述和A的行相关的det(k1,k2) (A)的性质，而对于A的列，det(k1,k2) (A)有完全相同的性质.

和行列式相似，关心在给A一个行变换的情况下，(k1,k2)-型行列式det(k1,k2) (A)的改变.下面的一系列有趣结论对此进行了刻画.

定理2.4如果P是一个n阶行交换基本矩阵, 即P由单位矩阵交换两行得到，A是一个n阶方阵,k1,k2∈F, 那么det(k1,k2) (PA)=det(k2,k1) (A).

证设 1≤u

det(k1,k2) (B)

其中对π进行一次对换可得σ.证毕.

和行列式的行交换性质进行比较, 定理 2.4揭示了更多信息, 更接近本质.

推论2.5如果方阵A有两行相等,k1,k2∈F那么

det(k1,k2) (A)=det(k2,k1) (A) .

证因为A有相同的两行，交换这两行我们还会得到A. 根据定理2.4易证.

设A是一个有两行相等的方阵, 根据推论2.5

|A|=det(1,-1)(A)=det(-1,1)(A)，

而根据定理2.1有

det(-1,1)(A)=-det(1,-1)(A)=-|A|，

所以推出|A|=0.这恰好是众所周知的结论.

det(k1,k2) (A)=det(k1,k2) (B)+det(k1,k2) (C),

det(k1,k2) (A)

=det(k1,k2) (B)+det(k1,k2) (C).

命题2.7如果A是一个n阶方阵， 把A的某行乘以常数r得到方阵B,k1,k2∈F, 那么

det(k1,k2) (B)=rdet(k1,k2) (A).

证设矩阵A=(aij)n×n的u行乘以常数r，其它行保持不变，得到矩阵B=(bij)n×n.则对于i≠u， 有bij=aij,而buj=rauj. 因此

det(k1,k2) (B)

=rdet(k1,k2) (A).

用定义易证下面结论.

命题2.8设A=(aij)n×n是一个n阶上三角方阵,则对k1,k2∈F，有

det(k1,k2) (A)=k1a11a22…ann.

对下三角方阵有相同结论.

3一些特殊的(k1,k2)-型行列式

设k1,k2∈F,根据命题2.2有

det(k1,k2) (A)=det(k1,-k1+k2+k1) (A)=det(k1,-k1) (A)+det(0,k1+k2) (A)，

因此要计算det(k1,k2) (A)只需计算det(k1,-k1) (A)和det(0,k1+k2) (A).所以研究 (r,-r)-型和(0,r)-型行列式很有价值，r∈F.首先，考察(r,-r)-型行列式.

（5）实验课教学组织。每个实验包含预习实验、实验操作、实验结果及处理、实验报告4个环节。其中，实验前预习实验指导，有些实验可以采用PBL、TBL等教学模式让学生完成一定的综合性实验任务；实验过程中，根据实验方案的操作步骤，要求学生认真进行实验，记录实验过程和现象；实验结束后根据要求写出实验报告，有利于学生对实验内容的加深理解。同时，通过实验培养学生严肃、认真、实事求是的科学态度和严谨细致、整洁的良好实验习惯。

命题3.1设A,B是n阶方阵,a,b∈F,则

det(ab,-ab)(AB)=det(a,-a)(A)det(b,-b)(B).

证根据定理2.1有

det(ab,-ab)(AB)=abdet(1,-1)(AB),

det(a,-a)(A)=adet(1,-1)(A) ,det(b,-b)(B)=bdet(1,-1)(B),

又因为

det(1,-1)(AB)=det(1,-1)(A)det(1,-1)(B),

这样就证明了结论.

推论3.2设A,B是n阶方阵,r∈F, 则

rdet(r,-r)(AB)=det(r,-r)(A)det(r,-r)(B) .

证因为rdet(r,-r)(AB)=det(r2,-r2) (AB)，所以根据命题3.1得证.

命题3.3设A是n阶方阵,r∈F,r≠0, 则A可逆当且仅当det(r,-r)(A)≠0.

证因为

det(r,-r)(A)=rdet(1,-1)(A)，r≠0,

所以det(r,-r)(A)≠0当且仅当 det(1,-1)(A)≠0, 而 det(1,-1)(A)≠0当且仅当A可逆.

推论3.4设A是一个n阶可逆方阵,r∈F，r≠0，则

证首先注意到, 根据 (k1,k2)-型行列式的定义det(r,-r)(In)=r. 然后根据推论3.2

rdet(r,-r)(AA-1)=det(r,-r)(A)det(r,-r)(A-1)，

即

rdet(r,-r)(In)=r2=det(r,-r)(A)det(r,-r)(A-1)，

根据命题3.3有 det(r,-r)(A)≠0, 所以

命题3.5设A是一个n方阵, A做一次换行或者换列得矩阵B,r∈F, 那么

det(r,-r)(B)=-det(r,-r)(A).

证根据定理2.4有det(r,-r)(B)=det(-r,r)(A)，又根据定理2.1,有

det(-r,r)(A)=-det(r,-r)(A)，

所以命题得证.

推论3.6如果n阶方阵A的两行相等,r∈F, 那么 det(r,-r)(A)=0.

证这是命题3.5的直接推论.

命题3.7设A是一个n阶方阵，i≠j，r∈F，把A的第j行的若干倍加到它的第i行，其它行保持不变得到矩阵B,那么

det(r,-r)(B)=det(r,-r)(A).

证根据命题 2.6 知存在方阵C使得

det(r,-r)(B)=det(r,-r)(A)+det(r,-r)(C)，

其中C的i,j两行相等, 又根据推论3.6,有det(r,-r)(C)=0. 这就证明了命题.

其次, 考察(r,0)-型行列式.

命题3.8设A 是一个n阶对角方阵, B是一个n阶方阵,r∈F, 则

rdet(r,0)(AB)=det(r,0)(A)det(r,0)(B).

证设A是依次以a1,a2,…,an作为对角元素的n阶对角方阵， B=(bij)n×n， 那么

=det(r,0)(A)det(r,0)(B).

最后,考察(r,r)-型行列式. 根据定理 2.4， 容易证明

命题3.9设A是一个n阶方阵,A经过一系列的换行或换列得到方阵B,r∈F,那么

det(r,r)(A)=det(r,r)(B).

4(k1,k2)-型行列式的一点应用

平面上一点(1,-1)决定的(1,-1)-型行列式恰好就是行列式.行列式在线性代数，微分几何等领域有广泛且深刻的应用.如果k≠0,如文章第三部分所示，平面上点(k,-k)所对应的(k,-k)-型行列式和行列式有着几乎完全相同的性质，所以(k,-k)-型行列式在线性代数，微分几何等领域也会有相似的应用.

det(k1,k2) (A)=k1a11a22+k2a12a21.

容易看出det(k1,k2) (A)的绝对值代表一个以向量(k1a11,a21)T和(-k2a12,a22)T作为两条边的平行四边形的面积.

a11a12×a21a22=(a11×10+a12)×(a21×10+a22)

=(a11+a21)×100+(a11×a22+a12×a21)×10+a12×a22.

此处交叉项10的系数恰好是det(1,1)(A).

[参考文献]

[1]Lay C, David. Linear algebra and its applications [M]. 3rd ed. Boston: Addison Wesley, 2005.

[2]Jacobs D P V, Trevisan.The determinant of a tree′s neighborhood matrix[J]. Linear Algebra and its Applications, 1997, 256(15):235-249.

[3]Formanek E and Sibley D. The group determinant determines the group[J]. Proceedings of the American Mathematical Society,1991,112(3): 649-656.

[4]Glynn, David G. The modular counterparts of Cayley′s hyperdeterminants[J]. Bull. Australian Mathematical Society, 1998, 57: 479-492.

[5]Gelfand I, Gelfand S, Retakh V, Wilson R L. Quasideterminants[J]. Adv. Math., 2005, 193(1):56-141.

[6]Hayqashi T. Quantum groups and quantum determinants[J]. Journal of Algebra, 1992,152:146-165.

New Type Determinants Determined by Directions in a Plane

HOURu-chen,ZHUYong-wen,WANGYan

(School of Mathematics and Information Science, Yantai University，Yantai Shandong 264005, China)

Abstract:Let F be a field, k1,k2∈F. We give a definition of (k1,k2)-determinants, and point out that normal determinants are of (1,-1)-type. We study properties of (k1,k2)-determinants, compare (k1,k2)-determinants with normal determinants, find out differences and similarities between them. We also describe properties of special (k1,k2)-determinants such as (r,-r)-tpye, (r,0)-type, and (r,r)-type.

Key words: square matrix; determinant; (k1,k2)-determinant