环F2+uF2+…+ukF2上的Type Ⅱ码

环F2+uF2+…+ukF2上的Type Ⅱ码

王永1,2

(1.合肥工业大学数学学院，合肥230009；2.安徽省肥西中学，合肥231200)

[摘要]给出一种构造环F2+uF2+…+ukF2上任意偶数长度的自正交和自对偶码的方法.定义了环F2+uF2+…+ukF2的每个元素的Euclidean重量并且证明了环F2+uF2+…+ukF2上的自对偶码是Euclidean重量为2k+2倍数的Type Ⅱ码.

[关键词]自对偶码； 自正交码； Euclidean重量； Type Ⅱ码

[收稿日期]2014-03-11

[中图分类号]O157.4[文献标识码]C

1引言

多项式剩余类环的结构介于有限域和环之间，因其具有良好的性质，其上的纠错码理论研究也引起了编码学者的关注.其上的码被广泛加以研究[1-5].自对偶码是一类非常重要的线性码，许多最优的线性码都来源于自对偶码.此外，自对偶码具有丰富的数学性质，可用于区组设计、模格构造等.因此自对偶码备受关注.近年来，多项式剩余类环上的自对偶码的研究也颇多.Bonnecaze等人在[6]中研究环F2+uF2上的循环码及其对偶码.

自对偶码中有一类码称为Type II码，其具有很好的性质，因此更是人们研究的重点.文献[7]研究了环F2+uF2上的Type II 码，随后Ling等人[8]将其推广到环F4+uF4.Bestumiya等人[9]将其推广到更为一般的环F2m+uF2m上.钱建发等人[10]将[7]的结论推广到环F2+uF2+u2F2.最近，Cengellenmis[11]定义了环F2+uF2+…+umF2(m=2s)上的Type II码，并研究了其Gray象的性质.

本文首先给出环F2+uF2+…+ukF2上任一偶长的自正交和自对偶码的构造方法，然后通过定义环F2+uF2+…+ukF2中的每个元素的Euclidean重量证明了环F2+uF2+…+ukF2上自对偶码是Euclidean重量为2k+2倍数的Type Ⅱ码.

2基础知识

设环

R=F2+uF2+…+ukF2，

其中uk+1=0.显然

F2+uF2+…+ukF2=F2[u]/(uk+1).

环R是一个最大理想是(u)的有限链环.任意的x∈R，x都可以唯一的表示为

x0+ux1+…+ukxk，

其中xi∈F2，i=0，…，k.

对于任意

x=(x0，x1，…，xn-1)，y=(y0，y1，…，yn-1)∈n，

定义它们的内积为

x·y=x0y0+x1y1+…+xn-1yn-1.

如果两个码字x·y=0，称这两个码字正交.对R上一线性码C，其对偶码C⊥是与C中的所有码字正交的所有向量的集合，即

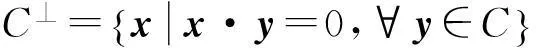
显然C⊥也是线性码.如果C⊆C⊥，称码C自正交.如果C=C⊥，称码C自对偶.如果码C可以通过置换它的坐标得到另外一个码C′，称这两个码置换等价.

R上任一线性码C都置换等价于如下矩阵所生成的码

其中li，0≤i≤k是正整数.Ai，j(0≤i≤k，1≤j≤k+1)是域F2上的矩阵.

定义R上线性码C的维数，定义为

dimC=log|R||C|，

其中|R|=2k+1.

3环R上偶长自对偶码的构造

由环R的特殊性知，在R中一定存在一个元素t使得t2=1，如12=1，(1+uk)2=1等等.这一事实将在下面构造R上偶长自对偶码中用到.

引理3.1[12]在环F2+uF2+…+ukF2上，当k是奇数时，环F2+uF2+…+ukF2上一定存在自对偶码；当k是偶数时，环F2+uF2+…+ukF2上存在自对偶码当且仅当码长n是偶数.

由上述引理知，不论k取何值，环R上一定存在偶长的自对偶码.下面给出环R上任一偶长的自对偶码的统一构造.

定理3.2设G0=(ri)是环R上长度为偶数n的自正交码C0的生成矩阵(不需要标准型)，其中ri是G0的行向量，1≤i≤r.设X=(x1，…，xn)∈Rn且在R中X·X=1.假设yi=X·(ri)，1≤i≤r，则由

生成的码是R上长度为n+2的自正交码.

证只需证G的任两行是相互正交的.

(i) 第一行显然是自正交的，因为在R里X·X=1，即X·X+1=0.

(ii) G的第一行正交于G的任(i+1)行，1≤i≤r-1.因为

(1，0，x1，…xn)·(yi，yi，(ri))=yi+(xi，…xn)·(ri)，

再根据假设yi+(xi，…xn)·(ri)=0.

(iii) G的任(i+1)行正交于G的任(j+1)行，1≤i，j≤r-1.因为在R里

yiyj+yiyj+(ri)·(rj)=0.

推论3.3设G0=(ri)是环R上长度为偶数n的自正交码C0的生成矩阵(不需要标准型)，其中ri是G0的行向量，1≤i≤r.设X=(x1，…，xn)∈n且在R里X·X=1.假设yi=X·(ri)，1≤i≤r，那么由

生成的码是R上长度为n+2的自正交码.

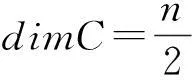
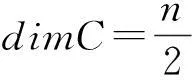
是一整数.

定理3.6设G0=(ri)是环R上长度为偶数n的自对偶码C0的生成矩阵(不需要标准型)，其中ri是G0的行向量，1≤i≤r. 设X=(x1，…，xn)∈Rn且在R里X·X=1.假设yi=X·(ri)，1≤i≤r，那么由

生成的码是R上长度为n+2的自对偶码C.

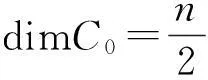
例3.1当k=2时，设

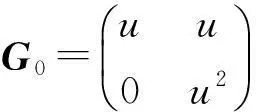
在环F2+uF2+u2F2上，由G0生成的码是长度为2的自对偶码.那么根据定理2.6，可以构造

生成长度为4的自对偶码.以此类推可以构造环F2+uF2+u2F2上任意偶长的自对偶码.

4环F2+uF2+…+ukF2上的TypeⅡ码

定义环F2+uF2+…+ukF2中的每个元素的Euclidean重量：0；1和1+u+…+uk-1+uk；u和u+u2+u3+…+uk；…；1+u+…+uk-1和1+uk；uk分别为0，12，22，…，(2k-1)2，(2k)2.一般地，对于任意x∈R，

x=x0+ux1+…+ukxk，

其中xi∈{0，1}，i=0，…，k，定义x的Euclidean重量为

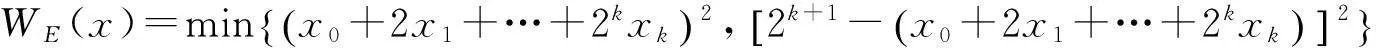
环(F2+uF2+…+ukF2)n上每个码字c的Euclidean重量记为WE(c)等于c的每个分量的Euclidean重量的和.定义环F2+uF2+…+ukF2上的TypeⅡ码为环F2+uF2+…+ukF2上所有码字的Euclidean重量是2k+2倍数的自对偶码.特别地，当k=0时，其为标准TypeⅡ码定义.

Φ∶(F2+uF2+…+uk+1F2)n→(F2+uF2+…+ukF2)n，

Φ(c1，c2，…，cn)=(c1(moduk+1)，c2(moduk+1)，…，cn(moduk+1)).

对(F2+uF2+…+uk+1F2)n上任一长为n的码C，记其在该映射下的象为Φ(C).

引理4.1环F2+uF2+…+uk+1F2上任一自正交码C的象的Euclidean重量是是2k+2倍数.

证设c=(x0，x1，…，xn-1)∈C，对于任意的xi∈F2+…+uk+1F2，xi均可以唯一地表示为xi，0+uxi，1+…+uk+1xi，k+1.即

xi=xi，0+uxi，1+…+uk+1xi，k+1

其中0≤xi，j≤1，0≤i≤n-1，0≤j≤k+1.由于c是自正交的.即

xi·xi=(xi，0+uxi，1+…+uk+1xi，k+1)2=0.

故当k是奇数时，WE(Φ(x))是2k+3的倍数，当k是偶数时，WE(Φ(x))是2k+2的倍数.

引理4.2设C是F2+uF2+…+uk+1F2上任一自正交码，则Φ(C⊥)⊆Φ(C)⊥.

证设v∈C⊥，则对任意的w∈C，都有v·w=0.所以，Φ(v)·Φ(w)=0.由v和w的任意性，可得Φ(C⊥)⊆Φ(C)⊥.

由引理3.1和3.2直接得到下面的结论.

定理4.3C是F2+uF2+…+uk+1F2上任一自正交码，那么Φ(C)是F2+uF2+…+ukF2上的自正交码并且其所有码字的Euclidean重量是是2k+2倍数.

定理4.4设C是F2+uF2+…+uk+1F2任一长为n的线性码且型为{l0，l1，…，lk+1}，则Φ(C)是F2+uF2+…+ukF2上长为n的线性码且型为{l0，l1，…，lk}.

证知C的任一码字是其生成矩阵的行向量的线性组合，则Φ(C)的任一码字是由C的生成矩阵的行向量的线性组合模去uk+1而得到.从而Φ(C)的生成矩阵是

则Φ(C)是F2+uF2+…+ukF2上的TypeⅡ码.

因此Φ(C)是自对偶的.由引理3.1，Φ(C)是TypeⅡ码.

[参考文献]

[1]Qian J， Zhang L， Zhu S. (1+u)-constacyclic and cyclic codes over F2+uF2[J]. Appl. Math. Lett.， 2006， 19: 820-823.

[2]Abualrub T， Siap I. Constayclic codes over F2+uF2[J]. J. Franklin. Inst.， 2009， 346: 520-529.

[4]Dinh H Q. Constacyclic codes of length 2sover Galois extension rings of F2+uF2[J]. IEEE Trans. Inform. Theory， 2009， 55(4): 1730-1740.

[5]Dinh H Q. Constacyclic codes of length psover Fpm+uFpm[J]. J. Algebra， 2010， 324: 940-950.

[6]Bonnecaze A， Udaya P. Cyclic codes and self-dual codes over F2+uF2[J]. IEEE Trans. Inform. Theory， 1999， 45 (4): 1250-1255.

[7]Dougherty S T， Gaborit P， Harada SoléP M. Type II codes over F2+uF2[J]. IEEE Trans. Inform. Theory， 1999， 45 (1): 32-45.

[8]Ling S， SoléP. Type II codes over F4+uF4， Europ[J]. J. Combinatorics， 2001， 22: 983-997.

[9]Bestumiya K， Ling S， Nememmzo F R. Type II codes over F2m+uF2m[J]. Discrete Mathematics， 2004， 275: 43-65.

[10]Qian J， Zhang L， Yin Z. Type II codes over F2+uF2+u2F2[J]. Processing of IEEE Information Theory Workshop， 2006:21-23.

[11]Cengellenmis Y. Type II codes over F2+uF2+u2F2+u3F2+…+umF2.Int. [J]. J. Contemp. Math. Science， 2010， 5(12): 595-602.

[12]汤道安，朱士信，唐永生. F2+uF2+…+ukF2上的自对偶码[J]. 合肥工业大学学报， 2010，33(3)： 478-480.

Type Ⅱ Codes Over F2+uF2+…+ukF2

WANGYong1,2

(1.School of Mathematics, Hefei University of Technology, Hefei 230009, China;

2. Feixi Middle School in Anhui Province, Hefei 231200)

Abstract:A method of constructing self-orthogonal and self-dual codes of any even length over F2+uF2+…+ukF2 is given in this paper. Euclidean weight of each element in F2+uF2+…+ukF2 is defined and self-dual codes over F2+uF2+…+ukF2 are proved to be Type II codes with Euclidean weights a multiple of 2k+2.

Key words: self-dual codes; self-orthogonal codes; euclidean weight; type Ⅱ codes