一道美国数学竞赛试题的解答及其思考

一道美国数学竞赛试题的解答及其思考

●钟劲松(湖南教育出版社湖南长沙410007)

美国数学天才选拔赛(USAMTS)是一项针对美国初、高中学生进行的免费的数学竞赛，该项比赛分3轮——初赛、复赛和决赛.所有参赛学生必须在1个月之内独立完成，学生可查阅资料，借助计算器和计算机等.该项比赛主要训练参赛学生分析问题、解决问题和规范表达的能力，对学生的洞察力、创造力和毅力都有很大帮助.本文选取第26届(2014~2015)第2轮比赛的第3题加以分析，用3种不同的方法进行解答，最后总结思考，旨在说明在立体几何的教学过程中，教师应从多角度、多方面审视题目，引导学生用多种方法去分析和解决问题，提高学生的学习兴趣.

题目已知四棱锥P-OABC底面四边形的4个顶点坐标为O(0,0,0)，A(3,0,0),B(3,3,0),C(0,3,0),顶点P的坐标为(1,1,3)，另一四棱锥与{P-OABC}共底，其顶点Q的坐标为(2,2,3)，求2个四棱锥公共部分几何体的体积.

分析1(解析法)求解本题的关键是要了解2个四棱锥公共部分的几何体形状，已知条件所给的图形是学生熟悉的几何体，但公共部分不是学生所熟悉的几何体形状，学生不知如何套用公式，也不知道套用哪个公式求体积.

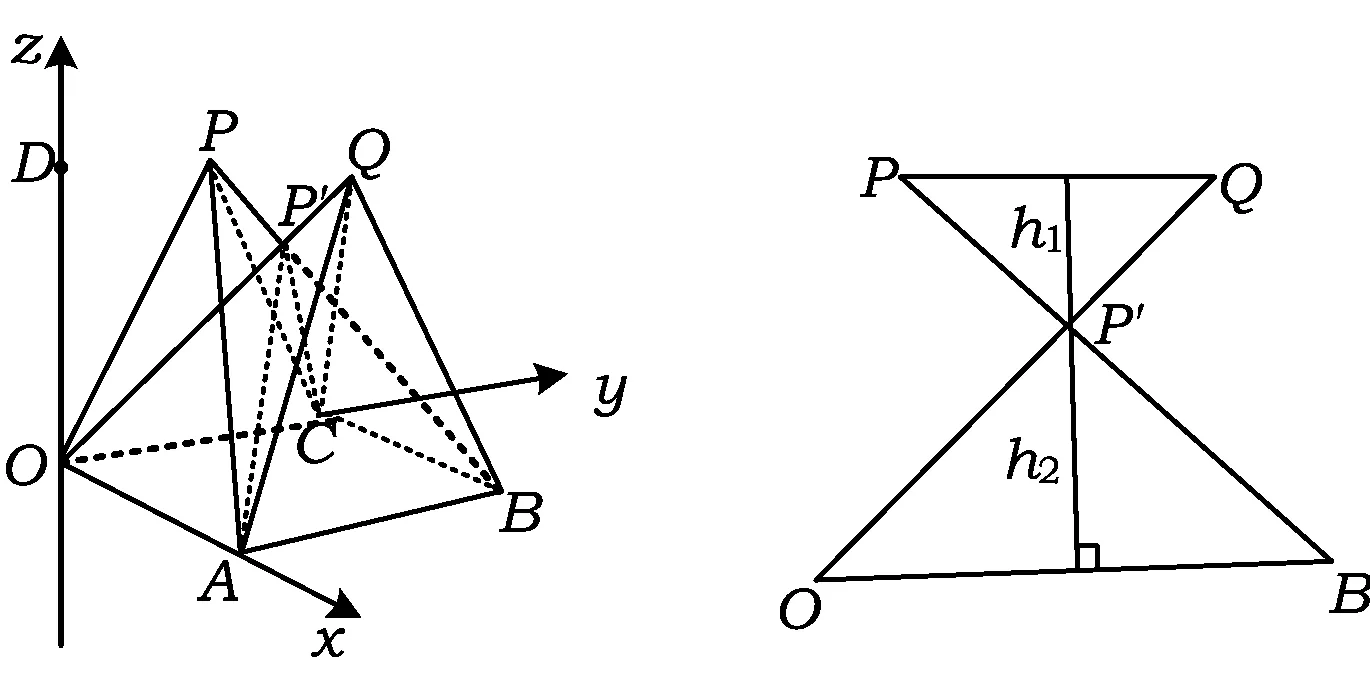
图1 图2

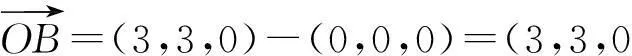
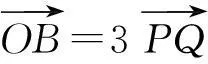
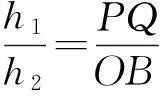
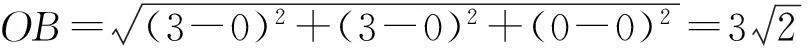
所以

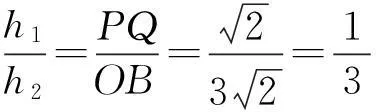
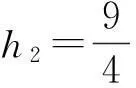
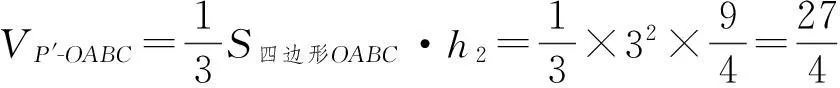
评注解法1通过空间中坐标的运算得知点P,Q,O,B共面，推知PB,OQ相交，从而得知相交的几何体为一四棱锥.在解答的过程中一定要注意论证平面POB与底面OABC垂直，否则不能够直接使用h1+h2=3.

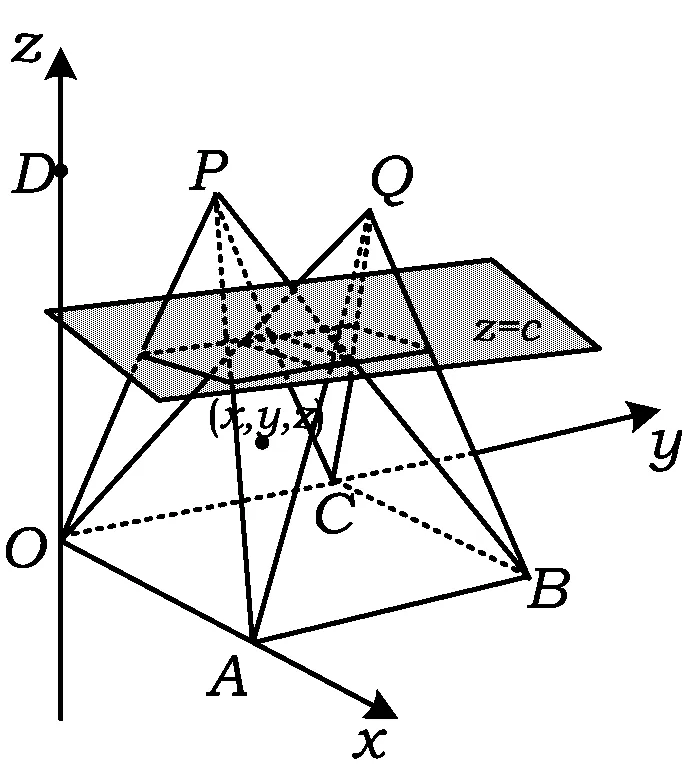
图3

分析2(不等式法)通过平行于底面的平面{z=c}(其中0≤c≤3)来截2个四棱锥，分别与2个四棱锥的8条棱相交于8个点，通过2个四棱锥公共部分点的坐标所满足的不等关系求解.

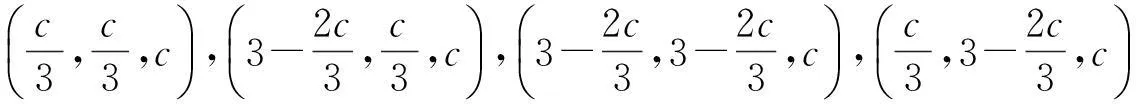
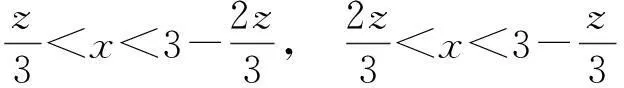
且

(1)

评注本方法思路新颖，通过简单的不等式运算，即可得知“临界”状态下z的值，从而求其体积.

分析3(向量法)由上面的分析可知，2个四棱锥相交部分构成一个新的四棱锥，新四棱锥的顶点为直线PB和QO的交点P′.

设M为线段PB上的任意一点，则

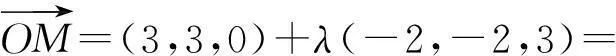
(3-2 λ,3-2 λ,3 λ),

因为点P′既在直线QO上，又在直线PB上，所以

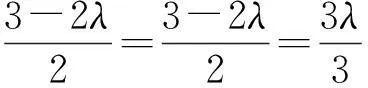
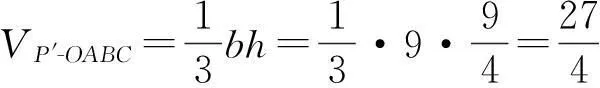
评注本解法使用了向量作为运算的工具，前提是已知2个四棱锥相交部分为一个新四棱锥.通过向量的简单运算，可以直接求出新四棱锥的顶点坐标，避免了解法1中繁琐的论证和运算.

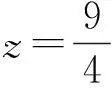
由此，笔者有以下4点思考：

1)立体几何知识主要考查学生的空间想象能力和运算推理能力.除了常规的考查(如点、线、面位置关系的性质与判定，简单计算几何体的表面积、体积以及异面直线的夹角、直线与平面所成的角、二面角等计算)外，笔者认为应增加一些考查空间想象能力的题目，充分发挥学生的想象能力.

2)立体几何与不等式，看似关联度不高的知识点，只要勤于思考，它们之间也可以嫁接，产生美妙的解答.我们在平常的解题训练中，要从不同的方面去思考问题，去发掘优美的解答，每一种解法都代表一种思考问题的角度.

3)高考和自主招生作为选拨人才的一种考试，势必会在题目的难度上设置一定的梯度.笔者认为，以后的考试会逐渐增加一些不常规的题目，“多考一些想，少考一些固定套路的算”.

4)数学的思维过程是“观察—抽象—猜想—论证”，教师在教学过程中要带领学生遵循数学的思维过程，带领学生一起去探索、思考问题.平时在教学过程中发现很多学生有“懂而不会”的现象，实际上学生不是真的“懂”，而是被迫地接受和记忆知识，没有探究的过程.因此，为了取得好的教学效果，教师和学生必须共同参与，去探究、发现数学的美.