研一题 悟一法 通一类——一节高三试卷讲评课的课堂实践与启示

研一题悟一法通一类——一节高三试卷讲评课的课堂实践与启示

●金明叶东芳(广州市真光中学广东广州510380)

1问题提出

试卷讲评课是高三教学的一种常见课型.高质量的讲评课可以矫正学生在答题过程中暴露出的问题，深化对知识的理解，弥补不足，提升以思维品质为核心的各种能力与素质.然而试卷讲评课中经常出现这样的现象：上课时教师讲得滔滔不绝，学生却听得昏昏欲睡；教师希望在课堂上多讲一些题，让学生领悟多一点，但教学效果却未必如此.甚至常常出现事与愿违的现象，教师讲得越多越快，学生领悟得越少.有的试题，同类题目已讲过4~5遍，但学生还是出错.究其原因可能是学生对试题所要运用的方法没有理解，没有对试题进行深入地研究.也可能是教师贪多求快，对试题的剖析不够深刻，没有激起学生的学习兴趣.

为此，笔者在试卷讲评课尝试着：研一题(即认真研究一道题或几道变式题)，悟一法(使学生领悟和掌握该类题目所蕴含的思想方法)，通一类(通过设计练习题，使学生再研究以达到掌握一类题的目的).课堂教学的重点放在研一题上，为此需要确定那些题值得研究，从哪些角度研究，从而使学生理解与掌握解决这类题目的方法.以下是笔者对广州市一模一道试题的课堂教学实践.

2课堂教学实践

2.1研一题

2.1.1确定值得研究的问题

什么题值得研究是研一题的起点，也是研一题的核心与关键.值得研究的题目具有以下特征：学生易混、易错，考查的是学科的主干知识，蕴含着重要的数学思想方法；通过解答此题能提高学生分析问题、解决问题的能力；解决此问题的方法是通性通法，而不是特殊技巧等.

本节课我们选取了广州市2015年一模解析几何综合题第2)小题：用参数法求轨迹.此题学生得分极低，是学生学习的难点.通过此题的研究分析，可让学生领悟用参数法求轨迹的方法与步骤，增强消参意识，提高学生分析问题与解决问题的能力.

1)求椭圆C1的方程；

2)求点Q的轨迹方程；

(2015年广东省广州市一模试题)

2.1.2研究问题的视角

视角1学生的错误或失败解法研究

学生的问题和错误是教学的重要资源，是高三讲评课的重点与关键.研究学生的错误，能找出学生理解问题的疑难点或教师教学的遗漏点，为修补学生缺漏、增长知识、提高学生能力作准备.

即

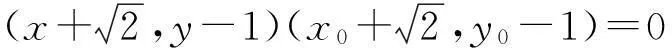
从而

(1)

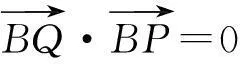
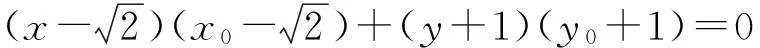
(2)

式(1)+式(2)得

式(1)-式(2)得

师：这是我们很多同学的解法，现在请同学们分析一下其成功与失败之处.

生1：将向量语言转化为坐标运算，得出式(1)和式(2)都是对的，并试图将式(1)和式(2)相加或相减消去参数x0,y0，但却没有消去参数x0,y0，也没求出点Q(x，y)的轨迹方程.

师：生1分析得很好，该同学知道先设定参数，依条件列出关系式(1)和式(2)，并试图用常用的相加或相减去消参，但是没有求出轨迹.那么此题要求我们做什么？怎么做？还有什么条件没用吗？

生3：求x，y的关系需要消去参数x0,y0，理论上,方程(3)和(4)与椭圆方程联立应该可以消去x0,y0，但不知怎么消？

师：同学们的分析有道理，求点Q的轨迹，关键是消去参数x0,y0，我们将这种求轨迹的方法叫参数法.参数法求轨迹的重点是消参，如何合理消参，是本节课研究的重点之一.

教学感悟教学一开始，展示学生的解法，让学生去观察、去发现、去评说解法中的闪光点与不足之处.这样学生的解题思路暴露在大众面前，既可以在学生的错误解法中发现问题，又可以在错误中发现闪光点,有利于激发学生的学习热情，调动其学习的积极性.

视角2消参方法的研究

生(众)：沉默.

师：可行吗？

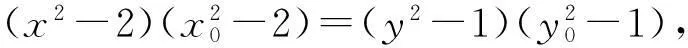
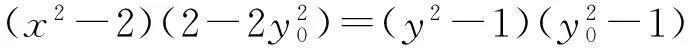
2x2+y2=5.

师：经过共同探究，解决了消参的问题.其实消参的关键是要用上已知条件，观察分析如何变形以达到消参的目的.

教学感悟在教师的引导下,学生经过努力找到了消参的方法.在教学过程中，教师重在启发诱导，让学生动手动脑思考、探索、实践；在细节的处理上,教师采用追问的方式，让学生自己修正错误.

视角3轨迹的完备性研究

师：我们已消去了参数，求得轨迹方程为{2x2+}y2=5，还需思考一下，方程2x2+y2=5上的每一个点是否都是点Q的轨迹？请大家小组合作探讨，重点分析题目条件有没有用完.

生7：点P异于点A,B这个条件怎么用？

师：很好，生7很敏锐，提出的问题很好，有同学能解答吗？

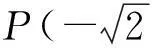
师：由此同学们可总结一下如何探究轨迹的完备性.

生9：重新审题，看题目条件是否用完，特殊检验即可.

教学感悟用参数法求轨迹的难点是如何探讨轨迹的完备性.在教师的提示下，学生经过小组合作讨论找到了求轨迹完备性的方法并总结出解题的常用方法.

视角4多种解法的研究

一题多解是解决问题的重要方法，它可培养学生思维的广阔性、灵活性，对培养学生的思维品质有极大的帮助.

师：还有其他不同的解法吗？

众生沉默.

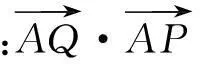
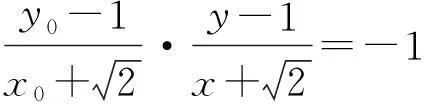
(5)

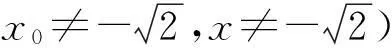
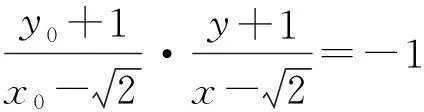
(6)

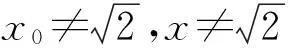
师：生10做得非常好，将向量点乘为0说明2条直线互相垂直，转化为斜率乘积为-1，用这种转化可能更容易想到如何消去参数.

教学感悟一题多解可沟通知识联系，开阔学生思维，培养学生思维的广阔性，是提升学生思维能力的重要方法.

视角5变式探究

师：前面我们探讨了参数法求轨迹的问题，重点解决了如何消参的问题，并探讨轨迹的完备性.既然是参数法求轨迹，那么如何设参、引参也需要探究，为此我们研究以下变式题.

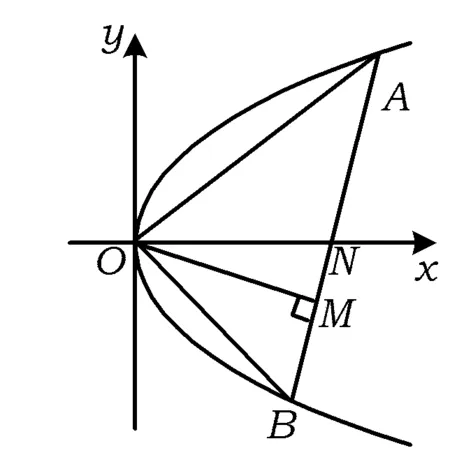
图1

变式题如图1所示，设点A和B为抛物线y2=4px(其中{p>}0)上原点以外的2个动点，已知OA⊥OB,OM⊥AB,求点M的轨迹方程，并说明它表示什么曲线.

师(学生思考了10分钟):思考了这么长时间，有做出来的吗？

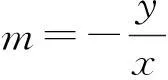
y2-4pmy-4pa=0,

从而

y1+y2=4pm,y1y2=-4pa,

于是

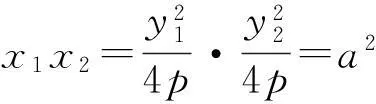
由OA⊥OB知

x1x2+y1y2=0,

从而

a2=4pa,

得

a=4p,

故

消去m,得x2+y2-4px=0(其中x≠0).

师：生11采用的是设直线AB的方程，利用条件消去参数m,从而求得点M的轨迹方程为x2+y2-4px=0(其中x≠0)，还的别的方法吗?

生12:(设参方式2)直线OA的方程为y=kx(其中k≠0),则

得

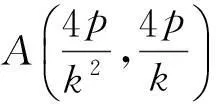
直线OB的方程为

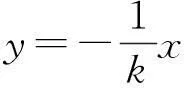
与y2=4px联立,得A(4pk2,-4pk).

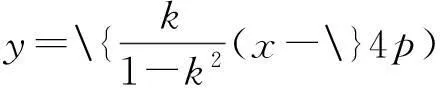
当k=±1时，直线AB方程为x=4p，过定点{N(4p，}0).

由OM⊥AB得M在以ON为直径的圆上(点O除外)，故动点M的轨迹方程为

x2+y2-4px=0(其中x≠0).

师：生12是设直线OA的方程为y=kx，根据条件也得出了结果.还有别的方法吗?

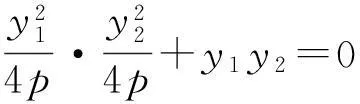
从而

y1y2=-16p2,

得

直线AB的方程为

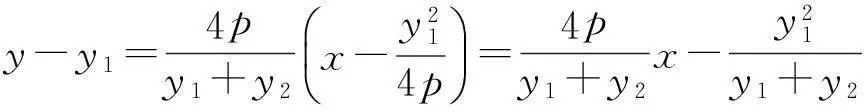
即

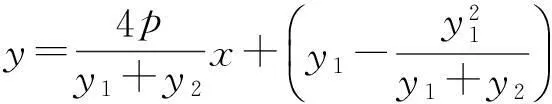
可得

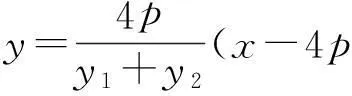
(7)

由OM⊥AB知，

由式(7)和式(8)得

x2+y2-4px=0(其中x≠0)

师：非常好，刚才3位同学分别用设直线AB的方程、设直线OA的方程以及设点A,B的坐标3种设参方式解答了此题.通过这2道题的研究，对参数法求轨迹，你能归纳一下怎样解题吗？

2.2悟一法

生14：我认为用参数法求轨迹先要设参数，然后消参数.

生15：还要考虑轨迹的完备性，考虑完备性有点难.

生16：考虑完备性我认为主要利用题目条件，看有什么条件没用，如例1中，P是异于点A,B的点，只需验算当点P与点A,B重合时，它的坐标是什么即可.还可以从式子本身的范围考虑，如分母不为0等.

2.3通一类

师：刚才我们研究了用参数法求轨迹的2道题.同学们能否真正掌握这种方法，下面2道题供同学们课后研究、探讨.

课后作业

(说明：课后作业1的重点是消参与探究轨迹的完备性，难点在如何探究轨迹的完备性；作业2的重点是设参与消参，有一定的难度.通过这2道题的研究能理解与掌握消参法求轨迹的方法，以达到通一类的目的.)

3教学启示

试卷讲评课如何讲？是泛泛而谈还是重点突破.通过本节课的教学实践和与同组教师交流反馈等，大家形成了共识，有几点感想与同行分享，供参考.

1)试卷讲评课要研究重点题，使学生悟一法，通一类.

试卷讲评课如何吸引学生，使学生愿听、愿想、愿探究.教师所选择的需要研究的题目要有示范性.课堂上通过重点题的研究，能辐射到多种思想方法或能起到构建知识框架的作用,或能够揭示一般性的解题方法，从而达到教学效益的最大化.通过研究重点题，使学生悟到解决一类题的方法与注意事项.本节课的教学目标明确，以一道广州一模试题及变式题为范例，师生共同探究，研究了用参数法求轨迹的方法及注意点.学生在探究中充满了激情，不知不觉地加强了方法的理解与应用.

2)课堂研究的习题要少而精.

例题过多就会增加学生入题时间，选择少而精的研究题既能减少学生思维的断层，教师可通过探究、变式、一题多解等手段，加强学生思维的连续性，从而调动学生学习的积极性，这就需要教师在选题上下功夫，在例题的解题教学分析上下功夫，找准课堂的主攻方向，是通过问题探究激发学生的兴趣，还是通过一题多解构建思想方法，或是通过问题回顾来还原知识体系.

3)研一题，悟一法，通一类是课内课外的有机结合.

研与悟在课堂上完成.课堂上通过师生共同的研，以达到学生的悟.而要通一类还需学生课后作业来巩固，需继续研究，培养学生的探究意识与研究意识.