两种反求电容储能轨道炮时序方法的比较
2016-01-06张洪海,程广伟,国伟等
两种反求电容储能轨道炮时序方法的比较
张洪海1,程广伟1,国伟1,文枫2,李明涛1
(1.西北机电工程研究所, 陕西 咸阳712099;2.中国兵器科学研究院,北京100089)
摘要:依靠多个商业软件间的集成来完成轨道炮系统级仿真及优化不但复杂,而且还存在两个缺点,一是有限时间内,优化所采用的遗传优化算法不能保证最优且结果不可重现;二是电源的拓扑结构需要手工调整脉冲,寻优过程无法彻底的自动化。目前,轨道炮系统级轨道炮仿真代码和电容储能轨道炮PFN触发时序反求问题都少见文献报道。为求解此问题,将多维的触发时序优化问题转化为一维的延迟时间确定问题,从而使全局迭代法可用。应用所开发的求解及优化程序,给出了遗传优化算法及全局迭代法求解该问题的结论及比较结果。建立了电容储能轨道炮数学模型,分析了轨道电流这一参数的重要性,介绍了由轨道电流平顶波幅值反求PFN触发时序问题的意义。通过定义理想时序的概念,说明了迭代法的“细分-逼近”特性,指出迭代法可用于解决由炮口初速反求触发时序问题。
关键词:电磁轨道炮;系统级仿真;集总参数模型;时序
中图分类号:TJ866 文献标志码: A
收稿日期:2014-02-18;修回日期: 2014-09-01
作者简介:张洪海(1975- ),男,硕士,主要从事特种机械仿真及设计工作。E-mail:z931014@163.com
Comparation of Two Methods on Calculating Timing Sequence of
Capacitor Based Railgun
ZHANG Honghai1, CHENG Guangwei1, GUO Wei1,WEN Feng2, LI Mingtao1
(1.Northwest Institute of Mechanical & Electrical Engineering, Xianyang712099, Shaanxi, China;
2.Academy of China Ordnance Science, Beijing100089, China)
Abstract:To simulate and optimize the railgun system by integrating multiple kinds of commercial software is inconvenient, and may bring two shortcomings. Firstly the genetic optimization algorithm can hardly found the best and repeatable results in certain time, secondly topological structure of PPS must be adjusted manually, so that the optimization process can not be completely automated. Till now, simulation code and reverse problem for PFN trigger ti-ming sequence of railgun have been seldom introduced. In this paper, mathematic model of capacitor-based railgun was established and the importance of the rail current was analyzed. By translating the problem of the multi-dimensional timing sequence optimization into a problem of one-dimensional delay-time confirmation, the global iteration method was available. Applying the solving and optimization program developed, timing sequence results based on iteration method and GA method were given and compared. Through defining the concept of ideal timing sequence, the subdivision-approximation property of iteration method was introduced, which can be used to solve timing sequence problems with a given muzzle velocity.
Key words:electromagnetic railgun; system-level simulation; lumped parameter model; timing sequence
轨道炮相对于传统火炮的一个优点是发射过程可控,对于电容储能轨道炮,通过调节脉冲成型网络(PFN)触发时序,轨道炮可以工作在不同的发射状态,实现不同的发射效果。
采用较小脉宽、较高幅值的输出电流可以提高轨道炮的效率,但当输出电流幅值为兆安级时,轨道之间通常会存在数十兆牛顿或更高的斥力。一旦发射过程中的轨道斥力过大,将可能导致接触失效从而降低效率,甚至影响安全,而这种斥力与电流的平方存在近似正比的关系。由于轨间斥力、发射效率均受轨道电流的影响,因而轨道能够通过的最大电流是比发射效率和炮口初速更加基础的设计指标。在不考虑轨道设计通流能力的情况下,研究系统的最大效率是无意义的。综合考虑,通常希望轨道电流为一平顶波,且其幅值尽可能接近轨道的最大通过电流。这样,如何排布PFN时序,使得轨道电流为某一幅值的平顶波就成为轨道炮设计和试验时经常面对的问题。笔者将介绍由给定平顶波幅值反求电容储能轨道炮时序问题的两种方法:遗传优化方法及迭代法,并对两种方法的性能进行了对比和讨论。
1轨道炮及其仿真技术
轨道炮的基本理论问题(如多物理场分布、刨削和烧蚀等)大多涉及到偏微分方程(PDE)的建模及求解。除商业FEM软件外(如ANSYS[1-2]),研究者们还开发了一些专门用于轨道炮仿真的有限元程序,其中最著名的是EMAP3D,该程序是电磁、结构、热耦合并行的三维有限元仿真软件,可以建模、分析滑动电接触机理[3-4],并已获得大量的研究成果[5-6]。
系统级仿真通常涉及到由ODE组成的集总参数模型(LPM),这些模型一般使用试验或半试验参数(公式)来简化空间分布的变量。通过持续改进参数(公式),这些模型可以在一定的精度下预测系统性能。由于求解迅速、便于优化,LPM通常被用于系统总体设计。1982年,Deadrick推导了轨道等效电阻率公式,针对磁通压缩发电机驱动的轨道炮,开发了用于求解非线性时变轨道炮模型的仿真代码[7]。近年来公布的系统级轨道炮仿真的工作大多是基于商业软件或平台的。文献[8]建立了考虑了接触效应和速度趋肤效应(VSEC)的系统级轨道炮仿真模型,并认为仿真结果与试验的速度误差在5%以内。该模型分别建立在Simplorer V8和Matlab/Simulink中,应用该模型和iSight软件内置的多目标遗传优化算法,来寻找最优的弹丸质量和触发时序。文献[9]基于HLA建立了系统级轨道炮仿真平台。
依靠商业软件间的集成来完成轨道炮系统级仿真及优化不但复杂,而且还存在两个缺点:一是有限时间内,优化所采用的遗传优化算法不能保证最优且结果不可重现;二是需要手工调整脉冲电源的拓扑结构,寻优过程无法彻底的自动化。
目前,轨道炮系统级轨道炮仿真代码和电容储能轨道炮PFN触发时序反求问题都少见文献报道。
2电容储能轨道炮模型及求解
电容储能轨道炮组件如图1所示,其中脉冲功率电源(PPS)由一定数量的脉冲成型单元(PFU)构成。发射时,PFU内的电容被充电到某一电压,而后PFU按照给定的时序放电。当电流流经轨道和电枢时,电枢在电磁力作用下沿着轨道加速运动,并最终脱离炮口完成整个发射过程。通过调整PFU的触发时间,PPS可以输出不同的电流波形,这种PPS也被称为脉冲成型网络(PFN)。

理论上,由任意数目电容模块组成的脉冲电源都可以作为轨道炮电源。
2.1 PFN数学模型
图2为一个典型的PFU结构图。图中R1、R2为线缆电阻,N0~N5为电路节点, i15、i20、i30、i42、i43、i54为带参考方向的支路电流。
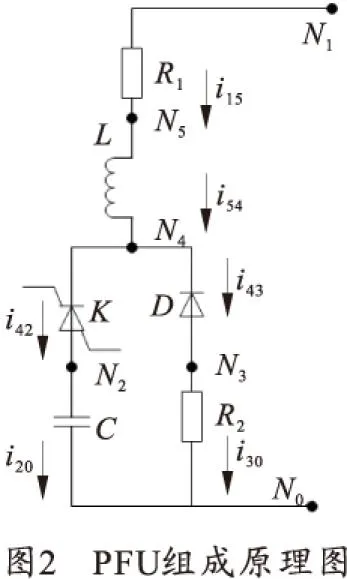
PFU中,每个支路可以应用参考方向列出如下方程:
(1)
(2)
u3-u0=i30R2
(3)
u5-u1=i15R1
(4)
(5)
(6)
式中,Rc为接触电阻。
根据基尔霍夫电流定律,有:
i54=i15
(7)
i54=i42+i43
(8)
i42=i20
(9)
i43=i30
(10)
这样,多个并联在N1、N0节点上的PFU可以组成一个完整的PFN,在仿真过程中,以一个足够大的电阻来表示二极管及硅堆的开路状态。
2.2 轨道-电枢集总参数模型
考虑热效应和电流趋肤效应,轨道和电枢可被建模为电路的支路[8],其电路模型如图3所示。图中Rm为炮口短路电阻,Ra与Rc分别为电枢电阻和接触电阻;Rvsec为VSEC电阻;N0~NA为电路节点; i9A~i16为带参考方向的支路电流。

图3中的变量遵守式(11)~(17)中所列公式。
(11)
(12)
(13)
Rvsec=Rvcv1.5
(14)
Rvsec1=pRvsec
(15)
Rvsec2=(1-p)Rvsec
(16)
Lr=xL′
(17)
式中: x为电枢位移;Rr为轨道电阻;lr是轨道长度;h是轨道高度;s是电枢宽度;Kr、Ka、Kc为材料相关的常数;v为电枢速度;Rvc为比例常数;p为决定VSEC电阻中与轨道接触部分(Rvsec2)和与电枢(Rvsec1)接触部分的比例系数;Lr为轨道电感;L′为电感梯度。
再次应用基尔霍夫电流定律,有:
i16=i67=i78=i89
(18)
i89=i90+i9A
(19)
iA0=i9A
(20)
根据每条支路的电压电流关系,有:
u1-u6=Rri16
(21)
u6-u7=Rci67
(22)
u7-u8=Rvsec2i78
(23)
(24)
u9-uA=Rvsec2i9A
(25)
uA-u0=RaiA0
(26)
u9-u0=Rmi90
(27)
令f、m分别为电枢的受力与质量,则电枢运动方程如下:
(28)
(29)
(30)
这样,在补充N1、N0点的电流平衡方程及给定N0点电压之后,PFN模型与轨道-电枢模型方程封闭,通过数值分析即可获得轨道炮的总体指标及性能。
2.3 轨道炮仿真程序
考虑到电容储能轨道炮可能采用任意数目的PFU,首先开发了可以求解任意维数的ODE数学模型的数值分析模块,该模块应用了一个精度控制的变步长、多步隐式ADAMS算法。在数值分析模块的基础上完成了电容储能的轨道炮仿真程序的开发工作,在仿真过程中,电路模型、轨道-电枢模型极其所对应的ODE方程组可以自然地表达。
为了测试软件的轨道炮仿真能力,应用所开发的代码对文献[8]中的一个轨道炮仿真算例进行了仿真验证。该模型采用了分为10组共28级PFU和简单的轨道形式,仿真中使用了相同的仿真参数和线缆电阻的调整范围,并从文献[8]的图6中反求了所需常数。通过计算得到了电枢速度为1 684 m/s,与文献[8]中的仿真结果1 686 m/s相符合。两种仿真轨道电流如图4所示。考虑到本软件的精度已经得到验证,因而可以认为仿真误差是由于设置了不同的线缆电阻造成的。
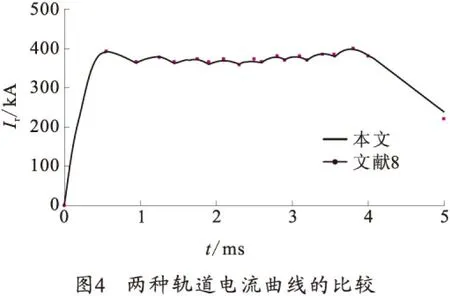
通过对包括轨道炮在内的多个算例进行对比分析,可知所开发的代码可以用于求解电容储能轨道炮仿真。
3电容储能轨道炮时序排布问题
为了找到能够提供某一平顶波轨道电流的时序,轨道发射装置(与其PPS一起)需要被仿真许多次。手工调节多级脉冲电源的时序非常费时,尤其是当存在数十、数百级以上的PFU时,调优工作是非常枯燥和不可想象的。由于笔者的核心代码全部自主开发,因而上述过程可以实现彻底的自动化。
为方便讨论,定义所使用的理想时序的概念。理想时序是指:对于给定的电容储能轨道炮及给定的PFU触发次序,某时序下所形成的轨道电流的多个极大值点都小于等于某给定值,记与给定值相同的极大值点的个数为Np,如果无法通过调整时序使Np增加,则此时序称为给定轨道电流平顶波幅值所对应的理想时序,简称理想时序。理想时序定义的内涵是在轨道受力得到限制的情况下,能够获得最高发射效率的时序。
基于2.3节中介绍的模型来阐述两种排布方法,一种是基于遗传算法的排布方法;另一种是全局迭代法,其目的是获得可以提供400 kA轨道电流平顶波的触发时序。
3.1 遗传优化方法
首先使用了标准的遗传优化算法来排布轨道炮时序,每一代种群中的每个个体为一个由随机数组成的列表,该表的元素被不同的比例算子映射到可行的时间范围之内,形成一个时序。每个时序在被轨道炮程序仿真后,都会得到不同的轨道电流波形。适应度函数以仿真结果与给定幅值为变量,定义如下:
(31)
式中: i为轨道电流;p是电流波形峰值点;np为峰值点个数;G是给定平等波幅值;g为抑制波形低于给定幅值的惩罚系数,
(32)
标准遗传算法中的参数设置如下:个体数为200;代数为6;交叉率为0.9;变异率为0.4; 精英比率为0.1。整个优化过程7 h内结束(仿真环境为:Intel 3.0 GHz双核CPU、2G内存、JDK1.6及默认虚拟机设置),注意到适应度函数可以被包装为分布式对象,因而该遗传优化过程可以被简单的并行起来。
3.2 迭代法
另一种方法是使用迭代的方式来寻找时序。算法流程如图5所示。

在该方法中,首先初始化了迭代步长,同时为每个PFU设置的足够大的触发时间以表示开路。在循环迭代过程中,如果仿真电流超出了给定值,则最后一级导通的PFU的触发时间将被推迟,否则该时间被设为下一级的触发时间,并开始下一次循环。
在考虑多维参数空间的优化的问题时,采用全空间遍历的迭代法通常是非常耗时的,但通过将问题转化为最后导通PFU的触发时刻的寻找问题,使得迭代法的参数空间降为一维,从而显著降低了全局迭代的时间。在迭代步长为50 μs的情况下,在相同的仿真环境下,该迭代过程在0.5 h内结束。
4仿真结果分析
图6给出了两种时序下的轨道电流曲线。

迭代法相对于遗传优化算法具备以下优点:
1)获得了更好的计算结果。
2)概念和实现都较为简单。
3)使用了更少的计算时间。
4)当迭代算法及步长固定时,迭代法所获得的时序将能够被重复获得,而遗传优化算法每次获得的时序都可能是不同的。
表1展示了通过迭代法(50 μs步长)和遗传优化法所得到的时序及该时序下的炮口初速对比。

表1 遗传优化法与迭代法的仿真结果对比
迭代法的另一个重要特点是:通过细分迭代法步长,所获得的时序将会逼近理想触发时序。例如,在采用10 μs步长进行迭代的情况下,炮口初速提高到了1 758 m/s,且轨道电流峰值分布在397~400 kA范围内,而当迭代步长为50 μs时,轨道电流峰值分布在375~400 kA范围内。图7给出了采用10 μs步长时迭代结果所对应的轨道电流曲线。可以看出,细分后所获得的时序更加理想,发射效率更高。

这个“细分-逼近”特性十分重要。从图6可以看出,遗传法与优化法都没能获得理想时序,但都提供了比文献[8]中算例更好的仿真结果,表面上看,在工程应用中都可接受,然而在轨道炮武器系统论证及设计中,由炮口初速反求触发时序将是轨道炮火控系统的重要工作,其特点是炮口初速误差必须控制在很小的范围内(微小的初速扰动将会带来很大的射击误差),这要求轨道炮触发时序必须十分精确。在平顶波、精确时序、给定初速、保证计算效率的要求下,迭代法的这种“细分-逼近”特性,使其成为解决该问题的基本工具之一。
5结论
电容储能轨道炮的触发时序对发射时轨道电流的影响十分显著。针对由轨道电流平顶波幅值反求PFN触发时序的问题,笔者给出了一种求解该问题的迭代法。通过与经典遗传优化算法的计算结果进行比较与分析,说明了本方法的优点。特别地,通过讨论迭代法的“细分-逼近”特性,说明了本方法能够用于由炮口初速反求触发时序问题的求解。
参考文献(References)
[1]COFFO M I R, GALLANT J, Modeling of the contact resistance and the heating of the contact of a multiple brush projectile for railguns with the final element code
ANSYS[C]∥Proceedings of the IEEE 17th International Pulsed Power Conference. Washington D C: IEEE, 2009:753-756.
[2]LIU Yuanqing, LI Jun, CHEN Duo, et al. Numerical simulation of current density distributions in graded laminated armatures[J]. IEEE Transactions on Magnetics,2007,43(1):163-166.
[3]FAIR H D. Advances in electromagnetic launch science and technology and its applications[J]. IEEE Transcations on Magnetisc,2009,45(1):225-230.
[4] FAIR H D. Electric launch science and technology in the united states[J]. IEEE Transactions on Magnetics,2003,39(1):11-17.
[5]STEFANI F, MERRILL R, WATT T. Numerical modeling of melt-wave erosion in two-dimentional block armatrues[J]. IEEE Transactions on Magnetics,2005,41(1):437-441.
[6]KIM B K. Effect of rail/armature geometry on current density distribution and inductance gradient[J]. IEEE Transactions on Magnetics,1998,35(1):413-416.
[7]DEADRICK F, HAWKE R, SCUDDER J. MAGRAC:a railgun simulation program[J]. IEEE Transactions on Magnetics,1982,18(1):94-104.
[8]YU Xinjie, FAN Zhaonan. Simulation and two-objective optimization of the electromagnetic railgun model considering VSEC resistance and contact resistance[J]. IEEE Transactions on Plasma Science,2011,39(1):405-410.
[9]MA Ping, HU Yuwei, YANG Ming, et al. System-level simulation approach and platform for electromagnetic railgun system[C]∥16th International Symposium on Electromagnetic Launch Technology.Beijing:EML,2012:1-5.
