控制变量对蒙特卡罗法期权定价的改进

丁照东+黄依慧

【摘 要】期权定价是一种价值最大化过程，根据不同时期不同股价的路径获取收益的最大值，并且考虑资产的时间价值。基本假设是股价波动符合几何布朗运动（Geometric Brownian Motion），这些波动可以用偏微分方程来描述。对于欧式期权来说，存在偏微分方程的解析解，通过Black-Scholes模型可以得到。期权定价可以运用蒙特卡罗法进行模拟估算，均值与解析解比较接近。尽管如此，模拟估算的过程仍存在比较大的缺陷，比如价格方差过大，置信区间无效等。这些缺陷可以通过改良蒙特卡洛方法来进行弥补。

【关键词】期权定价；蒙特卡洛法；方差缩减技术；控制变量

一、 背景

首先我们需要温习蒙特卡洛法进行欧式期权定价的过程：

（1）获得T时间内的股价路径，可以认为时间T的时候期权到期

（2）获得T时间点上的收益 ，其中 为T时间点上的股票价格，K为欧式期权的行权价

（3）考虑时间价值，将收益折算成现价，即为一个可能的期权价格

（4）重复上述（1）（2）（3）步骤n次，获取n个可能的期权价格

（5）取这n个可能的期权价格的平均值，即为蒙特卡罗法估计的期权价格

上述五个步骤的数理和编程逻辑可以简化为：

For i = 1，2，…，n

生成标准正态分布的随机数 Zi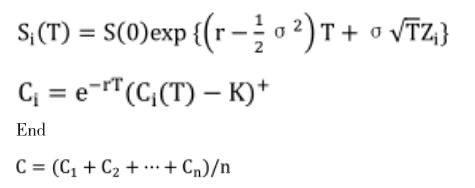

以上并非标准的编程语言，仅表示编程逻辑，其中字母S系列代表股价，S（0）是股票初始价格，r是利率，字母C系列是期权价格，K是行权价，T是当前欧式期权距离到期日的时间，σ是股价波动率，Zi来自于Black-Scholes模型中的随机量，假设为标准正态分布。

实际上，对于期权定价来说，蒙特卡洛是比较粗糙的方法，尽管可以得到一个比较满意的平均值，但是计算过程中期权价格Ci的方差大得惊人，更不用说置信区间。在后续的讨论中，我们可以从数据和图像上看到这一点。

二、改良蒙特卡洛法：方差缩减技术

方差缩减技术是对蒙特卡洛方法的优化，引入方差缩减技术的目的就是减少蒙特卡洛计算过程中Ci的方差，收缩置信区间，增加计算的精准度。当然方差缩减技术有多种，比如，控制变量（control variates， CV）、对偶变量（Antithetic Variates， AV）、分层抽样（Stratified Sampling， SS）、拉丁超立方抽样（Latin Hypercube Sampling， LHS）、矩匹配（Moment Matching， MM）和重要性抽样（Importance Sampling， IS）。本文中我们采用控制变量的方法，该方法的核心思想是引入另外一个变量，此变量的期望值可以通过解析式的形式计算，也就是与样本变量之间存在关系；根据引入变量可以得到一个估计值，该估计值与样本变量得到的估计值之间也存在关系，这样的关系可以用b来表示。用数学的语言来阐述就是：

（1）假定Y1，Y2，…Yn为样本观测值，独立同分布，我们的目标是估计Yi的期望E[Yi]，普通的无偏估计法是计算Y1，Y2，…Yn的算术均值；

（2）控制变量法是引入另一个变量Xi，并且Xi的期望已知，Xi与Yi之间存在如下关系：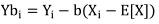

从而得到一个新的带估计变量Ybi，其中b为一个实数。不难看出，无论b取何值，Yb和Y的期望是相等的，所以这个变换不影响蒙特卡洛方法的均值结果，重点在于中间过程所有Yi值的方差。我们已经知道Yi的方差非常大（正如前文的Ci），目的是让新的估计量Ybi的方差尽可能的小。

（3）通过计算不难得到Yb和Y方差的关系：

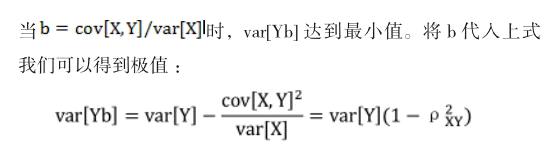
所以，问题又回到我们构建的变量X与原有样本变量Y之间的关系，相关系数越是接近于1，我们得到的结果越好。

三、控制变量（control variates）在期权定价中的应用

我们已经知道欧式期权定价中，股价Si是样本变量，目标是估计期权价格，那么我们针对Si引入如下变量：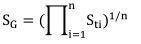

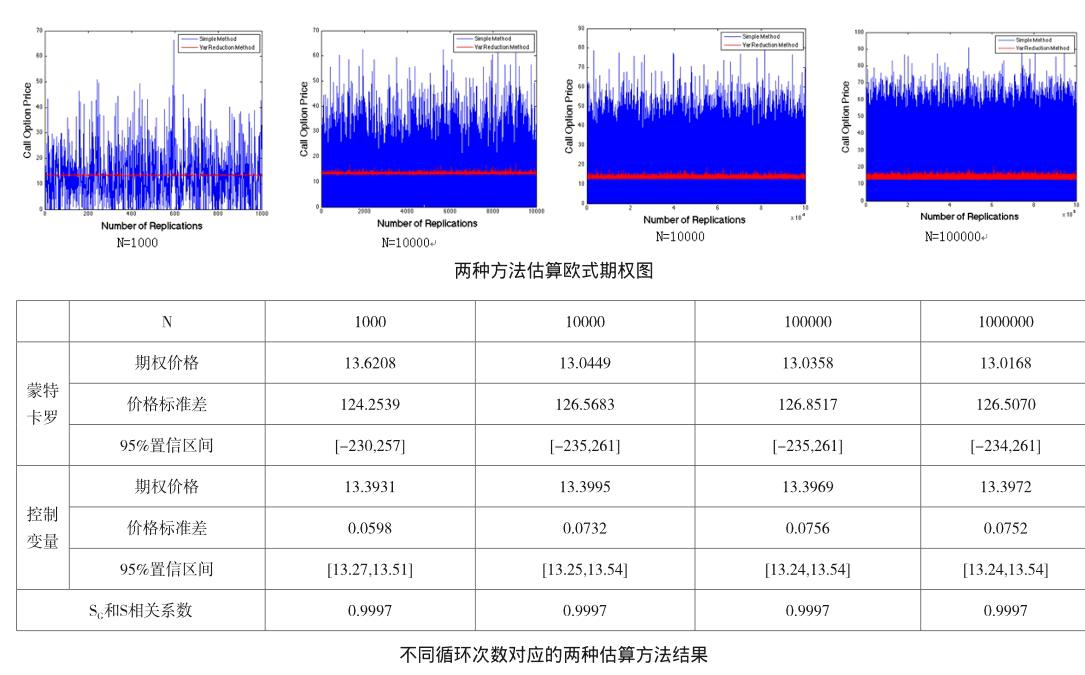
设定N为蒙特卡罗法在Matlab程序中循环的次数，分别让N=1000、10000、100000、1000000，比较经典的蒙特卡罗法和改良的蒙特卡罗法进行期权定价的过程。上面四张图分别为循环过程中得到的可能的期权价格。

上图中蓝色代表简单蒙特卡罗法估算欧式期权价格的过程，红色代表控制参数法改良后的蒙特卡罗法估算欧式期权价格的过程，可以看出前者非常不稳定，有时候价格严重偏离均值，而后者的估算精度非常高，误差很小。

根据BS模型解析式计算得到的欧式期权价格为13.3886，上表中各次试验的结果都和解析结果非常接近。但是传统蒙特卡罗法的标准差非常大，甚至达到120以上，大约是期权价格本身的10倍，如此之高的方差会损害蒙特卡罗法本身在期权定价方面的有效性，而改良后的估算法误差大大减少，并且使得置信区间变得有意义；同时，我们引入的变量SG和原有变量S的相关性极高（0.9997），也验证了上述的解析式推演结果。

四、总结

可以看出，引入的变量极大降低了估算价格的方差，使得原本无意义的置信区间具有解释期权价格的能力。因此可以说，将蒙特卡罗模拟方法与方差缩减技术结合，是提高期权定价效率的重要途径。当然，正如上文所述，方差缩减技术出控制变量外还有多种，这些方法有待于进一步研究。

参考文献：

[1] 陈辉.期权定价的蒙特卡罗模拟方差缩减技术研究.统计与信息论坛，Vol 23， No.7

[2] Lavenberg S S， Welch S S， A perspective on the use of control variables to increase the efficiency of monte carlo simulations [J]， Management Science， 1981（27）： 332-335

[3] 马俊海，张维，刘凤琴.期权定价的蒙特卡罗模拟综合性方差减少技术，管理科学学报，2005，8：68-73]

[4] Galina Galda，Variance Reduction for Asian Options， Technical report， IDE0737，2008endprint