施釉机器人灵巧度分析

黄金凤，何凯杰

（河北联合大学 机械工程学院，河北 唐山 063009）

0 引言

一般在设计机器人机械结构时，应尽量使其条件数为1，这时其灵巧性最高［1］，机构的运动学性能最好。Salibury和Craig利用雅可比矩阵J（q）的条件数作为评定Stanfo串联关节型机器人手爪理想尺度最优化的准则，雅可比矩阵J（q）的条件数越小，其灵巧性越好。本文对串联关节型陶瓷施釉机器人3种常用机构的灵巧度进行分析，选择出机器人运动性能最好的机械结构。

1 施釉机器人的3种常用机构

关节型机器人结构紧凑，易于防尘和密封，同时工作空间大，重量轻，而且工作起来比其他形式的机器人结构灵活［2－5］，适合应用在手把手示教型施釉机器人结构上。串联关节型施釉机器人3种常用结构如图1所示。

图1 串联关节型施釉机器人3种常用结构

2 机构灵巧度分析

2.1 构造机器人雅可比矩阵

对连杆坐标系的连杆参数规定如下：ai－1为从Zi－1到Zi沿Xi－1测量的距离；αi－1为从Zi－1到Zi绕Xi－1旋转的角度；di为从Xi－1到Xi沿Zi测量的距离；θi为从Xi－1到Xi绕Zi旋转的角度。

首先利用D－H法建立结构1的连杆坐标系，如图2所示。

图2 结构1连杆坐标系

结构1各连杆参数及关节变量见表1。

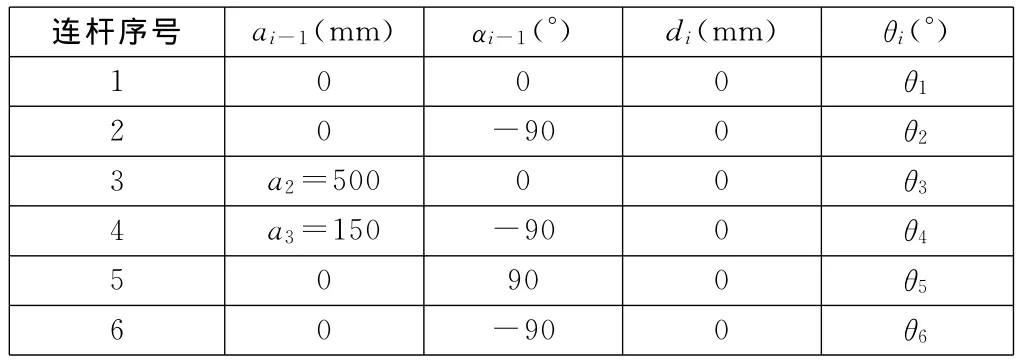
表1 施釉机器人结构1的连杆参数

连杆变换矩阵为：

其中：n为机器人自由度数。

本文用矢量积法推算出该机器人的雅可比矩阵，对于转动关节i，雅可比矩阵的第i列为：

由图2、表1和式（1）所列的连杆变换矩阵，可以计算：

（3）Z1、Z2、Z3、Z4、Z5和Z6。

（4）由式（2）和式（4）可计算1P6、2P6、3P6、4P6、5P6和6P6。

将、Zi和iP6（i＝1，2，…，6）代入式（3）得到雅可比矩阵的第i列Ji：

其中：si＝sinθi；ci＝cosθi；s23＝sin（θ2＋θ3）；c23＝cos（θ2＋θ3）。

得到结构1的雅可比矩阵J：

建立结构2的连杆坐标系如图3所示。

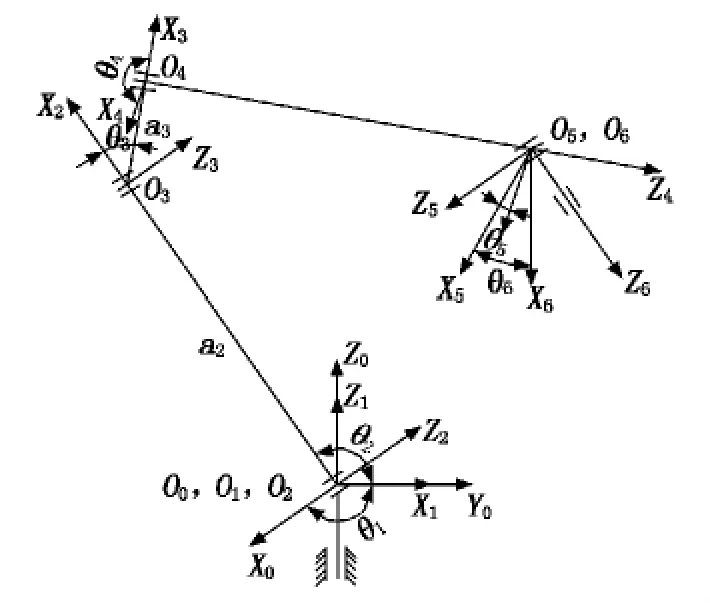
图3 结构2连杆坐标系

结构2关节数、各连杆参数及关节变量同结构1的一样，因此构造的雅可比矩阵也相同，结构2雅可比矩阵即式（11）。

建立结构3的连杆坐标系如图4所示。

图4 结构3连杆坐标系

各连杆参数及关节变量见表2。

表2 施釉机器人结构3的连杆参数

同结构1的分析过程一样，得到结构3雅可比矩阵的第i列J′i：

得到结构3的雅可比矩阵J′：

2.2 分析机器人灵巧度

由文献［1］可知条件数的定义为：

其中：‖·‖代表任意矩阵范数，通常取Euclide范数，当J（q）为满秩方阵时，J＋（q）＝J－（q），J＋（q）表示矩阵J（q）的广义逆矩阵，J－（q）表示矩阵J（q）的逆矩阵。

根据施釉机器人结构1、2和3，可知各关节工作角度范围为：θ1∈［－π/2，π/2］rad，θ2∈［0.87，2.27］rad，θ3∈［－0.7，0.7］rad，θ4∈［－π，π］rad，θ5∈［0，2π］rad。连杆参数a2＝500mm，a3＝150mm。

在角度θ的取值范围内，分别取θ1＝－1.5，－1.4，－1.3，…，1.5。以θ1为x轴，k1（J）为y轴，在MATLAB中生成的结构1和结构2的k1（J）函数图像如图5所示。

图5 结构1和结构2的k1（J）函数图象

以θ1为x轴，k2（J）为y轴，在 MATLAB中生成的结构3的k2（J）函数图像如图6所示。

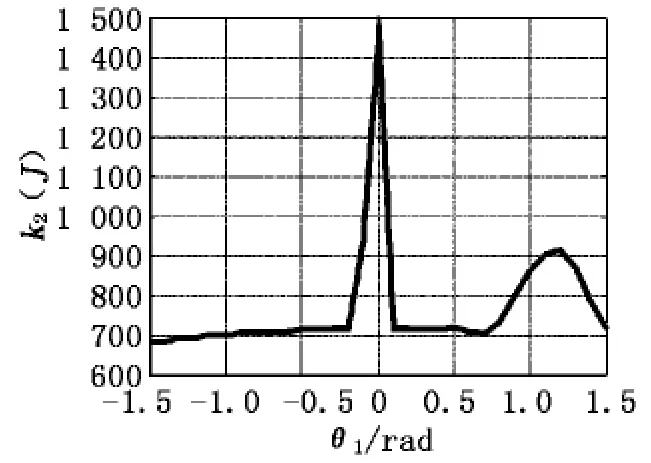
图6 结构3的k2（J）函数图象

对比图5和图6可知，常用的这3种机械结构中，结构3的灵巧性最高，运动性能最好，并且5自由度串联关节型机器人机构能够满足施釉机器人工作需要，所以结构3更适合用于手把手示教型施釉机器人的机械结构。

由图6的曲线可以看出，机器人施釉时在θ1∈［－1.5，－0.2］范围内工作最好，在此范围内对θ1、θ2、θ3、θ4进行取值，得到机器人关节的最佳工作范围，此工作范围机构灵巧度偏低，机器人最为灵活，适合手把手示教。

3 结论

本文提出了3种手把手示教型串联关节施釉机器人结构，通过对结构进行的运动学分析，分别构造出机器人的雅可比矩阵，分析得出了3种机器人的灵巧度，得到最优的手把手示教型串联关节施釉机器人的机械结构。

［1］熊有伦.机器人学［M］.北京：机械工业出版社，1993.

［2］李晨辉.手把手示教型施釉机器人关键技术研究［D］.唐山：河北联合大学，2010：15－22.

［3］张焕.六自由度机器人结构设计、运动学分析及仿真［D］.西安：西安理工大学，2004：6－12.

［4］殷际英，何广平.关节型机器人［M］.北京：化学工业出版社，2003.

［5］张进伟.四自由度平面关节型机器人结构分析与优化［D］.沈阳：东北大学，2008：4－17.