基于MATLAB的曲面施釉轨迹优化仿真

张丽梅，霍 平

(华北理工大学 机械工程学院，河北 唐山 063210)

0 引言

施釉机器人在陶瓷卫浴行业的应用，极大地提高了陶瓷卫浴的生产效率。随着人们对陶瓷釉面质量要求的提高，工厂对施釉机器人性能的要求也越来越高[1]。高效率、高品质和智能化是当今施釉机器人的发展趋势，对机器人施釉轨迹进行优化是提高陶瓷釉面质量的主要手段。改进原有的施釉机器人轨迹优化理论，在施釉机器人轨迹优化研究领域具有很大的现实意义。本文根据工件模型上各点的法矢信息确定喷枪角度，在假定喷涂高度和喷枪走速恒定的前提下，对施釉路径进行规划，并通过MATLAB程序进行优化仿真，验证了轨迹优化方法的正确性。

1 施釉曲面数据采集与处理

由于实际生产的施釉环境复杂且存在一定的危险性，本研究对机器人曲面施釉轨迹优化的过程进行了仿真实验，曲面施釉轨迹优化仿真的MATLAB程序由曲面数据录入和处理程序、曲面涂面厚度计算程序、曲面喷涂效果显示程序等几个部分组成，如图1所示。

图1 MATLAB优化仿真程序组成框图

本研究采用的FARO QUANTUMS FAROARM激光扫描仪有激光扫描和点接触采集两种数据采集方式[2]，此扫描仪在数据获取方面有较大的优势，经测量仪测得的曲面数据是一系列的三维点云。以图2所示的工件实物模型为研究对象，对曲面工件使用三坐标测量仪进行模型的点云数据采集，测量过程如图3所示。

图2 曲面工件实物模型 图3 曲面点云数据采集

经测量所得部分点云数据如表1所示。

表1 部分点云数据

为得到质量更好的工件表面模型，需要对扫描所得的曲面点云数据进行预处理[3]，这里截取了一部分点云数据进行研究，截取的原始点云数据如图4所示。

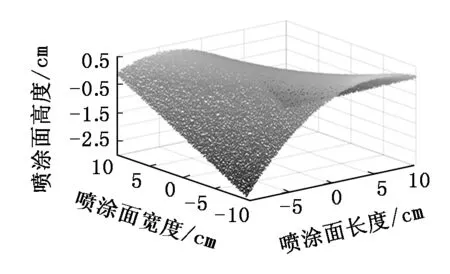
图4 原始点云数据

由图4可以看出，此时的点云数据光滑度比较低，有比较明显的偏离点，因此需要进行点云去噪处理，这里采用了最小二乘法进行去噪，具体步骤如下：

(1) 首先计算出最大连通域，查得三维点云在X、Y、Z轴上的最大值，找出平行于各坐标轴的最小数据集，确定栅格边长Ls=0.5 cm。

(2) 采用最小二乘法拟合曲面。

(3) 采用去噪策略进行噪声点的去除，其中计算每个点到曲面的距离的MATLAB程序为：

D=abs(a*p(1)+b*p(2)+c*p(3)+d)/sprt(a^2+b^2+c^2)

程序中a、b、c、d为面的一般形式ax+by+cz+d=0的各项系数，p(1)、p(2)、p(3)表示曲面上任一点在X、Y、Z方向上的坐标。

判断各点是否为离群点，对离群点进行去除，去噪后的效果如图5所示。

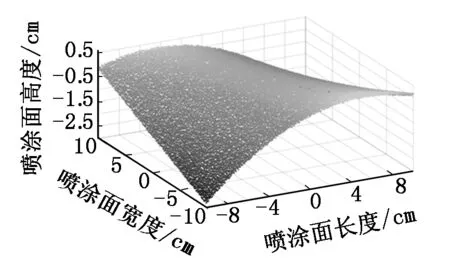
图5 点云数据去噪后的效果

与原始点云数据相比，去噪后的效果图中点云分布已经比较平滑整齐了，这里可以省略点云平滑等相关操作，但从图中可以看出，此时的点云密度仍然较大，需要进行精简。点云数据精简的实质是挑选出适量具有代表性的、能够完整地展现曲面特征的特征点。精简后的效果如图6所示，表面光滑平整、没有离散点的存在且数据量适中。

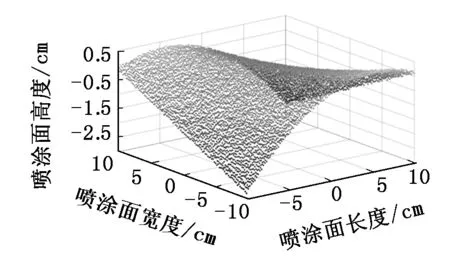
图6 点云数据精简后的效果

对精简后的点云图进一步拟合可得到如图7所示的效果，可直接用于MATLAB仿真。

图7 点云数据拟合效果

2 曲面施釉轨迹优化仿真

2.1 验证施釉模型正确性

将工件实物模型平放，分成上表面和下表面两部分，上表面的形状较为复杂，曲率变化较大。以上表面为重点研究对象制定施釉方案，进行施釉仿真分析，能更准确地验证优化方法的优越性，定向施釉方案如图8所示。对工件的上表面进行定向的施釉仿真，即保持喷枪的喷涂方向不变进行施釉，在进行施釉轨迹的优化之前，可以人为给定喷枪一条路径进行施釉，这可以认为是施釉路径的规划阶段[4-5]。

如图9所示，喷枪沿一条施釉路径由位置1到位置n进行施釉仿真，设定喷枪的移动速度，由于上表面的高度远大于单条施釉路径在竖直方向上的喷涂范围，所以需要按照以上路径进行多次施釉。这里设各路径在竖直方向的间距D=80 mm，将施釉轨迹录入MATLAB进行施釉仿真，得到如图10所示的施釉效果。

图8 定向施釉方案 图9 定向施釉路径

由先前的研究可知，釉层厚度的分布以喷枪中心向边缘逐渐减小[6]，图10中颜色越浅表示釉层厚度越大，如图10所示的a区域颜色较浅，厚度较大，b区域颜色较深，厚度较小。图11为上表面釉层厚度分布示意图，上方的曲线代表工件的上表面，下方曲线代表釉层表面，两条曲线之间为釉层厚度。在进行定向施釉时，喷枪保持移动方向和角度不变，在喷头与工件距离较远处，釉层分布较薄；在喷头与工件距离较近处，釉层分布较厚，在曲率较大的部分，釉层厚度分布变化明显，符合客观事实，验证了涂层累积速率模型和涂层厚度模型的正确性。

图10 定向施釉效果 图11 上表面釉层厚度分布

2.2 曲面轨迹优化仿真

喷枪轨迹的确定以工件表面的点为基准[7]，理想的喷枪路径是喷头与工件表面的点以一定的距离一一对应，但是工件表面存在大量的数据，计算量巨大，所以这里采用分片的方式简化工件表面的点，即将工件表面一个较小区域中的点集简化成一个面片，将工件的大曲面看成是由多个小曲面组成，各个小曲面的法矢方向即为喷枪的方向，各小曲面的中心点即为喷枪喷头对应的点，如图12所示。

设置喷枪与工件表面的距离h=120 mm，喷枪移动速度为v=300 mm/s，按照给定的施釉路径方案进行仿真研究，如图13所示为其中一条优化后的施釉路径，每个箭头的位置代表喷枪的位置，规定喷枪沿从位置1到位置2再到位置n的方向移动，这里与定向施釉时一样设各路径在竖直方向的间距D=80 mm，且其他路径均平行于第一条路径。

按照上述轨迹规划方案利用MATLAB进行施釉仿真，整体的施釉釉层厚度仿真效果如图14所示。

如图15所示为放大后的釉层厚度分布曲线，内侧曲线代表工件表面，外侧曲线代表釉层表面。从图15中可以看出：共有两处区域的涂层厚度变化较大，这是由于这两处曲率变化较大、喷枪的方向发生较大幅度的改变引起的。仿真结果符合预期，证明了研究过程的正确性。

图12 喷枪喷头与工件表面对应关系 图13 优化后的施釉路径

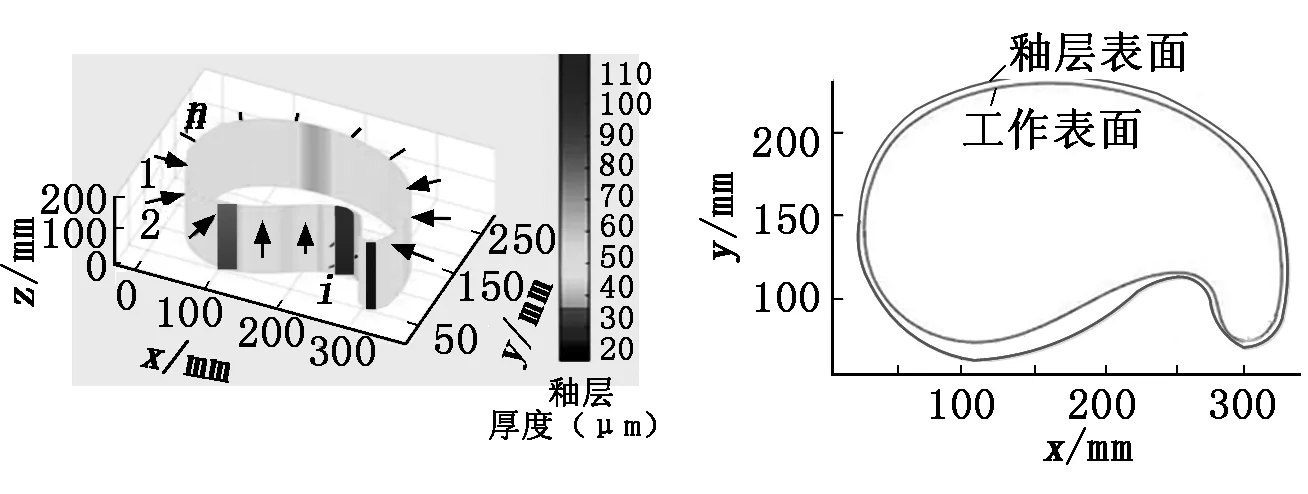
图14 釉层厚度仿真效果 图15 水平截面釉层厚度

3 总结

对施釉机器人进行轨迹优化，是获得厚度均匀分布的釉层和减少釉料用量的关键，如何提高施釉效率，将一直是值得深入研究的问题。本文以有明显曲率变化的实体为研究对象，在给定施釉路径的前提下，进行关于复杂曲面的施釉轨迹优化仿真。本文关于点云数据的理论研究和处理为后续的研究奠定了理论和技术基础。通过MATLAB程序进行轨迹优化仿真，结果验证了优化方法的正确性，具有一定的现实意义。