线控换档开关中的凸轮机构研究

张志强，陈辛波，岳 彪

（同济大学 汽车学院，上海 200237）

0 引言

汽车线控技术就是将驾驶员的操纵动作经过传感器变成电信号，通过电缆直接传输到执行机构的一种系统［1］。目前的线控技术包括线控换档系统（Shift－By－Wire）和线控制动系统（Brake－By－Wire）、线控转向系统（Steering－By－Wire）等等［2］。

本文研究的是线控换档开关，凸轮机构是其核心组成部分，对开关功能设计的实现起着关键性作用。

1 线控换档开关凸轮机构设计与分析

1.1 线控换档开关凸轮机构选型

研究换档开关内部的凸轮机构，重点是要研究在操作开关过程中，凸轮机构对开关使用者力和行程的反馈［3－4］。图1为开关内部凸轮机构示意图。

图1 线控换档开关内部的凸轮机构

1.2 旋转角度与旋转力矩的数学模型

凸轮曲面对弹簧顶销的作用力FN可分解为压缩弹簧产生的弹簧力FF和旋转方向的切向力Fφ，如图2所示。图2中，α为力分解角度。

弹力FF与位移x的关系为：

其中：c为弹簧的弹性系数；x为弹簧的压缩变形量。x又代表了凸轮曲面的轮廓与旋转角度的关系，于是有FF（φ）＝cx（φ）。

图2 力分解示意图

凸轮曲面对弹簧顶销在旋转方向的分力产生恢复力矩Mφ（φ），曲面与弹簧顶销的接触点到转轴中心的距离r（φ）为恢复力臂［5］，因此有：

在凸轮曲面任意点的弹簧力FF和旋转方向切向力Fφ之间的关系如图3所示，此点的斜率为Δx/Δφ［6］，有：

对无穷小的区域求导，则有：

可以得出轮廓方程与切向力Fφ的关系式为：

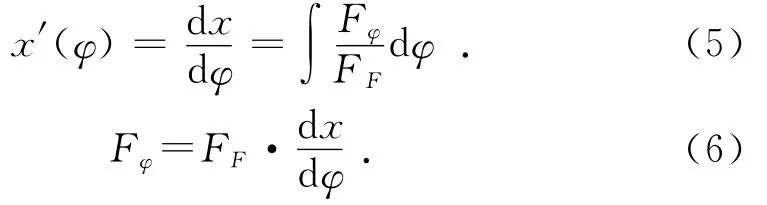
联立式（5）与式（6），则有：

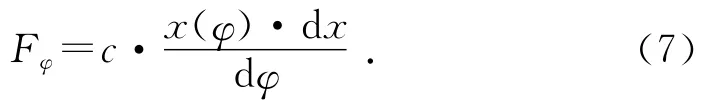
设想当弹簧力不受弹簧压缩变形量x和旋转角度φ的影响，FF为定值FF0，则可以得出理想化的恢复力矩Mφ与凸轮曲线方程x（φ）之间的关系式［7］：

由于l为弧长，r为半径，则有l＝rφ，则：

联立方程（7）与方程（9）可以得出半径r与恢复力矩Mφ的关系式为：

最终得到曲线方程与回复力矩的关系式为：

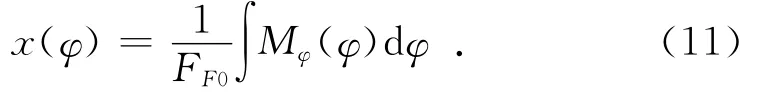
图3 弹簧力FF和切向力Fφ的关系

2 CATIA三维建模和SimDesiger仿真计算研究［8］

2.1 凸轮曲面的三维建模

在线控开关中，凸轮曲面结构集成在开关壳体结构中固定不动，当旋钮转动时，旋钮上的转轴带动弹簧顶销转动，转轴的中心也是凸轮基圆的圆心，吕轮机构如图4所示。

图4 换档开关内部的凸轮机构图

2.2 凸轮机构运动仿真

在CAITIA中选择SD Motion Workbench模块，可以直接进入SimDesiger环境，对当前的CATIA数据进行力学及运动仿真［9］。凸轮机构仿真工作流程如图5所示。

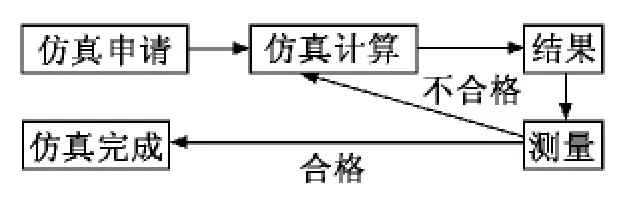
图5 运动仿真工作流程图

当测量结果与计算结果不符时，需要对各参数的设置重新进行复核，找到造成差异的根本原因，重新进行计算。

3 开关操作手感测试

经过三个月的模具加工制造和样品试装之后，我们拿到了线控换档开关的样机。理想状态下，旋转类开关的力行程曲线如图6所示。图6中，φ2为旋转档位旋转扭矩最大值对应的旋转角度值；φ1＝φ2－7.5°；φ3＝φ2＋7.5°。

图6 旋转类开关力行程理想曲线

在工程应用中，常用参数SR1及SR2来评判旋转类开关的操作手感。SR1、SR2定义如下：

其中：M2为旋转档位旋转扭矩最大值；M1为旋转角度为φ1时对应的旋转扭矩值；M3为旋转角度为φ3时对应的旋转扭矩值。

在实际生产应用中，通常SR1及SR2在20%～40%范围内，表明开关操作手感良好。经高温处理后，开关测试及计算结果如表1所示。

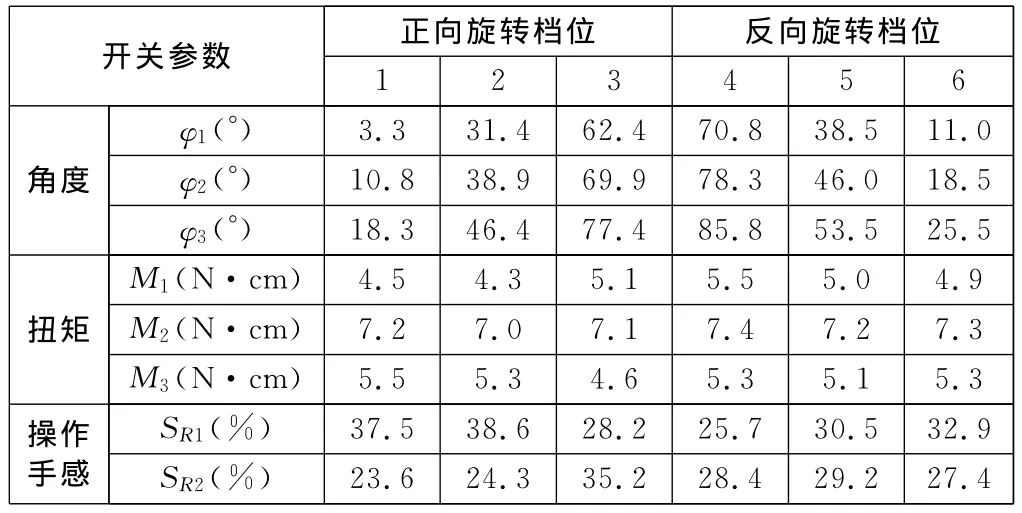
表1 线控换档开关高温处理后参数统计表

采用相同方法，依次计算高低温后、耐久后、振动后的SR1和SR2值。经计算，得到的结果均在20%～40%范围内。表明线控换档开关在高温后、低温后、耐久后、振动后，操作手感良好，符合操作手感要求。

4 总结

本论文主要研究空间凸轮机构在汽车线控换档开关中的开发及应用，主要研究成果如下：

（1）对凸轮机构的组成、应用、运动规律、凸轮机构的选型及凸轮机构的力行程曲线理论进行了阐述。

（2）应用CATIA三维建模软件对线控换档开关中的核心机械机构——凸轮曲面机构块进行了三维软件模拟，并应用SimDesige仿真计算软件进行了仿真计算验证。

（3）对实物样件展开实验分析。定义了旋转类开关手感评判参数SR1及SR2，并对其在高温后、低温后、耐久后、振动后进行了测试，绘制了力行程测量曲线。测量结果表明线控换档开关手感良好，满足操作手感要求，技术指标满足客户要求。

［1］贺炜，曹巨江，杨芙莲，等.我国凸轮机构研究的回顾与展望［J］.机械工程学报，2005（6）：1－6.

［2］Fu Yan－ming.Analysis and design of the globoidal indexing cam mechanism ［J］.Journal of Shanghai University（English Edition），2000，4（1）：54－59.

［3］何仁，李强.汽车线控转向技术的现状与发展趋势［J］.交通运输工程学报，2005（2）：68－72.

［4］管荣法.凸轮与凸轮机构［M］.北京：国防工业出版社，1991.

［5］郑晨升，葛正浩.凸轮机构从动件运动规律的通用表达式［J］.机械科学与技术，1996，15（1）：151－155.

［6］Fan Y Chen.凸轮机构动力学模型的建立方法［J］.机械设计与研究，1987（4）：43－52.

［7］Jong－Soo，Kho－Eop Yoon.Design of traverse cam for yarn winding on twisting machine［J］.Fibers and Polymers，2005，6（2）：151－155.

［8］林永.CATIA 在 CAD/CAE/CAM 行业的应用［M］.北京：北京科技大学出版社，2000.

［9］Hans G rabowski， Reiner Anderl， Michael J Pratt.Advanced modelling for CAD/CAM systems［J］.Research Reports ESPRIT，1991，7（1）：21－22.