基于ANSYS Workbench 14.5的某客车架结构模态分析❋

2015-12-31窦宝华戴作强张铁柱

机械工程与自动化 2015年3期

窦宝华，戴作强，张铁柱，盛建

（1.上海申沃客车有限公司，上海 201108；2.青岛大学，山东青岛 266001）

0 引言

汽车车架是汽车最为重要的承载基体，一方面，它连接着汽车的各大总成，使其各总成保持相对正确的位置；另一方面，它承受着汽车行驶过程中遇到的各种形式的复杂载荷。因此，汽车车架的结构性能在很大程度上决定了车辆整体质量的好坏。汽车在行驶的过程中，在不平路面、不断变化的运动方向和车速以及不平衡的传动系统等激振的共同作用下，整车及车辆局部会产生强烈振动。当上述激振频率与车架本身的固有频率大小相接近时，共振现象就会发生［1］。对于汽车来讲，共振现象的危害性是非常巨大的，长时间的共振不仅影响车辆的乘坐舒适性，还极易造成车架结构变形、疲劳破坏，进而导致车辆使用寿命的大幅度缩短及安全性能的大幅度降低。

针对上述问题，本文对某客车车架进行了相应的模态分析，进一步确定了车架各阶振型及其对应的各阶固有频率等动力特性参数。车架的这些动力参数的确定对汽车车架的结构设计及优化极为重要。

1 模态分析理论基础

模态指的是多自由度系统在以一定固有频率振动时所表现出来的振动形态。此时，多自由度结构上的每个点相对于平衡位置的位移之间具有一定的比例关系，结构上每个点对外力的响应均可表示为结构的各阶模态阵型的线性叠加。模态分析的最终目标就是识别出系统的模态参数，为结构系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据。设计人员利用所得分析结果得到产品结构对不同类型的动力载荷的响应规律，有助于其在其他动力分析中估算求解控制参数［2］。

无阻尼模态分析是经典的特征值问题，其动力学运动方程为：

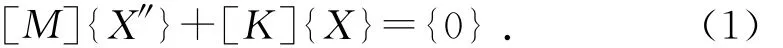
其中：［M］、［K］分别为结构的质量矩阵、刚度矩阵；｛X｝、｛X″｝分别为系统节点的位移矢量和加速度矢量［3］。式（1）的解的基本形式为：

代入式（1）得：

由式（3）求得方程的特征值ω2。根据ωi＝2πfi即可求得结构的对应固有频率，即模态频率fi。特征值ω2i对应的特征向量｛Xo｝i即为模态频率fi对应的结构模态振型。

2 车架模态分析计算

本文所研究车架采用全承载边梁式结构，通过螺栓连接将其前、中、后三段总成组合成为车架，其横梁、纵梁均采用槽钢。车架总长为9 950mm，总宽为850 mm，槽钢厚度均为7mm，总质量为950.6kg。

本文研究思路为首先在SolidWorks中建立车架的三维实体模型，并将其保存为x＿t格式以便导入到ANSYS Workbench 14.5进行后续的有限元分析。为了更加快捷高效地对车架进行模态分析，我们应适当对车架进行简化处理，将不必要的零件及小孔去掉。最终建立的车架三维实体模型如图1所示。

图1 车架三维实体模型

在ANSYS Workbench 14.5中对导入的模型进行材料参数的设定。本车架采用的材料为Q345，其具体材料参数如表1所示。

表1 车架材料参数

对定义完材料属性的车架进行网格划分。车架网格划分的原则是“均匀应力区粗化，应力梯度区细化”。本文主要采用六面体网格划分方法对车架进行网格划分，网格划分后的车架有限元模型如图2所示。

对车架的有限元模型进行网格划分后，对其施加载荷和边界条件。由于我们研究的是车架的自然频率、振型以及振型参与系数，因此本文在模态分析中不需对车架施加载荷，只需对车架设置固定约束Fixed Support即可。为了更加真实地求得车架的动态参数，固定约束施加位置为车架的主要支撑点。

图2 车架有限元模型

车架有限元模型的边界条件建立完成后，需要设置合适的求解频率选项以便得到理想的求解结果。众所周知，模态分析研究的是结构的振动性能，即结构的各阶固有振型及其各阶固有频率等动态特性参数，所研究对象的振动实际上是其各阶固有振型的线性组合［4］。相关实验表明，车架的低阶振型对其振动动态性能所产生的影响相对其高阶振型更加显著，所以车架的动态性能主要取决于低阶振型。故我们仅需将Analysis settings中的Max Modes to find设置为6，即只求解车架的前6阶振型即可。设置完成后，利用ANSYS Workbench中的Solve求解，即可得到车架的前6阶固有频率和振型。经过计算求解得到车架前6阶固有频率（Hz）分别为14.875、35.662、36.73、44.247、46.173和48.094。车架的前6阶振型如图3～图8所示。

图3 车架第1阶振型（14.875Hz）

图4 车架第2阶振型（35.662Hz）

图5 车架第3阶振型（36.73Hz）

图6 车架第4阶振型（44.247Hz）

图7 车架第5阶振型（46.173Hz）

图8 车架第6阶振型（48.094Hz）

根据该车架的模态分析结果可知：该车第1、2阶振型所对应的车架变形以车架后部的上下摆动为主；第3阶振型所对应的车架变形以车架前部弯曲变形为主；第4阶振型所对应的车架变形以车架后部侧向扭转变形为主；第5阶振型所对应的车架变形以车架中部摆动变形为主；第6阶振型所对应的车架变形以车架后部侧向弯曲变形为主。

3 模态分析结果评价

虽然现在行业内对模态分析结果还没有一个比较一致的评价标准，但目前主要有两大类，即类比判断与分析判断［5］。类比判断法就是用在实践检验中表现良好的同类型车架的模态性能来作参照比较；分析评价法则把由外界激励频率以及在此频率下的激励分量值和研究对象自身的固有频率及其对应振型所组成的动态响应作为评判标准［6］。本文采用分析评价法对模态分析结果进行评价。

电动汽车的激励主要是路面激励和传动轴激励，了解上述激励的组成是模态分析的前提，各种激励的频率分析如下：①路面激励主要取决于路面状况，对于客车经常行驶的一般城市路面以及高速公路来讲，其对应的路面激励频率一般在1Hz～3Hz之间；②根据相关规定，城市中的车速一般是在40km/h～80km/h之间，而高速公路的车速大多是90km/h。在这种车速的情况下，客车传动轴的激励频率一般大于30Hz。

通过前面分析可知，车架的第1阶模态频率为14.875Hz，其大于路面激励频率，同时又小于传动轴激振频率，因此车架不会出现共振现象。后5阶模态频率值都大于30Hz且与传动轴的激励频率相接近，车架可能会发生共振。但是传动轴激励频率值较广，如果车速发生改变，传动轴激励频率值也会相应地改变，所以车架出现共振的概率不大。再者，就算出现共振现象也是高频振动，构成的破坏也是不大的。因此本车架基本满足设计要求。