机器人动力学模型在轨迹规划中的应用

白云飞

（运城学院 机电系，山西 运城 044000）

0 引言

机器人动力学模型反映了关节力矩（力）与关节变量、速度、加速度之间的函数关系，其重要作用是：①可用来开发合适的控制策略，要想获得期望的运动轨迹，某些控制方案可直接依靠动力学模型来计算需要驱动器施加的力矩和力；②用来实现机器人系统的计算机模拟，通过检查在不同操作条件下模型的行为，可以预测出当机器人系统被建立起来以后机器人会如何运动；③可提供所有的关节作用力和力矩，这些是设计和选择连杆、支座、驱动器的主要依据［1］。

本文应用拉格朗日方程建立单自由度机器人的动力学模型，规划机器人常用的3种运动轨迹，并运用MATLAB软件进行逆动力学仿真，以验证所规划轨迹的正确性。

1 拉格朗日方程［2］

N自由度串行机器人的拉格朗日函数L可以表示为：

其中：EK为系统总动能；EP为系统总势能。

若第i个关节是线性关节，则N自由度串行机器人的拉格朗日方程可以表示为：

其中：xi为位移；Fi为作用在第i个关节上的驱动力。

若第i个关节是转动关节，则N自由度串行机器人的拉格朗日方程可以表示为：

其中：θi为角位移；τi为作用在第i个关节上的驱动力矩。

2 单自由度机器人动力学模型

图1为单自由度机器人示意图，根据拉格朗日方程建立其动力学模型。

系统总动能为：

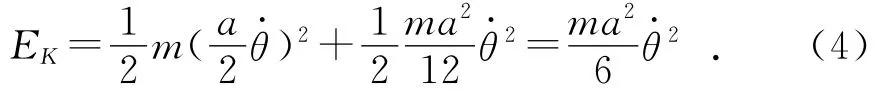
其中：m为单自由度机器人的质量；a为机械臂长度。

图1 单自由度机器人

由式（4）、式（5）可得单自由度机器人的拉格朗日函数L为：

系统总势能为：

把式（6）代入式（3），则作用在机器人关节上的力矩τ为：

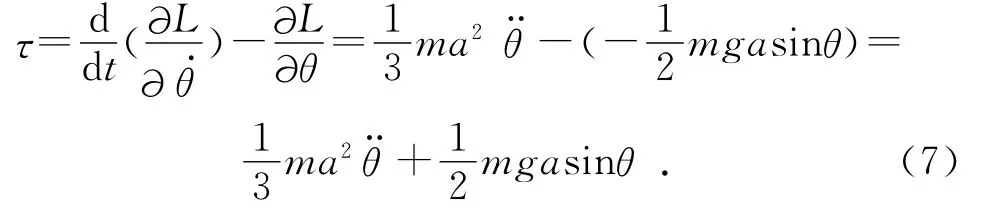
3 使用MATLAB软件进行轨迹控制

轨迹规划是指根据作业任务要求（作业规划），关于末端执行器在工作流程中位姿变化的路径、取向以及它们的变化速度和加速度的人为设定，它是运动学反解（位姿和速度、加速度的反解）的实际应用［3］。以下对单自由度机器人常用的3种运动轨迹进行规划。

3.1 抛物线过渡的线性轨迹规划

在抛物线过渡的线性轨迹规划中，单自由度机器人关节的角位移θ（t）为：

其中：θ0为起始关节角度；θf为终止关节角度；为抛物线段的加速度；tf为机器人从起始点到终止点的运行时间；tc为抛物线段持续的时间。

角速度θ·（t）为：

角加速度（t）为：

抛物线段持续的时间tc［4］为：

取θ0＝30°，θf＝70°，tf＝5s，＝10°/s，采用抛物线过渡的线性轨迹规划单自由度机器人的运动轨迹。由式（11）计算得tc＝1s。取a＝1m，m＝1kg，用MATLAB进行仿真，结果如图2所示。

由图2可以看出，采用抛物线过渡的线性规划方法，位移曲线平滑，速度曲线连续，加速度无突变，机器人作业时运动平稳，冲击小，对驱动器输出力矩的控制比较容易实现。

图2 抛物线过渡的关节曲线运动

3.2 多约束轨迹规划

在角位移、角速度和角加速度都有约束的多约束轨迹规划中，单自由度机器人关节的角位移θ（t）为：

其中：T为正弦函数的周期。

关节角速度（t）为：

关节角加速度（t）为：

图3 多约束轨迹规划的关节曲线

从图3看出，采用多约束轨迹规划方法，位移曲线平滑，速度曲线和加速度连续，机器人作业时运动平稳，冲击小，对驱动器的控制容易实现，综合性能好。

3.3 三次多项式轨迹规划

用三次多项式进行轨迹规划时，单自由度机器人关节的角位移θ（t）为：

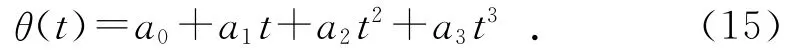
其中：a0、a1、a2和a3均为待定系数。

关节角速度（t）为：

关节角加速度（t）为：

取θ0＝0°，θf＝90°，tf＝2s（0）＝（tf）＝0，使用三次多项式规划单自由度机器人的运动轨迹，确定的轨迹方程为：

取a＝1m，m＝1kg，用MATLAB仿真的结果如图4所示。

图4 三次多项式轨迹规划关节曲线

从图4看出，采用三次多项式轨迹规划方法，位移曲线平滑，速度曲线和加速度曲线连续，机器人作业时运动平稳，冲击小，对驱动器的控制容易实现。

4 结论

拉格朗日方程作为一种分析力学方法，是建立机器人动力学模型的有效方法。根据期望的运动轨迹，利用机器人动力学模型，能够实现机器人的动态控制，完成不同的作业任务。

［1］S K SAHA.Introduction to Robotics［M］.北京：机械工业出版社，2009.

［2］刘极峰.机器人技术基础［M］.北京：高等教育出版社，2006.

［3］韩军，郝立.机器人关节空间的轨迹规划及仿真［J］.南京理工大学学报，2000（6）：540－543.

［4］Saeed B Niku.机器人学导论——分析、系统及应用［M］.孙富春，译.北京：电子工业出版社，2004.