一种计算复合材料湿扩散系数的等参化FVDAM模型
2015-12-31李海斌阳建红刘承武
李海斌,阳建红,张 晖,刘承武
(1.第二炮兵工程学院,陕西 西安 710025;2.中国人民解放军96215部队,广西 柳州 545616)
0 引言
聚合基复合材料普遍具吸湿特性。湿扩散系数是衡量湿扩散速度的重要参数,一般可由实验获得,但实验周期较长。复合材料的性能与各相材料的性能密切相关,采用细观力学方法,可由各相材料性能获得复合材料的整体性能,如热-机械性能、湿-热-弹性能和湿扩散性能等。针对湿扩散,文献[1-2]采用类比热传导、电流传导的方法,对横向湿扩散系数进行推导。其中,SHEN,SPRINGER主要针对纤维不吸湿性质,且认为纤维对水分扩散有阻碍作用,水分沿直线扩散,导致计算结果小于实验值;HASHIN获得半经验公式,计算结果依赖于拟合参数;PIGGOTT考虑纤维与基体间存在界面相并认为界面相的扩散系数大于基体,显然在确定界面层厚度及界面层扩散系数时存在随意性。另外,上述模型的共同不足是只能考虑特定截面形状的微结构。采用数值方法可对不同微结构形状的复合材料进行计算。文献[3-4]用有限元方法分析了编织复合材料的湿扩散行为;文献[5]则考虑纤维的随机分布,对复合材料扩散过程进行数值模拟。但这些研究仍针对纤维不吸湿情形。对吸湿的情形(如芳纶),复合材料横向扩散系数的求解需考虑纤维自身的吸湿。
文献[6-7]提出的单胞模型已成功用于复合材料宏观性能的计算及细观应力/应变场的求解,模型位移模式已从一阶扩展至二阶,具有较高精度;文献[8]在模型中引入有限体积的求解;文献[9-10]则采用网格映射方法,实现网格划分从矩形向任意四边形的转变,建立了等参化FVDAM。本文将该模型推广至复合材料湿扩散系数的求解,使其适于纤维自身吸湿情形,并将其用于分析芳纶复合材料吸湿行为。
1 湿扩散的等参化FVDAM模型
在等参化FVDAM计算机械性能中,对微结构进行网格划分后,假设单元内的位移模式,用等参变换、网格映射方法,以及界面位移、应力的连续条件和单胞内的平衡方程求解。在稳态湿扩散时,同样可假设单元内的浓度场函数,用界面相对湿浓度连续、湿流通量连续,以及扩散的质量守恒方程求解。湿扩散的单胞模型如图1所示。模型被划分为Nβ×Nγ个子胞单元,每个单元用(β,γ)标记。图中:F1~F4为各面序号。

图1 湿扩散的单胞模型Fig.1 Method of cells for water diffusion
在映射坐标系(η,ξ)内,设
a)单胞中的相对浓度场

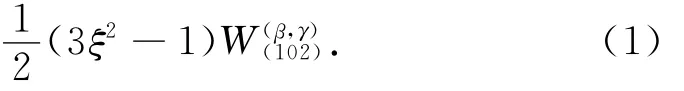
b)扩散方程
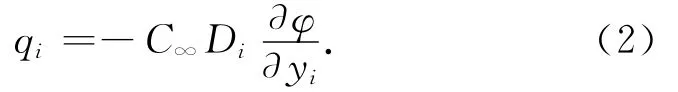
式中:qi为湿流通量;Di为湿扩散系数;i=2,3。
c)稳态扩散的质量守恒方程

φ(β,γ)对坐标的一阶和二阶偏导数在坐标系(y2,y3),(η,ξ)中存在转换关系(为简化表达,以下公式均省略上标)

式中:J为雅克比转换阵;为J在单胞内的体积平均。
定义界面平均湿浓度

式中:上标表示面序号,按逆时针方向选取,由式(5)、(6)可将一阶和二阶微变量用界面平均湿浓度及零阶微变量表示为
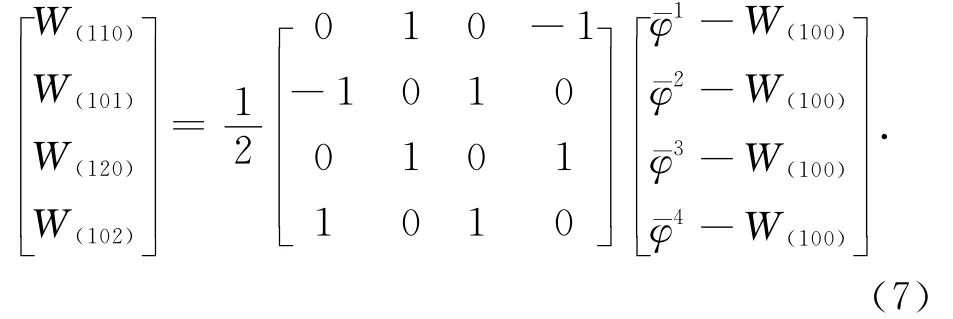
零阶位移微变量可由满足能量守恒方程式(3)求得,用扩散方程式(2)得

用湿浓度对坐标二阶偏导数的转换关系式(5)表示一阶微变量用界面平均湿浓度,进而通过式(7)将一阶和二阶微变量同样用界面平均湿浓度表示为

定义界面平均湿浓度梯度

界面平均湿流通量

用扩散方程式(2),湿流通量用湿浓度梯度可表示为

式中:n2,n3为法向量。对各面分别有

由式(9)、(14),可表示为相对湿浓度的关系式

式中:K为连接湿流通量与的转换矩阵,包含了各单元的几何结构信息,且与各单元的法向量及湿扩散系数有关。
在相邻子胞上,界面上相度湿浓度和湿流通量连续可表示为
a)当β=Nβ时,β+1→1,

湿浓度的边界条件为

式中:β=1,…,Nβ-1。
由式(15)~(19),可对水平方向宏观扩散系数Dc3进行求解,有

式中:符号“〈〉“表示在单胞内求体积平均;Cc∞为复合材料的吸湿平衡浓度,且Cc∞=Cf∞Vf+Cm∞(1-Vf)。此处:Cf∞,Cm∞分别为纤维和基体的平衡吸湿扩散含量;Vf为纤维体积分数。
在稳态热传导中,因热传导同样在界面存在温度连续、热流密度连续条件,同时满足热传导方程和质量守恒方程,故在上述推导中将有关湿扩散的性能参数替换为与热传导相关的性能参数即可求得宏观热传导系数。
2 湿扩散系数求解
为便于比较,本文给出纤维不吸湿(即纤维扩散系数Df=0)时,不同纤维体积的归一化横向扩散系数如图2所示。本文计算结果介于Shen-Springer,Piggott公式间,且与Hashin公式在低体积含量时的结果吻合较好,仅在高体积含量时产生偏差。文献表明:由Shen-Springer公式得到的结果普遍较实验值偏小,这是因为Shen-Springer在推导公式时,认为水分沿直线扩散,纤维不仅不吸湿,对水分扩散还有阻碍作用,而Piggott公式结果稍高,这是因为其考虑纤维与基体间存在界面相,且界面相的扩散系数远高于基体[2]。由图2可知:体积含量相同时,方形纤维与圆形纤维的扩散系数相差较大。为较准确地求解扩散系数,模型须准确反映纤维的截面形状。等参化FVDAM采用四边形进行网格划分,能对复杂代表性胞元(RUC)进行建模,满足此要求。

图2 不同纤维含量的横向扩散系数Fig.2 Transverse diffusion coefficient under various fiber contents
材料湿扩散性能为横观各向同性。在图1(a)的边 界 条 件 下,不 吸 湿 纤 维 (Df/Dm=0.1,Cf∞/Cm∞=0.1)和吸湿纤维(Df/Dm=10,Cf∞/Cm∞=10)RUC内的湿流通量y2,y3分布如图3所示。此处:Dm为基体扩散系数。由图可知:纤维不吸湿时,其内部的湿流通量很小,水分主要在基体中传播,但水分能沿纤维周向扩散,而非Shen-Springer模型中的直线扩散,因而求得的复合材料等效横向扩散系数高于Shen-Springer公式值;纤维吸湿时,其内部的湿流通量更大,更能反映纤维自身具有吸湿性的复合材料如芳纶复合材料的吸湿特征。

图3 湿流通量分布Fig.3 Moisture flux in cell
3 复合材料吸湿实验
在温度分别为60,80℃,相对湿度均为90%的条件下,对Vf=60%的芳纶APMOC、环氧基体Epoxy,以及由两者组成的芳纶复合材料进行吸湿实验,一定时间将试件取出用滤纸除去表面水分,在电子天平称重计算吸湿前后质量变化百分比。芳纶复合材料吸湿表现为各向异性扩散行为[11]。用于复合材料吸湿实验的单向板试件有3种,尺寸见表1。

表1 用于吸湿行为分析的单向板尺寸Tab.1 Laminates of different size
纤维、基体,以及芳纶复合材料的吸湿曲线如图4所示。由图可知:三者吸湿行为基本符合扩散方程式(2),在吸湿初期均呈线性上升趋势,之后逐渐进入吸湿平台,最终达到吸湿平衡,但由于结构不同,三者的吸湿行为仍显示不同特征。其中:芳纶APMOC在10d内很快进入吸湿平台,其平衡吸湿量约5%;Epoxy在30d后刚进入吸湿平台,尚未完全达到吸湿平衡;受纤维吸湿的影响;芳纶复合材料的吸湿曲线在经过初期的线性段后,迅速进入平台阶段,且试件越短,越易达到平衡。芳纶复合材料各相均具有很强的吸湿性,其吸湿行为表现为各向异性,纤维轴向的扩散系数较高,试件越短,暴露的纤维终端越多,吸湿速度就越快。
对无限大平板,水分沿材料厚度方向的表观一维扩散系数

式中:h为试样厚度;M∞为平衡吸湿含量;M(t)为时刻t的吸湿量[1、11]。
复合材料湿扩散行为属于三维扩散。设单向板长度、宽度、厚度分别为l,w,h,三个方向上的扩散系数分别为D1,D2,D3,其中方向1沿纤维向,方向2、3垂直于纤维轴向,修正边界效应后三维扩散系数与表观一维扩散系数的关系可表示为

当D2=D3时,式(22)可变为

h,w不变,改变l的值,由最小二乘法可得D1,D2。
温度80℃时,单向板吸湿实验由式(23)求得的扩散系数实验值,以及分别由混合率公式与等参化FVDAM由组分扩散系数求得的单向板扩散系数计算值见表2。其中基体的扩散系数由式(19)求得,纤维的扩散系数采用圆柱模型求解[12]。
由表2可知:纤维的扩散系数高于基体,在APMOC纤维芳香结构PPTA中,含有酰胺基,而在其第三单体CBM中又含有杂氮原子,使其吸湿性很高。由于纤维吸湿,复合材料扩散系数将明显高于将纤维视作不吸湿材料时的计算值,故不能采用Shen-Springer等简化方法求解。另外,轴向扩散系数实验值高于理论值,这主要是因为理论计算时并未考虑界面的作用,实际由于界面出现脱黏,在毛细管作用下水分将大量沿界面扩散。

表2 实验值与计算值Tab.2 Results obtained by experiment and calculation
4 结束语
本文对一种计算复合材料湿扩散系数的等参化FVDAM模型进行了研究。以界面平均相对湿浓度为基本未知量,用界面相对湿浓度连续、湿流通量连续,以及扩散方程建立用于复合材料湿扩散系数求解的等参化FVDAM模型。结果发现:等参化FVDAM模型能反映复合材料复杂微结构及纤维自身吸湿特征,较Shen-Springer,Hashin,Piggott模型更适于求解复合材料湿扩散系数,在模型中将有关湿扩散的性能参数替换为与热传导相关的性能参数即可求得宏观热传导系数。芳纶复合材料中,由于芳纶纤维本身有很大的吸湿性,由简化模型求得的结果将明显低于实验值。
[1] SHEN C H,SPRINGER G.S.Moisture absorption and desorption of composite materials[J].Journal of Composite Materials,1976(10):2-20.
[2] LI R B.Moisture absorption and hydrothermal aging in a Bismaleimode resin and its carbon fiber composite[D].Ann Arbor:University of Michigan,2001.
[3] TANG X D. Micromechanics of two-dimensional woven composites[D].College Station:Texas A &M University,2001.
[4] TANG X D.Micromechanics of moisture diffusion in composites with impermeable fibers[J].Journal of Composite Materials,2001,36:1093-1101.
[5] VADDADI P.Inverse analysis for transient moisture diffusion through fiber-reinforced composites[J].Acta Material,2003,51:177-193.
[6] ABOUDI J.Micromechanical analysis of composites by the generalized cells model[J].Mechanics of Materials,1992,14(2):127-139.
[7] ABOUDI J,PINDERA M J.Higher-order theory for periodic multiphase materials with inelastic phases[J].International Journal of Plasticity,2003,19:805-847.
[8] BANSAL Y,PINDERA M J.Finite-volume direct averaging micromechanics of heterogeneous materials with elastic-plastic phases[J].International Journal of Plasticity,2006,22:775-825.
[9] CAVALCANTE M A A,MARQUES S P C,PINDERA M J.Parametric formulation of the finite-volume theory for functionally graded materials[J].Journal of applied mechanics,2007,74(5):935-945.
[10] KHATAM H,PINDERA M J.Parametric finitevolume micromechanics of periodic materials with elastoplastic phases[J].International Journal of Plasticity,2009,25:1386-1411.
[11] ARONHIME M T.The anisotropic diffusion of water in Kevlar-epoxy composites[J].Journal of materials of science,1987,22:2435-2446.
[12] 阳建红,董进辉,李海斌.F-12纤维的吸湿行为[J].复合材料学报,2009,26(3):84-88.
